Open Problems on Information and Feedback Controlled Systems
Abstract
:1. Introduction
2. State-of-the-Art
2.1. Maxwell’s Demon
2.2. Information-Theoretic Limits of Control
2.3. Feedback Controlled Ratchets and Information
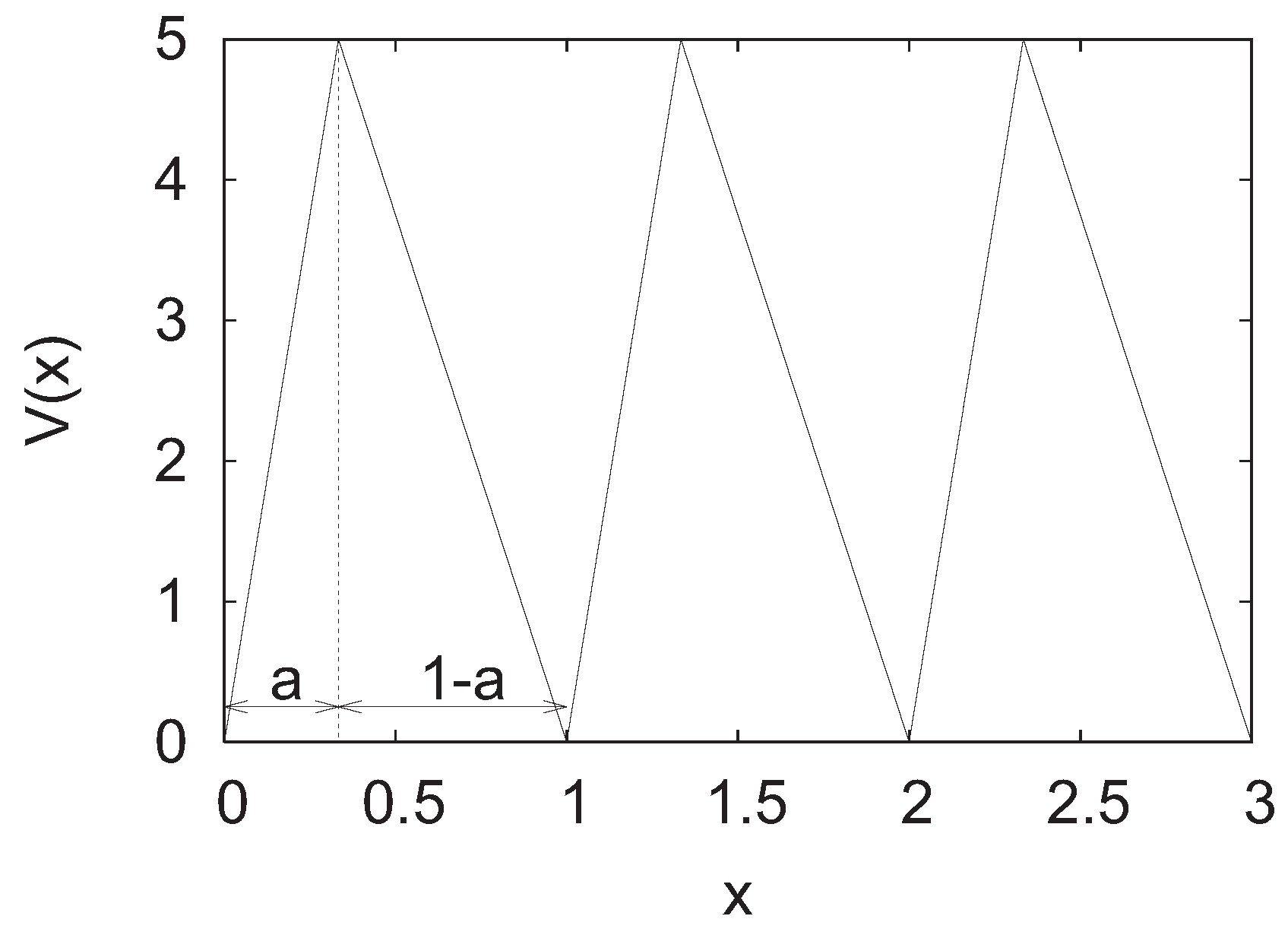
2.4. Thermodynamics of Feedback Controlled Systems
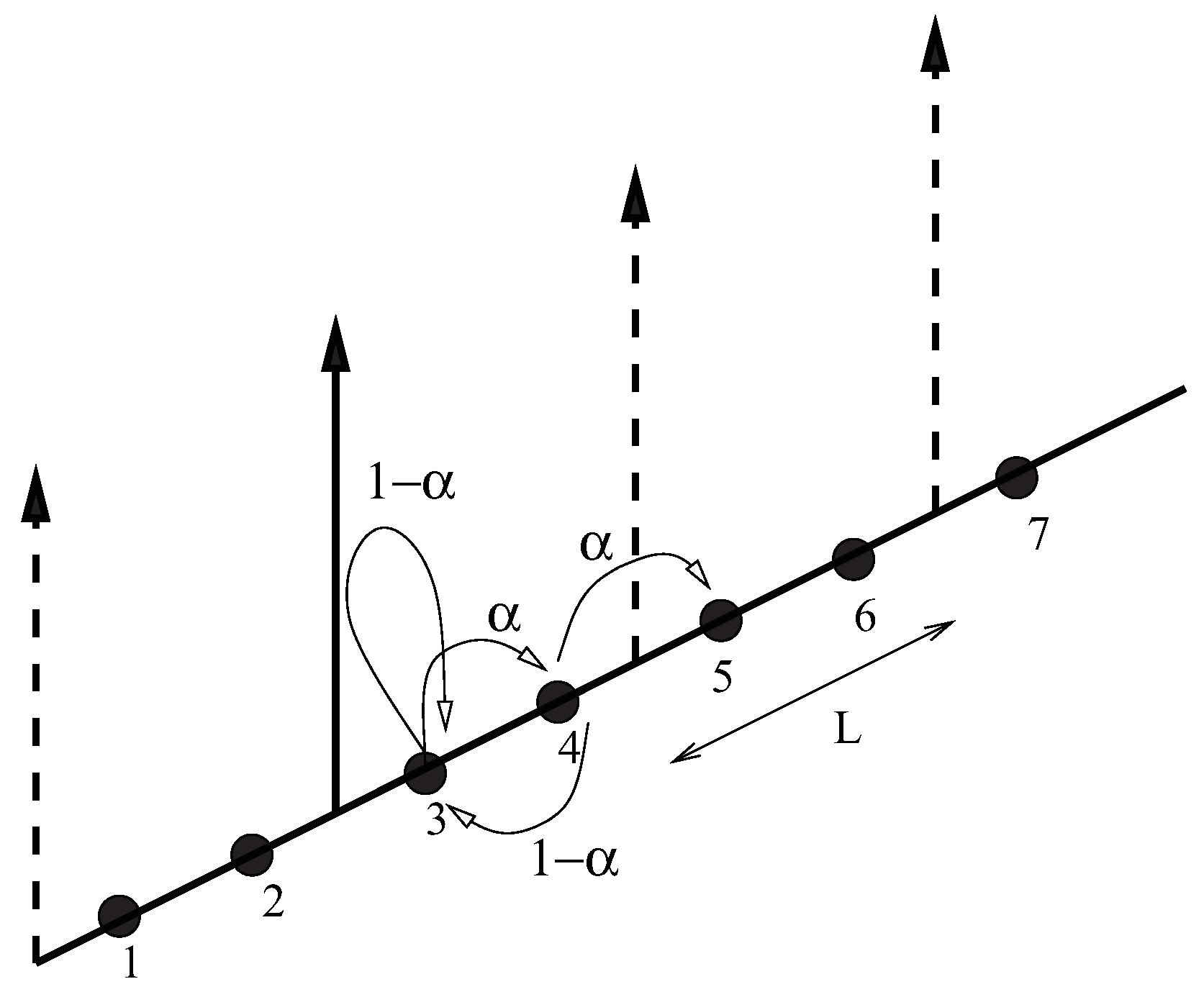
2.5. Generalization of Identities and Relations to Feedback Controlled Systems
3. Open Problems
3.1. Feedback Controlled Systems: Limitations to the Performance and Thermodynamics
3.1.1. Correlated Repeated Actuation of the Feedback Controller
3.1.2. Continuous Actuation of the Feedback Controller
3.2. Feedback Controlled Flashing Ratchets: Limitations to the Performance and Thermodynamics
3.3. Limitations to the Operation of Nanotechnology Devices and Biological Systems
4. Conclusions
Acknowledgments
References
- Bechhoefer, J. Feedback for physicist: A tutorial essay on control. Rev. Mod. Phys. 2005, 77, 783–836. [Google Scholar] [CrossRef]
- Leff, H.S.; Rex, A.F. Maxwell’s Demon 2: Entropy, Classical and Quantum Information, Computing; Institute of Physics: Bristol, UK, 2003. [Google Scholar]
- Szilard, L. On the decrease of entropy in a thermodynamic state by the intervention of intelligent beings. Z. Phys. 1929, 53, 840–856. [Google Scholar] [CrossRef]
- Landauer, R. Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 1961, 5, 183–191. [Google Scholar] [CrossRef]
- Bennett, C.H. The thermodynamics of computation—A review. Int. J. Theor. Phys. 1982, 21, 905–940. [Google Scholar] [CrossRef]
- Zurek, W.H. Algorithmic randomness and physical entropy. Phys. Rev. A 1989, 40, 4731–4751. [Google Scholar] [CrossRef] [PubMed]
- Zurek, W.H. Thermodynamic cost of computation, algorithmic complexity and the information metric. Nature 1989, 341, 119–124. [Google Scholar] [CrossRef]
- Bennett, C.H. Logical reversibility of computation. IBM J. Res. Dev. 1973, 17, 525–532. [Google Scholar] [CrossRef]
- Lloyd, S. Use of mutual information to decrease entropy: Implications for the second law of thermodynamics. Phys. Rev. A 1989, 39, 5378–5386. [Google Scholar] [CrossRef] [PubMed]
- Touchette, H.; Lloyd, S. Information-theoretic limits of control. Phys. Rev. Lett. 2000, 84, 1156–1159. [Google Scholar] [CrossRef] [PubMed]
- Touchette, H.; Lloyd, S. Information-theoretic approach to the study of control systems. Physica A 2004, 331, 140–172. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley: New York, NY, USA, 1991. [Google Scholar]
- Cao, F.J.; Feito, M. Thermodynamics of feedback controlled systems. Phys. Rev. E 2009, 79, 041118. [Google Scholar] [CrossRef]
- Lestas, I.; Vinnicombe, G.; Paulsson, J. Fundamental limits on the suppression of molecular fluctuations. Nature 2010, 467, 174–178. [Google Scholar] [CrossRef] [PubMed]
- Cao, F.J.; Dinis, L.; Parrondo, J.M.R. Feedback control in a collective flashing ratchet. Phys. Rev. Lett. 2004, 93, 040603. [Google Scholar] [CrossRef] [PubMed]
- Dinis, L.; Parrondo, J.M.R; Cao, F.J. Closed-loop control strategy with improved current for a flashing ratchet. Europhys. Lett. 2005, 71, 536–541. [Google Scholar] [CrossRef]
- Feito, M.; Cao, F.J. Threshold feedback control for a collective flashing ratchet: Threshold dependence. Phys. Rev. E 2006, 74, 041109. [Google Scholar] [CrossRef]
- Feito, M.; Cao, F.J. Time-delayed feedback control of a flashing ratchet. Phys. Rev. E 2007, 76, 061113. [Google Scholar] [CrossRef]
- Feito, M.; Cao, F.J. Transport reversal in a delayed feedback ratchet. Physica A 2008, 387, 4553–4559. [Google Scholar] [CrossRef]
- Feito, M.; Cao, F.J. Optimal operation of feedback flashing ratchets. J. Stat. Mech. Theor. Exp. 2009, P01031. [Google Scholar] [CrossRef]
- Feito, M. Feedback Brownian ratchets and information. Ph.D. Thesis, Editorial Universidad Complutense de Madrid, Madrid, Spain, 2009. Available online: http://eprints.ucm.es/10680/1/T31799.pdf (accessed on 28 March 2012). [Google Scholar]
- Craig, E.M.; Kuwada, N.J.; Lopez, B.J.; Linke, H. Feedback control in flashing ratchets. Ann. Phys. 2008, 17, 115–129. [Google Scholar] [CrossRef]
- Craig, E.M.; Long, B.R.; Parrondo, J.M.R.; Linke, H. Effect of time delay on feedback control of a flashing ratchet. Europhys. Lett. 2008, 81, 10002. [Google Scholar] [CrossRef]
- Gao, T.; Chen, J. The current transport characteristics of a delayed feedback ratchet in a double-well potential. J. Phys. A: Math. Theor. 2009, 42, 065002. [Google Scholar] [CrossRef]
- Gao, T.-F.; Liu, F.-S.; Chen, J.-C. Feedback control in a coupled Brownian ratchet. Chin. Phys. B 2012, 21, 020502. [Google Scholar] [CrossRef]
- Son, W.-S.; Ryu, J.-W.; Hwang, D.-U.; Lee, S.-Y.; Park, Y.-J.; Kim, C.-M. Transport control in a deterministic ratchet system. Phys. Rev. E 2008, 77, 066213. [Google Scholar] [CrossRef]
- Hennig, D.; Schimansky-Geier, L.; Hänggi, P. Directed transport of an inertial particle in a washboard potential induced by delayed feedback. Phys. Rev. E 2009, 79, 041117. [Google Scholar] [CrossRef]
- Hennig, D. Current control in a tilted washboard potential via time-delayed feedback. Phys. Rev. E 2009, 79, 041114. [Google Scholar] [CrossRef]
- Zhang, X.-M.; Ai, B.-Q. Transport of overdamped Brownian particles driven by ac forces and time-delayed feedback. J. Phys. A: Math. Theor. 2010, 43, 495004. [Google Scholar] [CrossRef]
- Du, L.-C.; Mei, D.-C. Time delay control of absolute negative mobility and multiple current reversals in an inertial Brownian motor. J. Stat. Mech. Theor. Exp. 2011, 2011, P11016. [Google Scholar] [CrossRef]
- Lopez, B.J.; Kuwada, N.J.; Craig, E.M.; Long, B.R.; Linke, H. Realization of a Feedback Controlled Flashing Ratchet. Phys. Rev. Lett. 2008, 101, 220601. [Google Scholar] [CrossRef] [PubMed]
- Astumian, R.D.; Derényi, I. Fluctuation driven transport and models of molecular motors and pumps. Eur. Biophys. J. 1998, 27, 474–489. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.-X.; Chen, Y.-D. Chemically Driven Motility of Brownian Particles. Phys. Rev. Lett. 1996, 77, 194–197. [Google Scholar] [CrossRef] [PubMed]
- Bier, M. The Stepping Motor Protein as a Feedback Control Ratchet. Biosystems 2007, 88, 301–307. [Google Scholar] [CrossRef] [PubMed]
- Serreli, V.; Lee, C.-F.; Ray, E.R.; Leigh, D. A molecular information ratchet. Nature 2007, 445, 523–527. [Google Scholar] [CrossRef] [PubMed]
- Feynman, R.P.; Leighton, R.B.; Sands, M. The Feynman Lectures on Physics I; Addison-Wesley: Reading, MA, USA, 1963; Chapter 46. [Google Scholar]
- Van den Broeck, C.; Meurs, P.; Kawai, R. From Maxwell demon to Brownian motor. New J. Phys. 2005, 7, 10. [Google Scholar] [CrossRef]
- Cao, F.J.; Feito, M.; Touchette, H. Information and flux in a feedback controlled Brownian ratchet. Physica A 2007, 388, 113–119. [Google Scholar] [CrossRef]
- Feito, M.; Cao, F.J. Information and maximum power in a feedback controlled Brownian ratchet. Eur. Phys. J. B 2007, 59, 63–68. [Google Scholar] [CrossRef]
- Allahverdyan, A.E.; Saakian, D.B. Thermodynamics of adiabatic feedback control. Europhys. Lett. 2008, 81, 30003. [Google Scholar] [CrossRef]
- Toyabe, S.; Sagawa, T.; Ueda, M.; Muneyeki, E.; Sano, M. Experimental demonstration of information-to-energy conversion and validation of the generalized Jarzynski equality. Nature Phys. 2010, 6, 988–992. [Google Scholar] [CrossRef]
- Abreu, D.; Seifert, U. Extracting work from a single heat bath through feedback. Europhys. Lett. 2011, 94, 10001. [Google Scholar] [CrossRef]
- Horowitz, J.M.; Parrondo, J.M.R. Thermodynamic reversibility in feedback processes. Europhys. Lett. 2011, 95, 10005. [Google Scholar] [CrossRef]
- Vaikuntanathan, S.; Jarzynski, C. Modeling Maxwells demon with a microcanonical Szilard engine. Phys. Rev. E 2011, 83, 061120. [Google Scholar] [CrossRef]
- Abreu, D.; Seifert, U. Thermodynamics of genuine nonequilibrium states under feedback control. Phys. Rev. Lett. 2012, 108, 030601. [Google Scholar] [CrossRef] [PubMed]
- Sagawa, T.; Ueda, M. Nonequilibrium thermodynamics of feedback control. Phys. Rev. E 2012, 85, 021104. [Google Scholar] [CrossRef]
- Sagawa, T.; Ueda, M. Generalized Jarzynski equality under nonequilibrium feedback control. Phys. Rev. Lett. 2010, 104, 090602. [Google Scholar] [CrossRef] [PubMed]
- Sagawa, T. Hamiltonian derivations of the generalized Jarzynski equalities under feedback Ccontrol. J. Phys. Conf. Ser. 2011, 297, 012015. [Google Scholar] [CrossRef]
- Sagawa, T. Thermodynamics of information processing in small systems. Prog. Theor. Phys. 2012, 127, 1–56. [Google Scholar] [CrossRef]
- Jarzynski, C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 1997, 78, 2690–2693. [Google Scholar] [CrossRef]
- Horowitz, J.M.; Vaikuntanathan, S. Nonequilibrium detailed fluctuation theorem for repeated discrete feedback. Phys. Rev. E 2010, 82, 061120. [Google Scholar] [CrossRef]
- Ponmurugan, M. Generalized detailed fluctuation theorem under nonequilibrium feedback control. Phys. Rev. E 2010, 82, 031129. [Google Scholar] [CrossRef]
- Lahiri, S.; Rana, S.; Jayannavar, A.M. Fluctuation theorems in the presence of information gain and feedback. J. Phys. A: Math. Theor. 2012, 45, 065002. [Google Scholar] [CrossRef]
- Mitter, S.K.; Newton, N.J. Information and entropy flow in the KalmanBucy filter. J. Stat. Phys. 2005, 118, 145–176. [Google Scholar] [CrossRef]
- Sandberg, H.; Delvenne, J.-C.; Doyle, J.C. Linear-Quadratic-Gaussian heat engines. In Proceedings of the 46th IEEE Conference on Dec. and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 3102–3107.
- Stengel, R.F. Optimal Control and Estimation; Dover Publications: New York, NY, USA, 1994. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Cao, F.J.; Feito, M. Open Problems on Information and Feedback Controlled Systems. Entropy 2012, 14, 834-847. https://doi.org/10.3390/e14040834
Cao FJ, Feito M. Open Problems on Information and Feedback Controlled Systems. Entropy. 2012; 14(4):834-847. https://doi.org/10.3390/e14040834
Chicago/Turabian StyleCao, Francisco J., and Manuel Feito. 2012. "Open Problems on Information and Feedback Controlled Systems" Entropy 14, no. 4: 834-847. https://doi.org/10.3390/e14040834



