1. Introduction
A large number of theoretical models and experiments, purporting to represent real systems in thermodynamic equilibrium, have been published in which exotic thermodynamic behavior is found, such as negative susceptibilities (e.g., negative heat capacity), or violation of thermodynamic law. These results are usually obtained in small systems with long-range forces, i.e., long with respect to the physical size of the system. Examples are; gravitational systems [
1,
2], nanoclusters [
3,
4,
5,
6,
7], heavy ion fragmentation [
8,
9], spin systems [
10], magnetically self-confined plasma [
11], and general models [
12]. Other works have gone even further to claim violation of fundamental thermodynamic law for such model systems [
13]. In light of these persistent and disconcerting claims, it is prudent to review the statistical mechanical foundation of equilibrium thermodynamic formalism in order to examine the validity of applying such a formalism on these systems. It is, of course, well known that applying equilibrium thermodynamic formalism to systems which are not in thermodynamic equilibrium, or which in principle cannot reach thermodynamic equilibrium, will result in inconsistencies in the analysis [
14].
Equilibrium thermodynamic formalism is derivable from statistical mechanics only under the fundamental axioms of statistical independence and a priori equal probability of the microstates. These conditions place restrictions on the dependence of the number of microstates
on the extensive variables
for the system. In particular, we show here that the variation in the number of microstates with any one of the extensive variables
X is limited by the inequality
where
and
, and that model systems not respecting this criterion violate independence or equal probability of the microstates and do not have an extremum-maximum with respect to partition of the extensive variable
X and thus should not be assumed to be treatable under equilibrium thermodynamic formalism. Such models are not representative of real system in nature. Inconsistencies will result when such models are treated under equilibrium thermodynamic formalism. These inconsistencies should not be considered as exotic new physics or violation of fundamental law, but rather as inconsistencies arising from the unjustified application of the equilibrium thermodynamic formalism to the model system.
There are a number of ways in which to construct models which do not satisfy our criterion (
1) on
which is the criterion that guarantees an extremum maximum. Nature, however, is constrained by quantum mechanics and the fundamental symmetries and constants in its system building. The existence of pure quantum states and quantum tunneling resulting from interactions with the quantum vacuum, means that natural systems respect a priori the equilibrium thermodynamic axioms of microstate independence and equal probability. Natural systems also respect the fundamental symmetries and constants of nature. One such fundamental constant, leading to the quantization of natural systems, is Planck’s constant,
h. We show here that, in the absence of infinite-range forces, quantization endows natural systems with a number of microstates dependence on the extensive variables,
, which is a scale invariant power law. All power law relations for
satisfy the above criterion on
. Such natural systems can therefore, in the isolated regime and in the sufficiently time relaxed limit, always be treated consistently with equilibrium thermodynamic formalism.
In the following section we discuss the statistical mechanical foundation of equilibrium thermodynamic formalism and derive the above mentioned criterion (
1) of the dependence of the number of microstates
on the extensive variables. In
Section 3 we describe how this criterion negates the possibility of negative heat capacity and convex intruders in the entropy function for systems in thermodynamic equilibrium.
Section 4 shows how the criterion on
may also be violated, even for physically consistent models or real systems, if
is determined through non-ergodic means. Such a violation, whatever the origin, also leads to in-equivalence of results obtained in the microcanonical and canonical ensembles.
Section 5 demonstrates that natural quantum systems, in the absence of infinite-range forces, obey a priori the criterion on
and thus can, in principle, reach thermodynamic equilibrium. Specific examples of model design leading to systems which cannot atain thermodynamic equilibrium and therefore resulting in inconsistencies in the thermodynamic analysis are given in
Section 6. Conclusions are presented in
Section 7.
2. Equilibrium: An Extremum-Maximum in the Number of Microstates
Consider an isolated system with fixed extensive variables; total energy
E, volume
V, particle number
and any other extensive variable (specified by “...”). Assume that the system is composed of two subsystems, 1 and 2, and that each subsystem may have a different equation of state (different dependencies of the number of microstates on the extensive variables) as specified by
and
, but each subsystem individually is time relaxed and spatially homogeneous. Assume that between subsystems there are fixed walls impermeable to the exchange of all extensive variables except one,
X, for example the energy
E, which is free to be exchanged between the two subsystems. Assuming independence of the microstates, the total number of microstates available to the combined system is,
where
The further assumption of
a priori equal probability of the microstates then implies that the time evolved, most probable macrostate of the isolated system, named the equilibrium state, is that macrostate specified by the particular partition of the energy between subsystems which has the largest number of microstates consistent with the all constraints. To determine the most probable partition of the total fixed energy
we first consider the contribution to the total number of microstates for a particular energy partition “
p” with definite values for
and
,
and look for an extremum-maximum of this function with respect to variation of
or
with
E fixed. For example, in terms of
the extremum is determined by,
It is easy to verify that this leads to the condition [
15]
where, for brevity, we have suppressed the dependence on the other, assumed constrained, extensive variables. The connection of statistical mechanics with phenomenological thermodynamic formalism is made by assigning the entropy of both subsystems as [
14]
and thus the condition defining the extremum, Equation (
5), becomes
implying equal temperatures of the two subsystems for the partition of the total energy corresponding to an extremum.
If the extremum in
corresponds to a maximum, then in the time relaxed equilibrium state, the total energy
E will thus be partitioned among the subsystems such that the resulting equilibrium macrostate, with definite values of
and
will be the most probable, that corresponding to the largest number of microstates, and this will be the partition giving equal temperatures. Likewise, the equilibrium partition of the volume, or of the number of particles, with the other extensive variables constrained by impermeable walls, is that which equalizes the pressure over temperature,
, or the chemical potential over temperature,
, respectively over the subsystems [
15].
Therefore, statistical mechanics, under the assumptions of independence and equal probability of the microstates, explains the phenomenological equilibrium state as that macrostate, among all possible macrostates, with the maximum number of microstates consistent with all constraints. The question then arises: Does an extremum-maximum in the number of microstates, with respect to partition of an unconstrained extensive variable, always exist for whatever dependency of on the extensive variable?
We will now show that the general answer to this question is no, and thus not all model systems can attain, even in principle, thermodynamic equilibrium. The criterion (
1), to be derived below, on the functional form of the dependence of
on the extensive variables, can thus be used to discriminate between models which can in time relax to a thermodynamic equilibrium, and models which cannot, even in principle.
The Extremum-Maximum Condition
We have tacitly assumed that the extremum as given by (
4) or (
5) corresponds to a maximum in the number of microstates. This, however, must be verified for whatever system by determining the curvature of
evaluated at its extremum, i.e., the sign of the second derivative of the contribution to the total number of microstates of a particular partition,
with respect to the unconstrained extensive variable
. For the extremum to correspond to a maximum it is thus required that (using Equation (
4) and that
),
where
X represents any extensive variable which is unconstrained, and where
,
and their derivatives, are to be evaluated at the extremum.
Consider now the particular case that the two independently homogeneous subsystems are identical. Since at the extremum the intensive variable, corresponding to the unconstrained extensive variable
(or
), is homogeneous (see, for example, Equation (
7)) we must necessarily have that
,
,
, etc., where each is to be evaluated at the extremum. The extremum-maximum condition (
8) then becomes
or, in general (dropping the subscripts), giving that
where
and
. Equation (
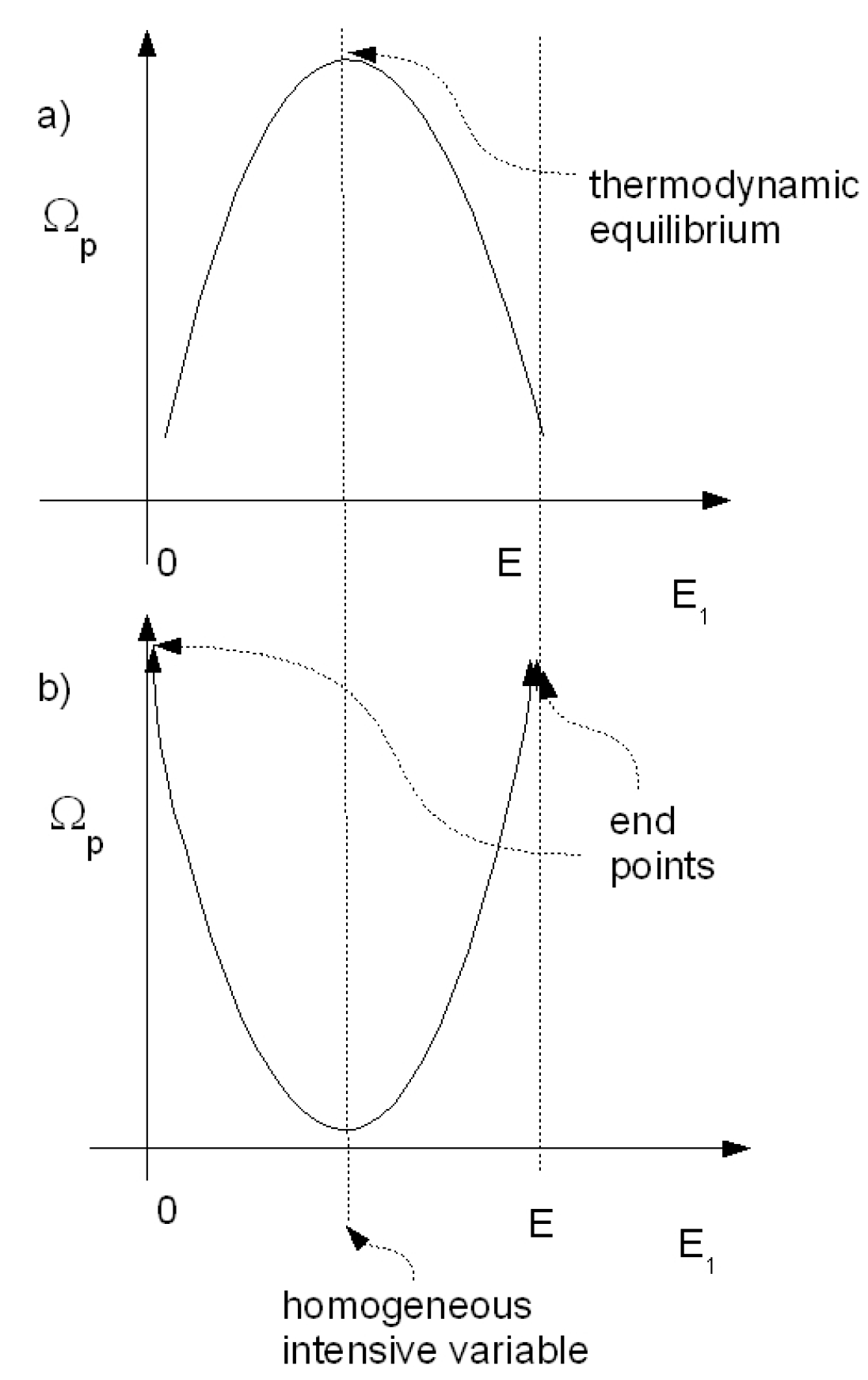
9) is thus a very general criterion that must be satisfied for the number of microstates dependence on any one of the extensive variables if the model is to be representative of a physically consistent system that has an extremum-maximum and can thus reach thermodynamic equilibrium (see
Figure 1a).
For example, while a power law dependence of the form
, for some positive constant
, satisfies condition (
9) for the exponent
, an exponential dependence,
, only satisfies condition (
9) if
If
,
, and thus no extremum exists. If
, then the extremum of (
3) is a minimum,
not a maximum, i.e.,
(see
Figure 1b). Functions of sums of two power laws (for example
), with the powers greater than zero but different, can also fail to satisfy (
9) near the energy
. This latter case is directly related to the erroneous determination of negative heat capacity for nanoclusters [
16], which are often trapped in the microcanonical ensemble (see below and [
17]).
In summary, models which purport to represent real systems which can arrive at thermodynamic equilibrium, but which have a number of microstates (or phase space volume) dependence on any one of the extensive variables which does not satisfy criterion (
9), can never reach thermodynamic equilibrium, simply because no macrostate for the system exists that corresponds to an extremum-maximum in the number of microstates. The extremum, if it exists, is a minimum (see
Figure 1b), and thus homogeneity of the intensive variables, e.g., temperature, pressure, or chemical potential, are the
least likely macrostates, and therefore are not synonymous with thermodynamic equilibrium. These models may have a maximum in the number of microstates, but it is not an extremum, it corresponds to the end points where all of the unconstrained extensive variable will be found in one singular part of the system, leading to in-homogeneous intensive variables. For classical continuous model systems, this, in fact, would correspond to a singularity in the unconstrained extensive variable at some point in the volume (analogous to a black hole). This would only apply to model systems since, as we show in this article, real systems are subject to a finite Planck’s constant and this always endows them with a density of states respecting the equilibrium criterion and real systems are therefore free of such singularities.
Note that for classical isolated small systems with long-range forces (with respect to the size of the system), the factorization of the microstates, Equation (
2), will in general not apply, and the total number of microstates of the combined system cannot be obtained by simple decomposition of the system into subsystems. However, in this case, the very notion of subsystems and constraints becomes unworkable. In fact, it makes little sense to speak of the volume or the energy distribution over such a system. The system will in general time relax to a trapped, reduced, sub-space of the allowed phase space, the particular region being dependent on the initial conditions. The system cannot be considered to be in equilibrium and therefore equilibrium thermodynamic formalism simply does not apply. If one insists on using the entropy such as the Gibbs entropy
or the Boltzmann entropy
(obtained from the Gibbs entropy by assigning equal probability to each microstate
) then one will frequently arrive at inconsistencies such as negative heat capacity or violations of established fundamental laws since raising the energy may un-trap the system and allow it to reach previously inaccessible regions of phase space [
17].
Small classical systems with long range forces treated in the canonical ensemble, however, can, in principle, be treated with equilibrium thermodynamic formalism since in this case energy can be obtained from the heat bath to avoid permanent trapping and the system will eventually visit all of allowed phase space. However, the crucial point here is the word “eventually” since barriers in energy or angular momentum, etc., may be so high that true thermodynamic averages become impractical for lack of time. The analysis is non-ergodic. This is the case, for example, when bimodal energy distributions are found [
4]. For a system considered in the canonical ensemble, our criterion (
9) still applies but now the microstates are of the system plus heat bath.
In reality, truly isolated systems do not exist in Nature. All material exists in a world in which the system is immersed in the quantum vacuum, which can be thought of as providing a canonical ensemble since an extensive variable can be borrowed from the vacuum to overcome barriers as long as the uncertainty principle is respected (providing for quantum tunneling, for example). As long as the forces are not of exactly infinite range, any real system therefore can in principle attain thermodynamic equilibrium. The distribution of the measured number of microstates with any of the extensive variables for real systems must satisfy our criterion (
9).
3. Negative Heat Capacity and Convex Intruders
Using the thermodynamic definitions of the entropy,
the temperature
, and the heat capacity
, it is straight forward to show that the heat capacity in terms of the number of microstates and its variation in energy is,
From this relation, it is obvious that if the heat capacity of a model system is to become negative, it is required that
, but this contradicts exactly the extremum-maximum condition required for a stable thermodynamic equilibrium, our criterion (
9). Therefore, any system displaying negative heat capacity cannot simultaneously be in thermodynamic equilibrium.
Furthermore, it is also evident from (
10) that if the heat capacity of a system is to change from being positive to being negative at some energy, then it must first go through positive infinity, then flip to negative infinity, which is obviously not phenomenological.
Assuming the Boltzmann relation
the entropy function will show a convex intruder if
giving that
, which, again, is in direct contradiction to the criterion required for thermodynamic equilibrium. Therefore, any system showing a convex intruder in the entropy function (or, equivalently, a concave intruder in the energy function) cannot simultaneously be in thermodynamic equilibrium.
4. Ergodicity and In-Equivalence of Ensembles
Negative heat capacity and convex intruders may result even when employing models which are physically consistent with the equilibrium axioms but when using simulations to determine
which are not ergodic, leading to a determined
which does not satisfy criterion (
9). Long-range forces in small systems lead to large energy barriers separating different regions of the energetically available phase space. For classical simulations, independence and a priori equal probability of the microstates cannot be assumed if there is not sufficient energy available in the system to surmount the barriers. This occurs frequently below the solid to liquid transition energy in small nanoclusters when treated in the classical microcanonical ensemble [
17].
The determined
from these simulations may not satisfy the extremum-maximum criterion (
9) (even though an ergodically determined
will) since on surmounting an energy barrier, suddenly (in energy) a large portion of previously inaccessible phase space becomes available. The measured energy dependence of
may thus increase arbitrarily rapidly with energy, violating criterion (
9) and leading to the erroneous determination of negative heat capacity. The problem is not easy to identify beforehand as it is related to the particularly difficult task of proving the ergodicity of a dynamical system.
This, however, is not an “in principle” problem for simulations in the canonical ensemble since any amount of energy can be obtained from the heat bath for surmounting whatever barrier. This assumes, however, that sufficient time is allowed for the trajectory to visit all allowed microstates. If not, bi-modal energy distributions at a fixed temperature may be found [
17]. The Laplace transform between the ensembles is not valid for these non-ergodic simulations. This is the origin of the in-equivalence of the canonical and microcanonical ensembles for such simulations.
In the case of convex intruders, the thermodynamically stable states correspond to points on the tangent lines lying everywhere above the entropy function [
14]. Taking these tangent lines to define the stable states is equivalent to ignoring the barriers and imposing equal probability to all of the microstates, including the mixed solid-liquid states energetically available but not accessible because of high energy barriers [
17].
Taking the determined entropy function with a convex intruder, obtained from a non-ergodic simulation, as the fundamental relation, will result in inconsistencies in the equilibrium thermodynamic formalism (see also [
17,
18,
19,
20]).
5. Natural Quantum Systems
We now show that natural quantum systems, in the absence of infinite-range forces, obey the equilibrium thermodynamic axioms of independence and equal probability of the microstates and, as a peculiarity of quantization, have a number of microstates dependence that satisfies condition (
9) at all values of the extensive variable.
Non-ergodicity, or trapping by barriers, is not an “in principle” problem in quantum systems because of quantum tunneling resulting from the interaction of the system with the quantum vacuum. The principle of detailed balance, resulting from the time reversibility of the Schrödinger equation, then ensures that all microstates have a priori equal probability [
14].
The existence of a finite Planck’s constant implies that the energy, volume, particle number, and any other extensive variable, eigenstates are quantized. Consider, for example, a state space of a simple system of fixed energy
volume
V, and particle number
containing
D degrees of freedom for storing energy. Assume that the energy is quantized in units of
(for example, the Einstein model of a solid [
14], where
, with
N equal to the number of particles). The number of microstates available to this system corresponds to the number of ways to distribute the
energy packets over
D degrees of freedom, which is [
14]
where the result to the right of the “≈” sign is obtained by calculating the number of quantum states with energy less than, or equal to,
which is a very good approximation for the number of microstates
with energy between
E and
as long as
[
14]. The number of microstates of a quantum system thus increases as a scale invariant power law in energy
with the exponent of the power law being equal to the number of independent degrees of freedom
D. This result does not depend on whether the frequencies of all modes are the same,
or whether there exists a spectrum of frequencies
.
A similar power law can be obtained for the number of microstates dependence on the other extensive variables, such as the volume
or the particle number
N. For example, the dependence of
on the number of particles
N can be found by holding constant the total energy and allowing
N to vary. By the inherent symmetry apparent in the term to the left of the “≈” sign in Equation (
11), and for
it is easy to see that the result is
It is trivial to show that all power law relations satisfy criterion (
9). Therefore, all natural (quantum) systems in the absence of infinite-range forces can, in principle, attain stable thermodynamic equilibrium.
In the limit
, the exponent of the power law
(see Equation (
12)), and it is easy to verify that in this case
and thus, in this limit, there exists no extremum-maximum, no thermodynamic equilibrium. Quantization of the energy, or the existence of a finite Planck’s constant, is therefore a necessary condition to ensure thermodynamic stability of an isolated macroscopic system. The same holds true for quantization of particle number, volume, and spin, etc. This is the macroscopic analogue of the fact that quantization is a necessary condition to ensure the stability of the atom.
6. Non-Physical Model Design
Models meant to provide insight into the thermodynamic behavior of natural systems must have incorporated in their construction all the degrees of freedom and their correspondent constraints that the real system is subject to in nature. For example, models representing isolated systems must respect conservation of energy, momentum, angular momentum, volume, charge, particle number, etc. However, there are other constraints that arise because of the fundamental constants of Nature. For example, maximum signal rates (velocity of interaction) cannot exceed the velocity of light,
c. Also, the number of microstates within a given volume
of state space cannot exceed the value
[
14], where
D is the dimension of the state space, which is limited by the finite value of Planck’s constant
This requirement is equivalent to the quantization of thermodynamic variables, including those arising from internal degrees of freedom, such as spin. Furthermore, quantum tunneling resulting from interaction with the vacuum, plus the reversibility of the Schrödinger equation, then ensures equal probability of the microstates [
14]. In counting microstates, it is also important to take into account the indistinguishable nature of elementary particles and their particular statistics (Fermi–Dirac, or Bose–Einstein). Although at high temperatures or low pressures, the quantum description often coincides with the classical description for some thermodynamic properties, this is not the case for counting microstates, as the Gibb’s paradox reveals [
14].
Relevant models must also be physically consistent. For example, internal interaction fields providing an exchange of energy cannot be presumed to exist in isolation, but must necessarily arise from internal material sources. External fields affecting the internal energy or entropy, must be taken into account by, for example, modifying the chemical potentials [
21].
Still another important condition for the thermodynamic analysis to be free of inconsistencies is that the number of extensive variables used in the analysis must be commensurate with the number of degrees of freedom in the models state space, which depends on the particular Hamiltonian of the system [
14,
22]. For example, inconsistencies in the thermodynamic modeling of molecular hydrogen gas led to the discovery of ortho- and para-hydrogen [
14].
Models not respecting the fundamental axioms or the requirements of consistent model building presented above will present inconsistencies when treated under equilibrium thermodynamic formalism which was constructed on the basis of the existence of these axioms and consistency [
14]. In this paper we have shown that the most general criterion for the existence of a extremum-maximum, and therefore the applicability of equilibrium thermodynamic formalism, is
Neglect of this consideration when constructing models has often lead to incorrectly reporting inconsistencies as if they were indicative of new physical phenomena, or of violations of fundamental thermodynamic law.
For completeness we present some published models which, by construction or through non-ergodic simulation, violate criterion (
9) for different reasons and a thermodynamic anaylsis has therefore led the authors to erroneously conclude the violation of thermodynamic stability conditions or the violation of fundamental thermodynamic law.
In [
3], a model is presented purporting to demonstrate the possibility of negative heat capacity in nanoclusters. The energies of the microstates in this model are arbitrarily assigned and not derived by resolving the Schrödinger equation with a physically consistent Hamiltonian, or by the quantization of a classical phase space volume. The model, in fact, violates the condition of energy quantization by having an arbitrarily large degeneracy in energy of the higher energy states, leading to a violation of the extremum-maximum criterion on
. Such models do not respect a finite Planck’s constant which imposes a power law distribution on the energy states, and, furthermore, the model does not respect correct particle statistics. Therefore, the model cannot be used for elucidating equilibrium thermodynamic properties of real nanoclusters.
Another model, also purporting to lend support for negative heat capacity in real systems, is given in [
2]. Here, internal fields not arising from material sources are included, and the volume is arbitrarily defined by a non-interacting sphere. The energy input into the system due to material interaction with the field should have been taken into account consistently by defining new intensive variables (e.g., new chemical potentials) [
18].
Yet another example of a model violating the criterion on
by construction and leading to the erroneous conclusion of negative heat capacity, and further suggesting violation of the zeroth law of thermodynamics, is given in [
13]. The model consists of
N rotors (spin). A kinetic energy term and an infinite-range spin-spin interaction are modeled by a Hamiltonian of form
where
J is the spin-spin coupling constant, and
the angle of the rotor with respect to a given axis. This system, in fact, has no spatial dimension so the Hamiltonian of the system does not depend on a spatial dimension. When the thermodynamic analysis of this system is carried out using an entropy function dependent on only two extensive variables, the total energy per particle and a total magnetization order parameter
m, the thermodynamic results are consistent, and the microcanonical and canonical ensemble results are equivalent [
13].
However, the authors then add a “nearest neighbor” interaction of form
to the Hamiltonian with periodic boundary conditions imposed. This implies the introduction of a new coordinate of spatial dimension. Without taking into account this new dimension in the thermodynamic analysis, nor considering the quantization of the spin nor energy states (see
Section 5), the distribution of these variables becomes non-homogeneous when the entropy is maximum, exemplifying a situation similar to that of
Figure 1b. The system does not have an extremum-maximum, but rather endpoint maxima at which all the magnetization or energy is in one part of the system. Alternation between the two most probable states can be observed with time indicating a system that can never reach thermodynamic equilibrium.
Non-ergodic experiments or simulations, although employing physically consistent models, can also lead to a determined energy dependence of
that does not respect the extremum-maximum criterion, thereby giving “apparent” negative heat capacity. Such results on nanoclusters have been frequently presented in the literature [
3,
4,
5,
6,
7,
23,
24]. The consensus, but incorrect, explanation of these results is that negative heat capacity arises from a particular, but inherent, distribution of the energy states of the nanocluster [
3,
4,
5,
24]. However, this explanation ignores the additional degrees of freedom for carrying energy that arise as the system changes phase, i.e., that the heat capacity for the liquid phase and solid phases are different, as clearly demonstrated in both experiment and simulation [
7]. It is, in fact, the hiding of these additional degrees of freedom in the microcanonical ensemble due to large energy barriers that leads to the erroneous determination of negative heat capacity [
16,
17].