Quantum Genetic Learning Control of Quantum Ensembles with Hamiltonian Uncertainties

Abstract

In this paper, a new method for controlling a quantum ensemble that its members have uncertainties in Hamiltonian parameters is designed. Based on combining the sampling-based learning control (SLC) and a new quantum genetic algorithm (QGA) method, the control of an ensemble of a two-level quantum system with Hamiltonian uncertainties is achieved. To simultaneously transfer the ensemble members to a desired state, an SLC algorithm is designed. For reducing the transfer error significantly, an optimization problem is defined. Considering the advantages of QGA and the nature of the problem, the optimization problem by using the QGA method is solved. For this purpose, $N$ samples through sampling of the uncertainty parameters via uniform distribution are generated and an augmented system is also created. By using QGA in the training step, the best control signal is obtained. To test the performance and validation of the method, the obtained control is implemented for some random selected samples. A couple of examples are simulated for investigating the proposed model. The results of the simulations indicate the effectiveness and the advantages of the proposed method.

1. Introduction

In quantum phenomena, as in the classical systems, the existence of uncertainties and noises are unavoidable. For example, in superconducting qubits, the coupling energy of a Josephson junction may have fluctuations [1,2]. Noises and fluctuations may exist in magnetic fields and electric fields in cavity quantum electrodynamics (QED) [3,4]. The spins of an ensemble in nuclear magnetic resonance (NMR) experiments may not be exactly known with respect to the strength of the applied radio frequency field [5].

The classification of inhomogeneous quantum ensembles is a significant issue which has many applications in the discrimination of atoms (or molecules), the separation of isotopic molecules, and quantum information extraction. Thus, treating the quantum systems with uncertainties is an important and applicable subject which needs to be considered.

A quantum ensemble consists of a large number of single quantum systems. In the practical world, some of the quantum systems exist in the form of quantum ensembles. Each single quantum system in a quantum ensemble is referred to as a member of the ensemble [6]. Quantum ensembles have wide applications in emerging quantum technology, including long-distance quantum communication [7], quantum computation [8], and magnetic resonance imaging [9].

Control of inhomogeneous quantum ensembles is an important issue in practical applications. Control of inhomogeneous quantum systems for discrimination between two or more similar systems, for instance, is an attractive field of study [10]. In practical applications, the members of quantum ensembles could have variations in some parameters of dynamic systems. These situations are referred to as inhomogeneous quantum ensembles [6].

There are many approaches which can be used for solving quantum control problems with uncertainties. For instance, an optimal control for NMR pulse sequences is designed by applying gradient algorithms [11]. Additionally, a sequential convex programming method is proposed for designing robust quantum manipulations [12]. Dong and his collogues have designed a development of the variable structure control approach with sliding modes to improve the robustness of quantum systems in which a sliding mode control method is presented for two-level quantum systems to treat bounded uncertainties in the system Hamiltonian [13]. In addition to these works, a Lyapunov control method is presented to attain a universal quantum control [14]. For the first time a sampling-based learning control (SLC) of inhomogeneous quantum ensembles is presented for overcoming the compensation for parameter dispersion [6]. As an important application, the sampling-based learning controller is used for designing of a superconducting quantum control of systems [15]. Construction of universal quantum gates by using a sampling-based learning control are presented in order to find robust optimal control fields in the presence of different fluctuations and uncertainties [16]. Furthermore, an extended sampling-based learning control for designing a robust quantum unitary transformation in quantum information processing is presented and implemented [17]. In other applications, to prevent a control field failing in laser-assisted collisions, a sampling-based robust control is used [18].

In [19], a systematic sampling-based learning control method with gradient-based learning algorithms for steering the components of inhomogeneous quantum ensembles with uncertainties to the same ideal state is investigated by Dong and coworkers. There are some challenges in gradient algorithms. For instance, they may fall into a local optimum depending on the initial choices of problem variables or, in complex situations, function derivatives may not be easily found.

Genetic-type algorithms (GAs) have being used in optimization problem-solving. For this purpose, by applying cross-over and mutation operators on current solutions, new solutions are generated and, statistically, they are moving toward optimal solutions in the search space. The set of solutions, however, converges to an optimum solution according to the principle of the Darwinian theory of evolution.

The quantum genetic algorithm (QGA) was identified by Narayanan and Moore [20]. The QGA, with even a smaller population, presents a great ability of global optimization and good robustness. Therefore, as compared with the common genetic algorithm, QGA has greater effectiveness [21,22]. QGAs are mostly constructed based on qubits (or quantum bits) and state superposition in quantum mechanics. In contrast to classical representations of chromosomes (a binary string, for instance), here they are represented by vectors of qubits (quantum registers).

In this paper, for controlling the quantum systems with uncertainties, a hybrid method based on the SLC method and QGA is used. Specially, artificial samples are generated by sampling the uncertainty parameters in the system model and an augmented system is constructed by using these samples in the training step. Then, to train a control law with the desired performance for the augmented system, QG (quantum genetic) learning and optimization algorithms are used. In the process of testing, a set of selected uncertainty samples is tested to evaluate the control performance. Additionally, an improvement of QGA is conducted to attain better results. In [22] an adding quantum mutation operation in the conventional quantum genetic algorithm is used as an improving device. Quantum mutation, by swapping the value of the probability amplitude of qubits (α, β), can completely reverse the individual’s evolutionary direction. In this paper the mutation operation is implemented on measured qubits (bit strings), which is more effective than adding quantum mutation. Reduction of learning iterations, test error and training error, and also increasing the fidelity index are advantages of the proposed method.

This paper is organized as follows: Section 2 represents the quantum control model and formulates the control problem; A quantum genetic learning ensemble control algorithm is designed in Section 3; Simulation results and control performance are illustrated in Section 4; Conclusions are presented in Section 5.

2. Problem Formulation

In this paper, a finite-dimensional ($N$-level) closed quantum system with a state in an underlying Hilbert space is considered. The states can be written as a superposition of eigenstates as follows:

$$|\psi \left(t\right)\rangle =\sum _{i=1}^N{c}_i\left(t\right)|{\varphi }_i\rangle$$

(1)

where complex numbers $c_i\left(t\right)$ satisfy ${\sum }_{i=1}^N{\left|c_i\left(t\right)\right|}^2=1$ and ${\left\{|{\varphi }_i\rangle \right\}}_{i=1}^N$ are the eigenstates of the N-level quantum system [23]. Usually, the states of two-level quantum systems are considered as arrows from the origin to points on the Bloch sphere [24].

The dynamical equation can be described as the following Schrödinger equation:

$$\begin{gathered} i\hslash \frac{d}{dt}|\psi \left(t\right)\rangle =H\left(t\right)|\psi \left(t\right)\rangle \\ \left|\psi \left(t=0\right)\rangle =\right|{\psi }_0\rangle \end{gathered}$$

(2)

where $\hslash$ is Plank constant (assume $\hslash =1$ in this paper), $H\left(t\right)$ is the system Hamiltonian and $i=\sqrt{-1}.$ The dynamics of the system are governed under the following Hamiltonian:

$$H\left(t\right)= H_0+H_c\left(t\right)=H_0+\sum _{m=1}^M{u}_m\left(t\right)H_m$$

(3)

where $H_0$ is the free Hamiltonian of the system and $H_c\left(t\right)$ is the time-dependent control Hamiltonian that represents the interaction of the system with the external control fields $u_m\left(t\right),$ $m=1,2,\dots ,M$ (scalar functions). Additionally, $H_m$ for $m=1,2,\dots ,M$ are Hermitian operators.

In practical applications, there exist external disturbances affecting the control fields. Assume that the system Hamiltonian is disturbed as follows:

$$H_{\Theta }\left(t\right)= f_0\left({\theta }_0\right)H_0+\sum _{m=1}^M{f}_m\left({\theta }_m\right)u_m\left(t\right)H_m$$

(4)

where functions $f_m\left({\theta }_m\right)$, $\left(m=0,1,\dots ,M\right)$ characterize uncertainty functions and $\Theta =\left({\theta }_0,{\theta }_1,\dots ,{\theta }_M\right).$ To compare and indicate the advantages of the proposed method, it is assumed that the situations and assumptions are similar to the system described in [19]. Therefore, let $f_m\left({\theta }_m\right),$ for $m=1,2,\dots ,M,$ be continuous functions and the parameters ${\theta }_m\in \left[1-E_m,1+E_m\right]$ could be time-dependent. For simplicity, one can assume that the uncertainty bounds $E_0=,\dots ,=E_m=,\dots ,=E_M=E$ are all equal in this paper. Additionally, let the nominal values of ${\theta }_m$ are 1 and the fluctuations of the uncertainty parameters ${\theta }_m$ be $2E$ (where $E\in \left[0,1\right]$).

The objective is to design the controls $\left\{u_m\left(t\right),m=1,2,\dots ,M\right\}$ to steer the quantum system with uncertainties from an initial state $|{\psi }_0\rangle$ to a target state $|{\psi }_{target}\rangle$ with high fidelity. The fidelity between two pure quantum states $|{\psi }_1\rangle$ and $|{\psi }_2\rangle$ is defined as [25]:

$$F(\left|{\psi }_1\rangle ,\right|{\psi }_2\rangle )=|\langle {\psi }_1|{\psi }_2\rangle |.$$

(5)

Suppose that a similar ensemble’s members with different Hamiltonians are given. The main objective is to drive the members from an initial state to a desired state. To control the ensemble, one can select a set of samples instead of all ensemble members and create an augmented system to be controlled. Let $\left\{H_{{\Theta }_n},n=1,2,\dots ,N\right\}$ be the Hamiltonian of the selected samples, where $N$ is the number of the training samples. The augmented system is constructed as follows:

$$\frac{d}{dt}\left(\begin{array}{c}|{\psi }_1\left(t\right)\rangle \\ |{\psi }_2\left(t\right)\rangle \\ ⋮\\ |{\psi }_N\left(t\right)\rangle \end{array}\right)=-i\left(\begin{array}{c}{H}_{{\Theta }_1}\left(t\right)|{\psi }_1\left(t\right)\rangle \\ H_{{\Theta }_2}\left(t\right)|{\psi }_2\left(t\right)\rangle \\ ⋮\\ H_{{\Theta }_N}\left(t\right)|{\psi }_N\left(t\right)\rangle \end{array}\right),$$

(6)

where ${\Theta }_n\in \left\{\left({\theta }_{0n_0},{\theta }_{1n_1},\dots ,{\theta }_{M{n}_M}\right),n_0=1,2,\dots ,N_0,\dots ,n_M=1,2,\dots ,N_M\right\}$ and $N={\prod }_{j = 0}^M{N}_j$ is number of the training samples. The task is to find the best control $u^{*}$ such that the performance function

$$J\left(u\right)=\frac{1}{N}\sum _{n=1}^N{|\langle {\psi }_n\left(t\right)|{\psi }_{n_{target}}\rangle |}^2$$

(7)

for each control strategy in $u=\left\{u_m\left(t\right),m=1,2,\dots ,M\right\}$, is maximized. Thus, the control problem can be formulated as a maximization problem as follows:

$$\begin{gathered} \max J\left(u\right)=\frac{1}{N}\sum _{n=1}^N{|\langle {\psi }_n\left(T\right)|{{\psi }_n}_{target}\rangle |}^2 \\ s.t. \frac{d}{dt}\left(\begin{array}{c}|{\psi }_1\left(t\right)\rangle \\ |{\psi }_2\left(t\right)\rangle \\ ⋮\\ |{\psi }_N\left(t\right)\rangle \end{array}\right)=-i\left(\begin{array}{c}{H}_{{\Theta }_1}\left(t\right)|{\psi }_1\left(t\right)\rangle \\ H_{{\Theta }_2}\left(t\right)|{\psi }_2\left(t\right)\rangle \\ ⋮\\ H_{{\Theta }_N}\left(t\right)|{\psi }_N\left(t\right)\rangle \end{array}\right), \\ \psi \left(t=0\right)\rangle =|{\psi }_0\rangle ,H_{{\Theta }_n}\left(t\right)= f_{0,n}\left({\theta }_{0,n}\right)H_0+\sum _{m=1}^M{f}_{m,n}\left({\theta }_{m,n}\right)u_m\left(t\right)H_m , n=1,2,\dots ,N \end{gathered}$$

(8)

when ${\theta }_{m,n}\in \left[1-E,1+E\right]$, $t\in \left[0,T\right]$ and $n=1,2,\dots ,N$.

Note that $J \left(u\right)$ depends on the control signal $u$, implicitly, subject to Schrödinger equation, be satisfied.

3. Quantum Genetic Learning Ensemble Control Algorithm

In this section a systematic methodology for control design of a quantum ensemble is presented during two training and testing steps. Solving Equation (8) by using QGA a quantum learning controller is designed.

3.1. Solving Process

If $u_m\left(t\right)=u_m$, $m=1,2,\dots ,M$ for $t\in \left[0,\Delta t\right]$ where $u_m$ is a constant, then according to the Schrodinger equation and time-evolution equation for each sample, from Equation (6) we have:

$$|{\psi }_n\left(\Delta t\right)\rangle =e^{-i\left(H_0{f}_0\left({\theta }_{0n_0}\right)+{\sum }_{m=1}^M{u}_m{f}_m\left({\theta }_{{mn}_m}\right)H_m\right)\mathsf{\Delta }t}|{\psi }_n\left(0\right)\rangle ,n=1,2,\dots ,N.$$

(9)

So, for $t\in \left[0,\Delta t\right]$ considering Equation (9), the objective function of Equation (8), changes to:

$$Max J\left(u\right)=\frac{1}{N}{\displaystyle \sum }_{n=1}^N{|\langle {\psi }_n\left(0\right)e^{-i\left(H_0{f}_0\left({\theta }_{0n_0}\right)+{\sum }_{m=1}^M{u}_m{f}_m\left({\theta }_{{mn}_m}\right)H_m\right)\mathsf{\Delta }t}|{\psi }_{n_{target}}\rangle |}^2.$$

(10)

Hence, $\left[0,T\right]$ is divided into Q subintervals and suppose that $u_m\left(t\right),$ $m=1,2,\dots ,M$ are constants in any subinterval with the same length $\Delta t=T/Q$. Let $|{\psi }_n{}^{j-1}\left(0\right)\rangle$ be the initial state of the control system in the $j$-th subinterval, then for $j$-th subinterval the following problem must be solved:

$$\mathrm{Max}\begin{array}{c}{J}^j\left(u\right)=\Vert \langle |e^{-i\left(H_0{f}_0\left({\theta }_{0n_0}\right)+{\sum }_{m = 1}^M{u}_m{f}_m\left({\theta }_{m{n}_m}\right)H_m\right)\mathsf{\Delta }t}{\psi }_n{}^{j - 1}\left(0\right){|{\psi }_n{}_{target}^j\rangle \Vert }^2\end{array},$$

(11)

where

$$|{\psi }_n{}_{target}^j\rangle =\frac{|{\psi }_n\left(0\right)\rangle +j\frac{|{\psi }_{n_{target}}\rangle -|{\psi }_n\left(0\right)\rangle }{Q}}{\Vert |{\psi }_n\left(0\right)\rangle +j\frac{|{\psi }_{n_{target}}\rangle -|{\psi }_n\left(0\right)\rangle }{Q}\Vert }$$

(12)

is the target state of $j$-th subinterval for $n$-th sample. In each subinterval, Equation (11), by QGA is solved and the best control $u_m^{*j}$, $m=1,\dots ,M$ is obtained. Then, for $j=1,\dots ,Q,$

$$|{\psi }_n{}^j\rangle =e^{-i\left(H_0{f}_0\left({\theta }_{0n_0}\right)+{\sum }_{m=1}^M{u}_m^{*j}{f}_m\left({\theta }_{{mn}_m}\right)H_m\right)\mathsf{\Delta }t}|{\psi }_n{}^{j-1}\left(0\right)\rangle$$

(13)

is the state transferred by optimal control $u_m^{*j}$, $m=1,2,\dots ,M$ in the $j$-th subinterval, which is considered as the initial state of the next subinterval, that is, $|{\psi }_n{}^j\left(0\right)\rangle =|{\psi }_n{}^j\rangle$ is the initial state of the(j + 1)-th subinterval, and the process continues.

3.2. Structure of Quantum Chromosomes

The smallest unit of information stored in a two-state quantum unit is called a quantum bit or qubit, which can be in a superposition of states. QGA is an algorithm based on the concepts of qubit and superposition of the states in quantum mechanics theory [22]. A chromosome is made as a string of $m$ qubits that forms a quantum register. Additionally, the $j$-th individual chromosome of the $t$-th generation can be indicated as

$$u_j^t=\left[\begin{array}{cccc}{\alpha }_{11}^{jt}& {\alpha }_{12}^{jt}& \dots & {\alpha }_{1k}^{jt}\\ {\beta }_{11}^{jt}& {\beta }_{12}^{jt}& \dots & {\beta }_{1k}^{jt}\end{array}\right|\begin{array}{c}{\alpha }_{21}^{jt}\\ {\beta }_{21}^{jt}\end{array}\begin{array}{c}{\alpha }_{22}^{jt}\dots \\ {\beta }_{22}^{jt}\dots \end{array}\begin{array}{c}{\alpha }_{2k}^{jt}\\ {\beta }_{2k}^{jt}\end{array}|\begin{array}{c}\dots \\ \dots \end{array}|\dots \dots \begin{array}{c}{\alpha }_{m1}^{jt}\\ {\beta }_{m1}^{jt}\end{array}\begin{array}{c}{\alpha }_{m2}^{jt}\\ {\beta }_{m2}^{jt}\end{array}\begin{array}{c}\dots {\alpha }_{mk}^{jt}\\ \dots {\beta }_{mk}^{jt}\end{array}]$$

(14)

where $m$ indicates the number of genes in any chromosomes and $k$ represents the number of qubits encoding each gene. In the initial generation (when $t=0$), quantum encoding ($\alpha$,$\beta$) of each individual in the population is initialized with $(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$, which denotes that the probability of collapsing the superposed state into each basic states is equal.

3.3. Quantum Rotating Gates

Unlike the conventional genetic algorithm that uses a crossover operation, the quantum genetic algorithm applies the probability amplitude of qubits to encode chromosomes and uses quantum rotating gates to update generations. The genetic utilization of the quantum genetic algorithm is mainly through acting on the superposition state or entanglement state by the quantum rotating gates to change the probability amplitude. Accordingly, the construction of quantum rotating gates is the key issue of the quantum genetic algorithm, and it directly affects the performance of the algorithm. Quantum rotating gates can be organized according to the practical problems and usually can be defined as [26]

$$R\left({\xi }_i\right)=\left[\begin{array}{c}\cos ({\xi }_i)-\sin \left({\xi }_i\right)\\ \sin \left({\xi }_i\right) \cos ({\xi }_i)\end{array}\right].$$

(15)

Therefore, the updating process is defined as follows:

$$\left[\begin{array}{c}{\alpha }_i^{\prime }\\ {\beta }_i^{\prime }\end{array}\right]=R\left({\xi }_i\right)\left[\begin{array}{c}{\alpha }_i\\ {\beta }_i\end{array}\right]=\left[\begin{array}{c}\cos ({\xi }_i)-\sin \left({\xi }_i\right)\\ \sin \left({\xi }_i\right)\hspace{1em}\cos ({\xi }_i)\end{array}\right]\left[\begin{array}{c}{\alpha }_i\\ {\beta }_i\end{array}\right]$$

(16)

where ${\left({\alpha }_i,{\beta }_i\right)}^T$ and ${\left({\alpha }_i^{\prime },{\beta }_i^{\prime }\right)}^T$ are the probability amplitudes of the 𝑖-th qubit in a chromosome before and after the quantum rotating gates update, respectively. Additionally, ${\theta }_i$ is the rotating angle. In

Table 1. Adjustment strategy of rotating angle.

${\mathit{x}}_{\mathit{i}}$	$\mathbf{R}\mathbf{e}{\mathbf{f}}_{\mathit{i}}$	$\mathit{f}\left(\mathit{x}\right)>\mathit{f}\left(\mathbf{R}\mathbf{e}\mathbf{f}\right)$	$\mathbf{\Delta }{\mathit{\theta }}_{\mathit{i}}$	$\mathit{s}\left({\mathit{\alpha }}_{\mathit{i}},{\mathit{\beta }}_{\mathit{i}}\right)$
				${\mathit{\alpha }}_{\mathit{i}}{\mathit{\beta }}_{\mathit{i}}>0$	${\mathit{\alpha }}_{\mathit{i}}{\mathit{\beta }}_{\mathit{i}}<0$	${\mathit{\alpha }}_{\mathit{i}}$ = 0	${\mathit{\beta }}_{\mathit{i}}$ = 0
0	0	FALSE	0	0	0	0	0
0	0	TRUE	0	0	0	0	0
0	1	FALSE	$\Delta {\theta }_i$	+1	−1	0	±1
0	1	TRUE	$\Delta {\theta }_i$	−1	+1	±1	0
1	0	FALSE	$\Delta {\theta }_i$	−1	+1	±1	0
1	0	TRUE	$\Delta {\theta }_i$	+1	−1	0	±1
1	1	FALSE	0	0	0	0	0
1	1	TRUE	0	0	0	0	0

, the updating strategies, for the chromosomes, are presented. The value and the sign of ${\theta }_i$ are determined by the adjustment strategy. Here, $x_i$ is the $i$-th bit of the current chromosome; ${\mathrm{Ref}}_i$ is the $i$-th bit of the current optimal binary solution, named the reference binary solution, that all quantum chromosomes should be steered toward its corresponding chromosome; $f\left(x\right)$ is the fitness function; $s\left({\alpha }_i,{\beta }_i\right)$ is the rotate direction of the rotating angle and $\Delta {\theta }_i$ is the increment value of the $i$-th rotating angle. The value of $\Delta {\theta }_i$ is a constant and is usually around $0.01\pi$. The overall process in QGA is similar to the GAs but with some differences in changing from one generation to the next one. In fact, a new generation $P\left(t\right)$ is achieved by operating quantum rotating gates on any individuals.

A genetic type-based iterative learning algorithm is shown in Algorithm 1. The algorithm is written according to Section 3.1.

Algorithm 1. Genetic Type Based Iterative Learning Algorithm

set $j=1$ (counter of subintervals)

set $|{\psi }^{j - 1}\left(0\right)\rangle =|\psi \left(0\right)\rangle$

$|{\psi }_n{}_{target}^j\rangle =\frac{|{\psi }_n\left(0\right)\rangle +j\frac{|{\psi }_{n_{target}}\rangle -|{\psi }_n\left(0\right)\rangle }{Q}}{\Vert |{\psi }_n\left(0\right)\rangle +j\frac{|{\psi }_{n_{target}}\rangle -|{\psi }_n\left(0\right)\rangle }{Q}\Vert }$ (target state)

Repeat (for each subinterval)

Choose a set of arbitrary controls $u_m^{j0}$, $m=1,2,\dots ,m$

Solve problem (11) by using QGA and find $u_m^{j*}$ , $m=1,2,\dots ,m$

$|{\psi }_n{}^j\rangle =e^{-i\left(H_0{f}_0\left({\theta }_{0n_0}\right)+{\sum }_{k=1}^M{u}_k^{*j}{f}_k\left({\theta }_{k{n}_k}\right)H_k\right)\mathsf{\Delta }t}|{\psi }_n{}^{j - 1}\left(0\right)\rangle$

$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}|{\psi }_n{}^j\left(0\right)\rangle :=|{\psi }_n{}^j\rangle$

$j=j+1$

Until $j=Q$

The optimal control $u_m^{*}=\{u_m^{j*}, j=1,2,\dots ,Q\}$ , $m=1,2,\dots ,M$

Additionally, in Figure 1, a schematic diagram of the proposed method is given. In this diagram, first, a random population of quantum chromosomes $P\left(t\right)$ is generated. A binary population $P_b\left(t\right)$ by measuring the present population is obtained. After evaluating $P_b\left(t\right)$ and specifying the best solution $\mathrm{Ref}$, the whole of the quantum chromosomes are rotated toward the corresponding chromosome of $\mathrm{Ref}$, according to Table 1. This process generates a new population with better fitness. As indicated in Figure 1, the above processes are repeated until the stop criterion is satisfied for all $j=1,2,\dots ,Q$.

4. Simulation Results

In this section two examples are simulated. Assume that all of the control signals are bounded in a known interval $\left[u_{min},u_{max}\right]$.

Objective and protocols of simulation are explained as follows:

Let $\left[u_{min},u_{max}\right]=\left[-4, 6\right],$ the initial state $|\psi \left(0\right)\rangle =\left(0,0,1\right)$ in real coordinates $(i.e.,|{\psi }_0\rangle ={\left[10\right]}^t),$ the time interval $\left[0, 5\right]$ ($T=5$) is divided by $Q=20$ and time slices $\Delta t=0.25$. Additionally, the quantum genetic populations are the input control signals. The evolution generation number, the size of the population and the length of the each quantum chromosome are 200, 100, and 24, respectively. The mutation rate is 0.05 and the selection percentage of individuals is $50\%.$ The stop condition for the iterative algorithm is considered as $\left|1-J\left(u\right)\right|<\epsilon$ ($\epsilon$ = 0.001). The objective of the problem-solving is transferring all of the initial states to the target state $|\psi \left(T\right)\rangle =\left(0,0,-1\right)(i.e.,|{\psi }_T\rangle ={\left[01\right]}^t)$, with maximum fidelity. The value of $\Delta {\theta }_i$ is set $0.01\pi$.

Example 1:

Consider the following two level quantum systems:

$$\begin{gathered} i\frac{d}{dt}|\psi \left(t\right)\rangle =\left(f_0\left({\theta }_0\right)H_0+\sum _{m =1}^2{f}_m\left({\theta }_m\right)u_m\left(t\right)H_m\right)|\psi \left(t\right)\rangle \\ \left|\psi \left(t=0\right)\rangle =\right|{\psi }_0\rangle \end{gathered}$$

(17)

where $H_0=\frac{1}{2}{\sigma }_z=\frac{1}{2}\left(\begin{array}{c}1\hspace{1em}0\\ 0\hspace{0.5em}-1\end{array}\right)$ is the free Hamiltonian and $H_1=\frac{1}{2}{\sigma }_x=\frac{1}{2}\left(\begin{array}{c}0 1\\ 1 0\end{array}\right)$, $H_2=\frac{1}{2}{\sigma }_y=\frac{1}{2}\left(\begin{array}{c}0\hspace{0.5em}-i\\ i\hspace{1em}0\end{array}\right).$ Additionally, ${\sigma }_x=\left(\begin{array}{c}0 1\\ 1 0\end{array}\right)$, ${\sigma }_y=\left(\begin{array}{c}0\hspace{0.5em}-i\\ i\hspace{1em}0\end{array}\right)$, and ${\sigma }_z=\left(\begin{array}{c}1\hspace{1em}0\\ 0\hspace{0.5em}-1\end{array}\right)$ are Pauli matrices. Assume that the system’s state is written as

$$|\psi \left(t\right)\rangle =c_1\left(t\right)|1\rangle +c_2\left(t\right)|2\rangle$$

(18)

where $B=\left\{|1\rangle ,|2\rangle \right\}$ is the orthonormal basis of the corresponding Hilbert space. Let $C\left(t\right)=\left(c_1\left(t\right),c_2\left(t\right)\right)$, where $c_i\left(t\right)$ are complex time depended coefficients. Therefore, Equation (17) is equivalent to

$$i\dot{C}\left(t\right)=(f_0\left({\theta }_0\right)H_0+{\sum }_{m=1}^2{f}_m\left({\theta }_m\right)u_m\left(t\right)H_m)C\left(t\right).$$

(19)

In this example, let $f_m\left({\theta }_m\right)=\left(1-2{\theta }_m{}^2\right)\exp (-{\theta }_m{}^2/2$) be the Mexican hat wavelet functions for $m=1,2$ and $f_0\left({\theta }_0\right)=1$ on $\left[1-E,1+E\right]$ for E = 0.21. After sampling the uncertainty parameters, every sample can be described as follows:

$$\left(\begin{array}{c}{\dot{c}}_1\left(t\right)\\ {\dot{c}}_2\left(t\right)\end{array}\right)=-i\left(\begin{array}{c}0.5f_0\left({\theta }_0\right) G\left({\theta }_1,{\theta }_2\right)\\ G^{*}\left({\theta }_1,{\theta }_2\right) -f_0\left({\theta }_0\right)\end{array}\right)\left(\begin{array}{c}{c}_1\left(t\right)\\ c_2\left(t\right)\end{array}\right)$$

(20)

where $G\left({\theta }_1,{\theta }_2\right)=0.5(f_1\left({\theta }_1\right)u_1\left(t\right)-f_2\left({\theta }_2\right)u_2\left(t\right)i)$ and ${\theta }_i$ ∈ $\left[1-E,1+E\right]$. Additionally, $G^{*}$ is the complex conjugate of $G$. To construct an augmented system for the training step of the SLC method, consider N training samples that are selected through sampling the uncertainties, as follows:

$$\left(\begin{array}{c}{\dot{c}}_{1,n}\left(t\right)\\ {\dot{c}}_{2,n}\left(t\right)\end{array}\right)=-i\left(\begin{array}{c} 0.5f_0\left({\theta }_{0,n}\right) G\left({\theta }_{1,n},{\theta }_{2,n}\right)\\ G^{*}\left({\theta }_{1,n},{\theta }_{2,n}\right) -f_0\left({\theta }_{0,n}\right)\end{array}\right)\left(\begin{array}{c}{c}_{1,n}\left(t\right)\\ c_{2,n}\left(t\right)\end{array}\right), n=1,2,\dots ,N.$$

(21)

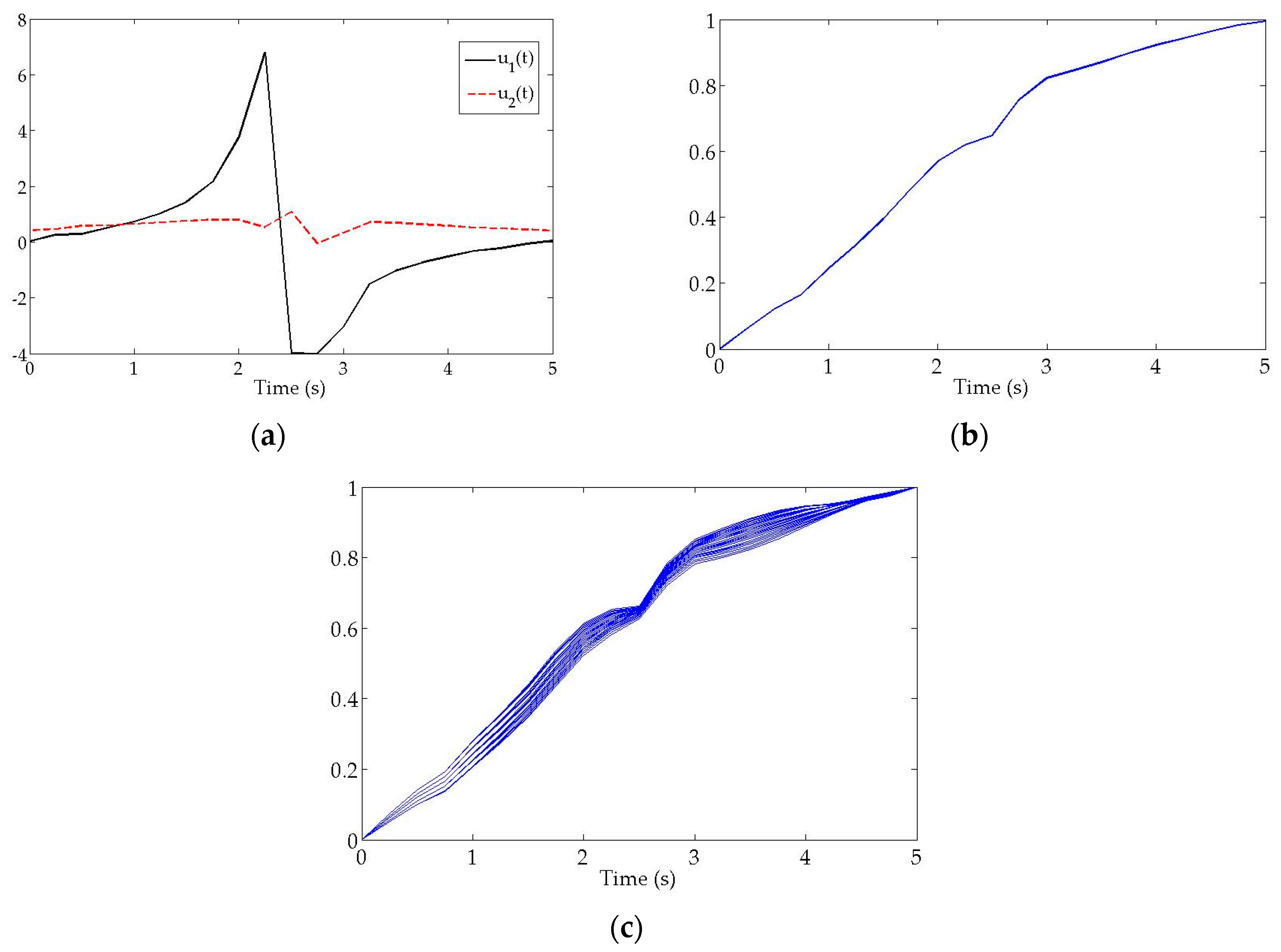
The results of simulation are illustrated in Figure 2. Figure 2a illustrates the control signals $u_m\left(t\right)$, $m=1,2$ obtained in the training step.

Figure 2b illustrates the mean of fidelity function of any states as a fitness function of the QGA. Finally, Figure 2c illustrates simultaneously steering ensemble members to the desired state. As simulation results indicate, 25 training samples are steered to the target state with a fidelity amplitude 0.9986 and error = 0.001. After running the control system, with founded control signals of the training step, for 200 test samples the fidelity amount is 0.9968 and the corresponding error is 0.003.

Example 2:

The second example is a three-level quantum system with uncertainties in Hamiltonian parameters that are found widely in natural and artificial atoms. Some atoms can be explained by a V-type three-level quantum system model. It is important to reach a robust preparation of this class of states for practical applications of quantum technology. The SLC, contributed with QGA, is used for a V-type quantum control system. Assume the initial state is:

$$|\psi \left(t\right)\rangle =c_1\left(t\right)|1\rangle +c_2\left(t\right)|2\rangle +c_3\left(t\right)|3\rangle$$

(22)

with $B=\left\{|1\rangle ,|2\rangle ,|3\rangle \right\}$, the orthonormal basis of the corresponding Hilbert space. Let $C\left(t\right)=\left(c_1\left(t\right),c_2\left(t\right),c_3\left(t\right)\right)$, where $c_i\left(t\right)$ are complex numbers. Then we have

$$i\dot{C}\left(t\right)=(f_0({\theta }_0)H_0+{\sum }_{m=1}^4{f}_m({\theta }_m)u_m\left(t\right)H_m)C\left(t\right).$$

(23)

We take $H_0$ = diag(1.5, 1, 0) as the free Hamiltonian and choose $H_1$, $H_2$, $H_3$, and $H_4$ as follows:

$$H_1=\left(\begin{array}{c}0 1 0\\ 1 0 0 \\ 0 0 0\end{array}\right), H_2=\left(\begin{array}{c}0-i 0\\ i 0 0 \\ 0 0 0\end{array}\right), H_3=\left(\begin{array}{c}0 0 1\\ 0 0 0 \\ 1 0 0\end{array}\right), H_4=\left(\begin{array}{c}0 0-i\\ 0 0 0 \\ i 0 0\end{array}\right).$$

(24)

After sampling the uncertainty parameters, every sample can be described as follows:

$$\left(\begin{array}{c}{\dot{c}}_1\left(t\right)\\ {\dot{c}}_2\left(t\right)\\ {\dot{c}}_3\left(t\right)\end{array}\right)=-i\left(\begin{array}{c}1.5f_0\left({\theta }_0\right)\hspace{1em}G\left({\theta }_1,{\theta }_2\right)\hspace{1em}G\left({\theta }_3,{\theta }_4\right)\\ G^{*}\left({\theta }_1,{\theta }_2\right)\hspace{1em}{f}_0\left({\theta }_0\right) \hspace{1em}0\hspace{0.5em}\\ G^{*}\left({\theta }_3,{\theta }_4\right)\hspace{1em}0\hspace{1em} 0\hspace{1em}\end{array}\right)\left(\begin{array}{c}{c}_1\left(t\right)\\ c_2\left(t\right)\\ c_3\left(t\right)\end{array}\right),$$

(25)

where $G\left({\theta }_1,{\theta }_2\right)=f_1\left({\theta }_1\right)u_1\left(t\right)-f_2\left({\theta }_2\right)u_2\left(t\right)i$, $G\left({\theta }_3,{\theta }_4\right)=f_3\left({\theta }_3\right)u_3\left(t\right)-f_4\left({\theta }_4\right)u_4\left(t\right)i$, and ${\theta }_i$ ∈ [1 − E, 1 + E]. E ∈ [0,1] is a given constant and $G^{*}$ is the complex conjugate of $G$. Comparing the results with previous works, uncertainty coefficients are chosen the same as what is given in [19], that is, $f_m\left({\theta }_m\right)={\theta }_m$ and $f_0\left({\theta }_0\right)={\theta }_0$ have uniform distributions over $\left[0.79,1.21\right].$ To construct an augmented system for the training step of the SLC design, we choose $N$ training samples (denoted as $n=1,2,\dots ,N$) through sampling the uncertainties as follows:

$$\left(\begin{array}{c}{\dot{c}}_{1,n}\left(t\right)\\ {\dot{c}}_{2,n}\left(t\right)\\ {\dot{c}}_{3,n}\left(t\right)\end{array}\right)=-i\left(\begin{array}{c} 1.5f_0\left({\theta }_{0,n}\right) G\left({\theta }_{1,n},{\theta }_{2,n}\right) G\left({\theta }_{3,n},{\theta }_{4,n}\right) \\ G^{*}\left({\theta }_{1,n},{\theta }_{2,n}\right) f_0\left({\theta }_{0,n}\right) 0 \\ G^{*}\left({\theta }_{3,n},{\theta }_{4,n}\right) 0 0 \end{array}\right)\left(\begin{array}{c}{c}_{1,n}\left(t\right)\\ c_{2,n}\left(t\right)\\ c_{3,n}\left(t\right)\end{array}\right)$$

(26)

where $G\left({\theta }_{1,n},{\theta }_{2,n}\right)=f_1\left({\theta }_{1,n}\right)u_1\left(t\right)-f_2\left({\theta }_{2,n}\right)u_2\left(t\right)i$ and $G\left({\theta }_3,{\theta }_4\right)=f_3\left({\theta }_{3,n}\right)u_3\left(t\right)-f_4\left({\theta }_{4,n}\right)u_4\left(t\right)i$. Now, the objective is to find a robust control strategy $u\left(t\right)=\left\{u_m\left(t\right),m=1,2,3,4\right\}$ to drive the quantum system from $|{\psi }_0\rangle =|1\rangle$ (i.e., $C_0=\left(1,0,0\right))$ to $|{\psi }_{target}\rangle =\left(1/\sqrt{2}\right)\left(|2\rangle +|3\rangle \right)$ (i.e., $C_{target}=\left(0,1/\sqrt{2},1/\sqrt{2}\right)$). The general conditions here are similar to ones mentioned in previous example but $Q=10$. Apart from the initial values, the results are always converged and it is more precise than the gradient method as shown in

Table 2. Comparison between the results of QGA and gradient algorithm.

Method	Training Error	Test Error
Gradient based learning control	0.004	0.08
Quantum Genetic algorithm	0.002	0.005

.

The training error is computed as $\left|1-J\left(u^{*}\left(T\right)\right)\right|$ in which $J\left(u^{*}\left(T\right)\right)$ is the fidelity function for training samples. For calculating the test error, optimal control $u^{*}$ is implemented to the test samples, which are selected randomly. Additionally, the amount of $\left|1-J\left(u^{*}\left(T\right)\right)\right|$ is computed for test samples, as a test error index. The method presented in this paper always converges and does not depend on initial choices of $u=\left\{u_m\left(t\right),m=1,2,\dots ,M\right\}.$ Figure 3a–c demonstrate the control signals $u_m\left(t\right)$, $m=1,2,3,4$ and fidelity function for steering training samples simultaneously to the target state.

The training samples are steered to the target state with a fidelity of 0.9982. The control values found in training step are applied on 200 testing samples. The fidelity amount of 0.9954 is achieved with a test error equal to 0.005. Figure 3a,b show the control signals $u_1\left(t\right)$, $u_2\left(t\right)$, $u_3\left(t\right)$, and $u_4\left(t\right)$ through the time interval $\left[0,5\right]$ and Figure 3c illustrates the mean of the fidelity function of all of the states as a fitness function of QGA.

5. Conclusions

In this paper a new quantum genetic sampling-based learning controller is designed. For this purpose an unconstrained nonlinear optimization problem is designed and is solved by a new quantum genetic algorithm. All of the members of an inhomogeneous quantum ensemble transfers to a known target state, simultaneously. In this method controller performance is independent of the initial input values and this is an important advantage of the proposed method as compared with gradient-based learning methods. Additionally, transfer process errors and learning iteration numbers are reduced, significantly. A couple of examples for two- and three-level quantum systems are simulated by using the proposed method. The simulation results indicate the advantages and efficiency of the presented method.