1. Introduction
Generally, amplitude-modulated and/or frequency-modulated (AM-FM) multi-component signals collected by sensors are interfered with by background noise, resulting lower signal-to-noise ratio (SNR) [
1]. The reason for the low SNR signals obtained by a determinate acquisition system are usually as follows: firstly, when a rolling bearing is in the infantile fault period, the fault feature is inconspicuous and buried in the background noise. Secondly, signal energy as well as incipient failure features will attenuate because of the long distance between the fault source and the sensor, which usually is located on the bearing pedestal. Moreover, the characteristic signal will also be attenuated when there is a long transmission path from the sensor to the acquisition device [
2]. Thirdly, the signals collected by sensors contain strong background noise. The main transmission system of a machine is a complex system composed of multiple components such as motors, couplings, multiple reduction gearbox. The vibration of all components will be collected by the sensor. Noisy signals make it difficult to identify the fault features in signal processing, therefore, it is necessary to perform denoising and characterize fault feature accurately on the low SNR vibration signal.
In the last few decades, many theoretical denoising methods have been proposed and are widely used in medical signaling, image processing and mechanical engineering signal processing [
3,
4,
5]. Donolo and John-stone [
6], taking the advantage of the spatial diversity of wavelet basis functions, proposed a denoising method with a threshold based on wavelet transform. Their methods concentrate the energy of the ideal signal, benefiting from the effective wavelet, guaranteeing a certain de-noising effect. However, the selection of threshold functions is the main problem with wavelet de-noising algorithms, which usually generate a deviation between the calculated result and the real one. Empirical mode decomposition (EMD) [
7] can be treated as a typical adaptive signal decomposition method of frequency-selection and filtering. The signal is decomposed into a series of intrinsic mode functions (IMFs) arranged from high frequency to low frequency. The source signal can be processed by abandoning high-frequency components for the consideration that noise components are generally distributed in the high-frequency domain. However, as EMD has the defects of modal aliasing, the ideal signal and noise coexist in the selected IMFs. This would result in the loss of useful information. Ensemble empirical mode decomposition (EEMD) [
8] was developed to solve the mode-mixing problem of EMD by adding noise to the source signal. It is more accurate and effective for data decomposition than EMD, but it prompts new trouble by being time consuming. Variable mode decomposition (VMD) [
9,
10] is a signal decomposition method based on wiener filtering, one dimensional Hilbert transform and heterodyne demodulation analysis, but the decomposition results are restricted by the selection of penalty parameters and the number of components. Singular value decomposition (SVD) [
11], as a data-processing method without prior knowledge, has been successfully applied to signal denoising and proved to be effective. However, there exist two pivotal problems: one is that how to determine the effective rank order after decomposition, and the other one is that how to achieve the reconstruction matrix. Meanwhile, the noise reduction effect of SVD is not prominent when analyzing the low SNR signal.
Dynamic mode decomposition (DMD) [
12] is an equation-free Koopman frequency analysis technique based on the theory of SVD and mode decomposition. It can extract the spatiotemporal coherent characteristics by decomposing a dynamic model into a series of single-frequency non-orthogonal modes based on its inherent space-time. The reconstructed signal can characterize the useful information of the original signal perfectly by superposing the filtered modes according to time coefficients. The algorithm is suitable for extracting dynamic information of nonlinear systems [
13]. The instantaneous components and high-frequency noise components can be effectively removed, due to the dynamic delay processing in the algorithm [
12]. The DMD algorithm has been well applied in the fluid mechanics community. Rowley [
12] applied DMD in the jet cross flow field. The results show that DMD theory can extract the shedding frequency while the linear stability analysis method cannot. In addition, DMD can separate the shear layer and wall vortices, whereas the proper orthogonal decomposition (POD) algorithm is ineffective. Schmidt [
13] applied DMD to the flow field in a variety of environmental conditions, indicating that the DMD theory is effective for feature extraction with numerical simulation and measured velocity field data. Moreover, DMD can separate video frames into a background and multiple foregrounds successfully when applied to video processing [
14]. DMD can also be used for biometrics to detect fraudulent samples [
15]. In the field of robotics and neuroscience, DMD has been used to estimate the perturbation of human-robot interactions [
16], and the coherent modes in large-scale neural recording have been extracted [
17]. Nowadays, theoretical research with DMD mainly focuses on two aspects. In the first aspect, a variety of improved methods are proposed based on the standard DMD to solve the problem that DMD cannot accurately extract the dynamic information due to the influence of signal noise. These strategies range from noise-corrected dynamic mode decomposition with control [
18], total least-squares DMD [
19], compressed sensing DMD [
20] to sparsity-promoting DMD [
21]. The improved DMD algorithm can extract fluid dynamic information more accurately in varying degrees. In the second aspect, in view of the large data processing problems, researchers aim at reducing the computational complexity and the program storage space in either pre-processing or post-processing, using strategies including random DMD [
22], random low-rank DMD [
23], and tensor-based DMD [
24]. The standard DMD and its improved algorithm are more suitable in analyzing periodic or quasi-periodic signals, but it is prone to generate some false mode components. Therefore, the theory of fault vibration signal processing and fault mode recognition with DMD needs further study.
Essentially, DMD is a hybrid algorithm based on mode decomposition and SVD, and it inevitably inherits the drawbacks of these two algorithms, including the selection strategy of truncated rank order and DMD modes. The number of truncation rank for the similar matrix needs to be artificially and blindly selected in advance; whether the number value is appropriate or not is of crucial importance for accurately representing the dynamic information of reconstructed signal. The measured vibration signal with the characteristic of non-linear and non-stationary is coupled with multi-components and contain strong environmental noise. To achieve the purpose of fault feature extraction with DMD, it requires separation of the fault feature components effectively from the DMD modes. It is necessary to establish an adaptive optimization algorithm based on DMD to achieve an accurate truncation of rank and screen the single-frequency non-orthogonal modes effectively.
In this paper, an optimized DMD algorithm is proposed for extracting the fault features drowned in the multi-component coupled and noisy mechanical signal. The idea of sparse optimization is adopted to select the optimal rank for the solution of truncated rank order selection problem. By introducing the constraint of non-convex regulation to the rank function, the similar matrix has low rank attribute, making the ideal components (signals) more centralized. As for the fact that the noise’s multiscale permutation entropy (MPE) is larger than the ideal component’s, the low rank modes are selected corresponding to faults and inherent features by a threshold, solving the difficulty in selecting useful DMD modes. Then the signal is reconstructed by the low rank DMD modes, and Fourier transform (FT) is conducted to achieve the purpose of denoising and fault diagnosis of the noisy mechanical signal.
The structure of this paper is as follows.
Section 2 introduces the basic theory, including the standard algorithm of DMD, the sparse optimization algorithm with non-convex optimization regulation, and MPE. In
Section 3, the proposed algorithm is applied to the normal and faulty bearing noisy simulation signals to verify its effectiveness. Analysis results of two experimental bearing fault signals are described in
Section 4. Conclusions are summarized in
Section 5.
3. Algorithm Application in Fault Bearing Simulation Signal
Here we adopt the dynamic model of bearing fault signal established by Randall [
40]. The mathematical model of fault rolling bearing is described in Equation (19). According to the characteristics of bearing structure, instantaneous impact signal should be generated when bearing parts pass through the fault location. The impact motivates the bearing system oscillating by its natural frequency with high-frequency attenuation. Define
as a period of two intervals,
as the natural frequency oscillation function, and
as the
-th amplitude of shock response. The interference of additive noise
(zero mean additive background noise) should be taken into consideration in the simulation signal in view of poor working environment of rolling bearings. Therefore, the mathematical model of fault rolling bearing can be described as:
where
is the
k-th impact energy;
and
are the initial phases;
is the modulation frequency;
is the attenuation coefficient depended on the bearing system;
is the time lag from its mean period due to the presence of tiny fluctuation, and
is a random constant.
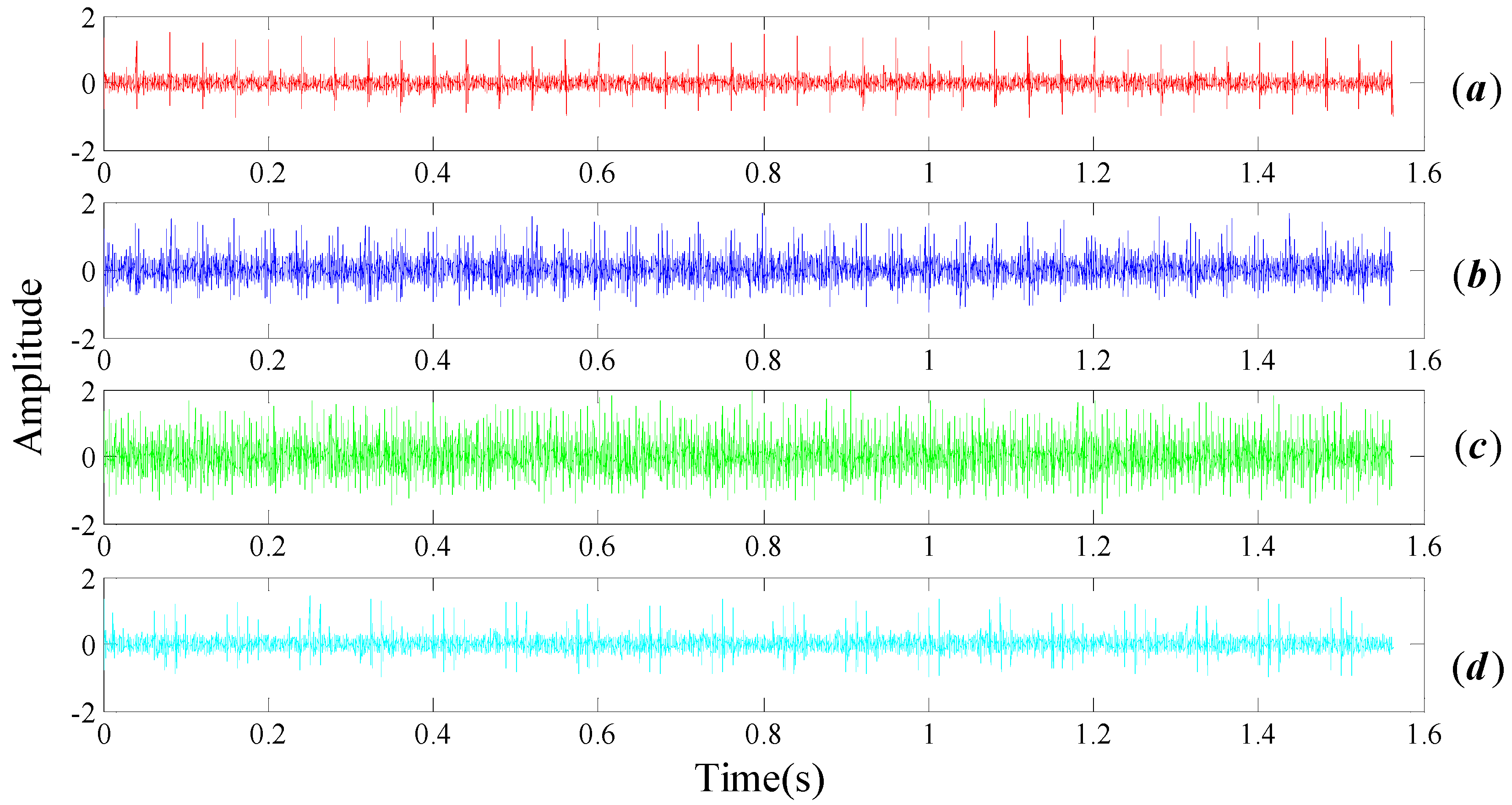
Time domain simulation signals of rolling bearing with normal bearing and inner race, outer race and roller faults are respectively plotted in
Figure 3. It should be pointed out that Gaussian white noise is added so as to SNR reach to 0.5 precisely. The parameters selection of Equation (19) is listed in
Table 1, where
and
are denoted as rotational frequency and cage frequency.
,
,
respectively represent the failure frequency of the inner circle, the outer ring, and the rolling element. The sampling frequency is selected as 5 KHz, and the number of total sampling points is 8000.
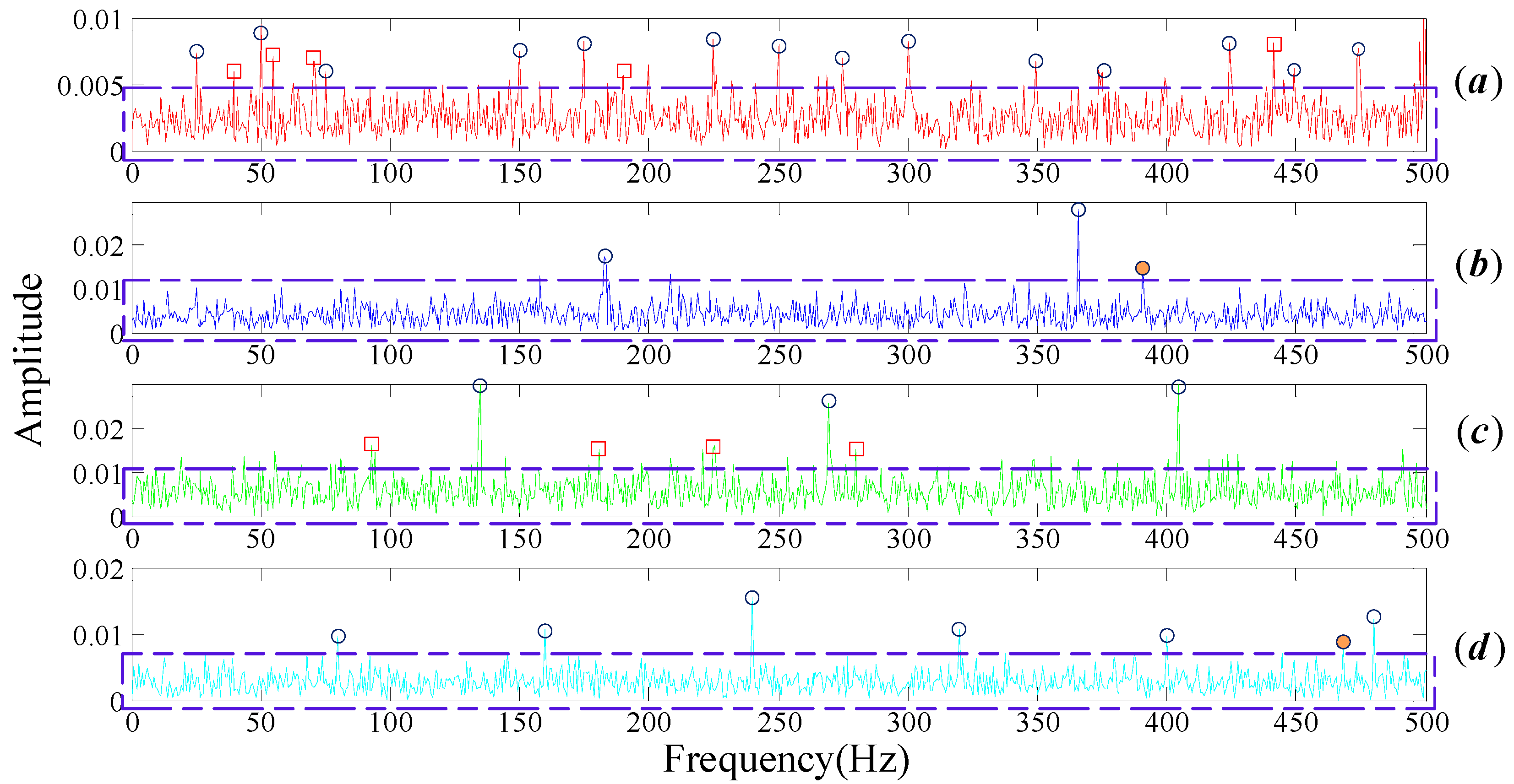
The FT spectrum analysis of the bearing noisy signal is shown in
Figure 4. There are a large number of noisy spectral components, as shown by the blue dotted boxes in
Figure 4a–d, which severely affect the feature identification of the fault. Rotational frequency and its resonance frequencies (as marked in blue circles in
Figure 3a) should be easy to recognize in the spectrum domain when the bearing is under healthy conditions. However, numbers of noise frequencies revolve around the center frequencies, as marked in the brown dotted box in
Figure 3a, resulting in the fact that we cannot interpret the signal properly. The same situation appears in the bearing inner race fault signal spectrum, as shown in
Figure 3c. In general, the three common types of faults on the inner race, the outer race and the rolling elements can be modeled as
,
,
, respectively. That is to say, rotational frequency, 0, cage frequency should modulate their center frequency, respectively. In
Figure 3b,d, the center frequency belongs to the inner race and balls can be identified, but it is difficult to identify their respective modulation frequency as they are submerged by the noise components.
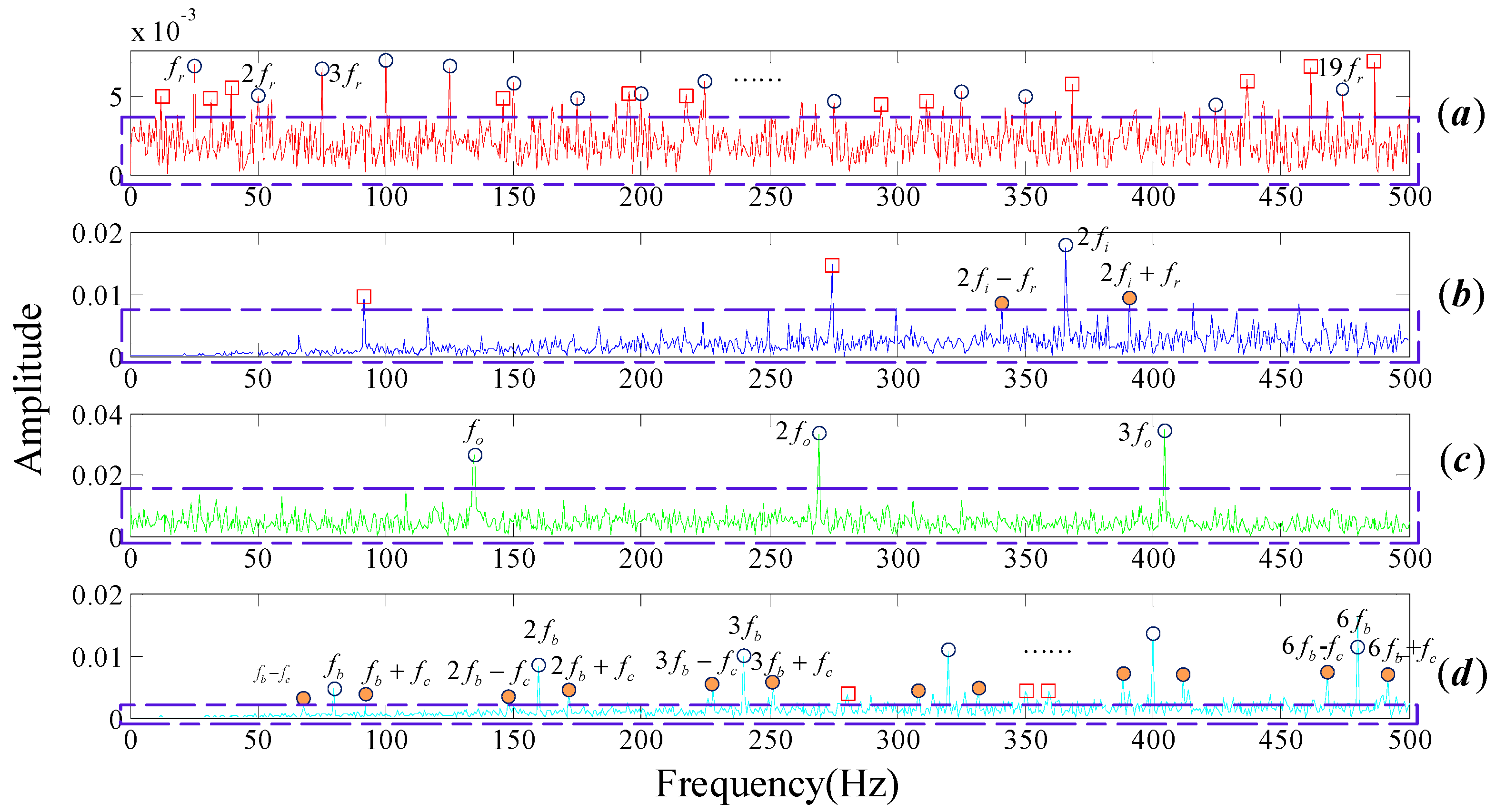
In this paper, the parameters
are selected as 1.2, 0.5 respectively in the process of sparse optimization using non-convex optimization regularization. The MPE threshold is selected as 0.7 (refer to the conclusion section). We recover the signals by DMD modes whose MPE values are less than the threshold. Spectrums were obtained by performing FT on the reconstruction signals, as shown in
Figure 5.
Meanwhile, in order to illustrate the effectiveness of our method, multi-scale wavelet transform is applied on the four noisy signals by taking the wavelet function db1, WT results are shown in
Figure 6. Though it is obvious that the harmonic frequencies of
and
can be identified in
Figure 6a,c, there are still some frequencies attributed by the noise involving around the mid-frequencies, as can we see in the brown dotted box. Meanwhile the spectra of the proposed algorithm are cleaner and more readable then the results of FT and WT. Not only can we pick out their center and modulation frequencies in
Figure 5, but also there is few noise frequencies surrounding them. Our method has tremendous advantages in both de-noising and fault feature extraction compared with FT and WT.
4. Algorithm Application in Experimental Signals of Rolling Bear
Signals of bearing systems collected by sensors from practice spots are much more complex than the simulation signals, which contain multi-component signals and background noises transmitted by other components. In order to verify the effectiveness of the proposed algorithm in signal de-noising and fault diagnosis, we apply the proposed algorithm to the actual bearing signals. We test the bearing signals from two experimental environments. First, the bearing signal is from the published bearing test data at the university of Cincinnati [
41]; the second comes from our rotating machinery vibration analysis test rig.
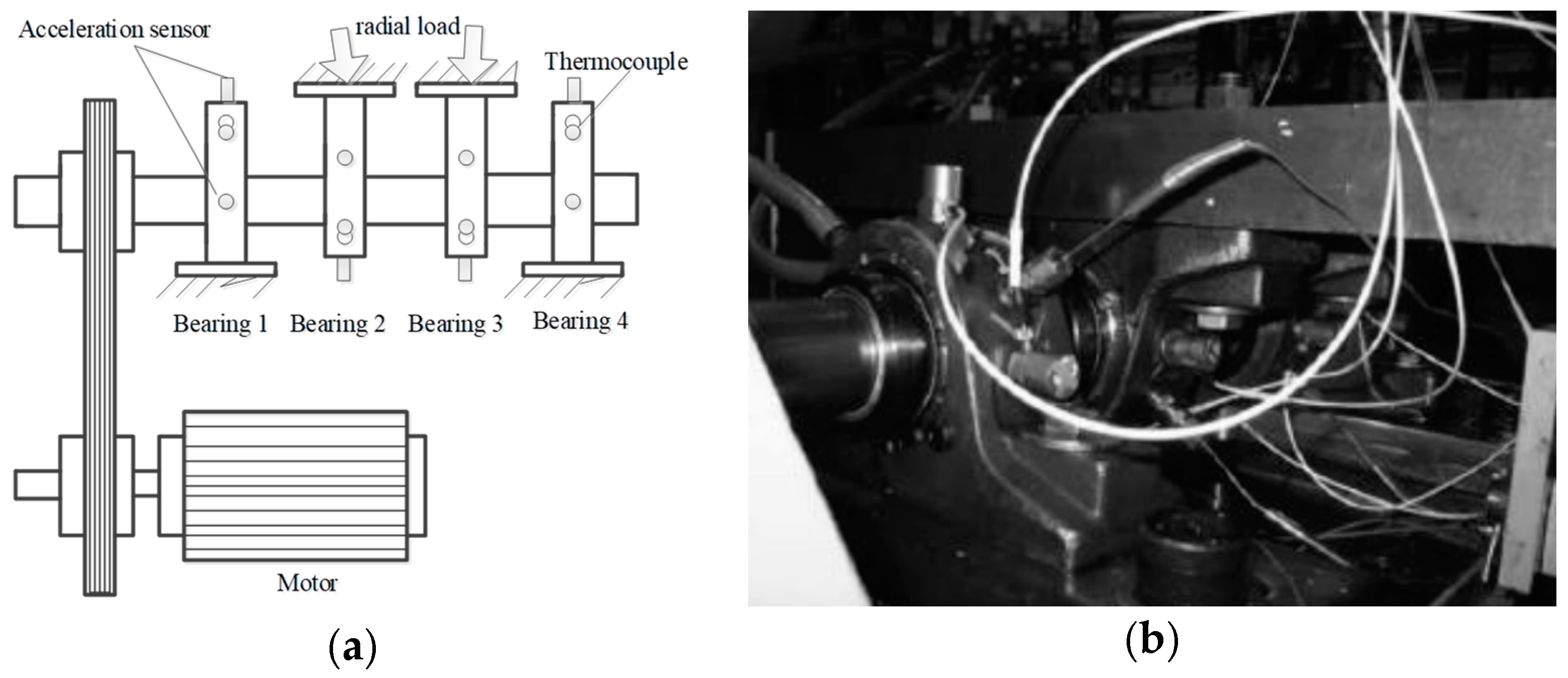
The Intelligent Maintenance Systems of Cincinnati is shown in
Figure 7. Four Rexnord ZA-2115 double row bearings were installed on a shaft, which was driven by an AC motor at the speed of 2000 RPM via sever rub belts. Each row of the bearing has
roller elements. The circle diameter of the bearing bitch and roller elements are respectively
,
, and the bearing’s contact angle is
= 15.17°. They utilized high sensitivity quartz ICP accelerometers (PCB 353B33), installed on the bearing housing, collecting the vibration signals and NI DAQ Card 6062E collecting the signals.
We take their experimental data of fourth channel in Set No. 3 to verify our method. The total number of the time series data is 20,480, and the sampling frequency is 20 KHz. Finally, the bearing failed because of outer race fault. The rotation frequency and outer ring fault frequency can be respectively calculated as
by formulas [
42].
The time domain and the frequency domain of the selected signals are shown in
Figure 8. Obviously, it is hard to identify whether there is a bearing fault from
Figure 8b for such large amounts of interference frequency presented in the frequency spectrum.
Then we apply our algorithm on the chosen signal with chosen parameters
. The truncation rank is calculated as 484 by applying non-convex optimization regularization on the rank function. The same number of single-frequency DMD modes are obtained correspondingly. The MPE values corresponding to each DMD modes are shown in
Figure 9. We recover the wanted signals by DMD modes whose MPE values are less than 0.7. Spectrums are obtained by performing FT on the reconstruction signal, as shown in
Figure 10.
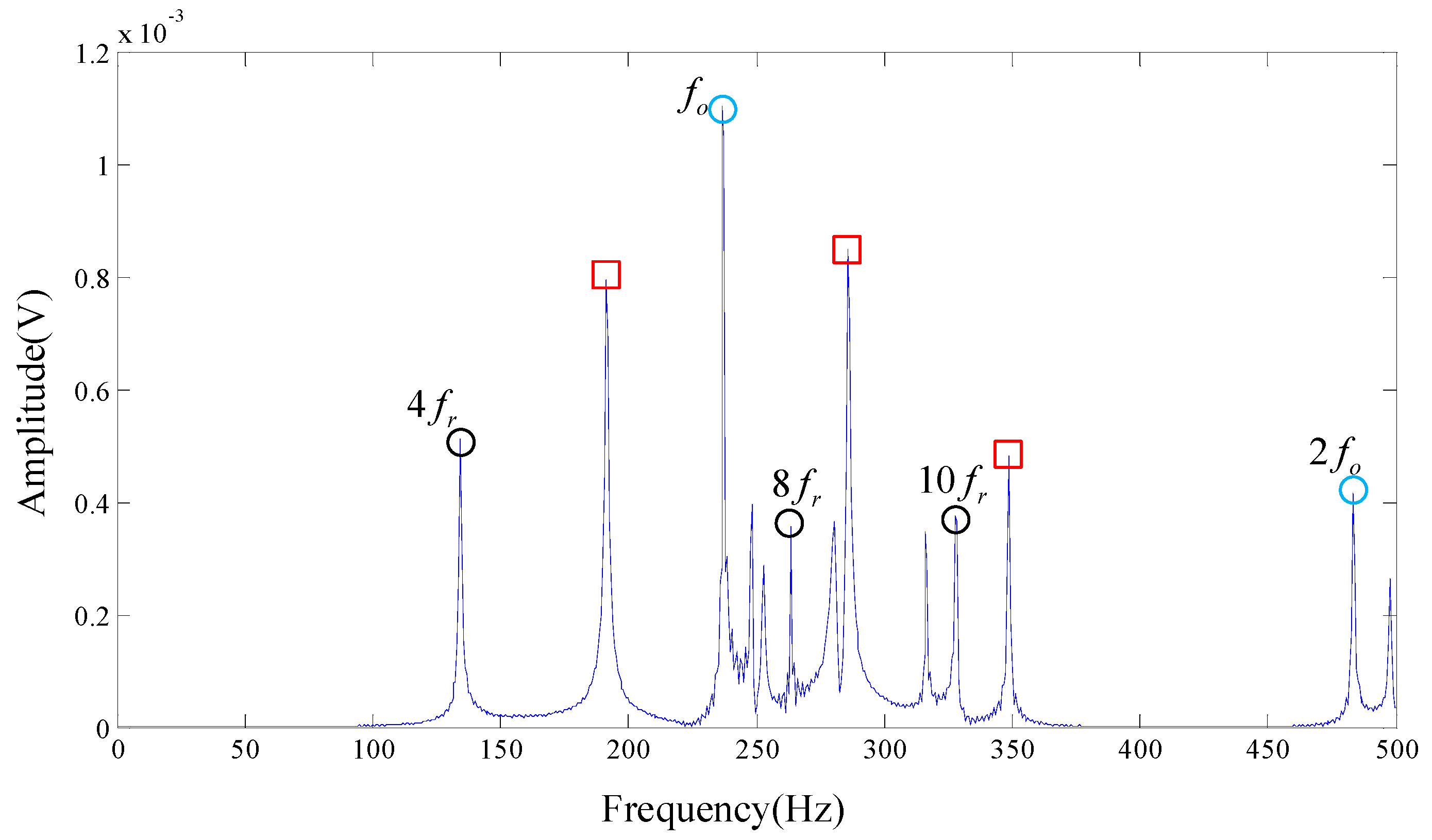
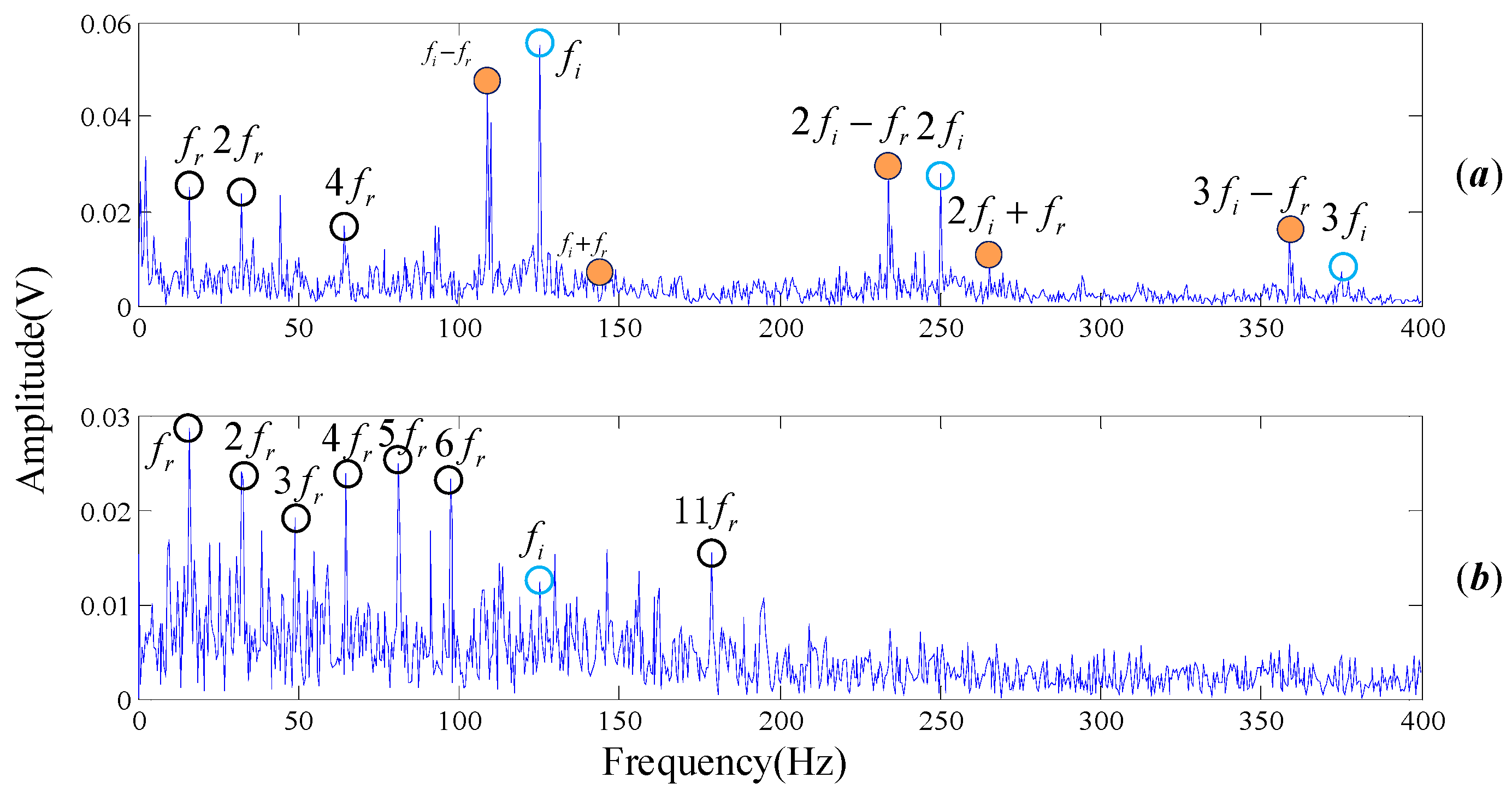
As shown in
Figure 10 there are a few characteristic frequencies located in the frequency spectrogram provided by our algorithm. Outer race failure frequency
and its resonant frequency
can be easily captured. Also, some resonant frequencies of the rotation frequency
are presented in the spectrum. However, regrettably, some of the frequencies we cannot account for are still in
Figure 10, which are shown in the red box, revealing that the signal of the actual bearing system is complex. Yet we still got the failure frequency of the bearing test signal, which is in line with experimental results.
Wavelet packet decomposition and EEMD are applied on the experimental signal, as shown in
Figure 11.
Figure 11a is the spectrum of the recover signal transformed by wavelet packet, with db15 and the default threshold. The optimal amplitude of the noise is set as 0.2 and the ensemble size is 100 for the EEMD.
Figure 11b shows the spectrum of IMF3 which has the largest correlation with the original signal. A large amount of unexplainable interference frequencies, visible in the spectrogram, seriously affect the recognition of the rotation frequency and outer ring fault frequency. Thus, the optimized DMD outperforms wavelet packet decomposition and EEMD in the mode decomposition of rolling bearing experimental signal.
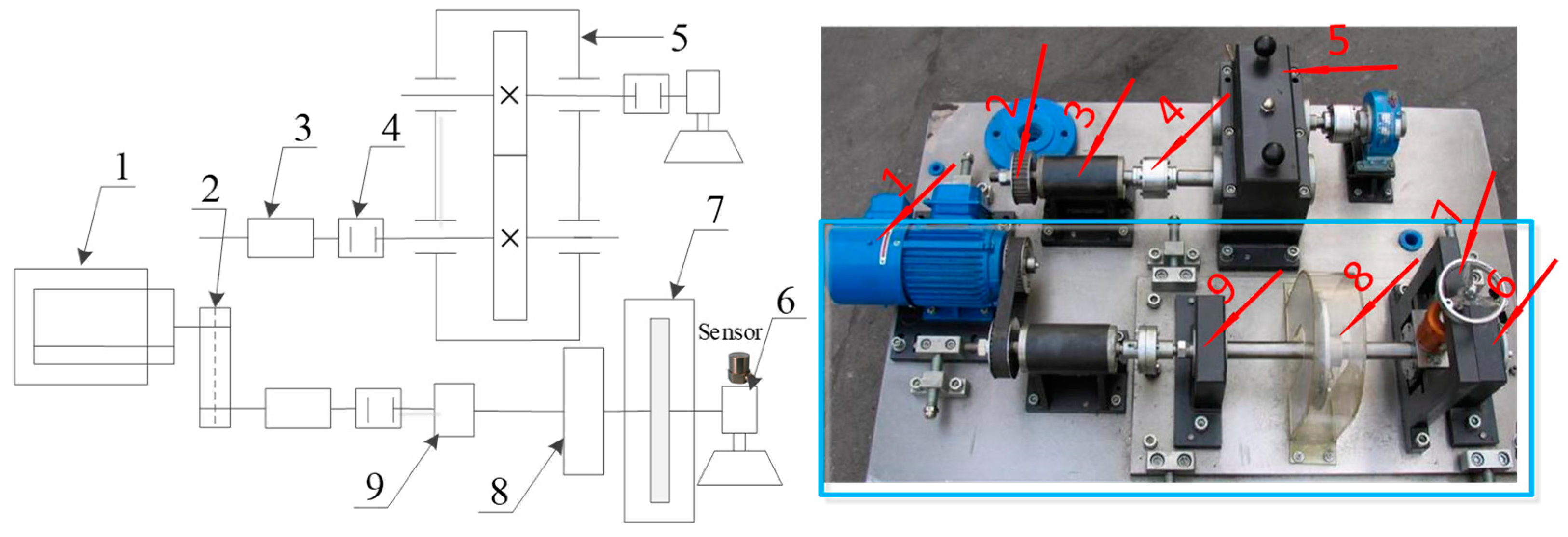
Next, we apply the algorithm on the experimental signal measured by our rotating machinery vibration analysis test rig. The physical structure of the experimental rig is shown in
Figure 12. The whole device consists of a variable speed drive motor, shaft, gear box, deflection wheel, bearing and governor. A picture of the sensor in
Figure 12 refers to the position where the single channel vibration acceleration sensor (PCB-352C33, NY, USA) is installed. A cylinder roller bearing NU205 with artificial defects on the outside surface of the inner race was mounted in the housing. The fault bearing physical diagram is shown in
Figure 13. The number of rolling elements is
, and the cylinder roller diameter is
, pitch diameter of the testing bearing is
. We set the motor at the speed of 980 RPM. So, rotation frequency and outer ring fault frequency can be calculated as
, respectively [
42].
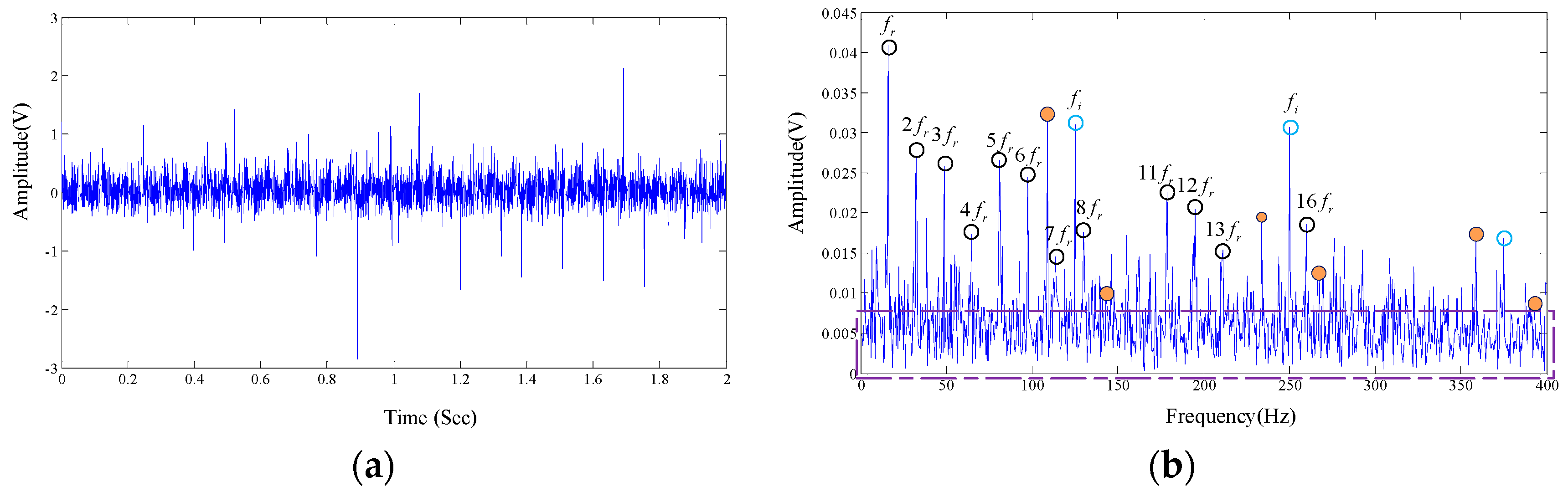
A total number of 4000 sample points, shown in
Figure 14a in time domain, are taken into analysis with the proposed algorithm. The frequency domain is shown in
Figure 14b.
As is shown in
Figure 14b, rotational frequency and its resonant frequencies are presented in the spectrum diagram. The center frequency of the inner race can also be easily found out, but the modulation components are not obvious. Meanwhile, there are large amounts of interference frequency presented in the frequency spectral. The spectrum of the test signal is not intuitionistic, which makes it difficult to diagnose the fault in view of the technicians.
Subsequently, the proposed algorithm is applied to the tested signal with the same parameters
. 682 single-frequency DMD modes are obtained by sparse optimization algorithm.
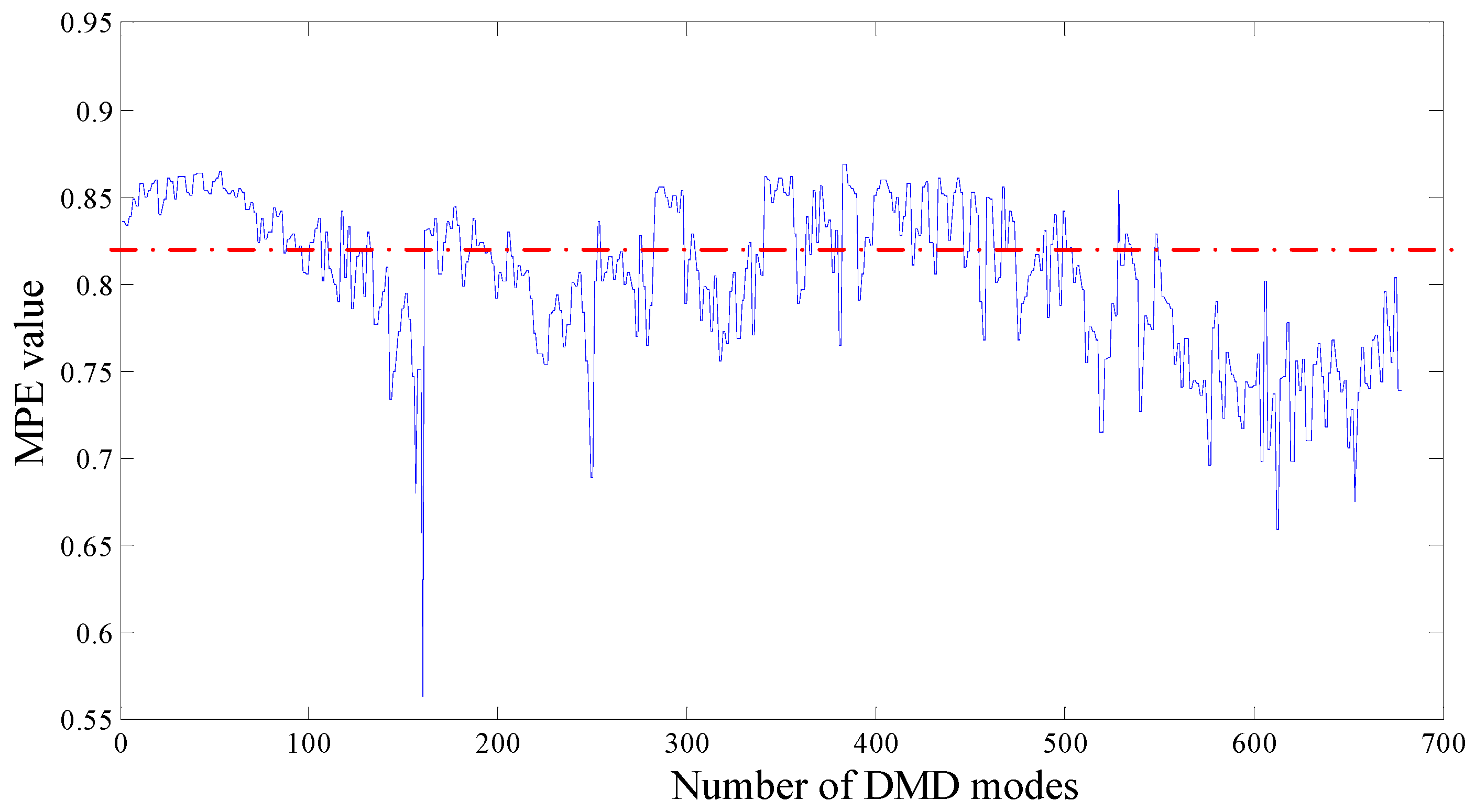
Figure 15 shows the MPE values of each DMD modes. DMD modes whose MPE values are less than 0.82 are reconstructed to form a recovery signal. Spectrums are obtained by performing FT on the reconstruction signal, as shown in
Figure 16.
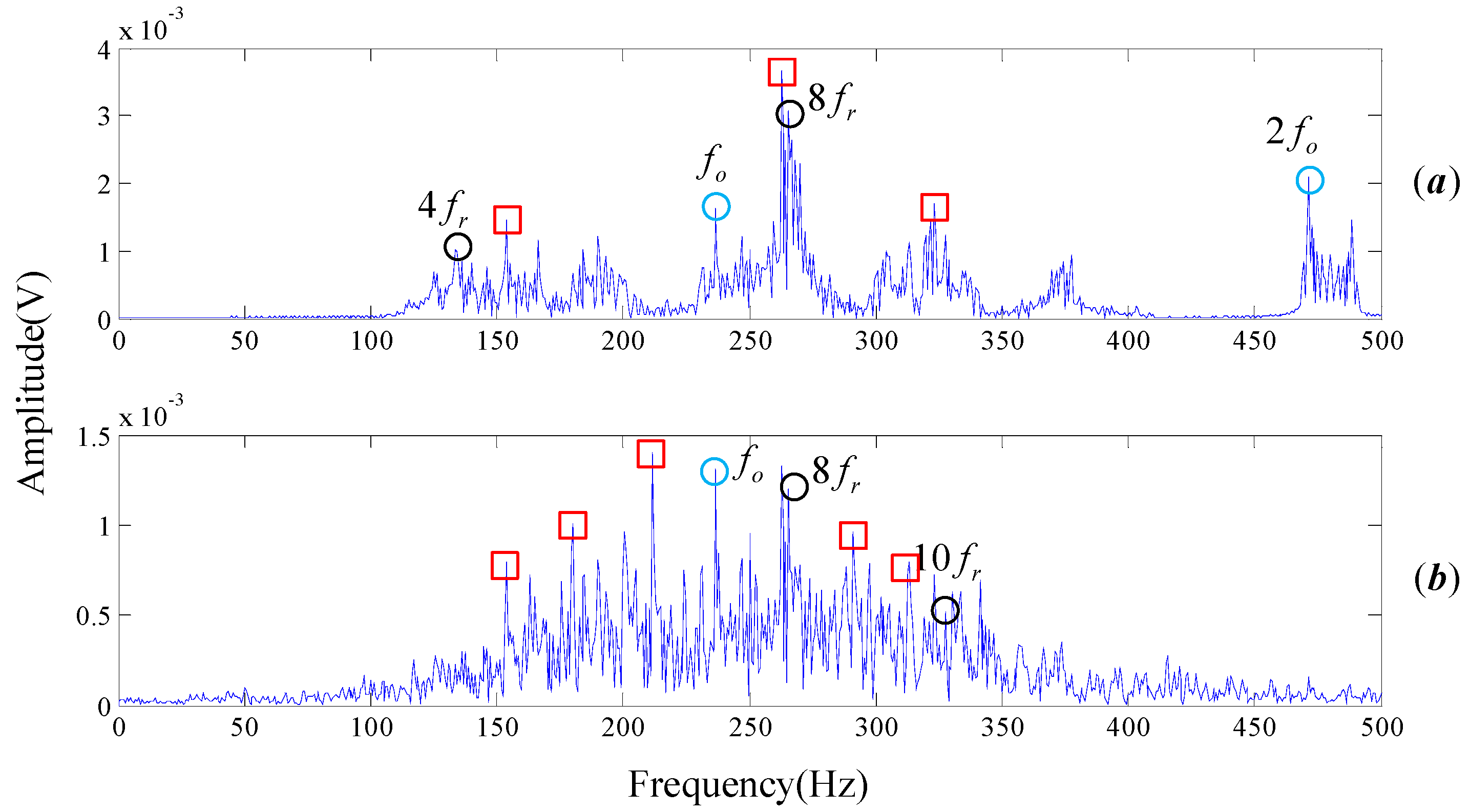
Wavelet packet decomposition and EEMD are also employed on our experimental signal, as shown in
Figure 17. The methods and parameters used in the analysis are consistent with the signal processing procedure of Cincinnati. Here the spectrum of IMF1 decomposed by EEMD is selected because it has the largest correlation with the original signal, as shown in
Figure 17b. Obviously,
Figure 16 is more readable than
Figure 13b and
Figure 17. The rotational frequency
and its harmonics (
,
,
,
) are easily identified. Not only could the center frequency be pointed out clearly but also the modulation frequency of the inner face. That is to say, we are more confident to judge that the inner race of the testing rolling bearing has encountered failure, which is highly consistent with the actual situation. The basic reason the frequencies are easy to read is that there are a few interference frequencies nearby them. Therefore, the proposed algorithm of noise reduction and feature extraction is proved to be practical and to outperform other mode decompositions such as wavelet packet decomposition and EEMD.
5. Conclusions
As a powerful tool for Koopman spectrum analysis technology with the characteristic of equation-free and data driven, DMD decomposes the time series into a series of single-frequency modes without any assumption. Theoretically, dynamic features of the original system including fault features and noise components exist in these DMD modes only if the truncation rank order r is appropriate. The truncated rank order needs to be preset artificially in the standard DMD algorithm, which is a crucial problem. Another puzzle with the application of standard DMD is of how to define a selection strategy to filter the undesired DMD modes in the process of signal reconstruction.
By proposing solutions for the selection strategy of truncated rank order and DMD modes, this paper puts forward a novel denoising and feature extraction algorithm for multi-component coupled noisy mechanical signals. Non-convex penalty regularization is adopted to the rank function of the shift-stack matrix, and a series of optimal DMD modes are obtained by this sparse optimization method. MPE is performed as a tool of optimal mode selection. After calculating the MPE of each DMD mode, signal is reconstructed by the modes whose entropies are smaller than a threshold. The proposed algorithm is successfully applied in rolling bearing simulation and experimental signals, demonstrating that it has a good application prospect in noise reduction and fault feature extraction.
DMD algorithm has been widely used in the field of fluid mechanics and video processing. This paper presents an optimized DMD algorithm and applies it to mechanical vibration signal. The parameters of non-convex penalty regularization and MPE in our algorithm are proved to be appropriate by repeated verification. The non-convex optimization method is used to extract the dynamic characteristics of the original system more comprehensively than selecting truncation rank with a “elbow” of the singular value. The dynamic characteristics, fault features and noise components of the original signal can be identified by using MPE method. However, for filtering the noise components, entropy threshold needs to be set by multiple attempts in our algorithm. For example, when dealing with the experimental signal of Cincinnati, we firstly set the threshold values of 0.7, 0.75, 0.8, etc., and then observed the effect of the recovery signal through the spectrum diagram respectively. We found that when the threshold value was 0.7, the fault characteristics were more obvious, and the interference frequencies were less. Therefore, 0.7 was selected as the criterion. Research on different vibration signals, various transmission systems and different degrees of fault damage to select a certain MPE threshold is our future work.