Computational Information Geometry for Binary Classification of High-Dimensional Random Tensors †
Abstract
:1. Introduction
1.1. State-of-the-Art and Problem Statement
1.2. Paper Organisation
2. Algebra of Tensors and Random Matrix Theory (RMT)
2.1. Multilinear Functions
2.1.1. Preliminary Definitions
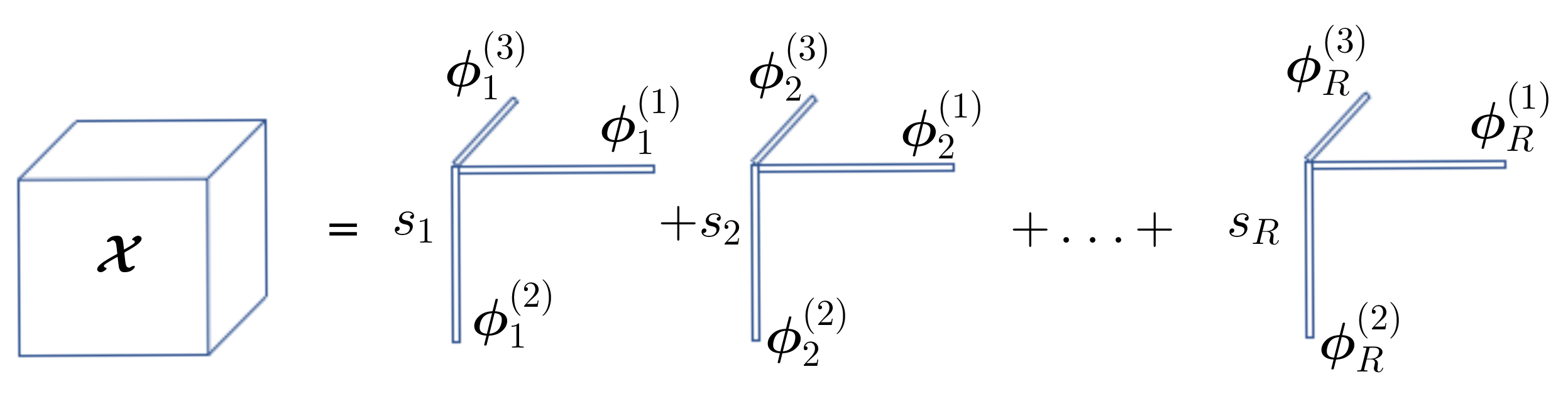
2.1.2. Canonical Polyadic Decomposition (CPD)
2.1.3. Tucker Decomposition (TKD)
2.2. The Marchenko-Pastur Distribution
3. Classification in a Computational Information Geometry (CIG) Framework
3.1. Formulation Based on a -Type Criterion
3.2. The Expected Log-likelihood Ratio in Geometry Perspective
3.3. CUB
3.4. Fisher Information
4. Computational Information Geometry for Classification
4.1. Formulation of the Observation Vector as a Structured Linear Model
- When tensor follows a Q-order CPD with a canonical rank of M, we havewhere is a structured matrix and where , i.i.d. and .
- When tensor follows a Q-order TKD of multilinear rank of , we havewhere is a structured matrix with and is the vectorization of tensor where , i.i.d.
4.2. The CPD Case
4.2.1. Small Deviation Scenario
4.2.2. Large Deviation Scenario
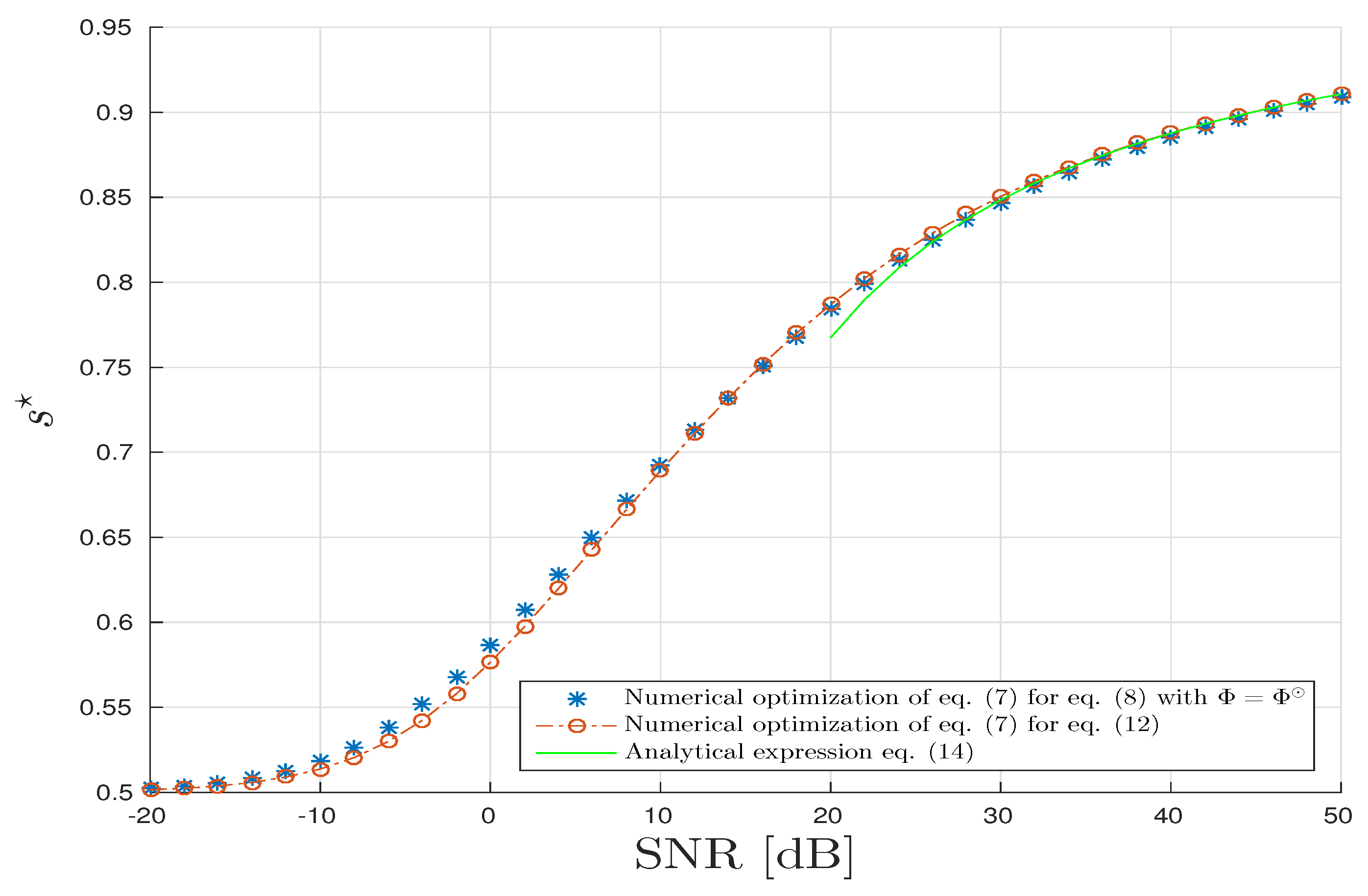
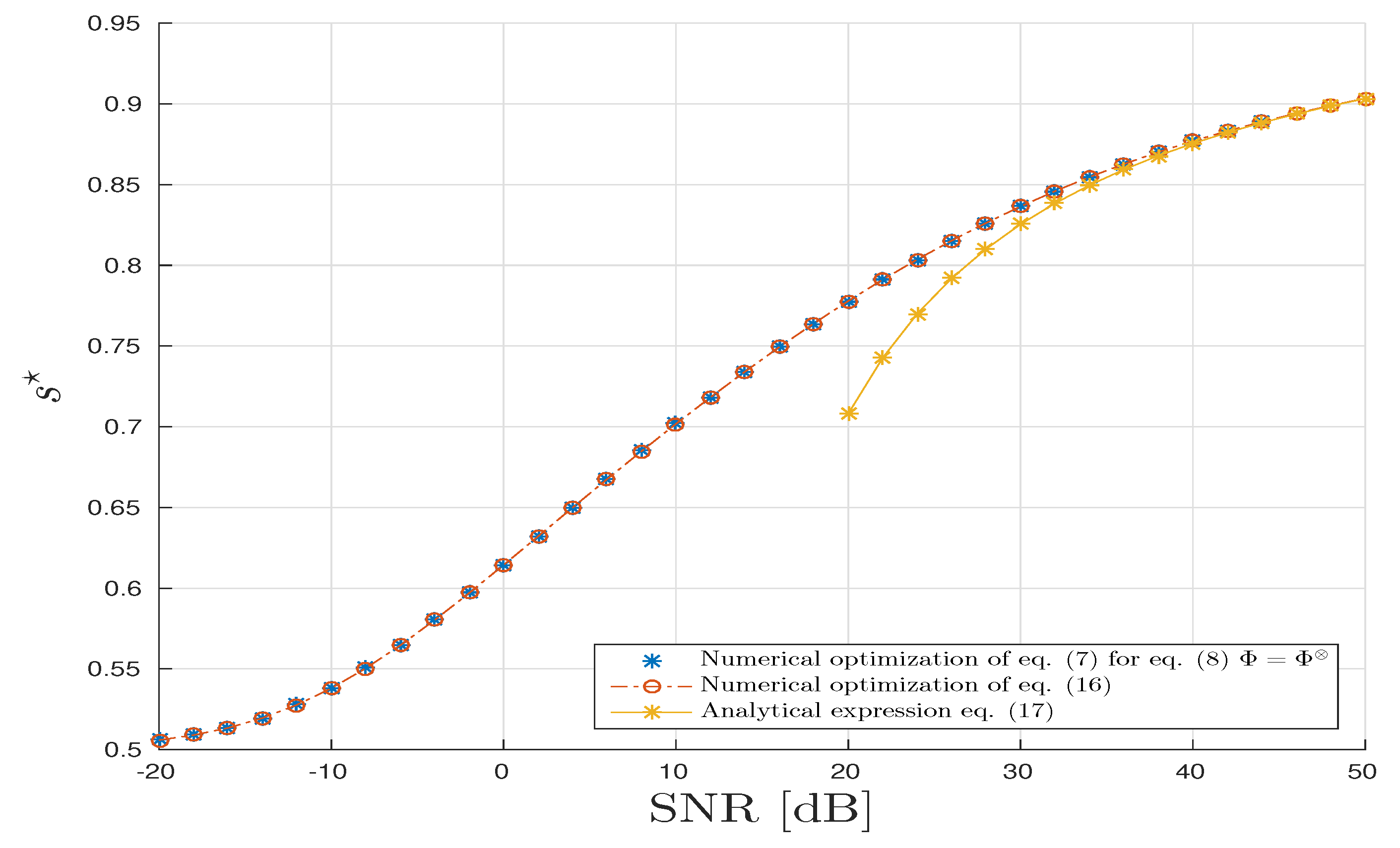
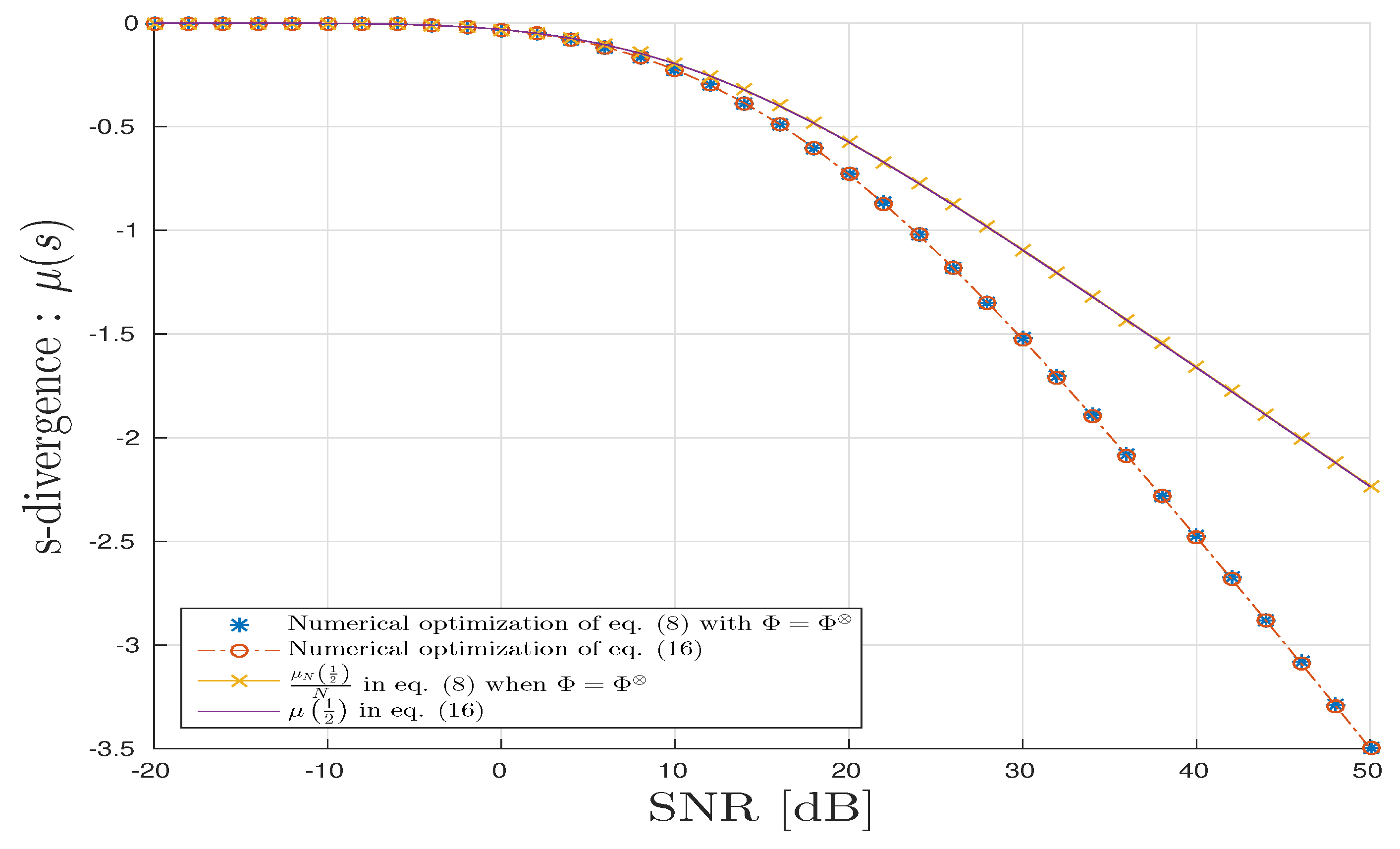
4.2.3. Approximated Analytical Expressions for and Any
- At low , we denote by , the error exponent associated with the tightest CUB, coincides with the error exponent associated with the BUB. To see this, when , we derive the second-order approximation of the optimal value in Equation (47)Result 1 and the above approximation allow us to get the best error exponent at low and ,
- Contrarily, when , . As a consequence, the optimal error exponent in this regime is not the BUB anymore. Assuming that , Equation (15) in Result 4 provides the following approximation of the optimal error exponent for large
4.3. The TKD Case
4.3.1. Large Deviation Scenario
4.3.2. Small Deviation Scenario
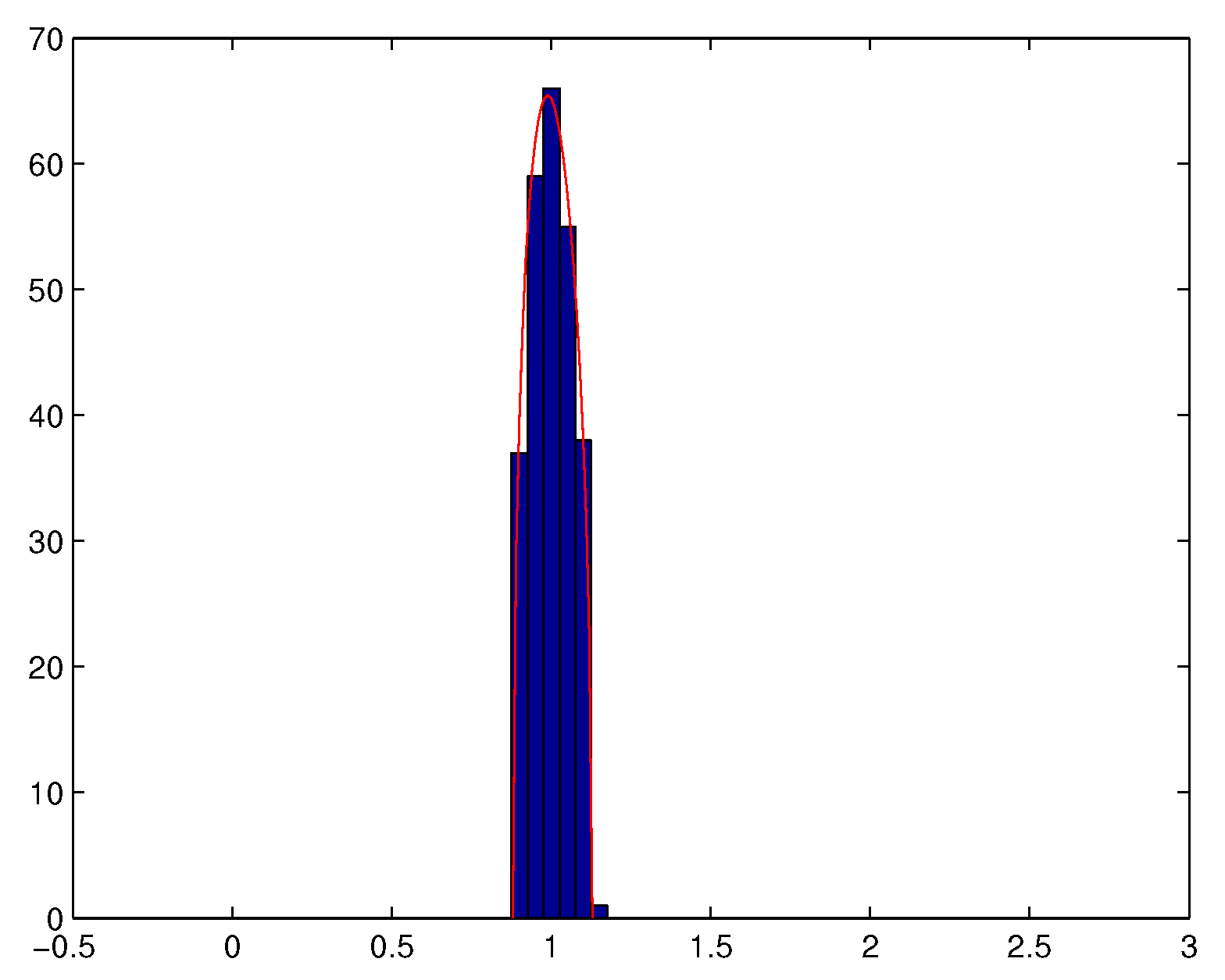
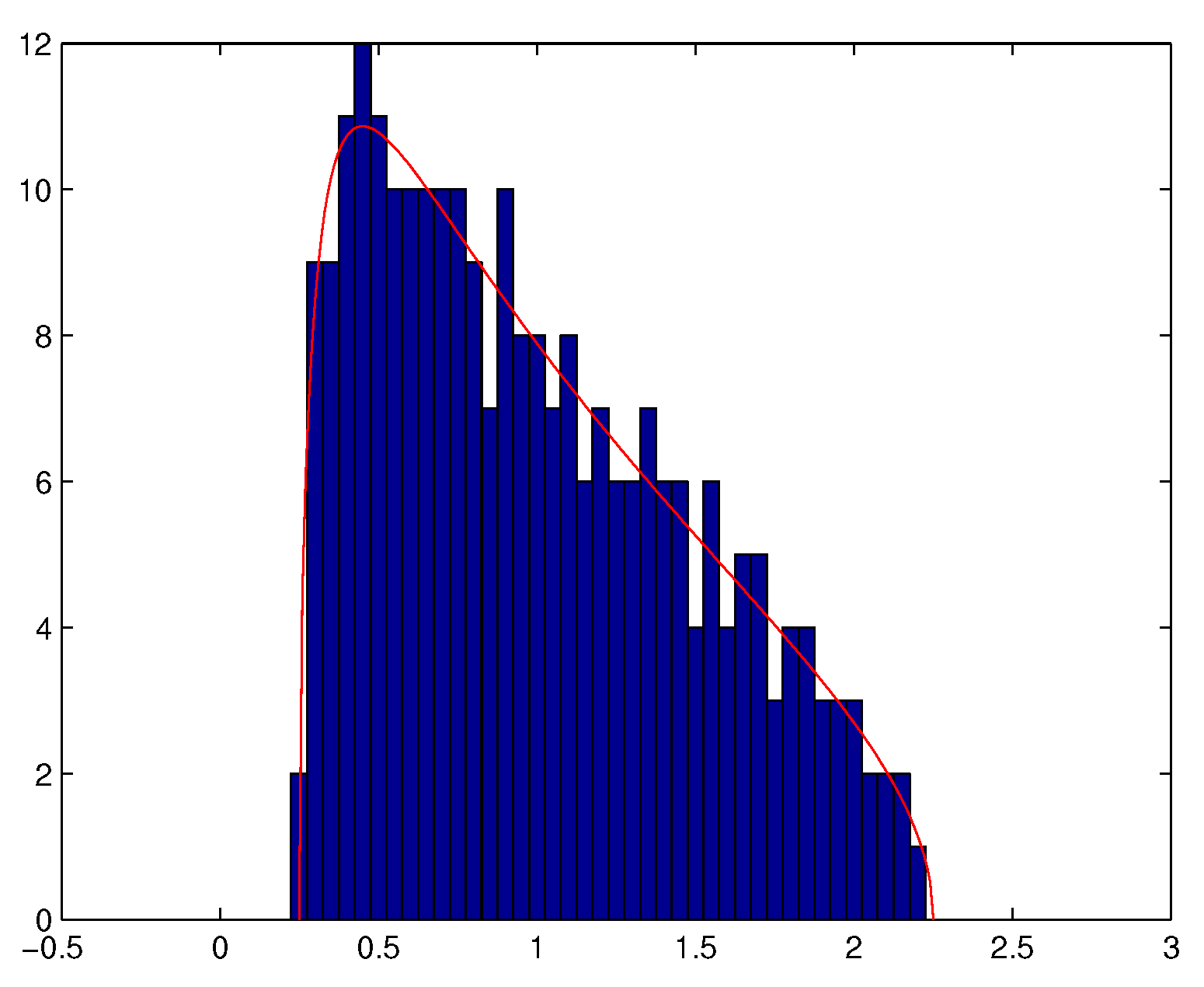
5. Numerical Illustrations
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Proof of Lemma 1
Appendix B. Proof of Lemma 2
Appendix C. Proof of Theorem 3
Appendix D. Proof of Result 1
Appendix E. Proof of Result 4
Appendix F. Proof of Result 5
References
- Besson, O.; Scharf, L.L. CFAR matched direction detector. IEEE Trans. Signal Process. 2006, 54, 2840–2844. [Google Scholar] [CrossRef]
- Bianchi, P.; Debbah, M.; Maida, M.; Najim, J. Performance of Statistical Tests for Source Detection using Random Matrix Theory. IEEE Trans. Inf. Theory 2011, 57, 2400–2419. [Google Scholar] [CrossRef] [Green Version]
- Kay, S.M. Fundamentals of Statistical Signal Processing, Volume II: Detection Theory; PTR Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Loubaton, P.; Vallet, P. Almost Sure Localization of the Eigenvalues in a Gaussian Information Plus Noise Model. Application to the Spiked Models. Electron. J. Probab. 2011, 16, 1934–1959. [Google Scholar] [CrossRef]
- Mestre, X. Improved Estimation of Eigenvalues and Eigenvectors of Covariance Matrices Using Their Sample Estimates. IEEE Trans. Inf. Theory 2008, 54, 5113–5129. [Google Scholar] [CrossRef]
- Baik, J.; Silverstein, J. Eigenvalues of large sample covariance matrices of spiked population models. J. Multivar. Anal. 2006, 97, 1382–1408. [Google Scholar] [CrossRef]
- Silverstein, J.W.; Combettes, P.L. Signal detection via spectral theory of large dimensional random matrices. IEEE Trans. Signal Process. 1992, 40, 2100–2105. [Google Scholar] [CrossRef]
- Cheng, Y.; Hua, X.; Wang, H.; Qin, Y.; Li, X. The Geometry of Signal Detection with Applications to Radar Signal Processing. Entropy 2016, 18, 381. [Google Scholar] [CrossRef]
- Ali, S.M.; Silvey, S.D. A General Class of Coefficients of Divergence of One Distribution from Another. J. R. Stat. Soc. Ser. B (Methodol.) 1966, 28, 131–142. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Kailath, T. The Divergence and Bhattacharyya Distance Measures in Signal Selection. IEEE Trans. Commun. Technol. 1967, 15, 52–60. [Google Scholar]
- Nielsen, F. Hypothesis Testing, Information Divergence and Computational Geometry; Geometric Science of Information; Springer: Berlin, Germany, 2013; pp. 241–248. [Google Scholar]
- Sinanovic, S.; Johnson, D.H. Toward a theory of information processing. Signal Process. 2007, 87, 1326–1344. [Google Scholar] [CrossRef]
- Chernoff, H. A Measure of Asymptotic Efficiency for Tests of a Hypothesis Based on the sum of Observations. Ann. Math. Stat. 1952, 23, 493–507. [Google Scholar] [CrossRef]
- Nielsen, F. Chernoff information of exponential families. arXiv, 2011; arXiv:1102.2684. [Google Scholar]
- Chepuri, S.P.; Leus, G. Sparse sensing for distributed Gaussian detection. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, Australia, 19–24 April 2015. [Google Scholar]
- Tang, G.; Nehorai, A. Performance Analysis for Sparse Support Recovery. IEEE Trans. Inf. Theory 2010, 56, 1383–1399. [Google Scholar] [CrossRef]
- Lee, Y.; Sung, Y. Generalized Chernoff Information for Mismatched Bayesian Detection and Its Application to Energy Detection. IEEE Signal Process. Lett. 2012, 19, 753–756. [Google Scholar]
- Grossi, E.; Lops, M. Space-time code design for MIMO detection based on Kullback-Leibler divergence. IEEE Trans. Inf. Theory 2012, 58, 3989–4004. [Google Scholar] [CrossRef]
- Sen, S.; Nehorai, A. Sparsity-Based Multi-Target Tracking Using OFDM Radar. IEEE Trans. Signal Process. 2011, 59, 1902–1906. [Google Scholar] [CrossRef]
- Boyer, R.; Delpha, C. Relative-entropy based beamforming for secret key transmission. In Proceedings of the 2012 IEEE 7th Sensor Array and Multichannel Signal Processing Workshop (SAM), Hoboken, NJ, USA, 17–20 June 2012. [Google Scholar]
- Tran, N.D.; Boyer, R.; Marcos, S.; Larzabal, P. Angular resolution limit for array processing: Estimation and information theory approaches. In Proceedings of the 20th European Signal Processing Conference (EUSIPCO), Bucharest, Romania, 27–31 August 2012. [Google Scholar]
- Katz, G.; Piantanida, P.; Couillet, R.; Debbah, M. Joint estimation and detection against independence. In Proceedings of the Annual Conference on Communication Control and Computing (Allerton), Monticello, IL, USA, 30 September–3 October 2014; pp. 1220–1227. [Google Scholar]
- Nielsen, F. An information-geometric characterization of Chernoff information. IEEE Signal Process. Lett. 2013, 20, 269–272. [Google Scholar] [CrossRef]
- Cichocki, A.; Mandic, D.; De Lathauwer, L.; Zhou, G.; Zhao, Q.; Caiafa, C.; Phan, H.A. Tensor decompositions for signal processing applications: From two-way to multiway component analysis. IEEE Signal Process. Mag. 2015, 32, 145–163. [Google Scholar] [CrossRef]
- Comon, P. Tensors: A brief introduction. IEEE Signal Process. Mag. 2014, 31, 44–53. [Google Scholar] [CrossRef]
- De Lathauwer, L.; Moor, B.D.; Vandewalle, J. A Multilinear Singular Value Decomposition. SIAM J. Matrix Anal. Appl. 2000, 21, 1253–1278. [Google Scholar] [CrossRef]
- Tucker, L.R. Some mathematical notes on three-mode factor analysis. Psychometrika 1966, 31, 279–311. [Google Scholar] [CrossRef] [PubMed]
- Comon, P.; Berge, J.T.; De Lathauwer, L.; Castaing, J. Generic and Typical Ranks of Multi-Way Arrays. Linear Algebra Appl. 2009, 430, 2997–3007. [Google Scholar] [CrossRef] [Green Version]
- De Lathauwer, L. A survey of tensor methods. In Proceedings of the IEEE International Symposium on Circuits and Systems, ISCAS 2009, Taipei, Taiwan, 24–27 May 2009. [Google Scholar]
- Comon, P.; Luciani, X.; De Almeida, A.L.F. Tensor decompositions, alternating least squares and other tales. J. Chemom. 2009, 23, 393–405. [Google Scholar] [CrossRef] [Green Version]
- Goulart, J.H.D.M.; Boizard, M.; Boyer, R.; Favier, G.; Comon, P. Tensor CP Decomposition with Structured Factor Matrices: Algorithms and Performance. IEEE J. Sel. Top. Signal Process. 2016, 10, 757–769. [Google Scholar] [CrossRef]
- Eckart, C.; Young, G. The approximation of one matrix by another of lower rank. Psychometrika 1936, 1, 211–218. [Google Scholar]
- Badeau, R.; Richard, G.; David, B. Fast and stable YAST algorithm for principal and minor subspace tracking. IEEE Trans. Signal Process. 2008, 56, 3437–3446. [Google Scholar] [CrossRef]
- Boyer, R.; Badeau, R. Adaptive multilinear SVD for structured tensors. In Proceedings of the 2006 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP’06), Toulouse, France, 14–19 May 2006. [Google Scholar]
- Boizard, M.; Ginolhac, G.; Pascal, F.; Forster, P. Low-rank filter and detector for multidimensional data based on an alternative unfolding HOSVD: Application to polarimetric STAP. EURASIP J. Adv. Signal Process. 2014, 2014, 119. [Google Scholar] [CrossRef]
- Bouleux, G.; Boyer, R. Sparse-Based Estimation Performance for Partially Known Overcomplete Large-Systems. Signal Process. 2017, 139, 70–74. [Google Scholar] [CrossRef]
- Boyer, R.; Couillet, R.; Fleury, B.-H.; Larzabal, P. Large-System Estimation Performance in Noisy Compressed Sensing with Random Support—A Bayesian Analysis. IEEE Trans. Signal Process. 2016, 64, 5525–5535. [Google Scholar] [CrossRef]
- Ollier, V.; Boyer, R.; El Korso, M.N.; Larzabal, P. Bayesian Lower Bounds for Dense or Sparse (Outlier) Noise in the RMT Framework. In Proceedings of the 2016 IEEE Sensor Array and Multichannel Signal Processing Workshop (SAM 16), Rio de Janerio, Brazil, 10–13 July 2016. [Google Scholar]
- Wishart, J. The generalized product moment distribution in samples. Biometrika 1928, 20A, 32–52. [Google Scholar] [CrossRef]
- Wigner, E.P. On the statistical distribution of the widths and spacings of nuclear resonance levels. Proc. Camb. Philos. Soc. 1951, 47, 790–798. [Google Scholar] [CrossRef]
- Wigner, E.P. Characteristic vectors of bordered matrices with infinite dimensions. Ann. Math. 1955, 62, 548–564. [Google Scholar]
- Bai, Z.D.; Silverstein, J.W. Spectral Analysis of Large Dimensional Random Matrices, 2nd ed.; Springer Series in Statistics; Springer: Berlin, Germany, 2010. [Google Scholar]
- Girko, V.L. Theory of Random Determinants; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1990. [Google Scholar]
- Marchenko, V.A.; Pastur, L.A. Distribution of eigenvalues for some sets of random matrices. Math. Sb. (N.S.) 1967, 72, 507–536. [Google Scholar]
- Voiculescu, D. Limit laws for random matrices and free products. Invent. Math. 1991, 104, 201–220. [Google Scholar] [CrossRef]
- Boyer, R.; Nielsen, F. Information Geometry Metric for Random Signal Detection in Large Random Sensing Systems. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017. [Google Scholar]
- Boyer, R.; Loubaton, P. Large deviation analysis of the CPD detection problem based on random tensor theory. In Proceedings of the 2017 25th European Association for Signal Processing (EUSIPCO), Kos, Greece, 28 August–2 September 2017. [Google Scholar]
- Lytova, A. Central Limit Theorem for Linear Eigenvalue Statistics for a Tensor Product Version of Sample Covariance Matrices. J. Theor. Prob. 2017, 1–34. [Google Scholar] [CrossRef]
- Tulino, A.M.; Verdu, S. Random Matrix Theory and Wireless Communications; Now Publishers Inc.: Hanover, MA, USA, 2004; Volume 1. [Google Scholar]
- Milne-Thomson, L.M. “Elliptic Integrals” (Chapter 17). In Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing; Abramowitz, M., Stegun, I.A., Eds.; Dover Publications: New York, NY, USA, 1972; pp. 587–607. [Google Scholar]
- Behrens, R.T.; Scharf, L.L. Signal processing applications of oblique projection operators. IEEE Trans. Signal Process. 1994, 42, 1413–1424. [Google Scholar] [CrossRef]
- Pajor, A.; Pastur, L.A. On the Limiting Empirical Measure of the sum of rank one matrices with log-concave distribution. Stud. Math. 2009, 195, 11–29. [Google Scholar] [CrossRef]
- Ambainis, A.; Harrow, A.W.; Hastings, M.B. Random matrix theory: Extending random matrix theory to mixtures of random product states. Commun. Math. Phys. 2012, 310, 25–74. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, G.-T.; Boyer, R.; Nielsen, F. Computational Information Geometry for Binary Classification of High-Dimensional Random Tensors. Entropy 2018, 20, 203. https://doi.org/10.3390/e20030203
Pham G-T, Boyer R, Nielsen F. Computational Information Geometry for Binary Classification of High-Dimensional Random Tensors. Entropy. 2018; 20(3):203. https://doi.org/10.3390/e20030203
Chicago/Turabian StylePham, Gia-Thuy, Rémy Boyer, and Frank Nielsen. 2018. "Computational Information Geometry for Binary Classification of High-Dimensional Random Tensors" Entropy 20, no. 3: 203. https://doi.org/10.3390/e20030203





