The adiabatic piston: a perpetuum mobile in the mesoscopic realm

Abstract

A detailed analysis of the adiabatic-piston problem reveals, for a finely-tuned choice of the spatial dimensions of the system, peculiar dynamical features that challenge the statement that an isolated system necessarily reaches a time-independent equilibrium state. In particular, the piston behaves like a perpetuum mobile, i.e., it never comes to a stop but keeps wandering, undergoing sizeable oscillations around the position corresponding to maximum entropy; this has remarkable implications on the entropy changes of a mesoscopic isolated system and on the limits of validity of the second law of thermodynamics in the mesoscopic realm.

The status of the second law of thermodynamics and the possibility that its standard interpretation may not be valid when dealing with mesoscopic regimes, in particular over temporal and spatial scales pertaining to the biological realm, has been thoroughly discussed in the First International Conference on Quantum Limits to the Second Law (San Diego, 2002) [1] A violation of the second law would have remarkable implications associated, for example, with the possibility for some living organism to extract work from a thermal bath by means of a cyclic process (perpetuum mobile). Thus, it is hardly necessary to underline the importance of being able to conceive a specific physical system which, within the limits of some reasonable hypotheses underlying its modelling, may exhibit a violation of the second law, in one of its equivalent versions. One expects this system to possess some simple universal feature if it has to be a potential candidate for supporting some ubiquitous mechanism, presently unknown, at the mesoscopic level. In this context, the quantum nature of the physical world may, or may not, play a significant role, the mesoscopic realm being the borderline between the two descriptions. In this paper we describe such a physical system, completely classical in nature (for related approaches of inherently quantum nature, see, e.g. [2]), elementary in its simplicity and yet capable of exhibiting the characteristic behaviour of a perpetuum mobile and of violating the second law. One has, however, to note that the occurrence of this remarkable result critically depends and is extremely sensitive to the linear dimensions of our system: in fact, any deviation from mesoscopic values of about 1 micron invalidates our model and its predictions.

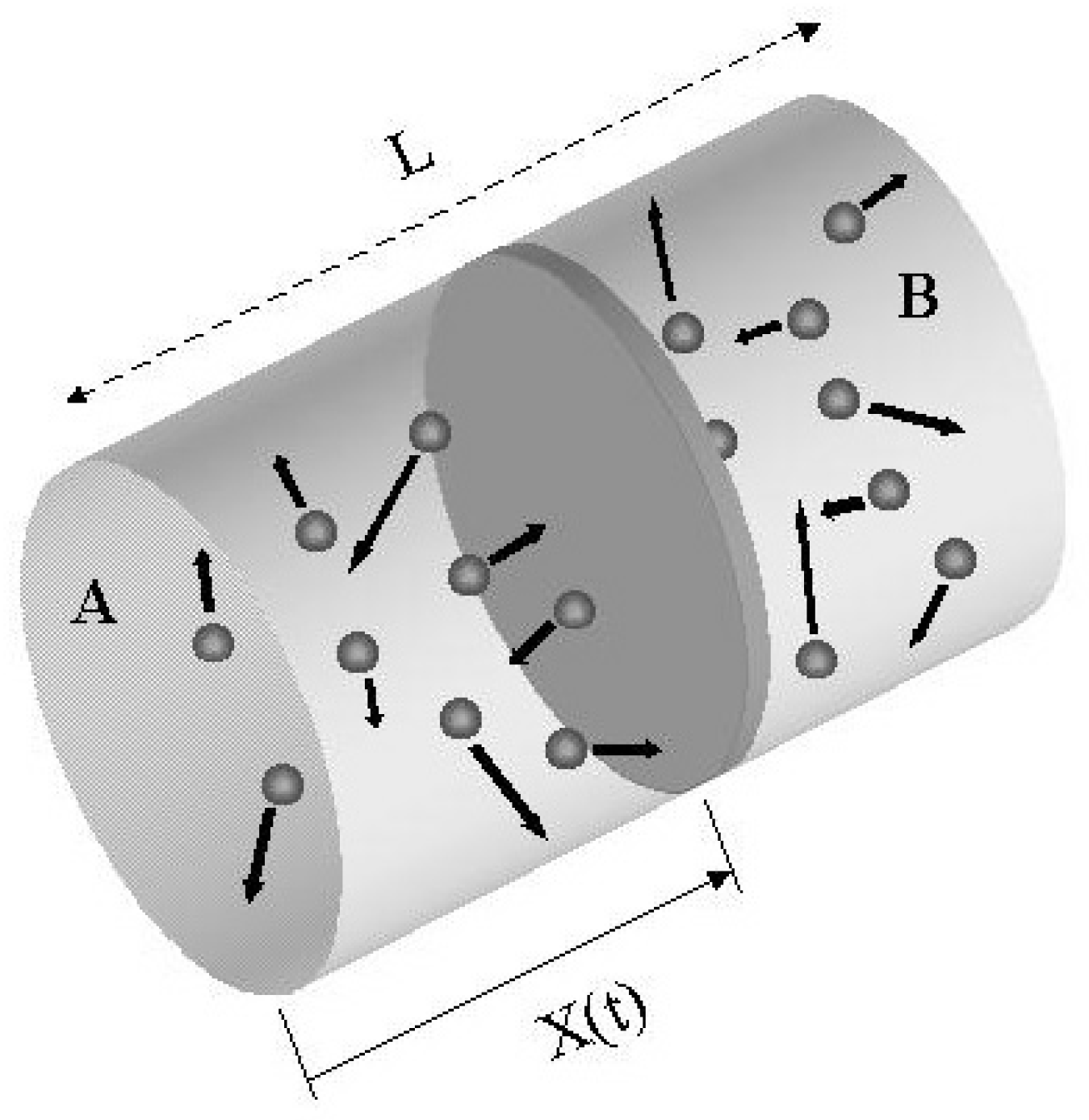
In the language of classical thermodynamics, the system consists of an isolated cylinder with rigid walls , divided into two parts by means of a frictionless adiabatic piston, each section containing the same number of moles of a perfect gas (see Fig.1). The description of its dynamical evolution towards equilibrium, when starting from an initial condition in which the pressures on the two sides are different, is not trivial: the problem (also known as the “adiabatic piston problem”) is undetermined from the point of view of elementary thermodynamics [3], and only recently a solution has been provided in the frame of an approach based on gas kinetic theory, neglecting thermodynamic fluctuations [4]. The intriguing part, however, concerns the evolution of the system, when starting from the equal-pressure equilibrium position X(t=0)=L/2 , P_A=P_B and T_A=T_B=T₀, driven by thermodynamic fluctuations, which we model by means of Langevin’s forces. In this case, as we will show below, the piston never comes to a halt but keeps moving performing sizeable random oscillations around its initial position. Actually, the system does not reach a time-independent equilibrium state and the piston behaves like a perpetuum mobile , never settling in a time independent position. The asymptotic time t_as over which these displacements occur and their amplitudes turn out to depend on the system parameters, like the ratio μ=M/M_g between the mass M of the piston and the common value M_g of the gas mass in the two sections, the length L of the cylinder and the gas temperature. In particular, under standard conditions of temperature and pressure, sizeable random displacements of the piston can be predicted for a specific range of values of L pertaining to the mesoscopic regime.

The time evolution of our system is determined by the motion of the piston, described by its instantaneous position X(t) (see Fig.1) which, in turn, obeys Newton’s equation in the presence of random elastic collisions with the gas molecules. If the system starts at time t=0 and temperature T₀, with the piston in the middle position X(t=0)=L/2 and zero velocity, then it evolves maintaining equal pressures on both sides. This last circumstance is expedient for understanding the peculiar behaviour of the piston, since, otherwise, any macroscopic pressure difference arising between the two sections would induce a restoring force which would immediately bring the piston back to its equilibrium position.

Our starting point is the deterministic equation describing the piston motion which we have derived in [5]. In order to account for the random molecular collisions, an ad hoc stochastic acceleration a(t) is formally introduced, so that the stochastic evolution equation of the piston reads

$$\frac{{\mathrm{d}}^2\mathrm{X}}{{\text{dt}}^2}+\sqrt{\frac{16{\text{nRM}}_{\mathrm{g}}{\mathrm{T}}_0}{\mathsf{\delta }{\mathrm{M}}^2\mathrm{L}}}\left(\frac{1}{\sqrt{\mathrm{X}}}+\frac{1}{\sqrt{\mathrm{L}-\mathrm{X}}}\right)\frac{\text{dX}}{\text{dt}}+\frac{{2\mathrm{M}}_{\mathrm{g}}}{\mathrm{M}}\left(\frac{\mathrm{X}-\mathrm{L}/2}{\mathrm{X}\left(\mathrm{X}-\mathrm{L}\right)}\right){\left(\frac{\text{dX}}{\text{dt}}\right)}^2=\mathrm{a}\left(\mathrm{t}\right),$$

(1)

where n is the common number of gas moles in each side and R is the gas constant. The determination of a(t) is a very complicated task since the standard Langevin approach does not in general carry over to nonlinear dynamical systems [6], as the one described by Eq.(1). In order to take advantage of the Langevin method, we linearize the above equation by considering small displacements around the starting position, that is |(X-L/2)|/(L/2)<<1, and by approximating the square of the piston velocity (dX/dt)² with its thermal velocity K_BT₀/M (both hypotheses have to be proved consistent a posteriori). Proceeding in this way, a straightforward application of the dissipation-fluctuation theorem [7] allows to deduce < a(t)a(t')>=[8(2mK_BT/π)^1/2 PS / M²]δ(t − t'), where m is the molecular mass, P the common pressure on the two sides of the piston and S its area.

The linearized form of Eq.(1) reads, after introducing the variable x=X-L/2,

$$\frac{{\mathrm{d}}^2\mathrm{X}}{{\text{dt}}^2}+\frac{8}{\text{ML}}\sqrt{\frac{{2\text{nRM}}_{\mathrm{g}}{\mathrm{T}}_0}{\mathsf{\pi }}}\frac{\text{dX}}{\text{dt}}+\frac{{8\mathrm{K}}_{\mathrm{B}}{\mathrm{M}}_{\mathrm{g}}{\mathrm{T}}_0}{{\mathrm{M}}^2{\mathrm{L}}^2}\mathrm{x}=\mathrm{a}\left(\mathrm{t}\right),$$

(2)

and is formally identical to that describing the Brownian motion of a harmonically-bound particle of mass M, a problem which has been thoroughly described in the literature [8], that is

$$\frac{{\mathrm{d}}^2\mathrm{x}}{{\text{dt}}^2}+\mathsf{\beta }\frac{\text{dx}}{\text{dt}}+{\mathsf{\omega }}^2\mathrm{x}=\mathrm{A}\left(\mathrm{t}\right),$$

(3)

where A(t) is the Langevin acceleration. Whenever β>>ω , the analysis carried out in [8] allows to identify two typical time scales t_th=1/2β and t_as=β/2ω² (t_as>>t_th), which respectively represent the thermalization time, i.e., the time over which the square-mean velocity <(dx/dt)²> attains its equipartition value K_BT₀/M and the much longer time over which, in turn, the square-mean displacement reaches its asymptotic value <x²>=K_BT₀/Mω². By comparing Eqs.(2) and (3), we can apply the results of [8] to our case, after identifying β with (8/ML)(2nRM_gT₀/π)^1/2 and ω² with 8K_BM_gT₀/M²L². In this way, we obtain t_as=(NL/u)(M/M_g)/π^1/2 and t_th=t_as/N, where N is the number of molecules of mass m in each of the two sections and u=(2K_BT₀/m) is the most probable velocity of the molecular Maxwell distribution. Therefore, since typically N>>1, t_th turns out to be much smaller than t_as, a circumstance which justifies a posteriori the substitution in Eq.(1) of (dX/dt)² with its average value K_BT₀/M. Besides, <x²>=K_BT₀/Mω²=(L/2)²M/2M_g, so that, in the limit M/M_g<<1 (that is, small piston mass with respect to gas mass), the two assumptions justifying the linearization of Eq.(1) are both verified.

The above results have relevant implications on the entropy variation of our isolated system or, more precisely, due to the stochastic nature of the problem, on the ensemble-averaged entropy change <ΔS> over many realizations of our system (starting from the initial state corresponding to the piston position X(t=0)=L/2). By recalling that during the piston motion the gas pressure remains constant on both sides, one has dS=δQ/T=c_pdT/T (c_p being the gas molar heat at constant pressure), so that, by taking advantage of the equation of state of perfect gases, the entropy change, with respect to the initial state, of a single realization of the system can be easily checked to be given by ΔS= nc_pln {[LX(t)-X²(t)]/(L/2)²}= nc_pln[(L²-4x²)/L²]. In order to get an order of magnitude for <ΔS>, we approximately write <ΔS>=nc_pln[(L²-4<x²>)/L²]. The significant quantity <ΔS>/Κ_Β turns out to be (for <x²>/(L/2)²<<1)

$$\frac{\langle \Delta \mathrm{S}\rangle }{{\mathrm{K}}_{\mathrm{B}}}=-\frac{{\mathrm{c}}_{\mathrm{p}}}{2\mathrm{R}}\mathrm{N}\frac{\mathrm{M}}{{\mathrm{M}}_{\mathrm{g}}}.$$

(4)

Accordingly, a large asymptotic entropy decrease can take place in our isolated system. The question naturally arises: what are the spatial and temporal scales over which this violation of the second law of thermodynamics can actually occur? To answer this question, we can examine the specific case of a gas (e.g.,O₂) in standard conditions: by expressing L in microns (N=3x10⁷L³) and time in seconds, we have

t_as=5x10^-2(M/M_g)L⁴,

(5)

<ΔS>/Κ_Β= −5×10⁷(M/M_g)L³

(6)

It is worthwhile to stress that the fourth-power dependence of t_as on L greatly restrict the admissible range of values of L: in fact, a variation of just one order of magnitude would make our model invalid since tas would become too large and t_th too small to justify the adiabatic and thermalization hypothesis, respectively. In other words, a violation of the second law can eventually occur, as suggested by common wisdom, only in a very limited range of the relevant parameters. As an example, for M/M_g=10^-2 and L= 1 cm we obtain an asymptotic time t_as of the order of the order of 1000 centuries! Conversely, by taking L = 1 μm, we obtain a reasonable value t_as= 5x10^-4 sec and <ΔS>/k= -5x10⁵. This corresponds to a violation of the second law in the mesoscopic realm.

The above approach has allowed us to deal with the situation (M/M_g)<<1, since only in this limit the sufficient conditions for the Langevin method [6], that is <x²>/(L/2)²=M/(2Mg)<<1, is satisfied. In order to have an insight into the behaviour of our process in the more general case M/M_g<1, we assume Langevin’s approach to continue to be approximately valid in this moderately non-linear regime. This is accomplished by using in the non-linear Eq. (1) the stochastic acceleration a(t) worked out above for the linear case.

After introducing the dimensionless units ξ=X/L and τ=t/t_p, where t_p=4√2 t_th the stochastic equation describing the piston motion reads

$$\xi +\left(\frac{1}{\sqrt{\xi }}+\frac{1}{\sqrt{1-\xi }}\right)\xi -\frac{1}{\mu }\left(\frac{1}{\xi }-\frac{1}{1-\xi }\right){\xi }^2=\sigma \alpha \left(t\right)$$

(7)

where the dot stands for derivative with respect to τ, μ=M/M_g, α(τ) a unitary-power white noise, and σ²=(π/2√2)(μ/N).

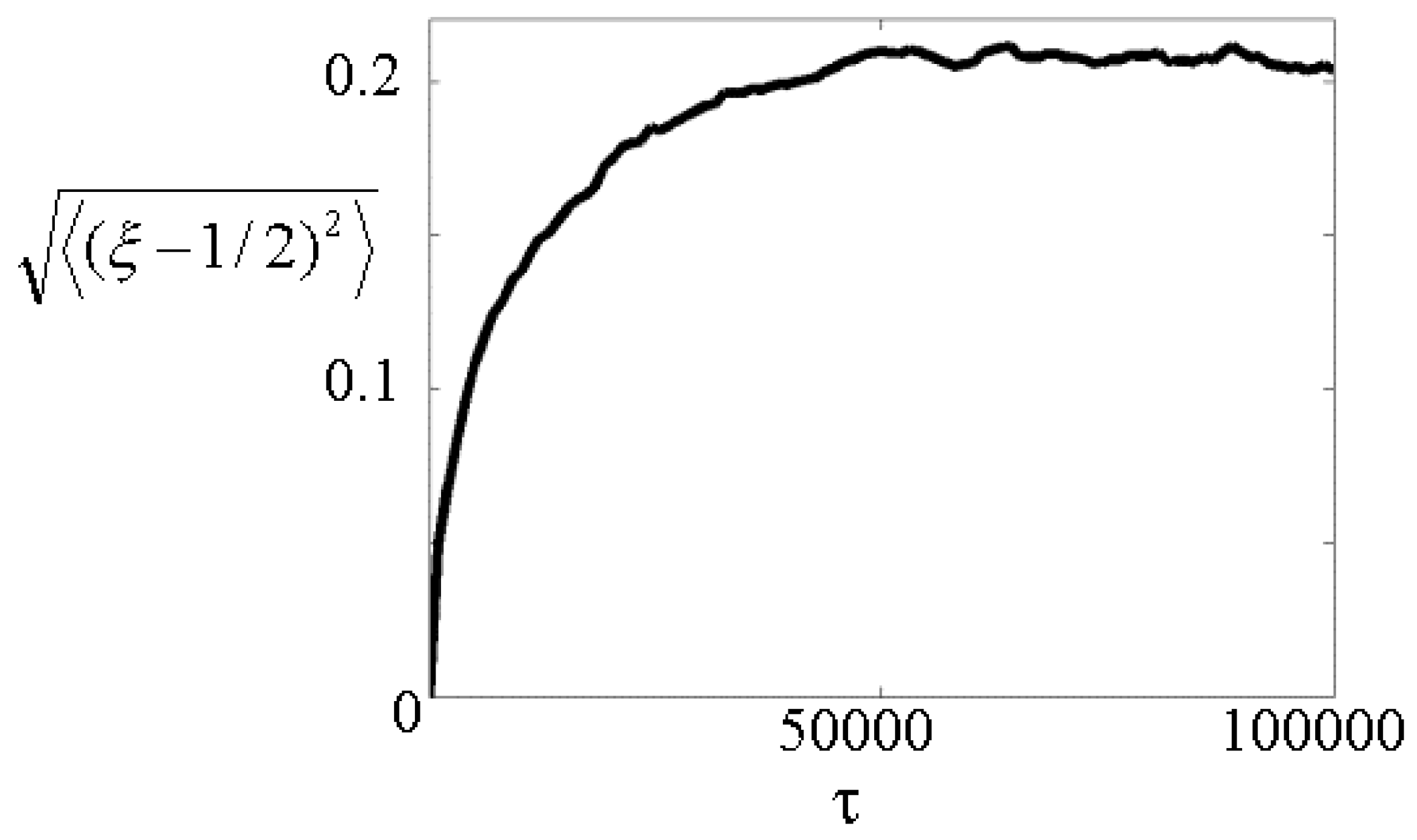
Equation (7) can be numerically integrated by adopting a second-order leap-frog algorithm as developed in [9]. In particular, this allows us to evaluate the ensemble average (over 10000 realizations of the piston) of the time evolution of the normalized mean square-root deviation <(ξ-1/2)²>^1/2 of the piston position from its initial value ξ=1/2. This analysis is reported in Fig.2 for M/M_g=0.5 and N=3x10⁴. Its inspection clearly shows that the piston undergoes random fluctuations around the central position ξ=1/2, which increase with time up to an asymptotic value corresponding to a sizeable fraction of the cylinder length.

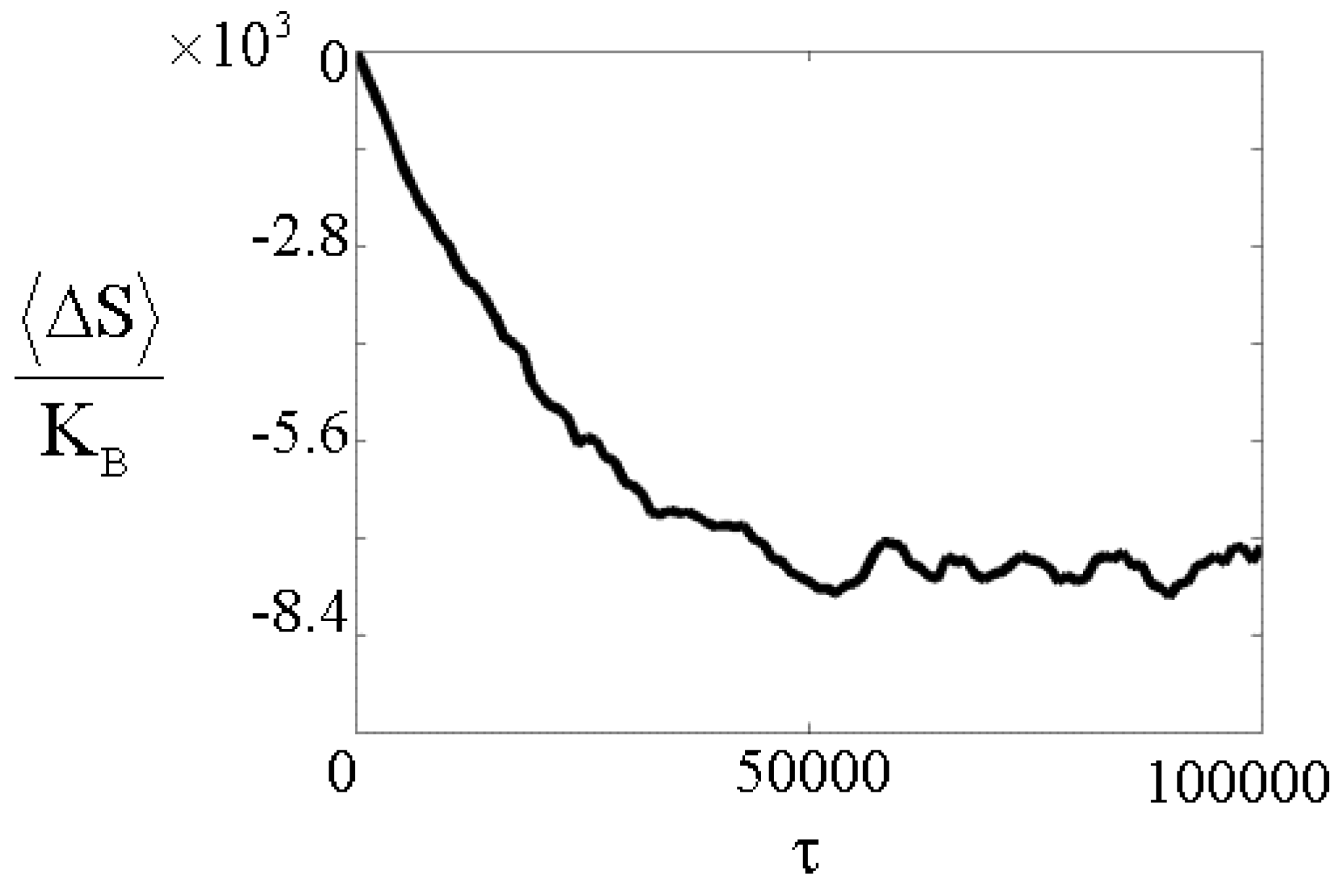
The ensemble average of the total entropy change, as given by the expression <ΔS>/K_B =N(c_p/R)<ln[(1- 4(ξ-1/2)²)>, of our isolated system can also be numerically evaluated. In Fig.3, <ΔS>/KB is reported as a function of the normalized time τ. A asymptotic entropy decrease four orders of magnitude larger than KB is present in this case. Further numerical analysis shows (see Fig.4) that, keeping N fixed and varying μ, the asymptotic value of <ΔS>/K_B undergoes an approximately linear decrease with μ, as predicted by Eq. (4). Beyond μ ≅ 0.6, the entropy decrease slows down, but we are now in a range where Langevin’s model may not be valid. Coversely, in the limit μ→0 our pproach furnishes <x²>/(L/2)²=μ/2→0 and t_as→0, consistently with the results of [10].

The above findings violate the second law in its formulation that the entropy of an isolated system cannot decrease. The celebrated Boltzmann’s H-theorem [11], which can be considered as a “proof” of the second law, does not apply in our case since one of its main hypotheses, that is the molecular-chaos assumption, is not valid in our dynamics: in fact, the correlation induced by the random motion of the piston favors a common sign of v_x and v_x’ in the two-particle correlation function of the gas near the piston, while the single-particle correlation functions are independent from the sign of v_x and v_x’. This prevents the two-particle correlation function to factorize into the product of the one-particle distribution functions.

The validity of our model basically hinges upon the existence of a nearly adiabatic piston with which the gas molecules undergo completely elastic collisions and on the assumption that the gases in the cylinder instantaneously attain an equilibrium Maxwellian distribution. Both hypotheses are justified since, a posteriori, the time t_as over which our process takes place is much larger than the time t_th=t_as/N it takes the gas to reach thermal equilibrium, and yet short enough to allow for the neglecting of heat flow through the piston and the cylinder walls.

Finally, the validity of our model appears to be corroborated by suitable molecular dynamic simulations of the evolution of our system. These typically involve a considerable number of point particles, which model the gas inside the cylinder, separated by a frictionless piston against which they undergo perfect elastic collisions. Actually, preliminary attempts in this direction [12,13] with a limited number of particles, indicates that the difference between the temperatures on the two sides [12] or, equivalently, the piston position [13] undergoes relevant oscillations, so that the system does not reach equilibrium, as predicted by our model.