Dynamic Features of the Highly Excited Vibrational States of the HOCl Non-Integrable System Based on the Dynamic Potential and Lyapunov Exponent Approaches
Abstract
:1. Introduction
2. Semi-Classical Hamiltonian of HOCl Non-Integrable System and Corresponding Dynamic Characterizing Methods
2.1. Semi-Classical Hamiltonian of HOCl Non-Integrable System
2.2. Dynamic Potential Methods for Non-Integrable System
2.3. Lyapunov Exponent—Chaotic Index of Non-Integrable Systems
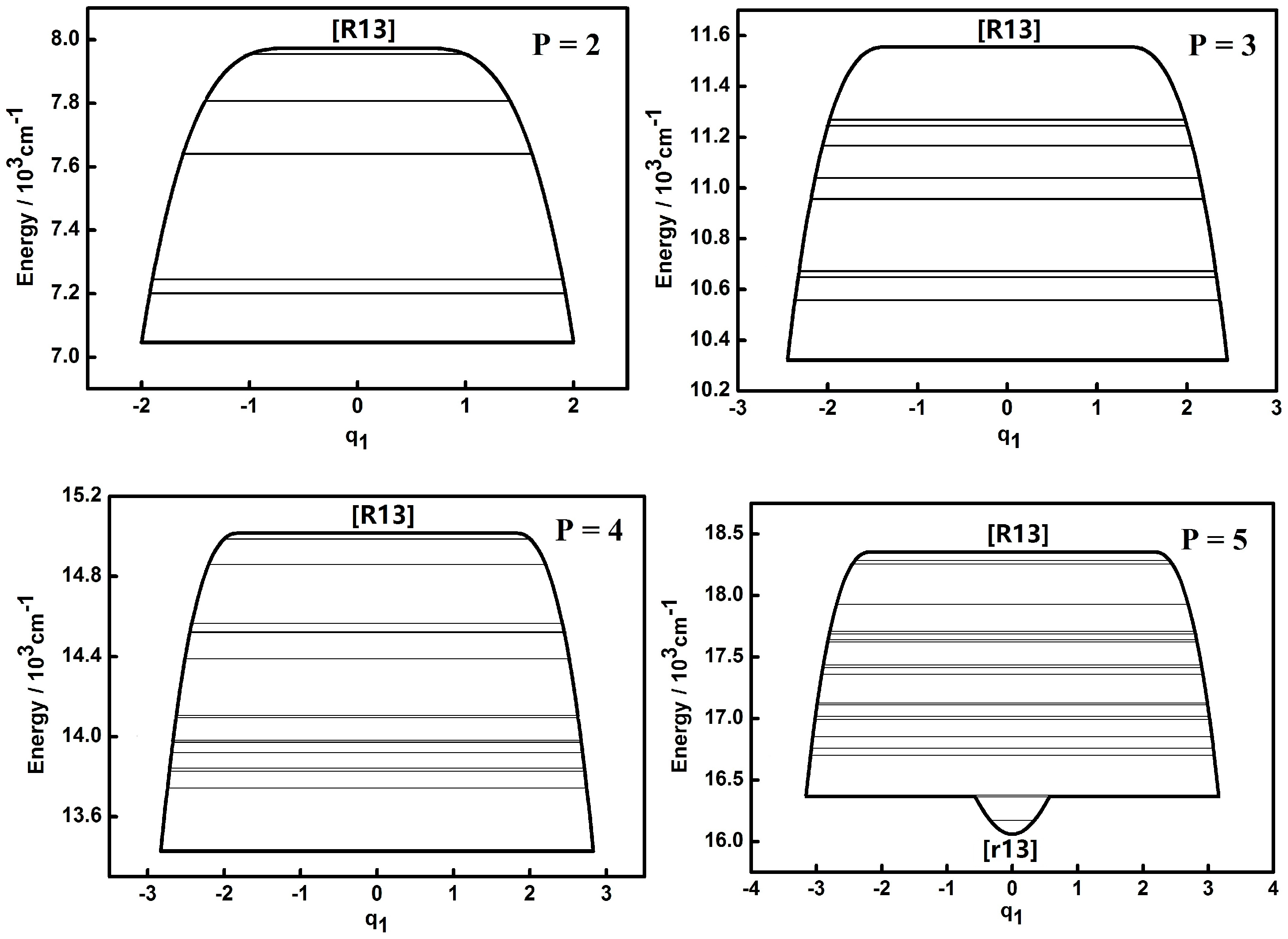
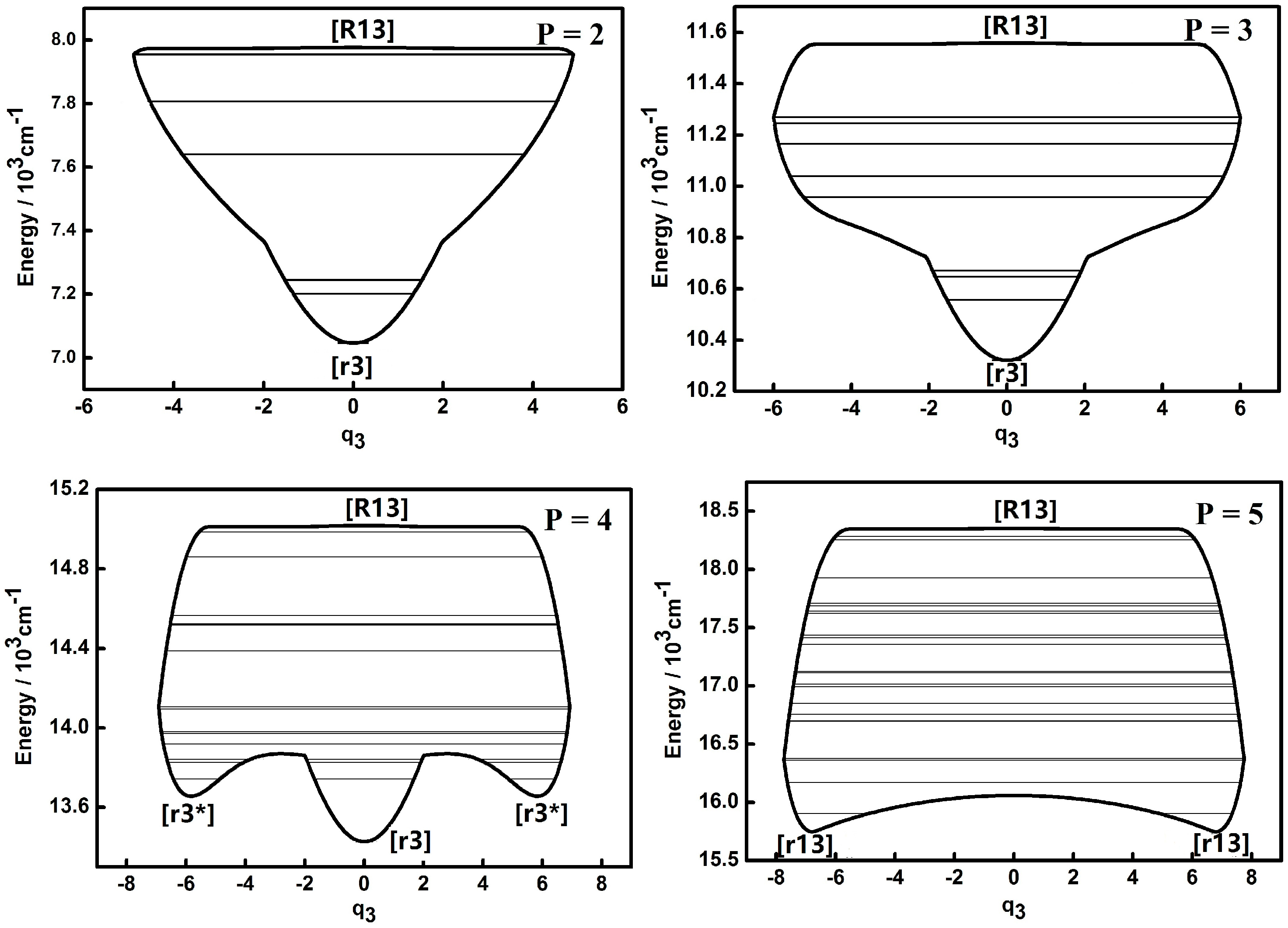
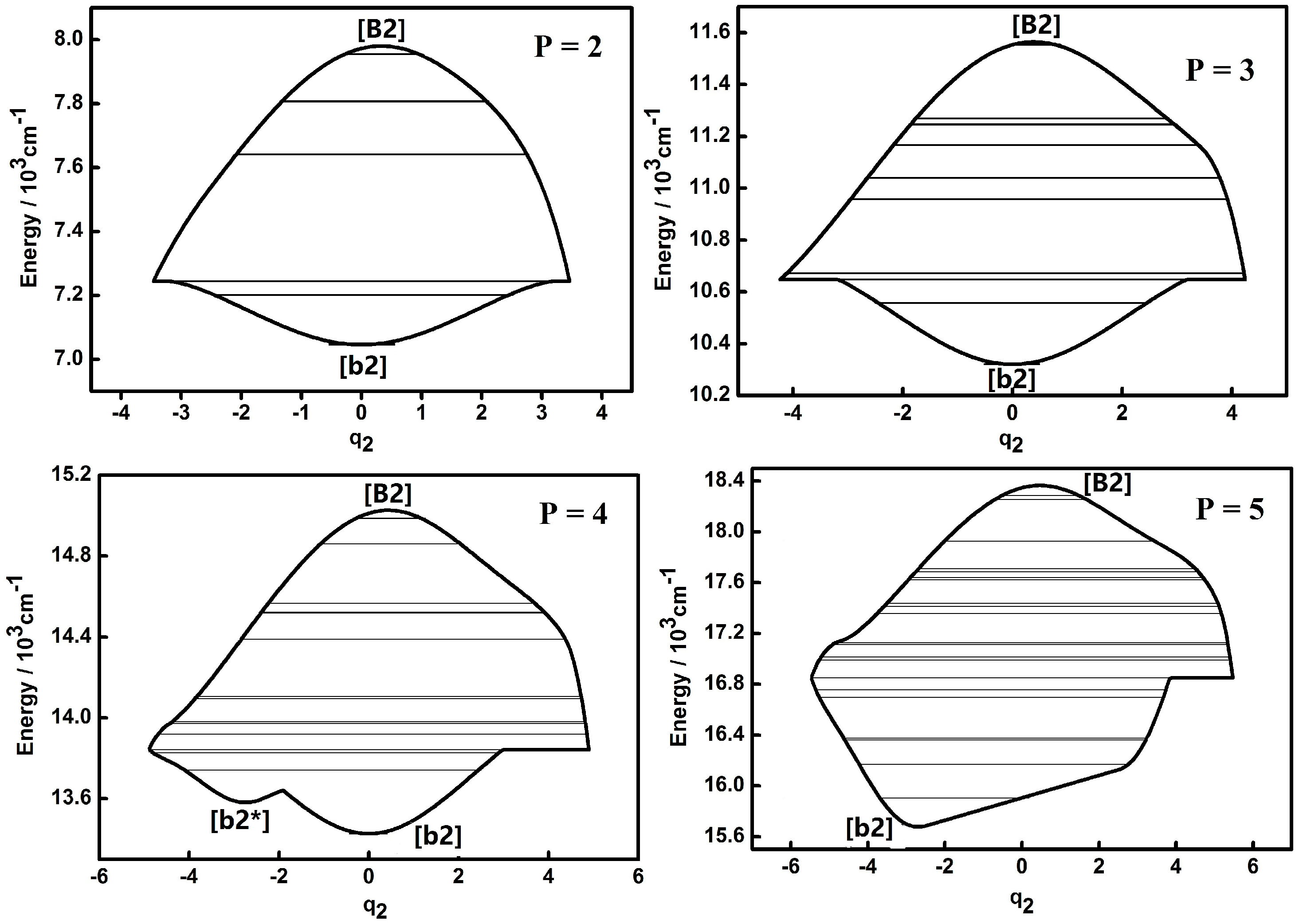
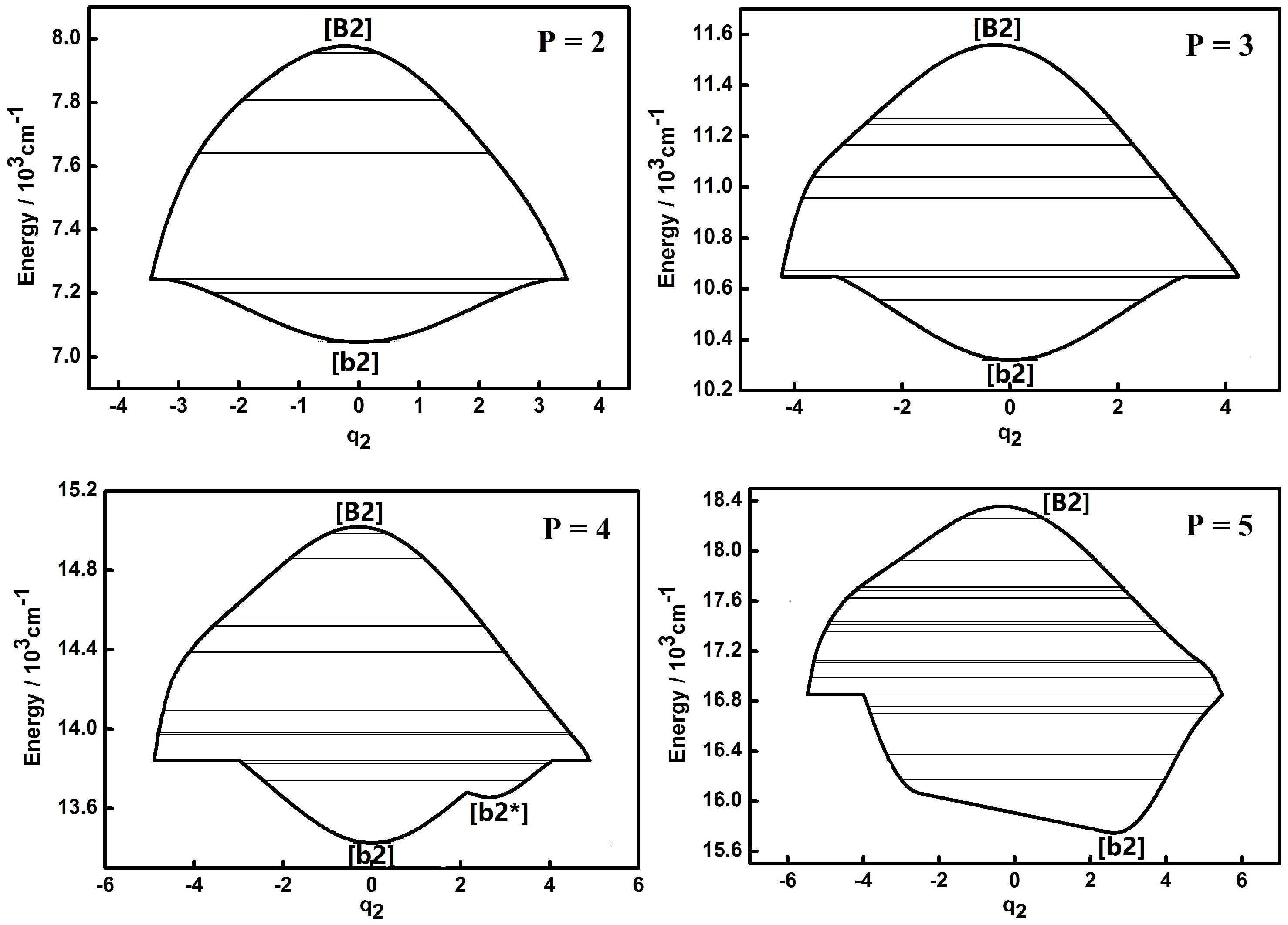
3. Dynamic Features of Highly Excited Vibrational States in HOCl Non-Integrabel System
3.1. Dynamic Potentials and Their Different Coordinates Representation Features for a Typical P Number
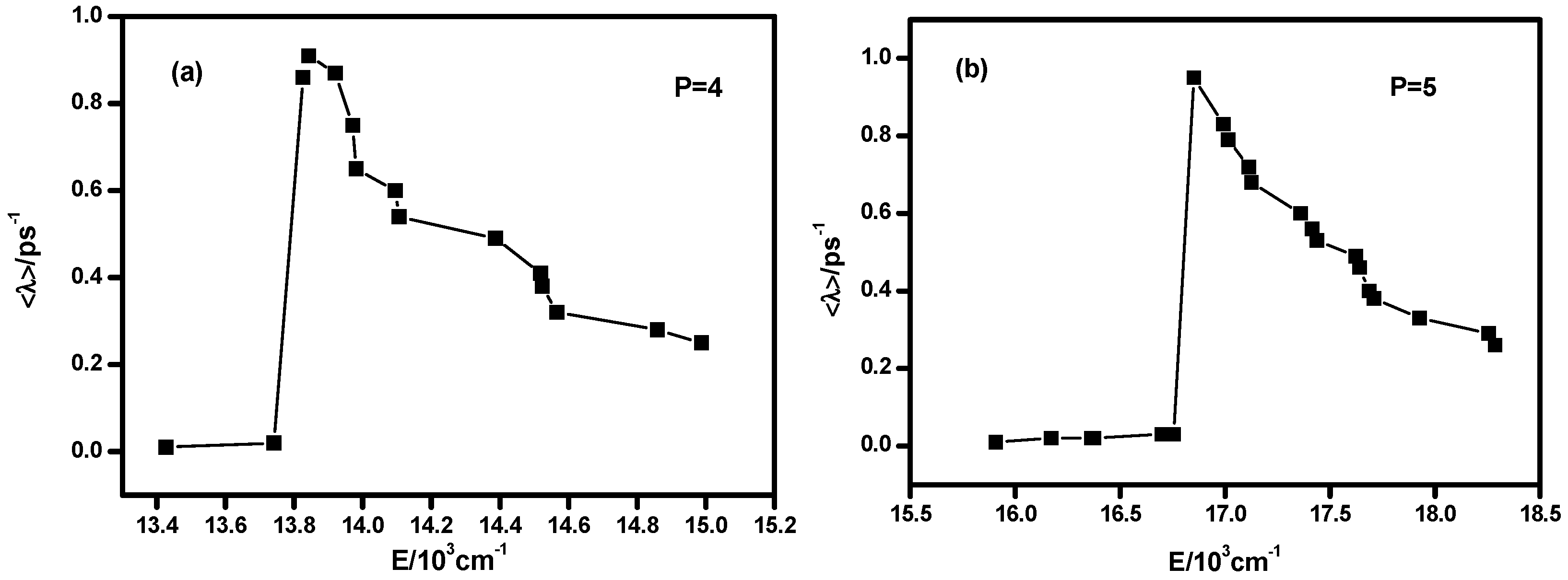
3.2. Lyapunov Exponents and Chaotic Features of Highly Excited Vibrational States under Certain P number
4. Conclusions and Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jost, R.; Joyeux, M.; Skokov, S.; Bowman, J. Vibrational analysis of HOCl up to 98% of the dissociation energy with a Fermi resonance Hamiltonian. J. Chem. Phys. 1999, 111, 6807–6820. [Google Scholar] [CrossRef]
- Peterson, K.A.; Skokov, S.; Bowman, J. A theoretical study of the vibrational energy spectrum of the HOCl/HClO system on an accurate ab initio potential energy surface. J. Chem. Phys. 1999, 111, 7446–7456. [Google Scholar] [CrossRef]
- Joyeux, M.; Farantos, S.C.; Schinke, R. Highly excited motion in molecules: Saddle-node bifurcations and their fingerprints in vibrational spectra. J. Chem. Phys. 2002, 106, 5407–5421. [Google Scholar] [CrossRef]
- Joyeux, M.; Sugny, D.; Lombardi, M.; Jost, R.; Schinke, R.; Skokov, S.; Bowman, J. Vibrational dynamics up to the dissociation threshold: A case study of two-dimensional HOCl. J. Chem. Phys. 2000, 113, 9610–9621. [Google Scholar] [CrossRef] [Green Version]
- Joyeux, M.; Grebenshchikov, S.Y.; Bredenbeck, J.; Schinke, R.; Farantos, S.C. Phase Space Geometry of Multi-dimensional Dynamic Systems and Reaction Processes. In Geometric Structures of Phase Space in Multidimensional Chaos: Applications to Chemical Reaction Dynamics in Complex Systems; John Wiley & Sons: Hoboken, NJ, USA, 2005; Volume 130, pp. 133–139. [Google Scholar]
- Weiss, J.; Hauschildt, J.; Grebenshchikov, S.Y.; Duren, R.; Schinke, R.; Koput, J.; Stamatiadis, S.; Farantos, S.C. Saddle-node bifurcations in the spectrum of HOCl. J. Chem. Phys. 2000, 112, 77–79. [Google Scholar] [CrossRef]
- Fang, C.; Wu, G.Z. Dynamical similarity in the highly excited vibrations of HCP and DCP: The dynamical potential approach. Comput. Theor. Chem. 2009, 910, 141–147. [Google Scholar] [CrossRef]
- Fang, C.; Wu, G.Z. Dynamical potential approach to dissociation of H–C bond in HCO highly excited vibration. Chin. Phys. B 2009, 18, 130–135. [Google Scholar]
- Zhang, C.; Fang, C.; Wu, G.Z. Bending localization of nitrous oxide under anharmonicity and Fermi coupling: The dynamical potential approach. Chin. Phys. B 2010, 19, 110513:1–110513:6. [Google Scholar] [CrossRef]
- Fang, C.; Wu, G.Z. Global dynamical analysis of vibrational manifolds of HOCl and HOBr under anharmonicity and Fermi resonance: The dynamical potential approach. Chin. Phys. B 2010, 19. [Google Scholar] [CrossRef]
- Wang, A.X.; Liu, Y.B.; Fang, C. The study of the dynamic potentials of highly excited vibrational states in HOCl molecular system. Acta Phys. Sin. 2012, 61. [Google Scholar] [CrossRef]
- Wang, A.X.; Sun, L.F.; Fang, C.; Liu, Y.B. The study of dynamic potentials of highly excited vibrational states of HOBr. Int. J. Mol. Sci. 2013, 14, 5250–5263. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.X.; Fang, C.; Liu, Y.B. The Study of Dynamic Potentials of Highly Excited Vibrational States of DCP: From Case Analysis to Comparative Study with HCP. Int. J. Mol. Sci. 2016, 17, 1280. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.M.; Feng, D.H.; Gilmore, R. Coherent states: Theory and some applications. Rev. Mod. Phys. 1990, 62, 867–927. [Google Scholar] [CrossRef]
- Wu, G.Z. Nonlinearity and Chaos in Molecular Vibrations; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Benettin, G.; Galgani, L.; Giorgilli, A.; Strelcyn, J.M. Lyapunov characteristic exponents for smooth dynamical systems and for hamiltonian systems; a method for computing all of them. Part 1: Theory. Meccanica 1980, 15, 9–20. [Google Scholar] [CrossRef]
- Benettin, G.; Galgani, L.; Strelcyn, J.M. Kolmogorov entropy and numerical experiments. Phys. Rev. A 1976, 14, 2338–2345. [Google Scholar] [CrossRef]
- Huang, J.; Wu, G.Z. Dynamical potential approach to DCO highly excited vibration. Chem. Phys. Lett. 2007, 439, 231–235. [Google Scholar] [CrossRef]
- Wu, G.Z. The dynamics of energy transfer of an SU (3) algebraic vibrational system in the coset space representation. Chem. Phys. Lett. 1994, 227, 682–687. [Google Scholar] [CrossRef]
- Sample Availability: Not available.



| Parameter | Values (cm−1) | Parameter | Values (cm−1) |
|---|---|---|---|
| ω1 | 3777.067 | z2222 | −0.04117 |
| ω2 | 1258.914 | z3333 | −0.00171 |
| ω3 | 753.834 | z1122 | −0.15070 |
| X11 | −80.277 | z1222 | 0.13189 |
| X12 | −19.985 | z2333 | −0.01229 |
| X22 | −3.204 | z1233 | 0.02381 |
| X23 | −10.637 | z22222 | 0.00151 |
| X33 | −7.123 | z22333 | −0.00066 |
| y111 | −0.3619 | k | 0 |
| y333 | 0.0825 | k2 | −0.76017 |
| y122 | −1.9534 | k3 | −0.24939 |
| y133 | −0.0532 | k22 | −0.01158 |
| y223 | −0.0802 | k23 | 0.04075 |
| y233 | −0.2503 | k33 | 0.00583 |
| KKK | 0.19520 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, A.; Fang, C.; Liu, Y. Dynamic Features of the Highly Excited Vibrational States of the HOCl Non-Integrable System Based on the Dynamic Potential and Lyapunov Exponent Approaches. Molecules 2017, 22, 101. https://doi.org/10.3390/molecules22010101
Wang A, Fang C, Liu Y. Dynamic Features of the Highly Excited Vibrational States of the HOCl Non-Integrable System Based on the Dynamic Potential and Lyapunov Exponent Approaches. Molecules. 2017; 22(1):101. https://doi.org/10.3390/molecules22010101
Chicago/Turabian StyleWang, Aixing, Chao Fang, and Yibao Liu. 2017. "Dynamic Features of the Highly Excited Vibrational States of the HOCl Non-Integrable System Based on the Dynamic Potential and Lyapunov Exponent Approaches" Molecules 22, no. 1: 101. https://doi.org/10.3390/molecules22010101






