Microscale Diffusion Measurements and Simulation of a Scaffold with a Permeable Strut
Abstract
:1. Introduction
2. Results and Discussion
2.1. Fabrication of the Electrospun Nanofibrous Patterns
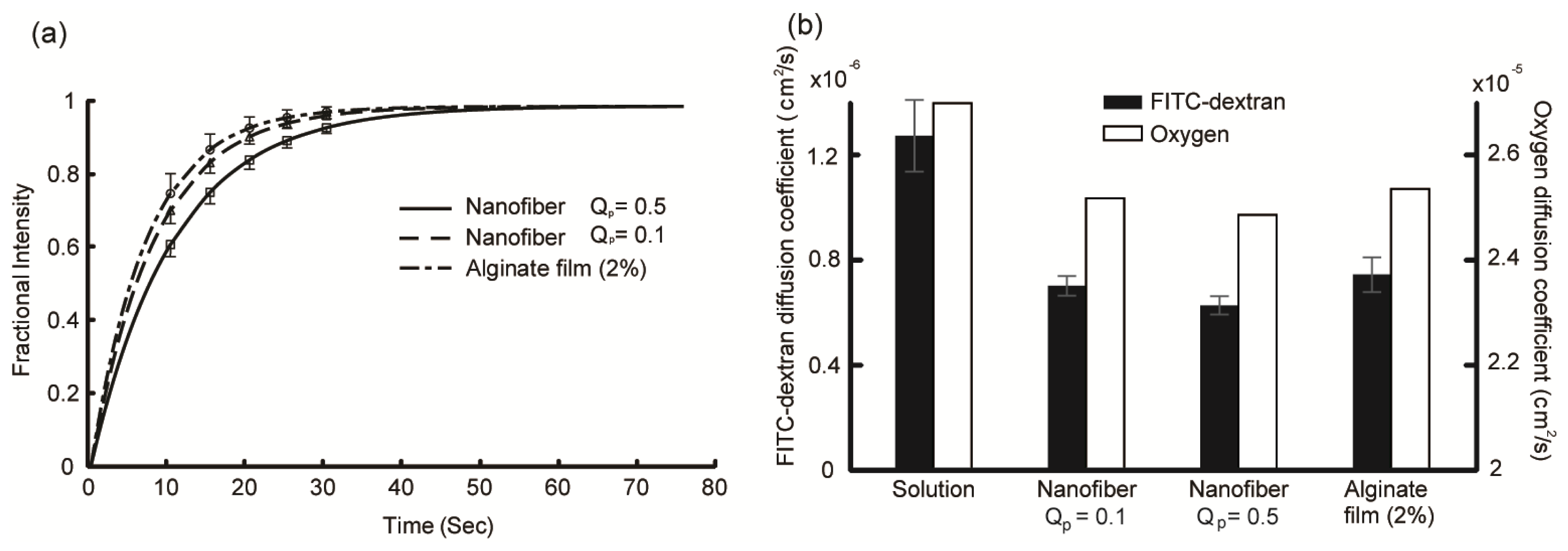
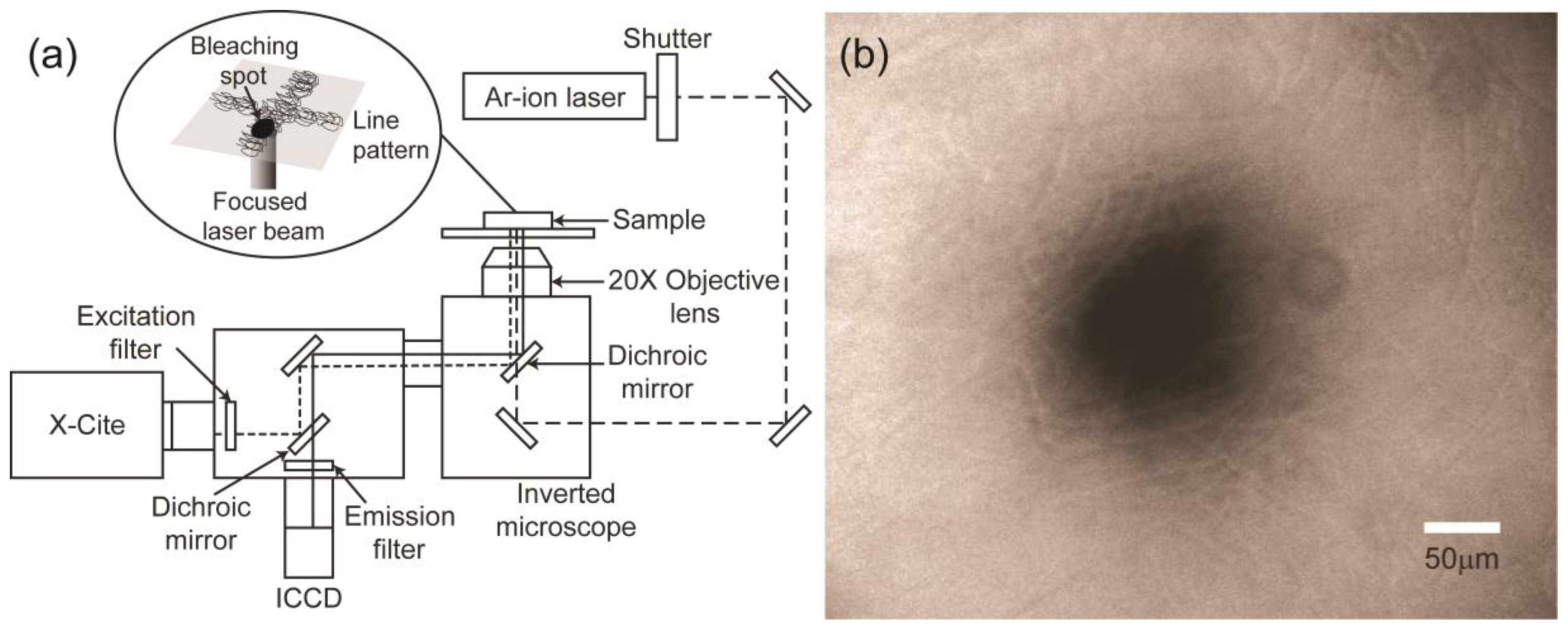
2.2. Diffusion Coefficient Measurements Using FRAP
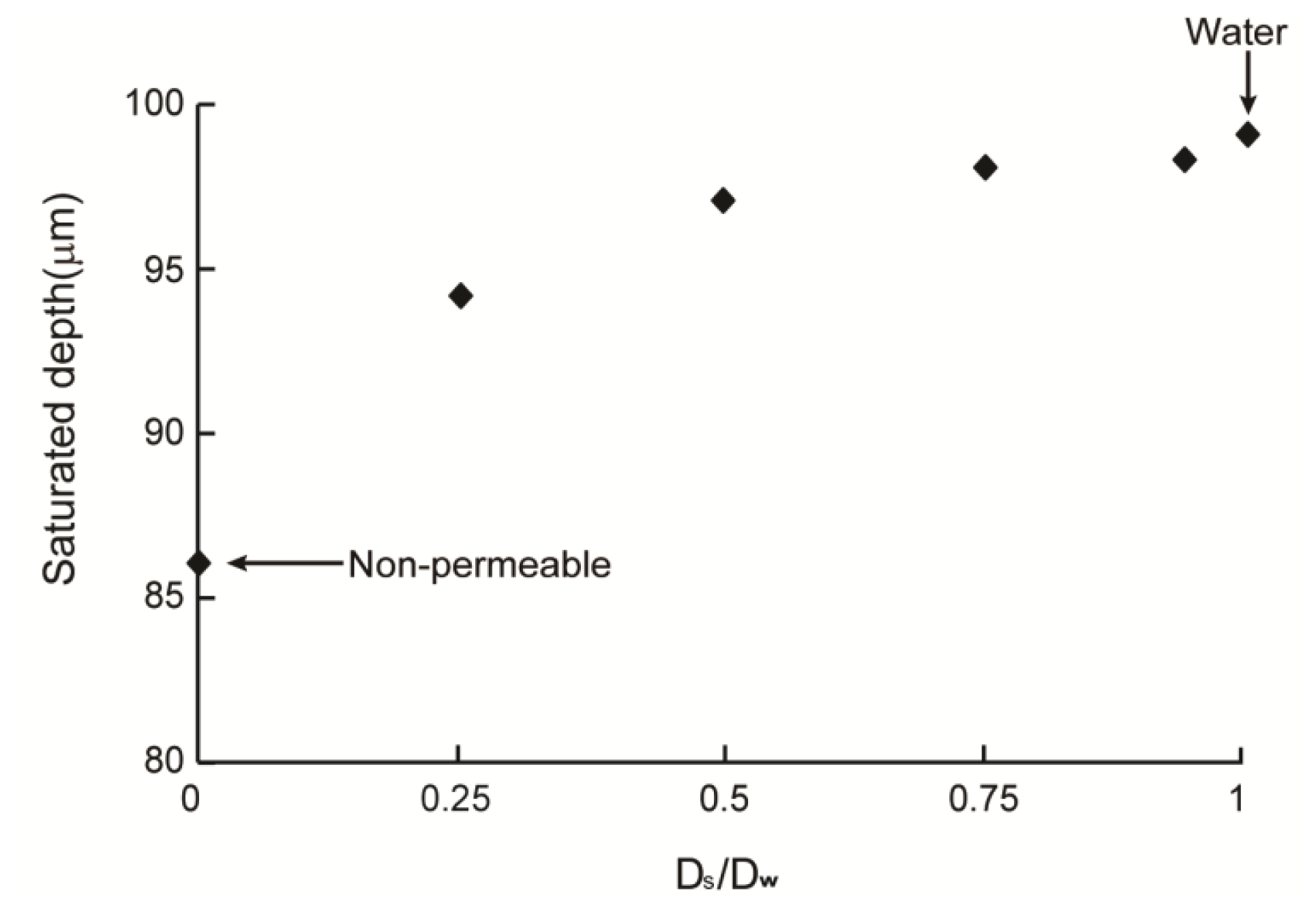
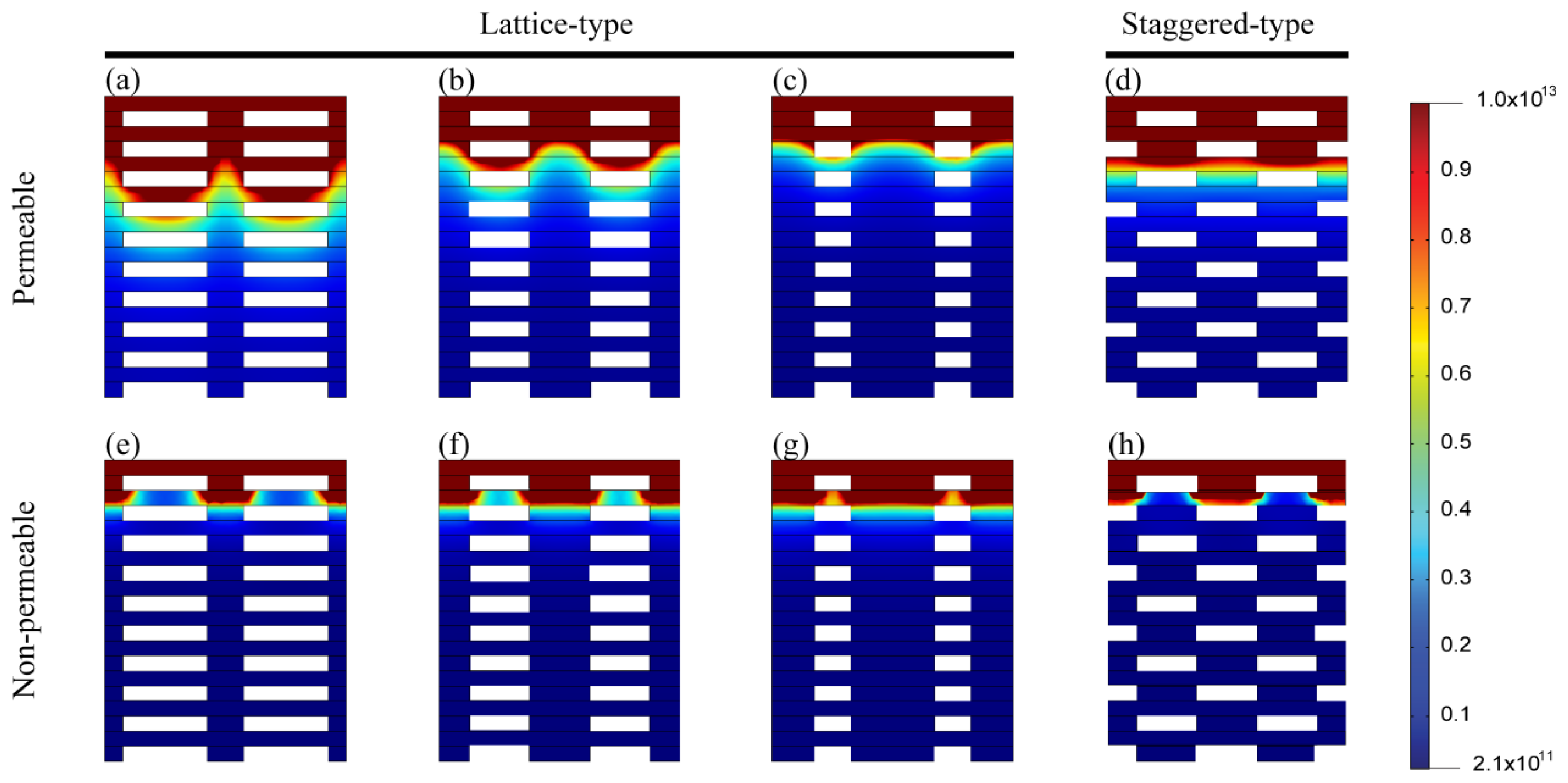
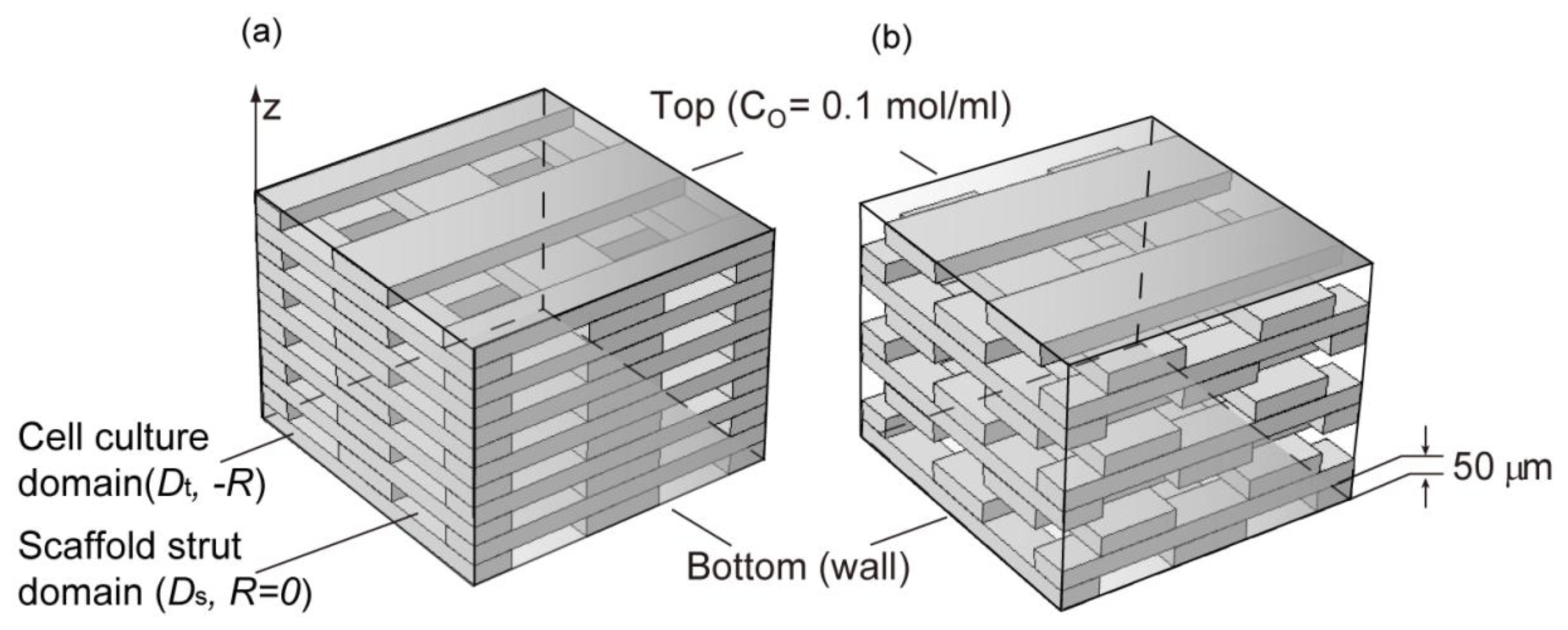
2.3. Cell Density Distribution Simulated within the Spatially Patterned Scaffold
3. Materials and Methods
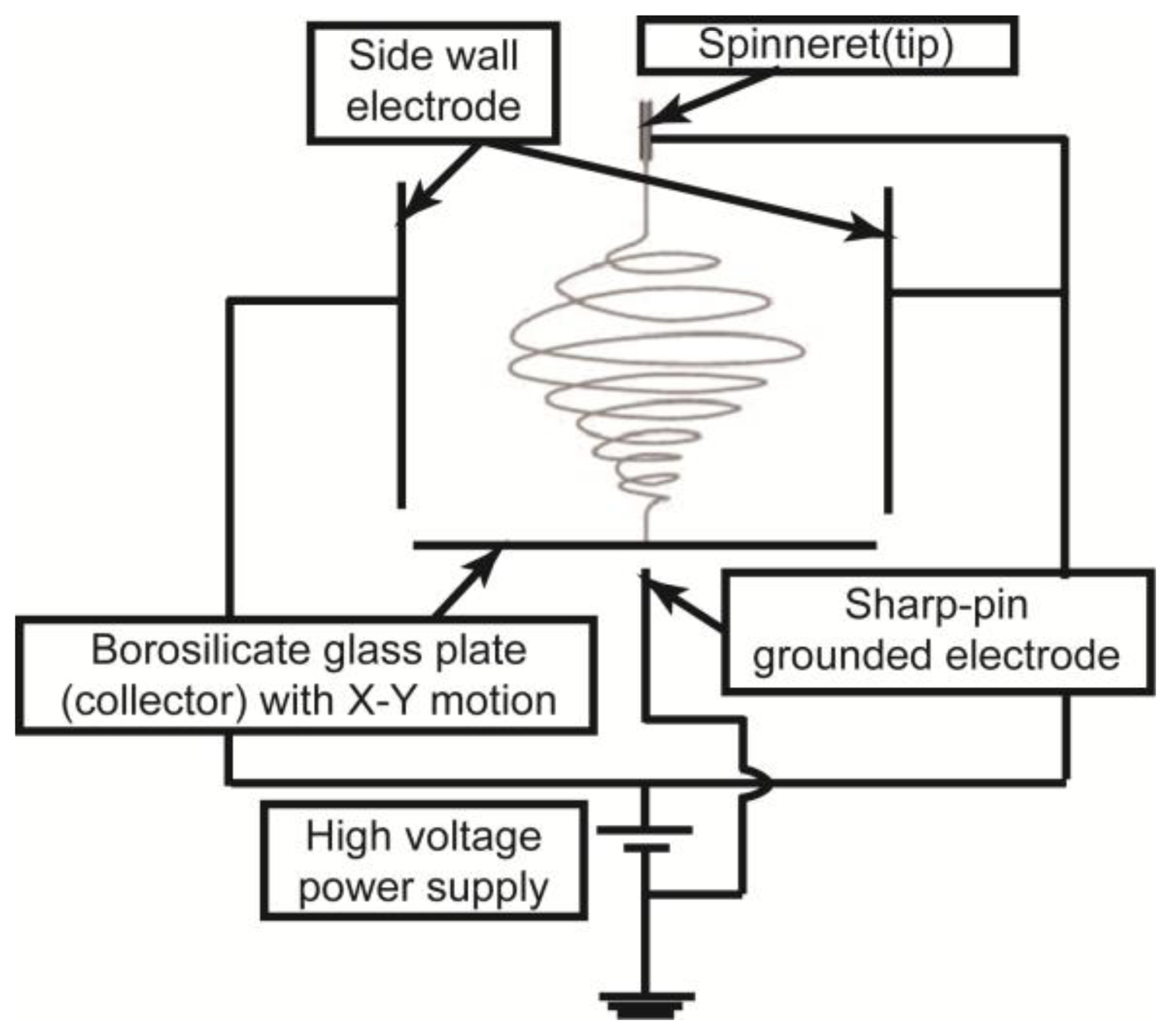
3.1. DWES Apparatus
3.2. Sample Preparation
3.3. FRAP Method
3.4. Simulation of Cell Density Distribution in a Scaffold
4. Conclusions


| Parameter | Definition | Value | Ref. |
|---|---|---|---|
| Vmax | Maximum cellular oxygen consumption rate | 3.3 × 10−16 mol/cell/s | [46] |
| Km | Half-maximum rate oxygen concentration | 3.79 × 10−3 mol/m3 | [47] |
| K | Saturation constant in Monod kinetics | 3 nmol/mL | [46] |
| C0 | Maximum dissolved oxygen concentration | 0.1 mol/m3 | [28] |
| Dt | Oxygen diffusion coefficient in typical tissue culture sysyem | 2.0 × 10−5 cm2/s | [28] |
| Ds | Oxygen diffusion coefficient in scaffold strut domain | 0–2.68 × 10−5 cm2/s | - |
| td | minimum cell division time | 36.5 h | [45] |
Acknowledgments
Conflicts of Interest
References
- Tejas, K.; Agrawal, C.; Joo, O. Diffusion in musculoskeletal tissue engineering scaffolds: Design issues related to porosity, permeability, architecture, and nutrient mixing. Ann. Biomed. Eng 2004, 32, 1728–1743. [Google Scholar]
- Yang, J.; Shi, G.; Bei, J.; Wang, S.; Cao, Y.; Shang, Q.; Yang, G.; Wang, W. Fabrication and surface modification of macroporous poly(l-lactic acid) and poly(l-lactic-co-glycolic acid) (70/30) cell scaffolds for human skin fibroblast cell culture. J. Biomed. Mater. Res. A 2002, 62, 438–446. [Google Scholar]
- Ho, M.H.; Kuo, P.Y.; Hsieh, H.J.; Hsien, T.Y.; Hou, L.T.; Lai, J.Y.; Wang, D.M. Preparation of porous scaffolds by using freeze-extraction and freeze-gelation methods. Biomaterials 2004, 25, 129–138. [Google Scholar]
- Whang, K.; Thomas, C.H.; Healy, K.E.; Nuber, G. A novel method to fabricate bioabsorbable scaffolds. Polymer 1995, 36, 837–842. [Google Scholar]
- Wang, X.; Li, W.; Kumar, V. A method for solvent-free fabrication of porous polymer using solid-state foaming and ultrasound for tissue engineering applications. Biomaterials 2006, 27, 1924–1929. [Google Scholar]
- Singh, L.; Kumar, V.; Ratner, B.D. Generation of porous microcellular 85/15 poly (dl-lactide-co-glycolide) foams for biomedical applications. Biomaterials 2004, 25, 2611–2617. [Google Scholar]
- Hou, Q.; Grijpma, D.W.; Feijen, J. Porous polymeric structures for tissue engineering prepared by a coagulation, compression moulding and salt leaching technique. Biomaterials 2003, 24, 1937–1947. [Google Scholar]
- Zein, I.; Hutmacher, D.W.; Tan, K.C.; Teoh, S.H. Fused deposition modeling of novel scaffold architectures for tissue engineering applications. Biomaterials 2002, 23, 1169–1185. [Google Scholar]
- Yeong, W.Y.; Chua, C.K.; Leong, K.F.; Chandrasekaran, M. Rapid prototyping in tissue engineering: Challenges and potential. Trends Biotechnol 2004, 22, 643–652. [Google Scholar]
- Bartolo, P.J.; Chua, C.K.; Almeida, H.A.; Chou, S.M.; Lim, A.S.C. Biomanufacturing for tissue engineering: Present and future trends. Virtual Phys. Prototyp 2012, 7, 13–24. [Google Scholar]
- Yang, S.; Leong, K.F.; Du, Z.; Chua, C.K. The design of scaffolds for use in tissue engineering. Part II. Rapid prototyping techniques. Tissue Eng 2002, 8, 1–11. [Google Scholar]
- Li, W.J.; Laurencin, C.T.; Caterson, E.J.; Tuan, R.S.; Ko, F.K. Electrospun nanofibrous structure: A novel scaffold for tissue engineering. J. Biomed. Mater. Res 2002, 60, 613–621. [Google Scholar]
- Miao, J.; Miyauchi, M.; Simmons, T.J.; Dordick, J.S.; Linhardt, R.J. Electrospinning of nanomaterials and applications in electronic components and devices. J. Nanosci. Nanotechnol 2010, 10, 5507–5519. [Google Scholar]
- Xin, X.; Hussain, M.; Mao, J.J. Continuing differentiation of human mesenchymal stem cells and induced chondrogenic and osteogenic lineages in electrospun PLGA nanofiber scaffold. Biomaterials 2007, 28, 316–325. [Google Scholar]
- Baker, S.C.; Atkin, N.; Gunning, P.A.; Granville, N.; Wilson, K.; Wilson, D.; Southgate, J. Characterisation of electrospun polystyrene scaffolds for three-dimensional in vitro biological studies. Biomaterials 2006, 27, 3136–3146. [Google Scholar]
- Yang, S.; Leong, K.F.; Du, Z.; Chua, C.K. The design of scaffolds for use in tissue engineering. Part I. Traditional Factors. Tissue Eng 2001, 7, 679–689. [Google Scholar]
- Depan, D.; Girase, B.; Shah, J.S.; Misra, R.D. Structure-process-property relationship of the polar graphene oxide-mediated cellular response and stimulated growth of osteoblasts on hybrid chitosan network structure nanocomposite scaffolds. Acta Biomater 2011, 7, 3432–3445. [Google Scholar]
- Depan, D.; Surya, P.K.; Girase, B.; Misra, R.D. Organic/inorganic hybrid network structure nanocomposite scaffolds based on grafted chitosan for tissue engineering. Acta Biomater 2011, 7, 2163–2175. [Google Scholar]
- Yuan, Q.; Hein, S.; Misra, R.D. New generation of chitosan-encapsulated ZnO quantum dots loaded with drug: Synthesis, characterization and in vitro drug delivery response. Acta Biomater 2010, 6, 2732–2739. [Google Scholar]
- Yuan, Q.; Shah, J.; Hein, S.; Misra, R.D. Controlled and extended drug release behavior of chitosan-based nanoparticle carrier. Acta Biomater 2010, 6, 61140–61148. [Google Scholar]
- Thein-Han, W.W.; Misra, R.D. Biomimetic chitosan-nanohydroxyapatite composite scaffolds for bone tissue engineering. Acta Biomater 2009, 5, 1182–1197. [Google Scholar]
- Thein-Han, W.W.; Saikhun, J.; Pholpramoo, C.; Misra, R.D.; Kitiyanant, Y. Chitosan-gelatin scaffolds for tissue engineering: Physico-chemical properties and biological response of buffalo embryonic stem cells and transfectant of GFP-buffalo embryonic stem cells. Acta Biomater 2009, 5, 3453–3466. [Google Scholar]
- Yuan, Q.; Venkatasubramanian, R.; Hein, S.; Misra, R.D. A stimulus-responsive magnetic nanoparticle drug carrier: Magnetite encapsulated by chitosan-grafted-copolymer. Acta Biomater 2008, 4, 1024–1037. [Google Scholar]
- Zhang, X.; Baughman, C.B.; Kaplan, D.L. In vitro evaluation of electrospun silk fibroin scaffolds for vascular cell growth. Biomaterials 2008, 29, 2217–2227. [Google Scholar]
- Meinel, A.J.; Kubow, K.E.; Klotzsch, E.; Garcia-Fuentes, M.; Smith, M.L.; Vogel, V.; Merkle, H.P.; Meinel, L. Optimization strategies for electrospun silk fibroin tissue engineering scaffolds. Biomaterials 2009, 30, 3058–3067. [Google Scholar]
- Bulysheva, A.A.; Bowlin, G.L.; Klingelhutz, A.J.; Yeudall, W.A. Low-temperature electrospun silk scaffold for in vitro mucosal modeling. J. Biomed. Mater. Res. A 2012, 100, 757–767. [Google Scholar]
- Lee, J.; Lee, S.Y.; Jang, J.; Jeong, Y.H.; Cho, D.W. Fabrication of patterned nanofibrous mats using direct-write electrospinning. Langmuir 2012, 28, 7267–7275. [Google Scholar]
- Dunn, J.C.; Chan, W.Y.; Cristini, V.; Kim, J.S.; Lowengrub, J.; Singh, S.; Wu, B.M. Analysis of cell growth in three-dimensional scaffolds. Tissue Eng 2006, 12, 705–716. [Google Scholar]
- Johnson, E.M.; Berk, D.A.; Jain, R.K.; Deen, W.M. Diffusion and partitioning of proteins in charged agarose gels. Biophys. J 1995, 68, 1561–1568. [Google Scholar]
- Androjna, C.; Gatica, J.E.; Belovich, J.M.; Derwin, K.A. Oxygen diffusion through natural extracellular matrices: Implications for estimating “critical thickness” values in tendon tissue engineering. Tissue Eng. Part A 2008, 14, 559–569. [Google Scholar]
- Soumpasis, D.M. Theoretical analysis of fluorescence photobleaching recovery experiments. Biophys. J 1983, 41, 95–97. [Google Scholar]
- Lawrence, J.R.; Wolfaardt, G.M.; Korber, D.R. Determination of diffusion coefficients in biofilms by confocal laser microscopy. Appl. Environ. Microbiol 1994, 60, 1166–1173. [Google Scholar]
- Arrio-Dupont, M.; Cribier, S.; Foucault, G.; Devaux, P.F.; D’Albis, A. Diffusion of fluorescently labeled macromolecules in cultured muscle cells. Biophys. J 1996, 70, 2327–2332. [Google Scholar]
- Ogston, A.G.; Preston, B.N.; Wells, J.D. On the transport of compact particles through solutions of chain-polymers. Proc. R. Soc. A 1973, 333, 297–316. [Google Scholar]
- Burns-Bellhorn, M.S.; Bellhorn, R.W.; Benjamin, J.V. Anterior segment permeability to fluorescein-labeled dextrans in the rat. Invest. Ophthalmol. Vis. Sci 1978, 17, 857–862. [Google Scholar]
- Reginald, H.G.; Charles, M.G. Biochemistry, 3rd ed; Thomson learning: Belmont, CA, USA, 2007; pp. 31–32. [Google Scholar]
- Stewart, P.S. Diffusion in biofilms. J. Bacteriol 2003, 185, 1485–1491. [Google Scholar]
- Bosma, J.C.; Wesselingh, J.A. Partitioning and diffusion of large molecules in fibrous structures. J. Chromatogr 2000, 743, 169–180. [Google Scholar]
- Mehmetoglu, U.; Ates, S.; Berber, R. Oxygen diffusivity in calcium alginate gel beads containing gluconobacter suboxydans. Artif. Cells Blood Substit. Immobil. Biotechnol 1996, 24, 91–106. [Google Scholar]
- Hulst, A.C.; Hens, H.J.H.; Buitelaar, R.M.; Tramper, J. Determination of the effective diffusion coefficient of oxygen in gel materials in relation to gel concentration. Biotechnol. Tech 1989, 3, 199–204. [Google Scholar]
- Lee, J.; Jang, J.; Oh, H.; Jeong, Y.H.; Cho, D.W. Fabrication of a three-dimensional nanofibrous scaffold with lattice pores using direct-write electrospinning. Mater. Lett 2013, 93, 397–400. [Google Scholar]
- Cheng, G.; Markenscoff, P.; Zygourakis, K. A 3D hybrid model for tissue growth: The interplay between cell population and mass transport dynamics. Biophys. J 2009, 97, 401–414. [Google Scholar]
- Heinemann, A.; Wischhusen, F.; Puschel, K.; Rogiers, X. Standard liver volume in the Caucasian populssation. Liver Transpl. Surg 1999, 5, 366–368. [Google Scholar]
- Li, A.P. Human hepatocytes: Isolation, cryopreservation and applications in drug development. Chem. Biol. Interact 2007, 168, 16–29. [Google Scholar]
- Kino-Oka, M.; Maeda, Y.; Yamamoto, T.; Sugawara, K.; Taya, M. A kinetic modeling of chondrocyte culture for manufacture of tissue-engineered cartilage. J. Biosci. Bioeng 2005, 99, 197–207. [Google Scholar]
- Croll, T.I.; Gentz, S.; Mueller, K.; Davidson, M.; O’Connor, A.J.; Stevens, G.W.; Cooper-White, J.J. Modelling oxygen diffusion and cell growth in a porous, vascularizing scaffold for soft tissue engineering applications. Chem. Eng. Sci 2005, 60, 4924–4934. [Google Scholar]
- Brown, D.A.; MacLellan, W.R.; Laks, H.; Dunn, J.C.; Wu, B.M.; Beygui, R.E. Analysis of oxygen transport in a diffusion-limited model of engineered heart tissue. Biotechnol. Bioeng 2007, 97, 962–975. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lee, S.Y.; Lee, B.R.; Lee, J.; Kim, S.; Kim, J.K.; Jeong, Y.H.; Jin, S. Microscale Diffusion Measurements and Simulation of a Scaffold with a Permeable Strut. Int. J. Mol. Sci. 2013, 14, 20157-20170. https://doi.org/10.3390/ijms141020157
Lee SY, Lee BR, Lee J, Kim S, Kim JK, Jeong YH, Jin S. Microscale Diffusion Measurements and Simulation of a Scaffold with a Permeable Strut. International Journal of Molecular Sciences. 2013; 14(10):20157-20170. https://doi.org/10.3390/ijms141020157
Chicago/Turabian StyleLee, Seung Youl, Byung Ryong Lee, Jongwan Lee, Seongjun Kim, Jung Kyung Kim, Young Hun Jeong, and Songwan Jin. 2013. "Microscale Diffusion Measurements and Simulation of a Scaffold with a Permeable Strut" International Journal of Molecular Sciences 14, no. 10: 20157-20170. https://doi.org/10.3390/ijms141020157





