Structural transitions in biomolecules - a numerical comparison of two approaches for the study of phase transitions in small systems
Abstract
:1 Introduction
2 Analysis of Partition Function Zeros in Small Systems
| N | Re(u1) | Im(u1) | Re(u2) | Im(u2) |
| 10 | 0.30530(12) | 0.07720(14) | 0.2823(13) | 0.13820(61) |
| 15 | 0.356863(61) | 0.053346(39) | 0.34167(60) | 0.10440(59) |
| 20 | 0.374016(41) | 0.042331(45) | 0.36161(27) | 0.08109(24) |
| 30 | 0.378189(19) | 0.027167(32) | 0.37399(14) | 0.05420(27) |
| N | Re(u3) | Im(u3) | Re(u4) | Im(u4) |
| 10 | 0.2459(72) | 0.1851(63) | 0.172(11) | 0.2200(71) |
| 15 | 0.3331(48) | 0.1454(28) | 0.3067(81) | 0.1689(32) |
| 20 | 0.3569(27) | 0.1154(13) | 0.3336(56) | 0.1470(27) |
| 30 | 0.3693(11) | 0.0804(13) | 0.35854(63) | 0.1022(43) |
| N | αu | γu |
| 10 | -0.36(17) | -0.365(17) |
| 15 | 0.41(19) | -0.291(11) |
| 20 | 0.06(14) | -0.3229(78) |
| 30 | 0.19(14) | -0.1568(58) |
| N | a1 | a2 | a3 |
| 10 | 6.17(60) | 1.862(46) | 0.01(14) |
| 15 | 4.37(19) | 1.664(16) | 0.014(69) |
| 20 | 3.62(26) | 1.558(24) | -0.014(98) |
| 30 | 3.54(31) | 1.473(30) | -0.007(61) |
| Re(u1) | Im(u1) | Re(u2) | Im(u2) | Re(u3) | Im(u3) | Re(u4) | Im(u4) |
| 0.349620 | 0.047937 | 0.361590 | 0.072467 | 0.320531 | 0.097282 | 0.370090 | 0.132103 |
| 0.144820 | 0.039763 | 0.104362 | 0.077531 | 0.074312 | 0.100345 | 0.033091 | 0.116098 |
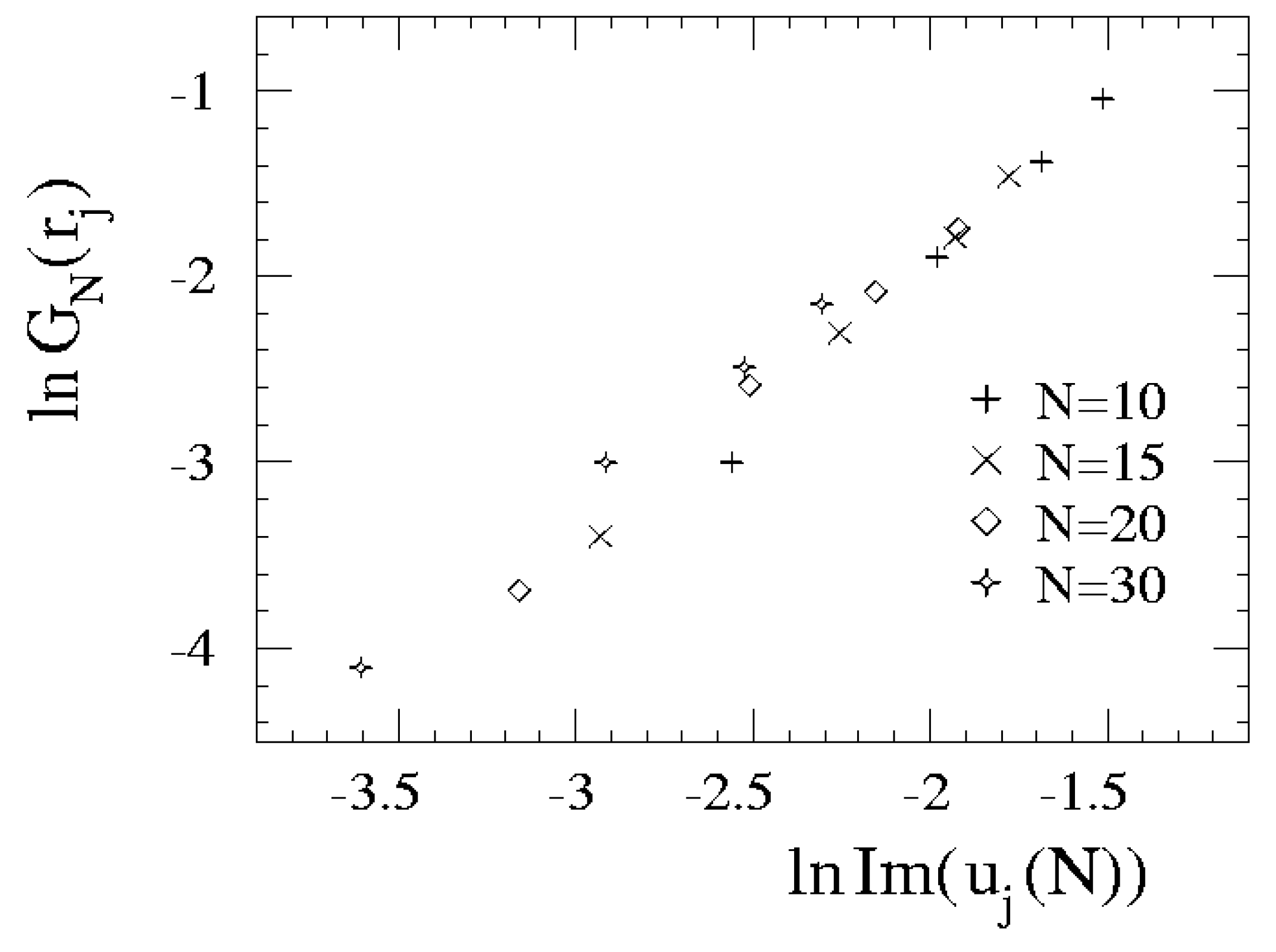
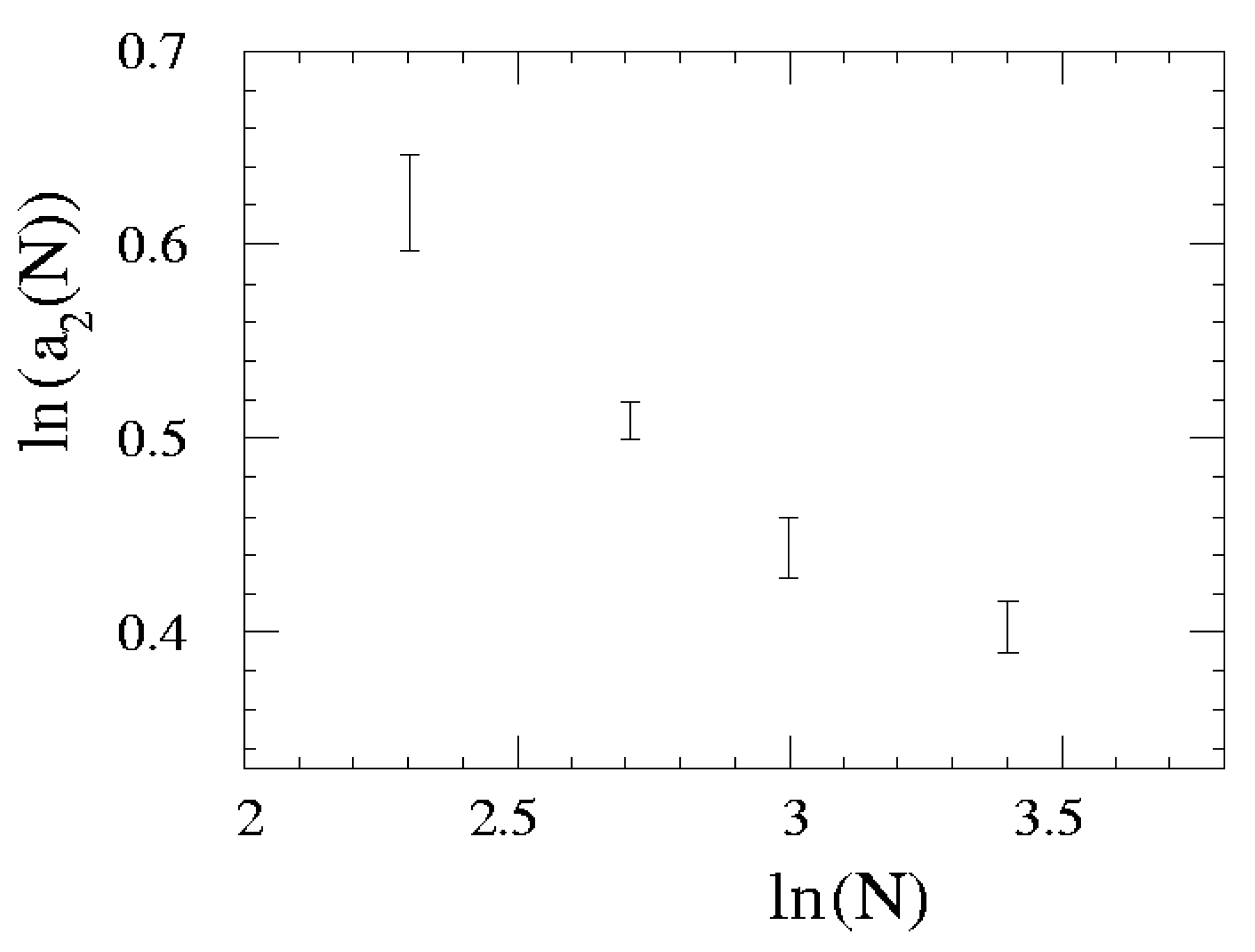
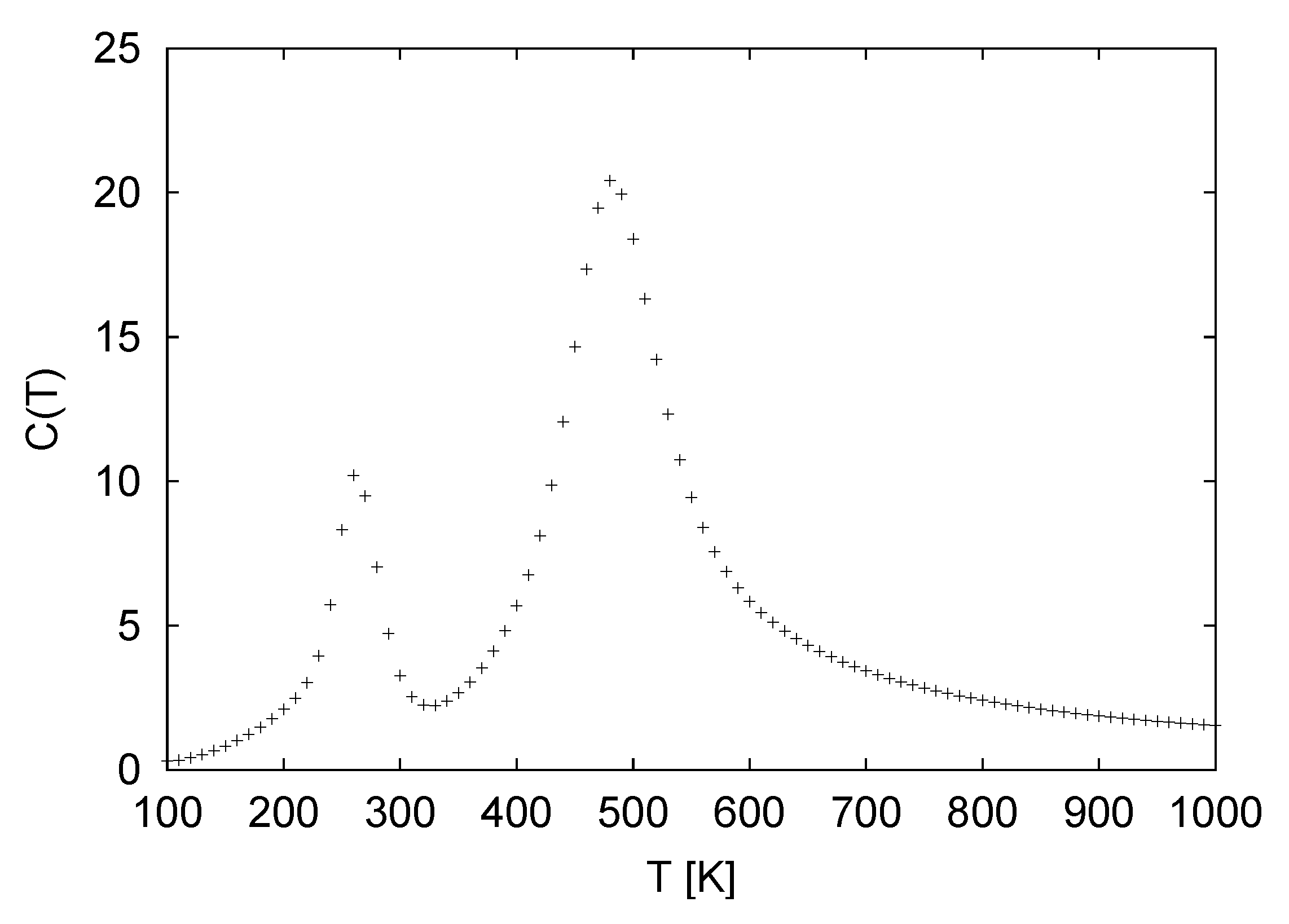
Conclusion
Acknowledgements
References
- Berry, R.S.; Smirnov, B.M. Phase Stability of Solid Clusters. J. Chem. Phys. 2000, 113, 728–737. [Google Scholar] [CrossRef] Berry, R.S.; Smirnov, B.M. Structural Phase Transition in a Large Cluster. J. Exp. Theor. Phys. 2000, 90, 491–498. [Google Scholar] [CrossRef] Proykova, A.; Radev, R.; Li, F.-Y.; Berry, R.S. Structural Transitions in Small Molecular Clusters. J. Chem. Phys. 1999, 110, 3887–3896. [Google Scholar] [CrossRef] Nayak, S.K.; Jena, P.; Ball, K.D.; Berry, R.S. Dynamics and Instabilities Near the Glass Transition: From Clusters to Crystals. J. Chem. Phys. 1998, 108, 234–239. [Google Scholar] [CrossRef] Proykova, A.; Berry, R.S. Analogues in Clusters of SecondOrder Transitions ? Z. Phys. D. 1997, 40, 215–220. [Google Scholar] [CrossRef] Wales, D.J.; Berry, R.S. Coexistence in Finite Systems. Phys. Rev. Lett. 1994, 73, 2875–2878. [Google Scholar] [CrossRef] [PubMed]Kunz, R.E.; Berry, R.S. Coexistence of Multiple Phases in Finite Systems. Phys. Rev. Lett. 1993, 71, 3987–3990. [Google Scholar] [CrossRef] [PubMed]
- Borrmann, P.; Mülken, O.; Harting, J. Classification of Phase Transitions in Small Systems. Phys. Rev. Lett. 2000, 84, 3511–3514. [Google Scholar] [CrossRef] [PubMed]Mülken, O.; Borrmann, P.; Harting, J.; Stamerjohanns, H. Classification of Phase Transitions of Finite Bose-Einstein Condensates in Power-Law Traps by Fisher Zeros. Phys. Rev. A. 2001, 64, 013611-1–013611-6. [Google Scholar] Mülken, O.; Borrmann, P. Classification of the Nuclear Multifragmentation Phase Transition. Phys. Rev. C. 2001, 63, 024306-1–024306-4. [Google Scholar]
- Grossmann, S.; Rosenhauer, W. Temperature Dependence Near Phase Transitions in Classical and Quant. Mech. Canonical Statistics. Z. Physik. 1967, 207, 138–152. [Google Scholar]
- Grossmann, S.; Rosenhauer, W. Phase Transitions and the Distribution of Temperature Zeros of the Partition Function. Z. Physik. 1969, 218, 437–448. [Google Scholar] [CrossRef] Grossmann, S.; Rosenhauer, W. Phase Transitions and the Distribution of Temperature Zeros of the Partition Function. Z. Physik. 1969, 218, 449–459. [Google Scholar] [CrossRef]
- Janke, W.; Kenna, R. The Strength of First and Second Order Phase Transitions from Partition Function Zeroes. J. Stat. Phys. 2001, 102, 1211–1227. [Google Scholar] [CrossRef]
- Yang, C.N.; Lee, T.D. Statistical Theory of Equations of State and Phase Transitions. I. Theory of Condensation. Phys. Rev. 1952, 87, 404–409. [Google Scholar] Lee, T.D.; Yang, C.N. Statistical Theory of Equations of State and Phase Transitions. II. Lattice Gas and Ising Model. Phys. Rev. 1952, 87, 410–419. [Google Scholar]
- Fisher, M.E. Lectures in Theoretical Physics. University of Colorado Press: Boulder, 1965; Vol. 7c, p. 1. [Google Scholar]
- Villanova, R. Ph.D. Thesis, Florida State University, 1991.
- Villanova, R.; Alves, N.A.; Berg, B.A. Density of States and Finite Size Scaling Investigations. Nucl. Phys. B (Proc. Suppl.) 1991, 20, 665–668. [Google Scholar] [CrossRef]
- Alves, N.A.; Berg, B.A.; Villanova, R. Potts Models: Density of States and Mass Gap from Monte Carlo Calculations. Phys. Rev. B 1991, 43, 5846–5856. [Google Scholar] [CrossRef]
- Alves, N.A.; Ferrite, J.P.N.; Hansmann, U.H.E. Numerical Comparison of Two Approaches for the Study of Phase Transitions in Small Systems. Phys. Rev. E 2002, 65, 036110–036110-9. [Google Scholar] [CrossRef] [PubMed]
- Poland, D.; Scheraga, H.A. Theory of Helix-Coil Transitions in Biopolymers. Academic Press: New York, 1970. [Google Scholar]
- Hansmann, U.H.E.; Okamoto, Y. Finite-Size Scaling of Helix-Coil Transitions in Poly-alanine Studied by Multicanonical Simulations. J. Chem. Phys. 1999, 110, 1267–1276, 111, 1339(E). [Google Scholar] [CrossRef]
- Alves, N.A.; Hansmann, U.H.E. Partition Function Zeros and Finite Size Scaling of Helix-Coil Transitions in a Polypeptide. Phys. Rev. Lett. 2000, 84, 1836–1839. [Google Scholar] [CrossRef] [PubMed]
- Kemp, J.P.; Hansmann, U.H.E.; Chen, Zh.Y. Is There a Universality of the Helix-Coil Transition in Protein Models ? Eur. Phy. J. B 2000, 15, 371–374. [Google Scholar] [CrossRef]
- Sippl, M.J.; Némethy, G.; Scheraga, H.A. Intermolecular Potentials from Crystal Data. 6. Determination of Empirical Potentials for O-H···O=C Hydrogen Bonds from Packing Configuration. J. Phys. Chem. 1984, 88, 6231–6233, and references therein. [Google Scholar] [CrossRef]
- Berg, B.A.; Neuhaus, T. Multicanonical Algorithms for First Order Phase Transitions. Phys. Lett. B. 1991, 267, 249–253. [Google Scholar] [CrossRef]
- Alves, N.A.; de Felicio, J.R.D.; Hansmann, U.H.E. A New Look at the 2d Ising Model from Exact Partition Function Zeros for Large Lattice Sizes. Int. J. Mod. Phys. C. 1997, 8, 1063–1072. [Google Scholar] [CrossRef] [Green Version]
- Alves, N.A.; Berg, B.A.; Sanielevici, S. Spectral Density Study of the SU(3) Deconfining Phase Transition. Nucl. Phys. B 1992, 376, 218–252. [Google Scholar] [CrossRef]
- Efron, B. Computers and the Theory of Statistics: Thinking the Unthinkable. SIAM Rev. 1979, 21, 460–480. [Google Scholar] [CrossRef] Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap. Monographs on Statistics and Applied Probability. Chapman & Hall, 1993; Vol. 57. [Google Scholar]
- Alves, N.A.; Hansmann, U.H.E. Helix Formation and Folding in an Artifical Peptide. Submitted for publication.
- Eisenmenger, F.; Hansmann, U.H.E.; Hayryan, Sh.; Hu, C.K. [SMMP] A Modern Package for Simulation of Proteins. Comp. Phys. Comm. 2001, 138, 192–212. [Google Scholar] [CrossRef]
© 2002 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Alves, N.A.; Hansmann, U.H.E.; Peng, Y. Structural transitions in biomolecules - a numerical comparison of two approaches for the study of phase transitions in small systems. Int. J. Mol. Sci. 2002, 3, 17-29. https://doi.org/10.3390/i3010017
Alves NA, Hansmann UHE, Peng Y. Structural transitions in biomolecules - a numerical comparison of two approaches for the study of phase transitions in small systems. International Journal of Molecular Sciences. 2002; 3(1):17-29. https://doi.org/10.3390/i3010017
Chicago/Turabian StyleAlves, Nelson A., Ulrich H.E. Hansmann, and Yong Peng. 2002. "Structural transitions in biomolecules - a numerical comparison of two approaches for the study of phase transitions in small systems" International Journal of Molecular Sciences 3, no. 1: 17-29. https://doi.org/10.3390/i3010017



