1 Introduction
Determination of the lowest energy configuration for a cluster of
N atoms is a nontrivial task [
1,
2,
3,
4,
5]. The complexity arises in part from the exponentially (in
N) large number of minima in the potential energy surface [
6]. Furthermore, the geometry of the potential energy landscape itself can make it computationally hard.
The problem is, however, simple to describe: Find the lowest energy minimum of a
N body potential energy surface,
,
where
are the atomic coordinates, and
is the interatomic potential of interaction between atoms
i and
j. For small
N one can hope to enumerate all possible minima and decide the lowest of these, but even for moderate
N and for the simplest
V such as the Lennard–Jones (LJ) potential, this becomes difficult. A case in point is the 38 atom LJ cluster which has the so–called “double funnel” structure; the global minimum, which has octahedral symmetry, is marginally lower than the first excited state which has icosahedral symmetry. These were respectively found by the basin hopping technique [
7] and a genetic algorithm method [
8,
9].
A number of techniques of global optimization have been applied to this problem [
1,
10,
11] and by now there are extensive compilations of global minima for a number of different clusters [
12] , notably those described by two–body or many–body potentials which are commonly applied in atomistic simulations. A major difficulty is in ensuring that the algorithms reach the global minimum without being trapped in local minima. One method of overcoming such trapping [
13] is by transforming the PES, broadening the thermodynamic transitions so as to increase the probability of finding the global minimum at temperatures where the free energy barriers are almost unsurmountable. For example, addition of a linear term to the PES provides a compressing effect which has been shown to be successful in locating the true minima in multiple funneled global structures [
14]. Locatelli and Schoen [
15] used such transformations to locate the global minimum for non-icosahedral clusters.
We have recently proposed a new method of global optimization wherein
time–dependence is introduced in the potential energy landscape [
16]. The evolving landscape is designed in a manner such that asymptotically, the potential energy surface develops into the surface of interest. A number of other techniques can be used to follow the evolving minima. Applications have been made to determining the ground state configurations of simple cluster systems [
16].
In the present paper we apply this method to determine the ground state confi tions and energies of atomic clusters described by the many–body Sutton–Chen potential [
17,
18] by switching from a known ground state. Initially, the interaction is chosen to be the Lennard–Jones potential,
while the surface of interest is the potential
One choice for the time dependent potential energy surface is [
16]
with
g(
t) an adiabatically varying switching function that interpolates between 1 and 0, and
h(
t) doing the reverse.
In the next section we describe the method as applied to the problem of ground state energy determination for Sutton–Chen clusters. Detailed results are presented for one cluster size, while the more general application and results are indicated in brief. This is followed by a discussion and summary.
It is a pleasure to dedicate this article to Steve Berry who has directly and indirectly influenced much of the development in the area of cluster studies over the past few decades. We have learned a lot from him, both in conversation as well as through his many articles and reviews [
19].
2 Adiabatic optimization
The adiabatic optimization method [
16], is a heuristic technique for locating minima. The essential idea is as follows.
Time dependence is introduced into the potential energy landscape directly by the incorporation of slowly varying terms as discussed in Eq. (4). A given choice is made for the switching functions
g(
t) and
h(
t), though in practice the choice does not affect the results greatly. A similar application of the adiabatic principle to determine semiclassical ground states of multidimensional systems [
20] has noted the insensitivity of the technique to the precise form of the switching function, so long as the induced variation of the potential energy surface is slow enough. We note, parenthetically, that the switching principle has wide applicability, and in recent work has been used in the computation of the free–energy of finite clusters [
21].
Location of the evolving minima can be done by any of a number of techniques. The simplest procedure is to introduce damping into the equations of motion and allow the system to evolve to a position of rest in a potential minimum; by starting with an ensemble of initial configurations and varying the available parameters, a number of minima can be located, and the putative global minimum can be recognized. Elsewhere [
16] we have suggested the conjugate gradient [
22] or simulated annealing (SA) [
23] as other possible methods for locating the minima. It is likely that of these, the conjugate gradient technique will be more efficient as compared to SA though some SA variants [
24] may also provide a suitable method for following the evolving minima.
The overall procedure can be summarized as follows:
Take the initial configuration of the
N atom cluster to be the ground state for the LJ
N cluster [
12].
Choose some switching function, say g(t). Similarly choose h(t), and the simplest choice, which we make here, is h(t) = 1 − g(t). We have explored a large variety of switching functions and in the present application we use g(t) = cos2(3πζt) exp(−ζt), where ζ is the adiabaticity parameter.
Perform molecular dynamics simulations for this
N–particle cluster with forces deriving from Eq. (4), with an additional damping term, namely the equations of motion
where
is the position vector for the
kth particle,
m is its mass and
γ is the damping constant.
Vary ζ and γ, keeping in mind the natural timescales of the problem. Evolve to a minimum energy configuration, namely when the particle velocities become zero; the lowest energy found in an ensemble of simulations is the ground state energy predicted by the present method.
2.1 Results for Sutton–Chen global minima
Here we attempt to switch from the minimum of the LJ
N system to the minimum of the SC
N system. Both sets of minima have been extensively studied earlier and are tabulated in the Cambridge Cluster Database [
12]. A point of interest is that for the Sutton-Chen 9-6 family of potentials,[
17,
18] the symmetries of the global minimum configurations are frequently different from the symmetries of the Lennard–Jones minima, so that in the adiabatic switching process, the cluster atoms must also move so as to adopt a different symmetry.
We present detailed results for the cluster size
N = 15, though we have applied this technique to larger clusters and obtained results in agreement with the current standards [
12]. For the 15 atom LJ cluster, the ground state has the point group symmetry C
2v while for the SC cluster the symmetry is D
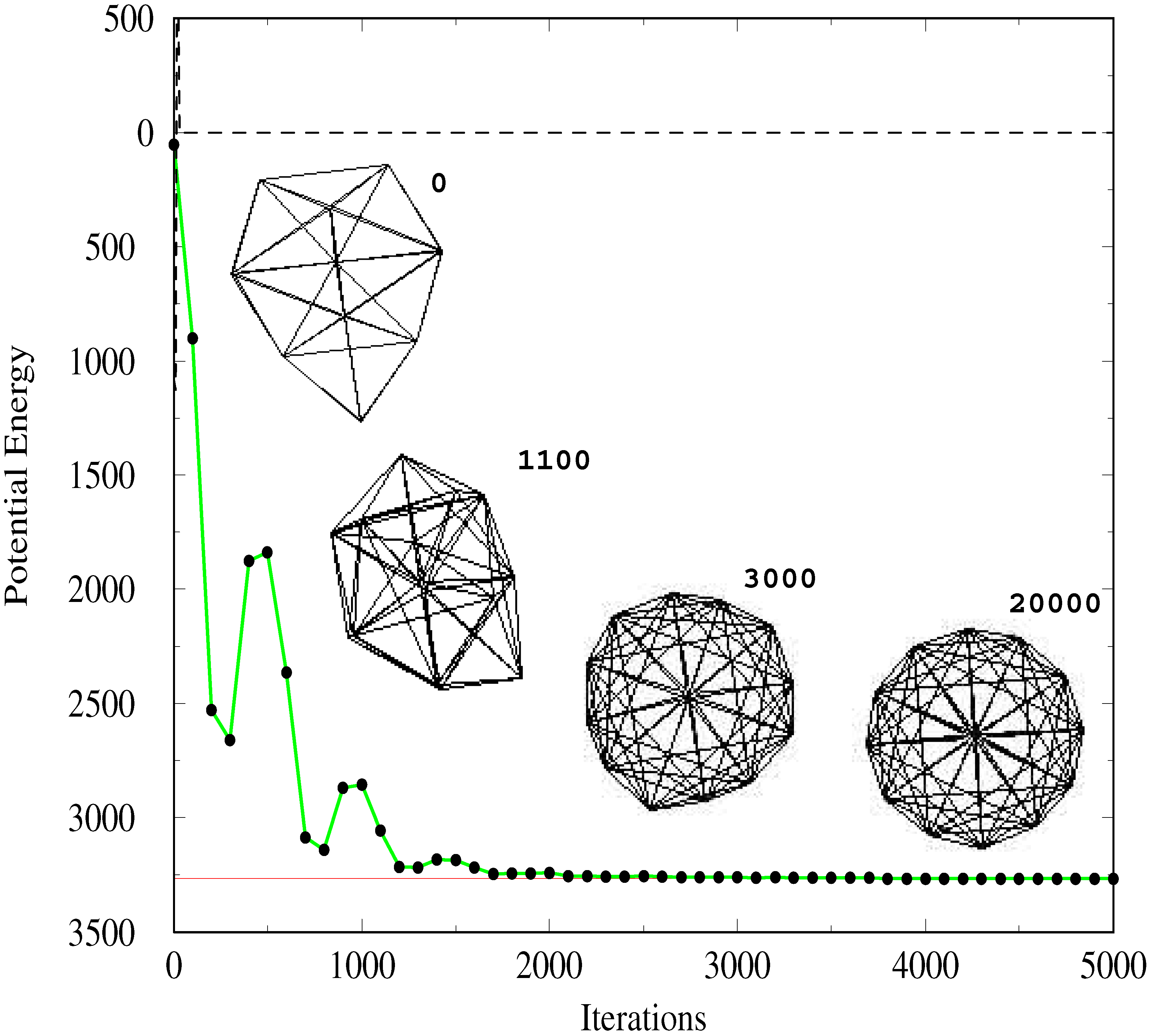
6d. Shown in
Fig. 1 is a plot of the potential energy versus time for a particular choice of
g(
t)
, ζ and
γ. Also shown is the effect of instantaneous switching, namely taking the limit
g(
t) = 0, where it can be seen that the system finds the nearest available local minimum from which it does not move. The time–dependence in the potential effectively permits the system to explore the multidimensional potential energy landscape of the SC cluster in an efficient manner. Finding a local minimum does not trap the system since there is always kinetic energy
until the adiabatic switch is essentially over. Inset in the Figure is a schematic of the cluster configuration at different times during the process, showing how the cluster both contracts as well as rearranges to eventually reach the minimum of the SC surface.
It should be added that we have performed simulations for a variety of cluster sizes and in all cases we find that the procedure successfully finds the tabulated minima of SC clusters; these are not presented here since the details are repetitive. As we have emphasized elsewhere [
16], the present method is heuristic, and thus some exploration of different switching functions, variation in the adiabaticity and damping parameters, and indeed the choice of initial potential,
is necessary.
3 Summary and Discussion
In this paper we have presented the outline of a general procedure for global optimization with specific application to the problem of cluster ground state geometry determination. The application here, to the determination of the minimum of model metallic (Sutton-Chen) clusters by adiabatically deforming the potential energy surface relevant to model rare–gas (Lennard Jones) clusters is meant to be illustrative rather than exhaustive: the method introduced here is one of a class of techniques that employs time–dependence in the potential energy surface to enhance the exploration of phase space in contrast to other means of achieving the same objective [
10].
A multiplicity of techniques is needed to approach hard problems such as global optimization. Few rigorous results are available, and application of most techniques is not guaranteed, with few possible exceptions, to give reliable (or certifiable) results. The present adiabatic switching method locally solves the optimization for an evolving surface, and thus mimics other methods of making large scale excursions in configuration or phase space.
We are presently studying this technique in detail with respect to the variation of parameters as well as to functional variations. One of the main issues of concern, and one that we are addressing in current work, is the relative efficiency of this method in comparison to other global optimization techniques. In a number of applications, we find that this method gives very encouraging results, and permits the determination of fairly reliable minimum energy configurations for a wide variety of cluster systems. The flexibility of choice of a number of starting potentials including the free
Figure 1.
Plot of the potential energy versus iteration number, switching from the Lennard Jones potential to the Sutton Chen. The switching function used is
g(
t) = exp(
−ζt) cos
2(3
πζt) with
ζ = 0.4 and
γ = 0.1. The time step is 0.01 in units natural to the LJ cluster, for which we also take
∊ =
σ = 1. At time
t = 0 the cluster has the C
2v symmetry. At different times, as indicated, the cluster configuration is shown, and asymptotically, the configuration reached is the 9–6 Sutton Chen global minimum, with D
6d symmetry. The parameters used for this latter model are taken from [
12]. The dashed line shows the result of the simulation in the absence of switching, namely when the LJ potential is
suddenly transformed to the Sutton Chen potential.
Figure 1.
Plot of the potential energy versus iteration number, switching from the Lennard Jones potential to the Sutton Chen. The switching function used is
g(
t) = exp(
−ζt) cos
2(3
πζt) with
ζ = 0.4 and
γ = 0.1. The time step is 0.01 in units natural to the LJ cluster, for which we also take
∊ =
σ = 1. At time
t = 0 the cluster has the C
2v symmetry. At different times, as indicated, the cluster configuration is shown, and asymptotically, the configuration reached is the 9–6 Sutton Chen global minimum, with D
6d symmetry. The parameters used for this latter model are taken from [
12]. The dashed line shows the result of the simulation in the absence of switching, namely when the LJ potential is
suddenly transformed to the Sutton Chen potential.
particle case [
16] as well as the flexible choice of switching functions and parameters, and finally the flexibility in the dynamical evolution all combine to suggest that while the method is heuristic, it holds promise.