Quasi-Real Time Estimation of Angular Kinematics Using Single-Axis Accelerometers
Abstract
:1. Introduction
- orientation estimated by time-integrating, from unknown initial conditions, the signals from a triad of mutually orthogonal uni-axial gyros is prone to errors that grow unbounded over time, due to low-frequency gyro bias drifts;
- it is difficult give a simple interpretation to the accelerometer signals, where the component due to the gravity field (vertical reference) coexists with the component related to the motion of the object;
- nearby ferromagnetic materials are critically disturbing sources when attempts are made to interpret the signals from a tri-axial magnetic sensor as the horizontal reference.
2. Experimental Section
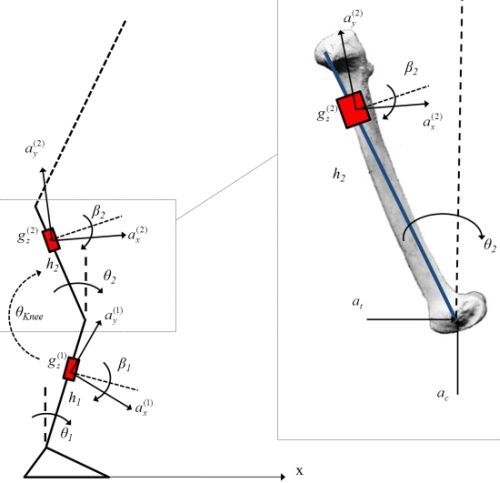
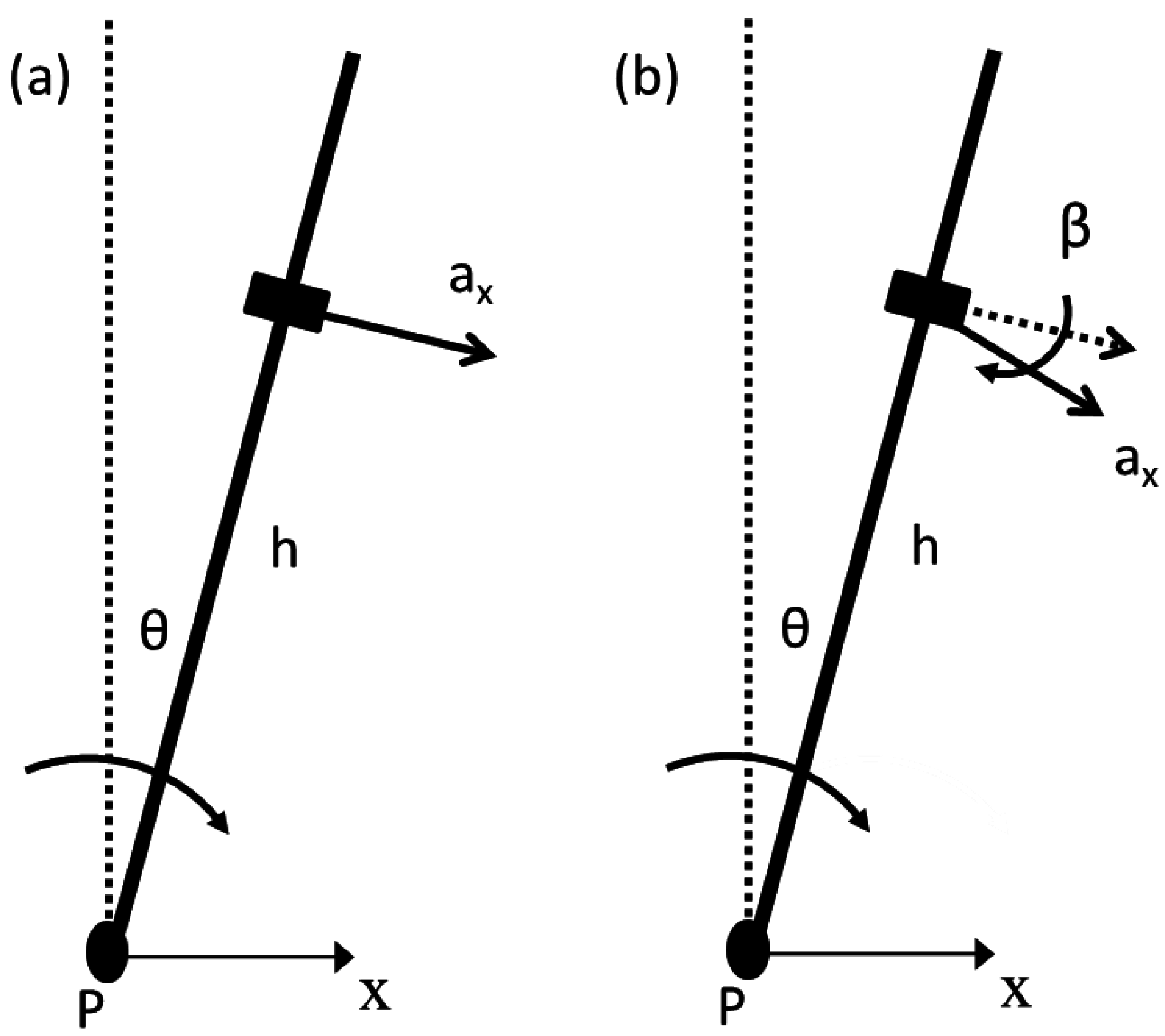
2.1. Inverted Pendulum Kinematics
2.2. Algorithm Overview
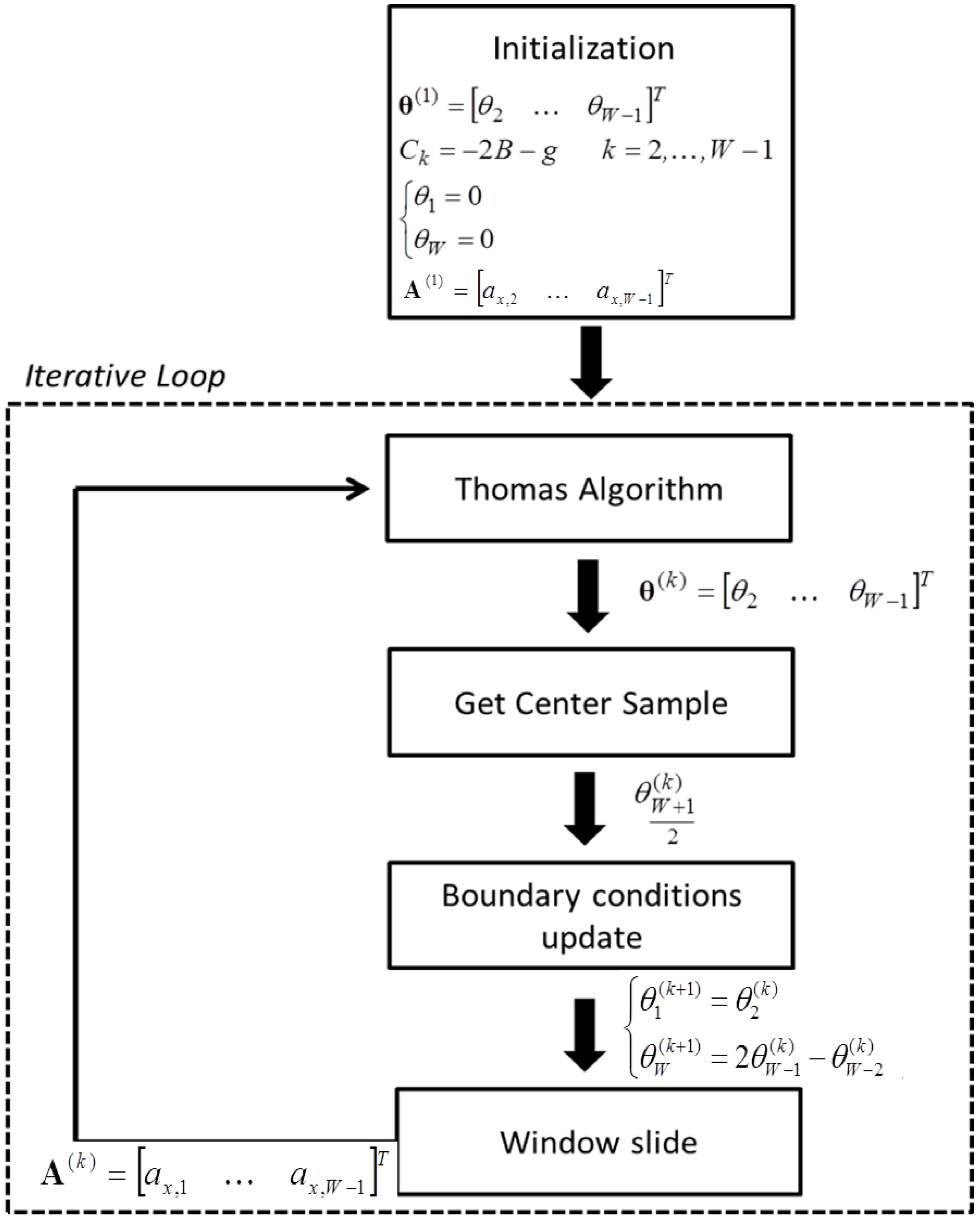
- Initialization: at the first step, Equation (8) is initialized by zeroing the windowed angle vector θ(1) = [θ2, …, θW−1]T and the two boundary conditions (θ1 = 0, θW = 0). The terms on the diagonal of the matrix C are assumed to be constant (Ck = −2B – g, k = 2, …, W − 1) by approximating . The sliding window of the accelerometer output A(1) = [ax,2 …, ax,W−1]T is considered as input.
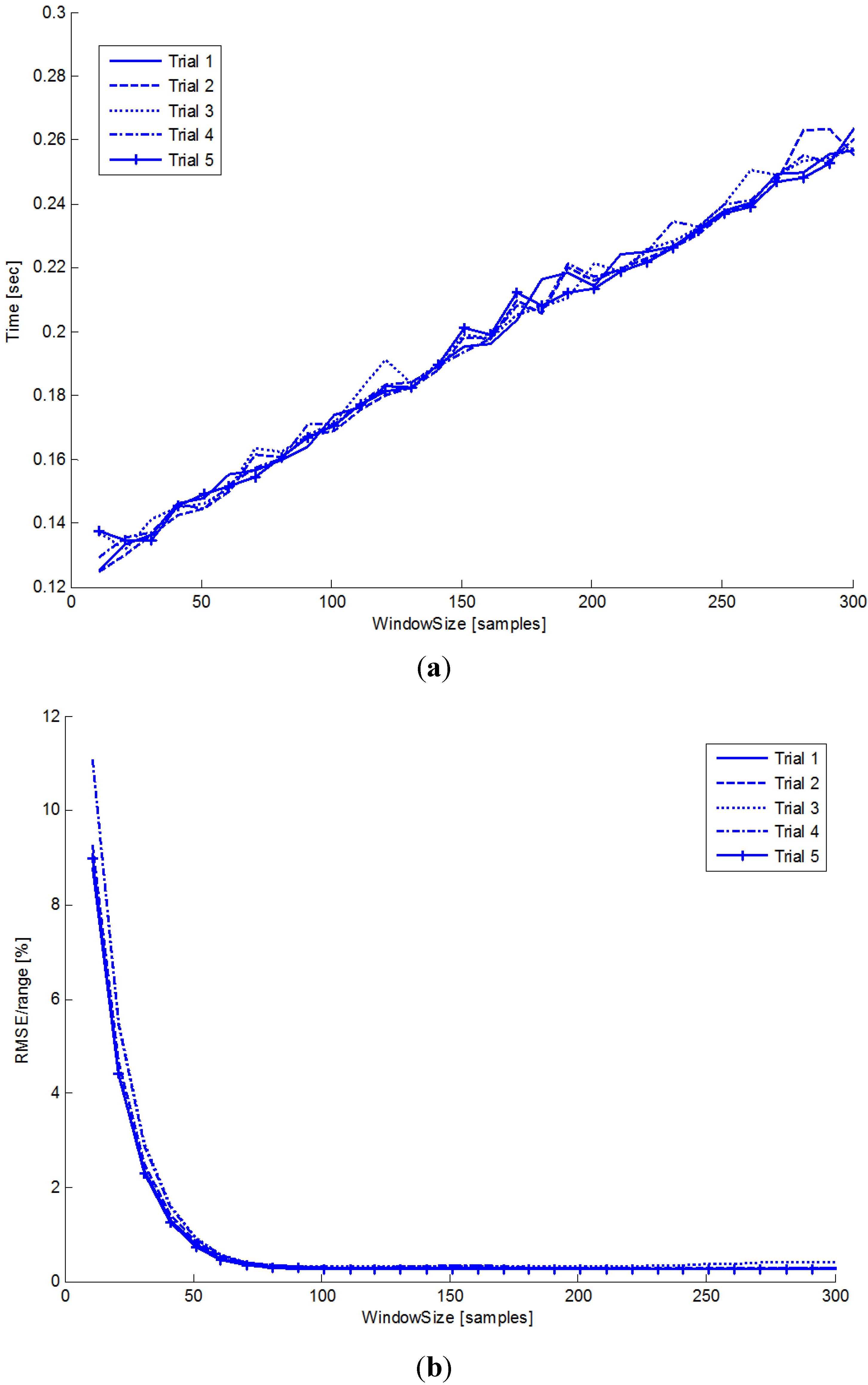
- Thomas algorithm: the sway-angle vector θ(k) is estimated from Equation (8) with I iterations by using the Thomas algorithm [31]. A single iteration is enough to have accurate estimates, except for the first cycle, which requires more iterations (I = 3) to converge because of the initialization process. Increasing the number of iterations I does not significantly improve the estimation accuracy but increases the computational cost.
- Get center sample: as discussed before, at step k, the center sample of the estimated vector θ(k) is considered as correct estimate, under the assumption of adequately large time windows.
- Boundary conditions update: according to the result provided by the Thomas algorithm at the previous step, at step k > 1 the two boundary conditions are set as the first element of the vector θ(k) (left boundary) and as the linear interpolation of the last two elements of the vector θ(k) (right boundary) as follows:The terms of the matrix C are updated with the angle vector elements.
- Window Slide: the input vector A(k) is updated by adding the new sample at the end of the vector and deleting the first one.
2.3. Mechanical Inverted Pendulum
- those obtained by using the offline method proposed in [19], where a bidirectional low-pass filtering of the accelerometer output, with a cut-off frequency depending on the position of the sensor, was implemented;
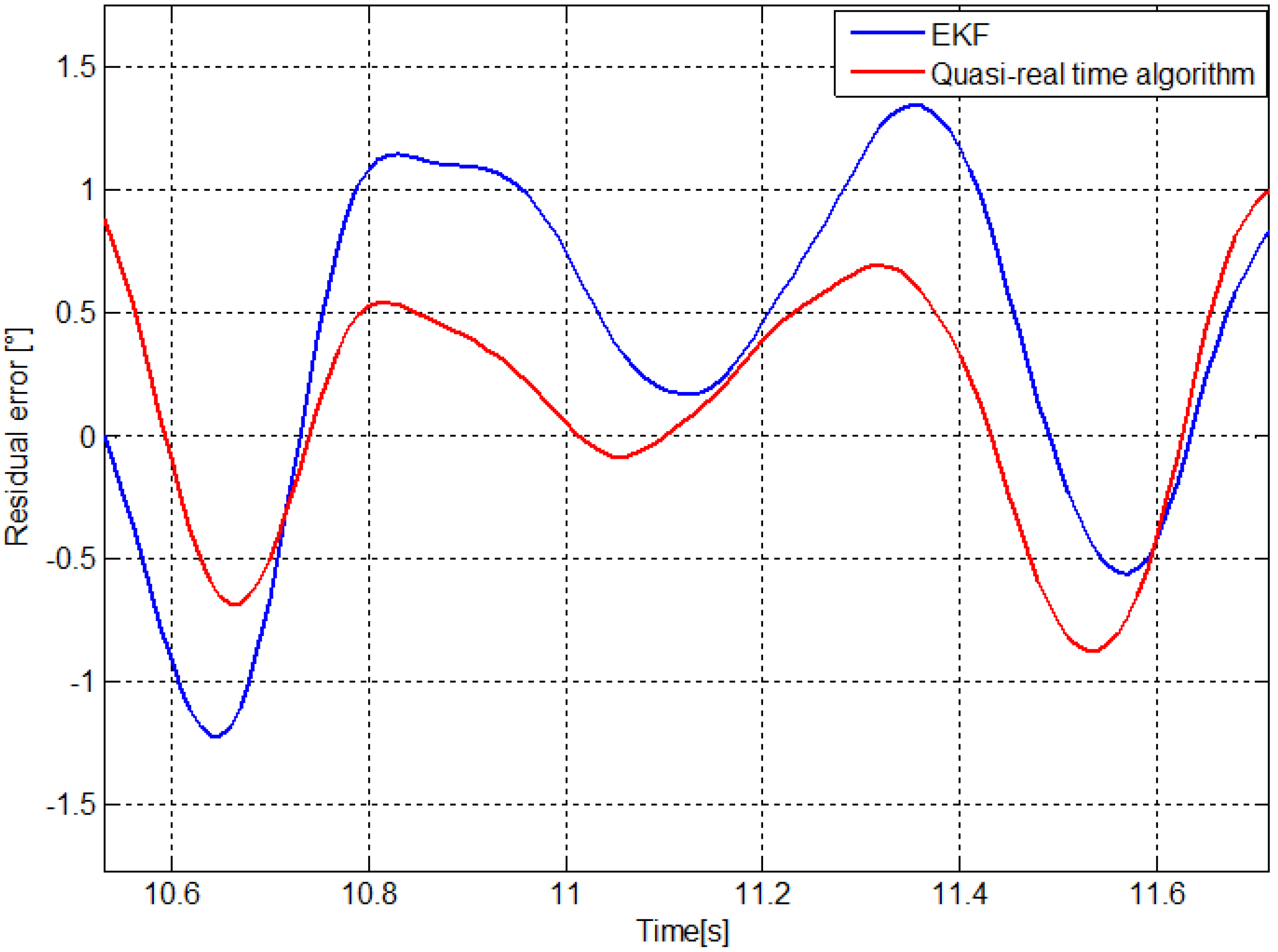
- those obtained by using an EKF applied to the outputs of the IMU (Figure 3), in particular to the accelerometers with sensitive axis orthogonal and along the mechanical arm, ax and ay, and to the output of the gyroscope with sensitive axis orthogonal to the plane of the movement, gz as discussed in the next section.
2.4. Extended Kalman Filter
- ;
- ;
- ;
- ;
- z(k) = ax(k);
- z(k) = ay(k);
- z(k) = gz(k);
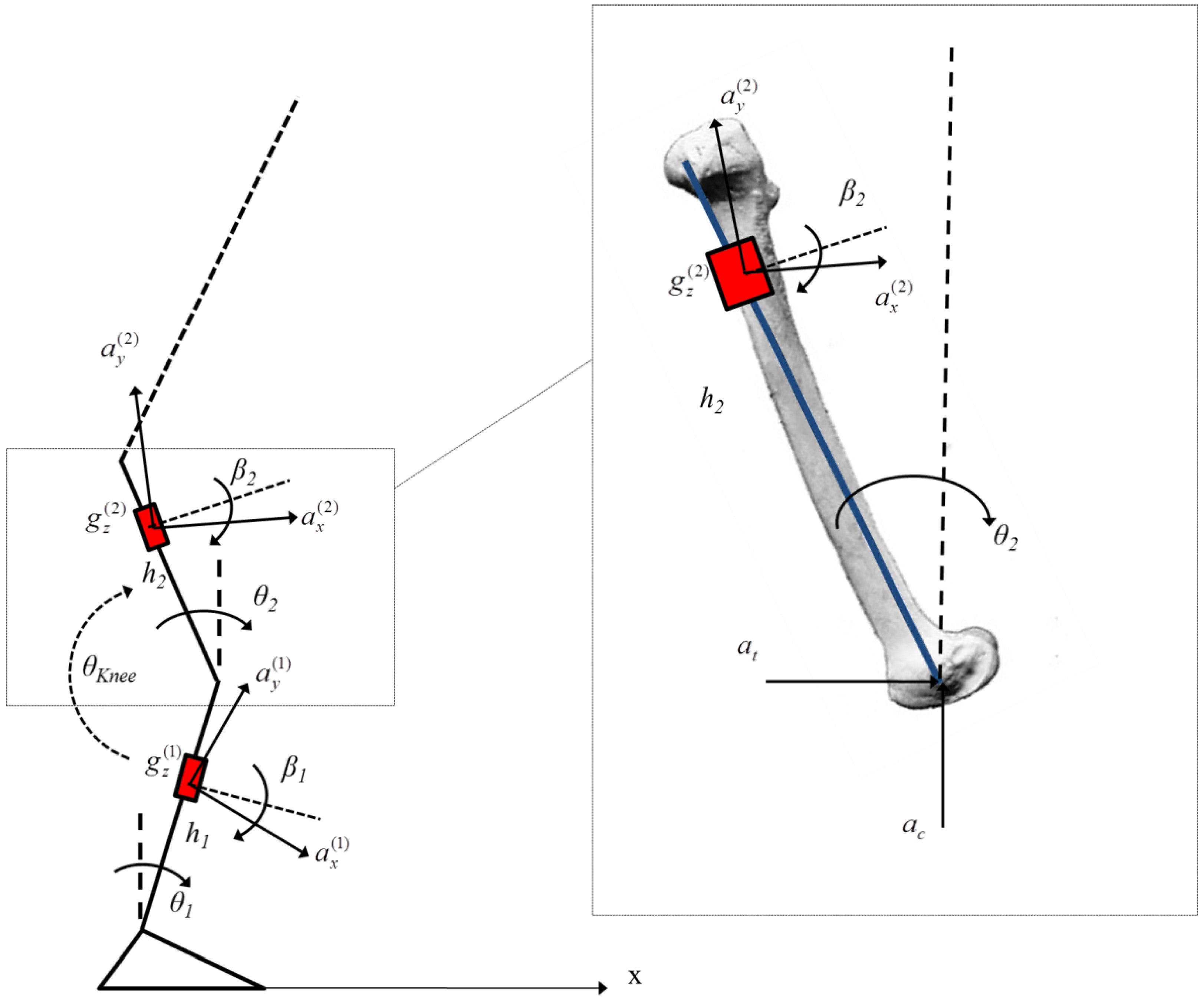
2.5. 2-Link Chain: Knee Flexion-Extension Angle Evaluation
- ;
- ;
- ;
- ;
- ;
- ;
- ;
3. Results
3.1. Mechanical Inverted Pendulum
3.2. Knee Flex-Extension Angle
4. Discussion and Conclusions
Acknowledgments
Appendix A
References
- Landau, L.D.; Lifshitz, E.M. Mechanics, 3rd ed.; Pergamon: New York, NY, USA, 1976; pp. 93–95. [Google Scholar]
- Stocker, J.J. Nonlinear Vibrations in Mechanical and Electrical Systems, 1st ed.; Wiley/Interscience: New York, NY, USA, 1966; pp. 202–213. [Google Scholar]
- Corben, H.C.; Stehele, P. Classical Mechanics, 2nd ed.; Wiley: New York, NY. USA, 1960; pp. 67–69. [Google Scholar]
- Kalmus, H.P. The inverted pendulum. Am. J. Phys. 1978, 38, 874–878. [Google Scholar]
- Michaelis, M.M. Stroboscopic study of the inverted pendulum. Am. J. Phys. 1985, 53, 1079–1083. [Google Scholar]
- Friedman, M.H.; Campana, J.E.; Yergey, A.L. The inverted pendulum: A mechanical analog of the quadrupole mass filter. Am. J. Phys. 1982, 50, 924–931. [Google Scholar]
- Smith, H.J.T.; Blackburn, J.A. Experimental study of an inverted pendulum. Am. J. Phys. 1992, 60, 909–911. [Google Scholar]
- Lee, H.; Jung, S. Balancing and navigation control of a mobile inverted pendulum robot using sensor fusion of low cost sensors. Mechatronics 2012, 22, 95–105. [Google Scholar]
- Sivaraman, E.; Arulselvi, S. Modelling of an inverted pendulum based on fuzzy clustering technique. Int. J. Comp. Appl. 2012, 9, 23–31. [Google Scholar]
- Park, J.H.; Kim, K.D. Biped Robot Walking Using Gravity-Compensated Inverted Pendulum Mode and Computed Torque Control. Proceedings of the 1998 IEEE International Conference on Robotics & Automation, Leuven, Belgium, May 1998.
- Anderson, C.W. Learning to control an inverted pendulum using neural networks. IEEE Contr. Syst. Mag. 1989, 9, 31–37. [Google Scholar]
- Huang, S.J.; Huang, C.L. Control of an inverted pendulum using grey prediction model. IEEE Trans. Ind. Appl. 1994, 36, 452–458. [Google Scholar]
- Loram, I.D.; Lakie, M. Human balancing of an inverted pendulum: Position control by small, ballistic-like, throw and catch movement. J. Physiol. 2002, 540, 1111–1124. [Google Scholar]
- Macpherson, J.M.; Horak, F.B. Posture. In Principles of Neural Science; Kandel, E.R., Schwartz, J.H., Jessell, T.M., Eds.; McGraw-Hill: New York, NY, USA, 2000; Chapter 39. [Google Scholar]
- Guelton, K.; Delprat, S.; Guerra, T.M. An alternative to inverse dynamics joint torques estimation in human stance based on Takagi-Sugeno unknown-inputs observer in the descriptor form. Contr. Eng. Pract. 2008, 16, 1414–1426. [Google Scholar]
- Pinter, I.J.; van Swigchem, R.; van Soest, A.J.; Rozendaal, L.A. The dynamics of postural sway cannot be captured using a one-segment inverted pendulum model: A PCA on segment rotations during unperturbed stance. J. Neurophysiol. 2008, 100, 3197–3208. [Google Scholar]
- Creath, R.; Kiemel, T.; Horak, F.; Peterka, R.; Jeka, J. A unified view of quiet and perturbed stance: simultaneous co-existing excitable modes. Neurosci. Lett. 2005, 377, 75–80. [Google Scholar]
- Fuschillo, V.L.; Bagalà, F.; Chiari, L.; Cappello, A. Accelerometry-based prediction of movement dynamics for balance monitoring. Med. Biol. Eng. Comput. 2012, 50, 925–936. [Google Scholar]
- Bagalà, F.; Fuschillo, V.L.; Chiari, L.; Cappello, A. Calibrated 2D angular kinematics by single-axis accelerometers: From inverted pendulum to n-link chain. IEEE Sens. J. 2012, 12, 479–486. [Google Scholar]
- Sabatini, A.M. Estimating three-dimensional orientation of human body part by inertial/magnetic sensing. Sensors 2011, 11, 1489–1525. [Google Scholar]
- Bagalà, F.; Klenk, J.; Cappello, A.; Chiari, L.; Becker, C.; Lindemann, U. Quantitative description of the Lie-to-Sit-to-Stand-to-Walk transfer by a single body-fixed sensor. IEEE Trans. Neural. Syst. Rehabil. Eng. 2012, in press. [Google Scholar]
- Rotenberg, D.; Slycke, P.J.; Veltink, P.H. Ambulatory position and orientation tracking fusing magnetic and inertial sensing. IEEE Trans. Biomed. Eng. 2007, 54, 883–890. [Google Scholar]
- Cooper, G.; Sheret, I.; McMillian, L.; Siliverdis, K.; Sha, N.; Hodgins, D.; Kenney, L.; Howard, D. Inertial sensor-based knee flexion/extension angle estimation. J. Biomech. 2009, 42, 2678–2685. [Google Scholar]
- Dejnabadi, H.; Jolle, B.M.; Casanova, E.; Fua, P.; Aminian, K. Estimation and visualization of sagittal kinematics of lower limbs orientation using body-fixed sensors. IEEE Trans. Biomed. Eng. 2006, 53, 1385–1393. [Google Scholar]
- Kamen, G.; Patten, C.; Duke, D.C.; Sison, S. An accelerometry-based system for the assessment of balance and postural sway. Gerontology 1998, 44, 40–45. [Google Scholar]
- Moe-Nilssen, R. A new method for evaluating motor control in gait under real-life environmental conditions. Part 1: The instrument. Clin. Biomech. 1998, 13, 320–327. [Google Scholar]
- Mayagoitia, R.E.; Lötters, J.C.; Veltink, P.H.; Hermens, H. Standing balance evaluation using a triaxial accelerometer. Gait Posture 2002, 16, 55–59. [Google Scholar]
- Mayagoitia, R.E.; Nene, A.V.; Veltink, P.H. Accelerometer and rate gyroscope measurement of kinematics: An inexpensive alternative to optical motion analysis systems. J. Biomech. 2002, 35, 537–542. [Google Scholar]
- Lyons, G.M.; Culhane, K.M.; Hilton, D.; Grace, P.A.; Lyons, D. A description of an accelerometer-based mobility monitoring technique. Med. Eng. Phys. 2005, 27, 497–504. [Google Scholar]
- Williamson, R.; Andrews, B.J. Detecting absolute human knee angle and angular velocity using accelerometers and rate gyroscopes. Med. Biol. Eng. Comput. 2001, 39, 1–9. [Google Scholar]
- Thomas, L.H. Elliptic Problems in Linear Differential Equations over a Network; Watson Science Computer Laboratory Report; Columbia University: New York, NY, USA, 1949. [Google Scholar]
- Kalman, R. A new approach to linear filtering and prediction problems. Trans. ASME 1960, 82, 35–45. [Google Scholar]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter; University of North Carolina at Chapel Hill: Chapel Hill, CA, USA, 1995. [Google Scholar]
- Salem, G.J.; Salinas, R.; Harding, F.V. Bilateral kinematic and kinetic analysis of the squat exercise after anterior cruciate ligament reconstruction. Archive Phys. Med. Rehab. 2003, 84, 1211–1216. [Google Scholar]
- Arun, K.; Huang, T.; Blostein, S. Least-squares fitting of two 3-D point sets. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 9, 698–700. [Google Scholar]
- Hanson, R.; Norris, M. Analysis of measurements based on the singular value decomposition. SIAM J. Sci. Stat. Comp. 1981, 2, 363–373. [Google Scholar]


| Tested algorithms | RMSE [°] mean ± std |
|---|---|
| Quasi-real time algorithm | 0.40 ± 0.02 |
| Bagalàet al. algorithm [19] | 0.39 ± 0.05 |
| EKF: | 0.45 ± 0.05 |
| EKF: | 0.46 ± 0.05 |
| EKF: | 2.12 ± 0.15 |
| EKF: | 20.64 ± 12.48 |
| EKF: z(k) = ax(k) | 26.71 ± 0.70 |
| EKF: z(k) = ay(k) | 41.83 ± 7.50 |
| EKF: z(k) = gz(k) | 8.87 ± 6.92 |
| Tested algorithms | RMSE [°] mean ± std |
|---|---|
| Quasi-real time algorithm | 1.01 ± 0.11 |
| Bagalà et al. algorithm [19] | 0.95 ± 0.48 |
| EKF: | 2.43 ± 0.76 |
| EKF: | 2.46 ± 0.62 |
| EKF: | 2.83 ± 0.24 |
| EKF: | 37.13 ± 18.28 |
| EKF: z(k) = ax(k) | 19.31 ± 0.64 |
| EKF: z(k) = ay(k) | 43.27 ± 5.05 |
| EKF: z(k) = gz(k) | 3.95 ± 2.59 |
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Caroselli, A.; Bagalà, F.; Cappello, A. Quasi-Real Time Estimation of Angular Kinematics Using Single-Axis Accelerometers. Sensors 2013, 13, 918-937. https://doi.org/10.3390/s130100918
Caroselli A, Bagalà F, Cappello A. Quasi-Real Time Estimation of Angular Kinematics Using Single-Axis Accelerometers. Sensors. 2013; 13(1):918-937. https://doi.org/10.3390/s130100918
Chicago/Turabian StyleCaroselli, Alessio, Fabio Bagalà, and Angelo Cappello. 2013. "Quasi-Real Time Estimation of Angular Kinematics Using Single-Axis Accelerometers" Sensors 13, no. 1: 918-937. https://doi.org/10.3390/s130100918