Colloidal Stability and Magnetic Field-Induced Ordering of Magnetorheological Fluids Studied with a Quartz Crystal Microbalance
Abstract
:1. Introduction
2. Background on High-Frequency Contact Mechanics

3. Experimental Section
3.1. Experimental Set-Up
- −
- A QCM cell containing an AT-cut quartz crystal provided by CH Instruments Inc. (Austin, TX, USA, 7.995 MHz fundamental frequency, 13.7 mm blank diameter, 5.1 mm electrode diameter, polished surface finish, 100 Å Ti and 1000 Å Au electrode material, keyhole electrode pattern).
- −
- 200 MHz (−3 dB) Panametric ultrasonic pulser/receiver, model 5900 PR (P/R mode, 2 kHz PRF, 1 μJ energy, 50 Ω damping, 1 MHz HP filer, 200 MHz LP filter, 0 dB attenuators, 40 dB gain, 0˚ RF output phase).
- −
- 500 MHz, 4 GSa/s, DS4054 Rigol, digitizing oscilloscope (150,000 acquisition points).
- −
- Personal computer connected to the oscilloscope via USB interface.

3.2. Signal Processing


3.3. MR Fluid Characteristics
- −
- The sample “OM MRF” is the homemade suspension. It consists of carbonyl iron microparticles (OM grade from BASF SE, mean diameter 5 μm) dispersed in a highly-viscous silicone oil (487 mPa·s, Sigma-Aldrich, St, Louis, MO, USA). The particle content was 5 vol%. This formulation does not include additives. The density of the suspensions at 25 °C was 1126 ± 10 kg/m3. The viscosity of the OM MRF measured with the rotational shear rheometer at a temperature of 25 °C and a shear rate of 100 s−1 was 515 ± 15 mPa·s.
- −
- The sample “Commercial MRF” (reference MRF-132 supplied by Lord Corporation, Carrey, NC, USA) consists of iron particles with a diameter between 5 to 10 μm suspended in a carrier fluid. The particle volume fraction is 32 vol%. In this case, (proprietary) thixotropic additives prevent short-term sedimentation. According to the manufacturer, the density of the suspension at 25 °C is 3050 ± 100 kg/m3. The viscosity of the commercial MRF measured with the rotational shear rheometer at a temperature of 25 °C and a shear rate of 100 s−1 was 300 ± 50 mPa·s.
| MR Fluids | Density kg/m3 | Viscosity mPas | Vol. Fraction | Thixotropic Additives | Carrier Liquid | Particles | |
|---|---|---|---|---|---|---|---|
| OM_MR | b 1126 ± 10 | b 515 ± 15 | 5% | NO | Silicone oil | Grade | OM |
| Coating | None | ||||||
| Diameter | 5 µm | ||||||
| Bulk composition | Fe(>97.8%), C(0.7%–0.9%), N(0.6%–0.9%), O(0.2%–0.4%) | ||||||
| Commercial MRF | a 3050 ± 100 | b 300 ± 50 | 32% | YES | Hydrocarbon | Grade | Unknown |
| Coating | YES | ||||||
| Diameter | 5–10 µm | ||||||
| Bulk composition | Unknown | ||||||
4. Results and Discussion
4.1. Sedimentation



4.2. Effects of Magnetic Fields



4.3. Finite Element Modeling
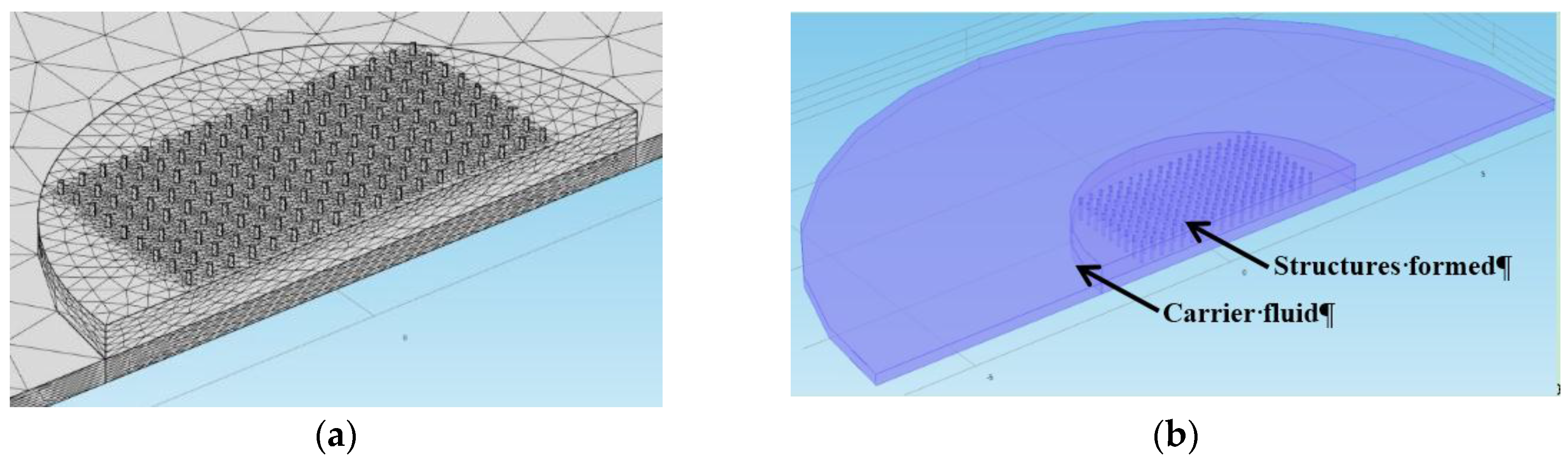
| Description | Δfr FEM Results |
|---|---|
| Magnetic field applied | 950 Hz |
| Sedimentation | −1000 Hz |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lane, T.J. Ultrasonic rheology of mixed-phase systems: Using a QCM as an effective rheological device-theory and applications for combined surface and bulk rheology. ACS Symp. Ser. 2011, 1070, 145–174. [Google Scholar]
- Reviakine, I.; Johannsmann, D.; Richter, R.P. Hearing what you cannot see and visualizing what you hear: Interpreting quartz crystal microbalance data from solvated interfaces. Anal. Chem. 2011, 83, 8838–8848. [Google Scholar] [CrossRef] [PubMed]
- Johannsmann, D. The Quartz Crystal Microbalance in Soft Matter Research; Springer International Publishing: Gewerbestrasse, Switzerland, 2015. [Google Scholar]
- Lu, C.; Czanderna, A.W. Applications of Piezoelectric Quartz Crystal Microbalances; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Nomura, T.; Okuhar, A.M. Frequency shifts of piezoelectric quartz crystals immersed in organic liquids. Anal. Chim. Acta 1982, 142, 281–284. [Google Scholar] [CrossRef]
- Dultsev, F.N.; Tronin, A.V. Rapid sensing of hepatitis B virus using QCM in the thickness shear mode. Sens. Actuators B Chem. 2015, 216, 1–5. [Google Scholar] [CrossRef]
- Höök, F.; Rodahl, M.; Brzezinski, P.; Kasemo, B. Energy dissipation kinetics for protein and antibody-antigen adsorption under shear oscillation on a quartz crystal microbalance. Langmuir 1998, 14, 729–734. [Google Scholar] [CrossRef]
- Kurth, D.G.; Bein, T. Surface reactions on thin layers of silane coupling agents. Langmuir 1993, 9, 2965–2973. [Google Scholar] [CrossRef]
- Marx, K.A. Quartz crystal microbalance: A useful tool for studying thin polymer films and complex biomolecular systems at the solution—Surface interface. Biomacromolecules 2003, 4, 1099–1120. [Google Scholar] [CrossRef] [PubMed]
- O’Sullivan, C.K.; Guilbault, G.G. Commercial quartz crystal microbalances—Theory and applications. Biosens. Bioelectron. 1999, 14, 663–670. [Google Scholar] [CrossRef]
- Johannsmann, D. Feature Article Viscoelastic analysis of organic thin films on quartz resonators. Macromol. Chem. Phys. 1999, 200, 501–516. [Google Scholar] [CrossRef]
- Dybwad, G.L. A sensitive new method for the determination of adhesive bonding between a particle and a substrate. J. Appl. Phys. 1985, 58, 2789–2790. [Google Scholar] [CrossRef]
- Laschitsch, A.; Johannsmann, D. High frequency tribological investigations on quartz resonator surfaces. J. Appl. Phys. 1999, 85, 3759–3765. [Google Scholar] [CrossRef]
- Bossis, G.; Lacis, S.; Meunier, A.; Volkova, O. Magnetorheological fluids. J. Magn. Magn. Mater. 2002, 252, 224–228. [Google Scholar] [CrossRef]
- De Vicente, J.; Klingenberg, D.J.; Hidalgo-Alvarez, R. Magnetorheological fluids: A review. Soft Matter 2011, 7, 3701–3710. [Google Scholar] [CrossRef]
- Ido, Y.; Inagaki, T.; Yamaguchi, T. Numerical simulation of microstructure formation of suspended particles in magnetorheological fluids. J. Phys. Condens. Matter 2010, 22. [Google Scholar] [CrossRef] [PubMed]
- Mohebi, M.; Jamasbi, N.; Liu, J. Simulation of the formation of nonequilibrium structures in magnetorheological fluids subject to an external magnetic field. Phys. Rev. E 1996, 54, 5407–5413. [Google Scholar] [CrossRef]
- Fernández-Toledano, J.C.; Rodríguez-López, J.; Shahrivar, K.; Hidalgo-Álvarez, R.; Elvira, L.; Montero de Espinosa, F.; de Vicente, J. Two-step yielding in magnetorheology. J. Rheol. 2014, 58, 507–534. [Google Scholar]
- Carlson, J.D.; Sproston, J.L. Controllable Fluids in 2000-Status of ER and MR Fluid Technology. In Proceedings of the Actuator 2000–7th International Conference on New Actuators, Bremen, Germany, 19–21 June 2000; pp. 126–130.
- Klingenberg, D.J. Magnetorheology: Applications and challenges. AIChE J. 2001, 47, 246–249. [Google Scholar] [CrossRef]
- Olabi, A.G.; Grunwald, A. Design and application of magneto-rheological fluid. Mater. Des. 2007, 28, 2658–2664. [Google Scholar] [CrossRef] [Green Version]
- Johannsmann, D.; Mathauer, K.; Wegner, G.; Knoll, W. Viscoelastic properties of thin films probed with a quartz-crystal resonator. Phys. Rev. B 1992, 46, 7808–7815. [Google Scholar] [CrossRef]
- D’Amour, J.N.; Stålgren, J.J.R.; Kanazawa, K.K.; Frank, C.W.; Rodahl, M.; Johannsmann, D. Capillary Aging of the Contacts between Glass Spheres and a Quartz Resonator Surface. Phys. Rev. Lett. 2006, 96. [Google Scholar] [CrossRef] [PubMed]
- Olsson, A.L.J.; van Der Mei, H.C.; Johannsmann, D.; Busscher, H.J.; Sharma, P.K. Probing colloid-substratum contact stiffness by acoustic sensing in a liquid phase. Anal. Chem. 2012, 84, 4504–4512. [Google Scholar] [CrossRef] [PubMed]
- Pomorska, A.; Shchukin, D.; Hammond, R.; Cooper, M.A.; Grundmeier, G.; Johannsmann, D. Positive frequency shifts observed upon adsorbing micron-sized solid objects to a quartz crystal microbalance from the liquid phase. Anal. Chem. 2010, 82, 2237–2242. [Google Scholar] [CrossRef] [PubMed]
- Vittorias, E.; Kappl, M.; Butt, H.J.; Johannsmann, D. Studying mechanical microcontacts of fine particles with the quartz crystal microbalance. Powder Technol. 2010, 203, 489–502. [Google Scholar] [CrossRef]
- Resa, P.; Castro, P.; Rodríguez-López, J.; Elvira, L. Broadband spike excitation method for in-liquid QCM sensors. Sens. Actuators B Chem. 2012, 166/167, 275–280. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Lopez, J.; Elvira, L.; Montero de Espinosa Freijo, F.; Bossis, G.; de Vicente, J. Measuring the yield stress in magnetorheological fluids using ultrasounds. Appl. Phys.Lett. 2013, 102. [Google Scholar] [CrossRef] [Green Version]
- Johannsmann, D. Viscoelastic, mechanical, and dielectric measurements on complex samples with the quartz crystal microbalance. Phys. Chem. 2008, 10, 4516–4534. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodriguez-López, J.; Castro, P.; De Vicente, J.; Johannsmann, D.; Elvira, L.; Morillas, J.R.; Montero de Espinosa, F. Colloidal Stability and Magnetic Field-Induced Ordering of Magnetorheological Fluids Studied with a Quartz Crystal Microbalance. Sensors 2015, 15, 30443-30456. https://doi.org/10.3390/s151229808
Rodriguez-López J, Castro P, De Vicente J, Johannsmann D, Elvira L, Morillas JR, Montero de Espinosa F. Colloidal Stability and Magnetic Field-Induced Ordering of Magnetorheological Fluids Studied with a Quartz Crystal Microbalance. Sensors. 2015; 15(12):30443-30456. https://doi.org/10.3390/s151229808
Chicago/Turabian StyleRodriguez-López, Jaime, Pedro Castro, Juan De Vicente, Diethelm Johannsmann, Luis Elvira, Jose R. Morillas, and Francisco Montero de Espinosa. 2015. "Colloidal Stability and Magnetic Field-Induced Ordering of Magnetorheological Fluids Studied with a Quartz Crystal Microbalance" Sensors 15, no. 12: 30443-30456. https://doi.org/10.3390/s151229808
APA StyleRodriguez-López, J., Castro, P., De Vicente, J., Johannsmann, D., Elvira, L., Morillas, J. R., & Montero de Espinosa, F. (2015). Colloidal Stability and Magnetic Field-Induced Ordering of Magnetorheological Fluids Studied with a Quartz Crystal Microbalance. Sensors, 15(12), 30443-30456. https://doi.org/10.3390/s151229808








