Immunity to Laser Power Variation in a DFB Diode Laser Based Optical Gas Sensor Using a Division Process
Abstract
:1. Introduction
2. RAM Suppression in WMS Detection
2.1. Harmonic Signals Analysis
2.2. Improvement Test with the Division Process


| Normalized Features | Single Beam | Division Process |
|---|---|---|
| Bias | 38.70% | 1.20% |
| Baseline Difference | 2.70% | 0.69% |
| Asymmetry | 15.40% | 0.22% |

3. Laser Power Instability Suppression in WMS Detection

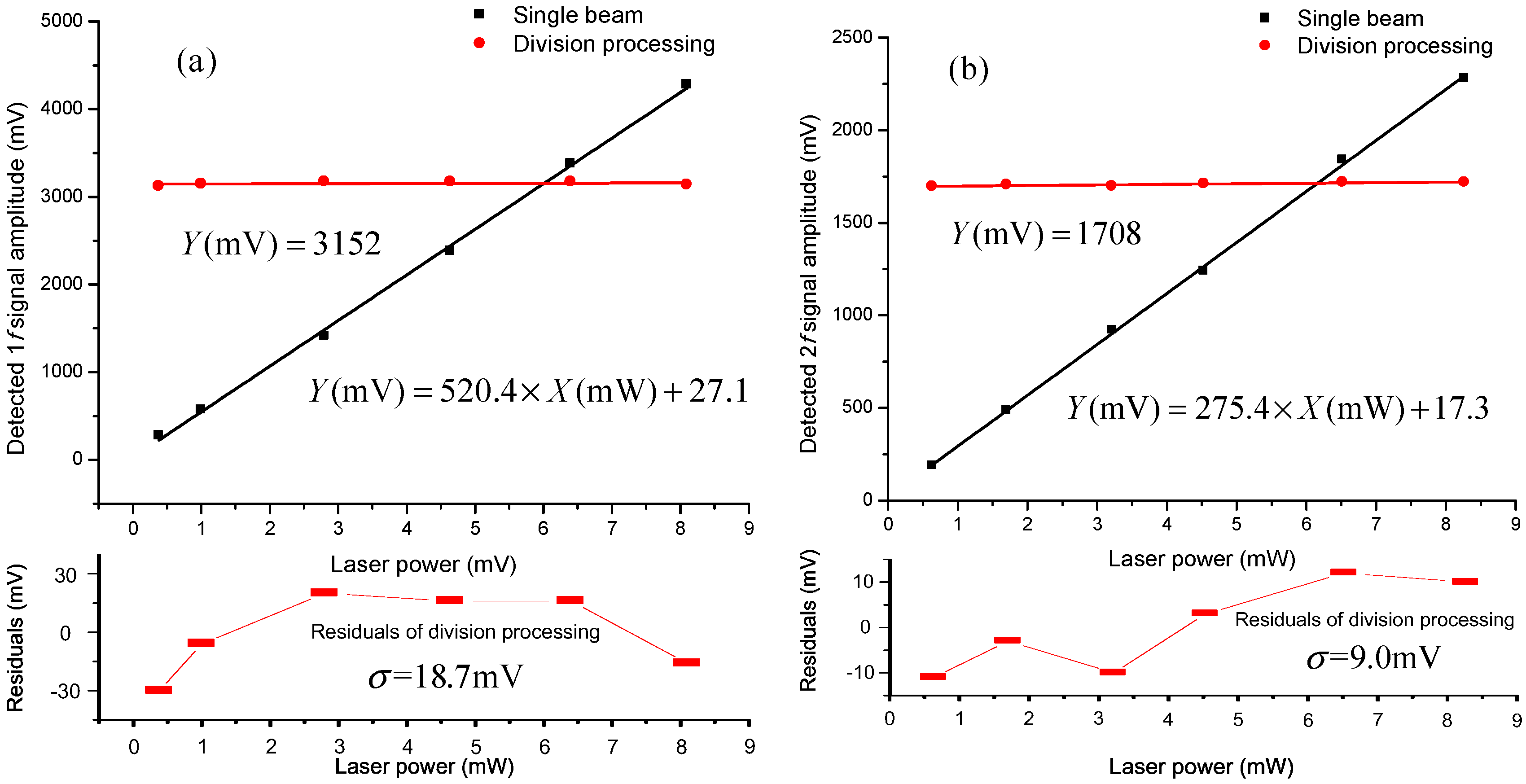
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, H.; Wang, Q.; Chang, J.; Zhang, X.; Zhang, S.; Ni, J. Measurement technique for methane concentration by wavelength scanning of a distributed-feedback laser. Laser Phys. 2008, 18, 491–494. [Google Scholar] [CrossRef]
- Wang, Q.; Chang, J.; Kong, D.L.; Liu, Y.N.; Wang, F.P.; Zhu, C.G.; Wei, W.; Liu, X.Z. Optical measurement of water vapor concentration and gas pressure. IEEE Sens. J. 2014, 14, 563–569. [Google Scholar] [CrossRef]
- De Tommasi, E.; Casa, G.; Gianfrani, L. An intensity-stabilized diode-laser spectrometer for sensitive detection of NH3. IEEE T. Instrum. Meas. 2007, 56, 309–313. [Google Scholar]
- Rothman, L.S.; Gordon, I.E.; Babikov, Y.; Barbe, A.; Chris Benner, D.; Bernath, P.F.; Birk, M.; Bizzocchi, L.; Boudon, V.; Brown, L.R.; et al. The HITRAN2012 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transfer 2013, 130, 4–50. [Google Scholar] [CrossRef]
- Duffin, K.; McGettrick, A.J.; Johnstone, W.; Stewart, G.; Moodie, D.G. Tunable diode laser spectroscopy with wavelength modulation: a calibration-free approach to the recovery of absolute gas absorption line shapes. J. Lightwave Technol. 2007, 25, 3114–3125. [Google Scholar] [CrossRef]
- Asakawa, T.; Kanno, N.; Tonokura, K. Diode Laser Detection of Greenhouse Gases in the Near-Infrared Region by Wavelength Modulation Spectroscopy: Pressure Dependence of the Detection Sensitivity. Sensors 2010, 10, 4686–4699. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Chang, J.; Zhu, C.-G.; Li, C.; Song, F.-J.; Liu, Y.-N.; Liu, X.-Z. Detection of water vapor concentration based on differential value of two adjacent absorption peaks. Laser Phys. Lett. 2012, 9, 421–425. [Google Scholar] [CrossRef]
- Richter, D.; Lancaster, D.G.; Tittel, F.K. Development of an automated diode laser based multi-component gas sensor. Appl. Opt. 2000, 39, 4444–4450. [Google Scholar] [CrossRef] [PubMed]
- Gabrysh, M.; Corsi, C.; Pavone, F.S.; Inguscio, M. Simultaneous detection of CO and CO2 using a semiconductor DFB diode laser at 1.578 μm. Appl. Phys. B 1997, 65, 75–79. [Google Scholar] [CrossRef]
- Schilt, S.; Thevenaz, L.; Robert, P. Wavelength modulation spectroscopy: Combined frequency and intensity laser modulation. Appl. Opt. 2003, 42, 6728–6738. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Chang, J.; Wang, Z.; Tian, C.; Jiang, S.; Lv, G. Study of an optical fiber water vapor sensor based on a DFB diode laser: Combined wavelength scanning and intensity modulation. J. Mod. Opt. 2014, 61, 1538–1544. [Google Scholar] [CrossRef]
- Klein, A.; Witzel, O.; Ebert, V. Rapid, Time-Division Multiplexed, Direct Absorption and Wavelength Modulation-Spectroscopy. Sensors 2014, 14, 21497–21513. [Google Scholar] [CrossRef] [PubMed]
- Haller, K.L.; Hobbs, P.C.D. Double beam laser absorption spectroscopy: Shot-Noise-Limited performance at baseband with a novel electronic noise canceller. Proc. SPIE 1991, 1435, 298–309. [Google Scholar]
- Philippe, L.C.; Hanson, R.K. Laser diode wavelength-modulation spectroscopy for simultaneous measurement of temperature, pressure, and velocity in shock-heated oxygen flows. Appl. Opt. 1993, 32, 6090–6103. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, H.; Chang, J.; Huang, Q.; Wang, Q.; Tian, C.; Wei, W.; Liu, Y. Immunity to Laser Power Variation in a DFB Diode Laser Based Optical Gas Sensor Using a Division Process. Sensors 2015, 15, 9582-9591. https://doi.org/10.3390/s150409582
Chang H, Chang J, Huang Q, Wang Q, Tian C, Wei W, Liu Y. Immunity to Laser Power Variation in a DFB Diode Laser Based Optical Gas Sensor Using a Division Process. Sensors. 2015; 15(4):9582-9591. https://doi.org/10.3390/s150409582
Chicago/Turabian StyleChang, Hengtai, Jun Chang, Qingjie Huang, Qiang Wang, Changbin Tian, Wei Wei, and Yuanyuan Liu. 2015. "Immunity to Laser Power Variation in a DFB Diode Laser Based Optical Gas Sensor Using a Division Process" Sensors 15, no. 4: 9582-9591. https://doi.org/10.3390/s150409582
APA StyleChang, H., Chang, J., Huang, Q., Wang, Q., Tian, C., Wei, W., & Liu, Y. (2015). Immunity to Laser Power Variation in a DFB Diode Laser Based Optical Gas Sensor Using a Division Process. Sensors, 15(4), 9582-9591. https://doi.org/10.3390/s150409582






