A Multi-Hop Energy Neutral Clustering Algorithm for Maximizing Network Information Gathering in Energy Harvesting Wireless Sensor Networks
Abstract
:1. Introduction
- First, we propose a Multi-hop Energy Neutral Clustering (MENC) algorithm that ensures the network-wide energy neutral operation. MENC clusters the network with goal of providing perpetual network operation by controlling the network data transmission rate and selecting the qualified CHs based on the available energy of sensor nodes.
- Second, we construct an easy-to-deploy network architecture in which the sensor field is divided into several ring-based units, and CHs in different units compose a multi-hop routing backbone. Based on this network architecture, we analyze the energy consumption of sensor nodes for intra- and inter-cluster data transmission and then give the energy neutrality constraints. Under these constraints, every sensor node can work in an energy neutral state.
- Third, by balancing the average energy consumption of nodes in different units, we conclude a constraint formula of the number of clusters between neighbor units. Under this constraint, we can avoid packet loss problem which is caused by the limited data forwarding ability of the CHs in the unit closer to BS.
- At last, under the energy neutrality constraints, we optimize the parameters appeared in our proposed protocol through convex optimization, including the optimal number of units, minimum network data transmission cycle and number of clusters in the first unit, for the purpose of maximizing network information gathering.
2. Related Works
3. System Model and Problem Statement
3.1. Sensor and Network Model

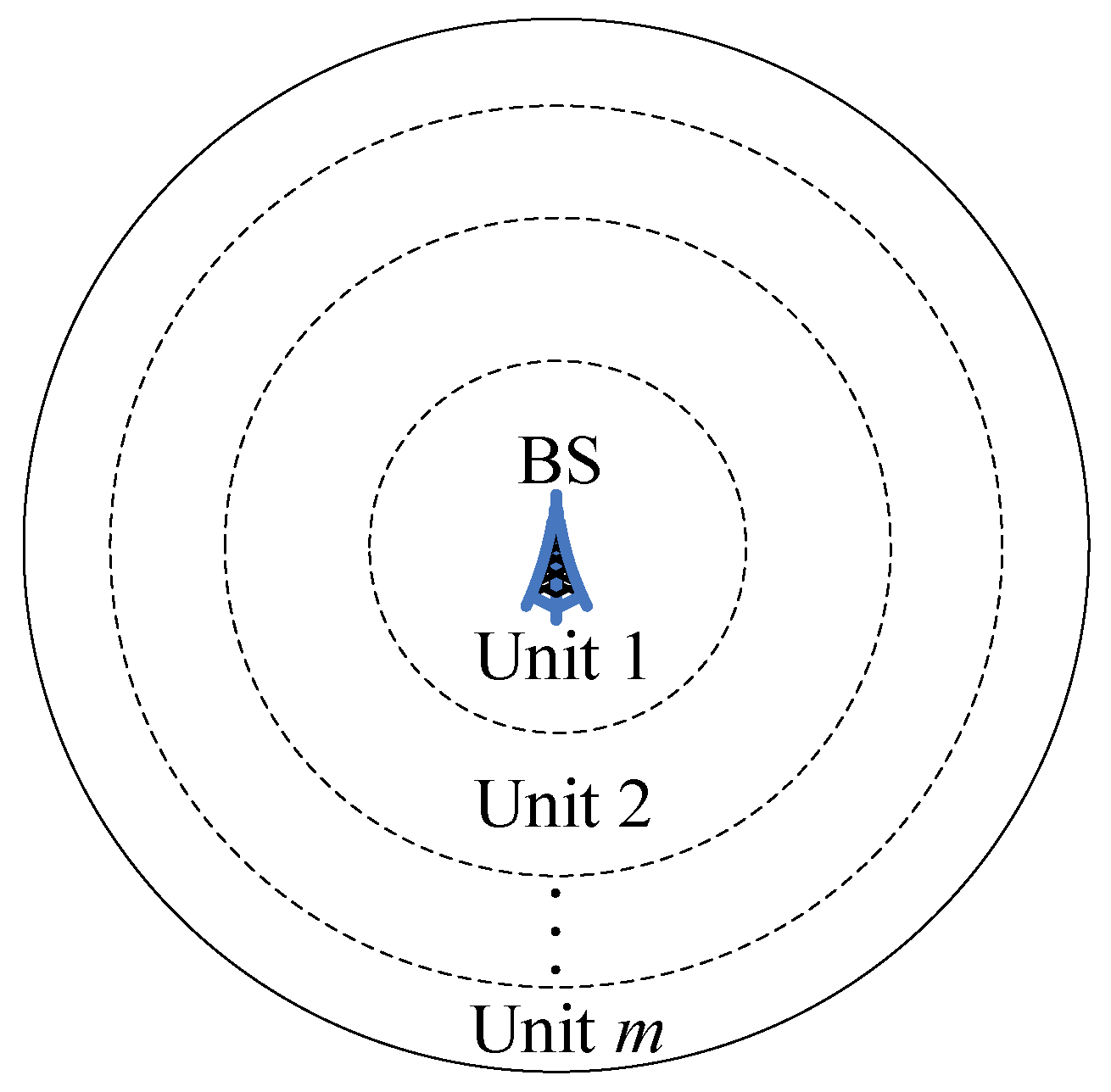
- All EH-Sensors are homogeneous and have the same ability to harvest energy from the ambient environment;
- Each EH-Sensor is stationary or nearly stationary after deployed in the sensor field;
- Each EH-Sensor can estimate the distance to the transmitter according to the received signal strength indicator (RSSI), if the transmitting power is known in advance;
- Each EH-Sensor can adjust its communication power level according to the distance to the expected destination;
- If an EH-Sensor serves as a CH, it compresses each member node’s data with a fixed compression ratio a.
3.2. Radio Model
3.3. Problem Statement
4. Theoretical Analyses
4.1. Energy Neutrality Constrains
4.2. Balancing the Average Energy Consumption of Nodes in Different Units
4.3. Maximizing Network Information Gathering
5. The Detail of Our Protocol


5.1. Clusters Formation
5.2. Routing Heads Selection
6. Performance Evaluations
| Routing Protocol | Routing Category | Harvested Energy Attribute | Network Attribute | Is Perpetual Network Operation Achieved |
|---|---|---|---|---|
| [26] | Flat | Supplement | Single-hop | Not achieved |
| DEHAR | Flat | Only source | Multi-hop | Achieved |
| ENR | Flat | Only source | Single-hop | Achieved |
| [29] | Clustering | Supplement | Single-hop | Not achieved |
| AEHAC | Clustering | Only source | Single-hop | Not achieved |
| EP-LEACH | Clustering | Only source | Single-hop | Not achieved |
| ENC | Clustering | Only source | Single-hop | Achieved |
| MENC | Clustering | Only source | Multi-hop | Achieved |
6.1. Parameters Setup
| Parameters | Values |
|---|---|
| Packet size q (bits) | 1000 |
| Eelec (nJ/bit) | 50 |
| ETx (nJ/bit) | 50 |
| ERx (nJ/bit) | 50 |
| εfs (pJ/bit/m2) | 10 |
| EDA (nJ/bit/message) | 5 |
| Node density ρ (node/100m2) | 1 |
| Compression ratio a | 0.2 |
| Energy harvesting rate Pe (J/h) | 0.5 |
6.2. Simulation Results






7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Akyildiz, I.F.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. Wireless sensor networks: A survey. Comput. Netw. 2002, 38, 393–422. [Google Scholar] [CrossRef]
- Baronti, P.; Pillai, P.; Chook, V.W.C.; Chessa, S.; Gotta, A.; Hu, Y.F. Wireless sensor networks: A survey on the state of the art and the 802.15.4 and zigbee standards. Comput. Commun. 2007, 30, 1655–1695. [Google Scholar] [CrossRef]
- Xu, G.; Shen, W.; Wang, X. Applications of wireless sensor networks in marine environment monitoring: A survey. Sensors 2014, 14, 16932–16954. [Google Scholar] [CrossRef] [PubMed]
- Pino-Povedano, S.; Arroyo-Valles, R.; Cid-Sueiro, J. Selective forwarding for energy-efficient target tracking in sensor networks. Signal Process. 2014, 94, 557–569. [Google Scholar] [CrossRef]
- Cai, X.; Hu, A.; Liu, R. Design of intelligent inductive security system based on wireless sensor network. Energ. Procedia 2011, 12, 718–725. [Google Scholar] [CrossRef]
- Pogkas, N.; Karastergios, G.E.; Antonopoulos, C.P.; Koubias, S.; Papadopoulos, G. Architecture design and implementation of an ad-hoc network for disaster relief operations. IEEE Trans. Ind. Inform. 2007, 3, 63–72. [Google Scholar] [CrossRef]
- Bhende, M.; Wagh, S.J.; Utpat, A. A quick survey on wireless sensor networks. In Proceedings of the 4th International Conference on Communication Systems and Network Technologies (CSNT), Bhopal, India, 7–9 April 2014; pp. 160–167.
- Thalore, R.; Sharma, J.; Khurana, M.; Jha, M.K. Qos evaluation of energy-efficient ML-MAC protocol for wireless sensor networks. AEU Int. J. Electron. Commun. 2013, 67, 1048–1053. [Google Scholar] [CrossRef]
- Lee, J.-H.; Moon, I. Modeling and optimization of energy efficient routing in wireless sensor networks. Appl. Math. Model. 2014, 38, 2280–2289. [Google Scholar] [CrossRef]
- Liu, X. A survey on clustering routing protocols in wireless sensor networks. Sensors 2012, 12, 11113–11153. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Shi, J. Clustering routing algorithms in wireless sensor networks: An overview. KSII Trans. Internet Inf. Syst. 2012, 6, 1735–1755. [Google Scholar] [CrossRef]
- Afsar, M.M.; Tayarani-N, M.-H. Clustering in sensor networks: A literature survey. J. Netw. Comput. Appl. 2014, 46, 198–226. [Google Scholar] [CrossRef]
- Serdaroglu, K.C.; Baydere, S. WiSEGATE: Wireless sensor network gateway framework for internet of things. Wirel. Netw. 2015. [Google Scholar] [CrossRef]
- Collier, S.E. The emerging enernet: Convergence of the smart grid with the internet of things. In Proceedings of the 2015 IEEE Rural Electric Power Conference (REPC), Asheville, NC, USA, 19–21 April 2015; pp. 65–68.
- Abedin, S.F.; Alam, M.G.R.; Rim, H.; Choong Seon, H. A system model for energy efficient green-IoT network. In Proceedings of the 2015 International Conference on Information Networking (ICOIN), Siem Reap, Cambodia, 12–14 January 2015; pp. 177–182.
- Roveda, J.; Lysecky, S.; Young-Jun, S.; Hyungtaek, C.; Annamalai, A.; Xiao, Q. Interface model based cyber-physical energy system design for smart grid. In Proceedings of the 2011 IEEE/IFIP 19th International Conference on VLSI and System-on-Chip (VLSI-SoC), Hong Kong, China, 3–5 October 2011; pp. 368–373.
- Seah, W.G.; Tan, Y.K.; Chan, A.S. Research in Energy Harvesting Wireless Sensor Networks and the Challenges Ahead. In Autonomous Sensor Networks; Filippini, D., Ed.; Springer: Berlin, Germany, 2013; pp. 73–93. [Google Scholar]
- Peng, S.; Low, C.P. Energy neutral routing for energy harvesting wireless sensor networks. In Proceedings of the 2013 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 7–10 April 2013; pp. 2063–2067.
- Valera, A.C.; Soh, W.-S.; Tan, H.-P. Energy-neutral scheduling and forwarding in environmentally-powered wireless sensor networks. Ad Hoc Netw. 2013, 11, 1202–1220. [Google Scholar] [CrossRef]
- Peng, S.; Wang, T.; Low, C.P. Energy neutral clustering for energy harvesting wireless sensors networks. Ad Hoc Netw. 2015, 28, 1–16. [Google Scholar] [CrossRef]
- Yanbing, L.; Yu, M.; Jun, H. Gemini: A green deployment scheme for internet of things. In Proceedings of the 2013 22nd Wireless and Optical Communication Conference (WOCC), Chongqing, China, 16–18 May 2013; pp. 338–343.
- Dehwah, A.H.; Ben Taieb, S.; Shamma, J.S.; Claudel, C.G. Decentralized energy and power estimation in solar-powered wireless sensor networks. In Proceedings of the 2015 International Conference on Distributed Computing in Sensor Systems (DCOSS), Fortaleza, Brazil, 10–12 June 2015; pp. 199–200.
- Li, K.; Yuen, C.; Jha, S. Poster: Fair scheduling for energy harvesting WSN in smart city. In Proceedings of the 13th ACM Conference on Embedded Networked Sensor Systems, Seoul, South Korea, 1–4 November 2015; pp. 419–420.
- Escolar, S.; Chessa, S.; Carretero, J. Energy-neutral networked wireless sensors. Simul. Model. Pract. Theor. 2014, 43, 1–15. [Google Scholar] [CrossRef]
- Meng, J.; Zhang, X.D.; Dong, Y.H.; Lin, X.K. Adaptive energy-harvesting aware clustering routing protocol for wireless sensor networks. In Proceedings of the 2012 7th International ICST Conference on Communications and Networking in China (CHINACOM), Kunming, China, 8–10 August 2012; pp. 742–747.
- Voigt, T.; Ritter, H.; Schiller, J. Solar-aware routing in wireless sensor networks. Lect. Notes Comput. Sci. 2003, 2775, 847–852. [Google Scholar]
- Peng, S.; Low, C.P. Prediction free energy neutral power management for energy harvesting wireless sensor nodes. Ad Hoc Netw. 2014, 13, 351–367. [Google Scholar] [CrossRef]
- Jakobsen, M.K.; Madsen, J.; Hansen, M.R. DEHAR: A distributed energy harvesting aware routing algorithm for ad-hoc multi-hop wireless sensor networks. In Proceedings of the 2010 IEEE International Symposium on A World of Wireless, Mobile and Multimedia Networks (WoWMoM), Montreal, QC, Canada, 14–17 June 2010; pp. 1–9.
- Zhang, P.F.; Xiao, G.X.; Tan, H.P. Clustering algorithms for maximizing the lifetime of wireless sensor networks with energy-harvesting sensors. Comput. Netw. 2013, 57, 2689–2704. [Google Scholar] [CrossRef]
- Xiao, M.; Zhang, X.D.; Dong, Y.H. An effective routing protocol for energy harvesting wireless sensor networks. In Proceedings of the 2013 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 7–10 April 2013; pp. 2080–2084.
- Chen, G.; Li, C.; Ye, M.; Wu, J. An unequal cluster-based routing protocol in wireless sensor networks. Wirel. Netw. 2007, 15, 193–207. [Google Scholar] [CrossRef]
- Heinzelman, W.R.; Chandrakasan, A.; Balakrishnan, H. Energy-Efficient Communication Protocol for Wireless Microsensor Networks. In Proceedings of the 33rd Annual Hawaii International Conference on System Sciences, Maui, HI, USA, 4–7 January 2000; pp. 1–10.
- Younis, O.; Fahmy, S. HEED: A hybrid, energy-efficient, distributed clustering approach for ad hoc sensor networks. IEEE Trans. Mob. Comput. 2004, 3, 366–379. [Google Scholar] [CrossRef]
- Liu, A.-F.; Wu, X.-Y.; Chen, Z.-G.; Gui, W.-H. Research on the energy hole problem based on unequal cluster-radius for wireless sensor networks. Comput. Commun. 2010, 33, 302–321. [Google Scholar] [CrossRef]
- Liu, T.; Li, Q.; Liang, P. An energy-balancing clustering approach for gradient-based routing in wireless sensor networks. Comput. Commun. 2012, 35, 2150–2161. [Google Scholar] [CrossRef]
- Li, H.; Liu, Y.; Chen, W.; Jia, W.; Li, B.; Xiong, J. COCA: Constructing optimal clustering architecture to maximize sensor network lifetime. Comput. Commun. 2013, 36, 256–268. [Google Scholar] [CrossRef]
- Jin, R.-C.; Gao, T.; Song, J.-Y.; Zou, J.-Y.; Wang, L.-D. Passive cluster-based multipath routing protocol for wireless sensor networks. Wirel. Netw. 2013, 19, 1851–1866. [Google Scholar] [CrossRef]
- Liao, Y.; Qi, H.; Li, W.Q. Load-balanced clustering algorithm with distributed self-organization for wireless sensor networks. IEEE Sens. J. 2013, 13, 1498–1506. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Lin, J.-S. Energy efficiency analysis of a chain-based scheme via intra-grid for wireless sensor networks. Comput. Commun. 2012, 35, 507–516. [Google Scholar] [CrossRef]
- Rappaport, T.S. Wireless Communications: Principles and Practice, 1st ed.; IEEE Press: Piscataway, NJ, USA, 1996; pp. 69–138. [Google Scholar]
- Heinzelman, W.B.; Chandrakasan, A.P.; Balakrishnan, H. An application-specific protocol architecture for wireless microsensor networks. IEEE Trans. Wirel. Commun. 2002, 1, 660–670. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Lu, Y.; Zhong, Y.; Wu, X.; Yang, S.X. A Multi-Hop Energy Neutral Clustering Algorithm for Maximizing Network Information Gathering in Energy Harvesting Wireless Sensor Networks. Sensors 2016, 16, 26. https://doi.org/10.3390/s16010026
Yang L, Lu Y, Zhong Y, Wu X, Yang SX. A Multi-Hop Energy Neutral Clustering Algorithm for Maximizing Network Information Gathering in Energy Harvesting Wireless Sensor Networks. Sensors. 2016; 16(1):26. https://doi.org/10.3390/s16010026
Chicago/Turabian StyleYang, Liu, Yinzhi Lu, Yuanchang Zhong, Xuegang Wu, and Simon X. Yang. 2016. "A Multi-Hop Energy Neutral Clustering Algorithm for Maximizing Network Information Gathering in Energy Harvesting Wireless Sensor Networks" Sensors 16, no. 1: 26. https://doi.org/10.3390/s16010026
APA StyleYang, L., Lu, Y., Zhong, Y., Wu, X., & Yang, S. X. (2016). A Multi-Hop Energy Neutral Clustering Algorithm for Maximizing Network Information Gathering in Energy Harvesting Wireless Sensor Networks. Sensors, 16(1), 26. https://doi.org/10.3390/s16010026







