Compressed Symmetric Nested Arrays and Their Application for Direction-of-Arrival Estimation of Near-Field Sources
Abstract
:1. Introduction
2. Data Model and One Existing Method
2.1. Model of DOA Estimation
- (A1)
- The sources are non-Gaussian, and mutually uncorrelated.
- (A2)
- The noise is additive Gaussian one, either white or coloured, and independent of the sources.
- (A3)
- The array is a non-uniform linear array with underlying grid to avoid manifold ambiguity.ss
2.2. Vitual Array Model by Exploiting Fourth Order Cumulants
2.3. The DOA Estimation Method
3. The Proposed Array Geometry and Method
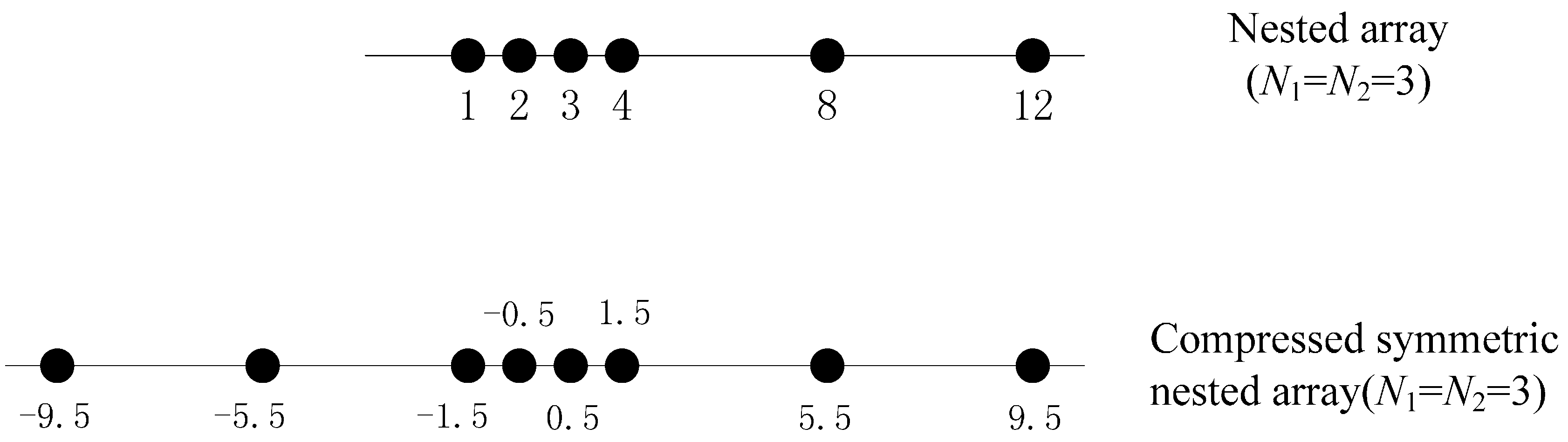
3.1. Nested Array
3.2. Symmetric Nested Array
3.3. Compressed Symmetric Nested Array
3.4. DOA Estimation Using CSNA in the Near-Field
- Use Equation (8) to compute the fourth order cumulants of the observed signals;
- Find from the cumulants;
- Construct matrix using Equation (13);
- Compute the spatial spectrum using Equation (14);
- Find the first peaks of spatial spectrum .
- When SNA is exploited in Equation (12), we can also construct a virtual covariance matrix like Equation (13) and use the conventional MUSIC method to estimate the DOAs. A subspace-based DOA estimation method using a SNA with elements can detect sources. It is obvious that the method based on SNA can identify more sources than sensors when and .
- Since only one half of the difference co-array is employed in our method, the proposed method can detect sources with elements. Compared with the SNA, fewer sensors are acquired for CSNA to detect the same number of sources.
- Regarding the computational complexity of the proposed method, the main cost is in calculating cumulants and eigenvalue decomposition (EVD) of matrix . Calculation of cumulants and EVD of matrix requires and , respectively. When different array geometry is utilized, the dimension of matrix is also different. Without loss of generality, we assume the number of sensors , where is an integer. The value of is presented in Table 2 for ULA, SNA and CSNA respectively.
4. Simulation Results
4.1. Underdetermined DOA Estimation
4.2. Computational Cost
4.3. RMSE versus SNR
4.4. Resolution Ability versus SNR and the Number of Snapshots
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Paulraj, A.; Kailath, T. Esprit—A subspace rotation approach to estimation of parameters of cisoids in noise. IEEE Trans. Acoust. Speech Signal Process. 1986, 34, 1340–1342. [Google Scholar] [CrossRef]
- Huang, Y.-D.; Barkat, M. Near-field multiple source localization by passive sensor array. IEEE Trans. Antennas Propag. 1991, 39, 968–975. [Google Scholar] [CrossRef]
- Chen, J.C.; Hudson, R.E.; Yao, K. Maximum-likelihood source localization and unknown sensor location estimation for wideband signals in the near-field. IEEE Trans. Signal Process. 2002, 50, 1843–1854. [Google Scholar] [CrossRef]
- Grosicki, E.; Abed-Meraim, K.; Hua, Y. A weighted linear prediction method for near-field source localization. IEEE Trans. Signal Process. 2005, 53, 3651–3660. [Google Scholar] [CrossRef]
- Challa, R.N.; Shamsunder, S. High-order subspace-based algorithms for passive localization of near-field sources. In Proceedings of the Twenty-Ninth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 30 October–2 November 1995; pp. 777–781.
- Yuen, N.; Friedlander, B. Performance analysis of higher order esprit for localization of near-field sources. IEEE Trans. Signal Process. 1998, 46, 709–719. [Google Scholar] [CrossRef]
- Liang, J.; Liu, D. Passive localization of near-field sources using cumulant. IEEE Sens. J. 2009, 9, 953–960. [Google Scholar] [CrossRef]
- Liang, J.; Liu, D. Passive localization of mixed near-field and far-field sources using two-stage music algorithm. IEEE Trans. Signal Process. 2010, 58, 108–120. [Google Scholar] [CrossRef]
- Xie, J.; Tao, H.; Rao, X.; Su, J. Passive localization of mixed far-field and near-field sources without estimating the number of sources. Sensors 2015, 15, 3834–3853. [Google Scholar] [CrossRef] [PubMed]
- Hu, K.; Chepuri, S.P.; Leus, G. Near-field source localization using sparse recovery techniques. In Proceedings of the International Conference on Signal Processing and Communications (SPCOM), Bangalore, India, 22–25 July 2014; pp. 1–5.
- Hu, K.; Chepuri, S.P.; Leus, G. Near-field source localization: Sparse recovery techniques and grid matching. In Proceedings of the IEEE 8th Sensor Array and Multichannel Signal Processing Workshop (SAM), A Coruña, Spain, 22–25 June 2014; pp. 369–372.
- Zhang, Y.D.; Qin, S.; Amin, M.G. Near-field source localization based on sparse reconstruction of sensor-angle distribution. In Proceedings of the IEEE International Radar Conference, Arlington, VA, USA, 10–15 May 2015.
- Pillai, S.U.; Bar-Ness, Y.; Haber, F. A new approach to array geometry for improved spatial spectrum estimation. Proc. IEEE 1985, 73, 1522–1524. [Google Scholar] [CrossRef]
- Chevalier, P.; Ferréol, A.; Albera, L. High-resolution direction finding from higher order statistics: The 2q-music algorithm. IEEE Trans. Signal Process. 2006, 54, 2986–2997. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P. Nested arrays: A novel approach to array processing with enhanced degrees of freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef]
- Dogan, M.C.; Mendel, J.M. Applications of cumulants to array processing. I. Aperture extension and array calibration. IEEE Trans. Signal Process. 1995, 43, 1200–1216. [Google Scholar] [CrossRef]
- Ma, W.K.; Hsieh, T.H.; Chi, C.Y. Doa estimation of quasi-stationary signals with less sensors than sources and unknown spatial noise covariance: A khatri–rao subspace approach. IEEE Trans. Signal Process. 2010, 58, 2168–2180. [Google Scholar] [CrossRef]
- Cao, M.-Y.; Huang, L.; Qian, C.; Xue, J.-Y.; So, H.-C. Underdetermined doa estimation of quasi-stationary signals via khatri–rao structure for uniform circular array. Signal Process. 2015, 106, 41–48. [Google Scholar] [CrossRef]
- He, Z.-Q.; Shi, Z.-P.; Huang, L.; So, H.C. Underdetermined doa estimation for wideband signals using robust sparse covariance fitting. IEEE Signal Process. Lett. 2015, 22, 435–439. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P. Multiple level nested array: An efficient geometry for 2qth order cumulant based array processing. IEEE Trans. Signal Process. 2011, 60, 1253–1269. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P.; Pal, P. Sparse sensing with co-prime samplers and arrays. IEEE Trans. Signal Process. 2011, 59, 573–586. [Google Scholar] [CrossRef]
- Liu, C.-L.; Vaidyanathan, P. Super nested arrays: Linear sparse arrays with reduced mutual coupling-part I: Fundamentals. IEEE Trans. Signal Process. 2016, 64, 3997–4012. [Google Scholar] [CrossRef]





| The Number of Sensors ( is an Integer) | The Number of Sensors of Inner ULA | The Number of Sensors of the Outer ULA | The DOF Achieved |
|---|---|---|---|
| ss | |||
| Array Geometry | |
| ULA | |
| SNA | |
| CSNA |
| Methods | Time Consumptions (s) |
|---|---|
| ULA | 0.2719 |
| S-Nested array | 0.2687 |
| CS-Nested array | 0.2743 |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Xie, D. Compressed Symmetric Nested Arrays and Their Application for Direction-of-Arrival Estimation of Near-Field Sources. Sensors 2016, 16, 1939. https://doi.org/10.3390/s16111939
Li S, Xie D. Compressed Symmetric Nested Arrays and Their Application for Direction-of-Arrival Estimation of Near-Field Sources. Sensors. 2016; 16(11):1939. https://doi.org/10.3390/s16111939
Chicago/Turabian StyleLi, Shuang, and Dongfeng Xie. 2016. "Compressed Symmetric Nested Arrays and Their Application for Direction-of-Arrival Estimation of Near-Field Sources" Sensors 16, no. 11: 1939. https://doi.org/10.3390/s16111939
APA StyleLi, S., & Xie, D. (2016). Compressed Symmetric Nested Arrays and Their Application for Direction-of-Arrival Estimation of Near-Field Sources. Sensors, 16(11), 1939. https://doi.org/10.3390/s16111939






