On Performance Analysis of Protective Jamming Schemes in Wireless Sensor Networks
Abstract
:1. Introduction
- In particular, we propose a general theoretical model to quantify the eavesdropping risk (measured by the eavesdropping probability) and evaluate the impact of Fri-Jam schemes on the legitimate communications (measured by the transmission probability).
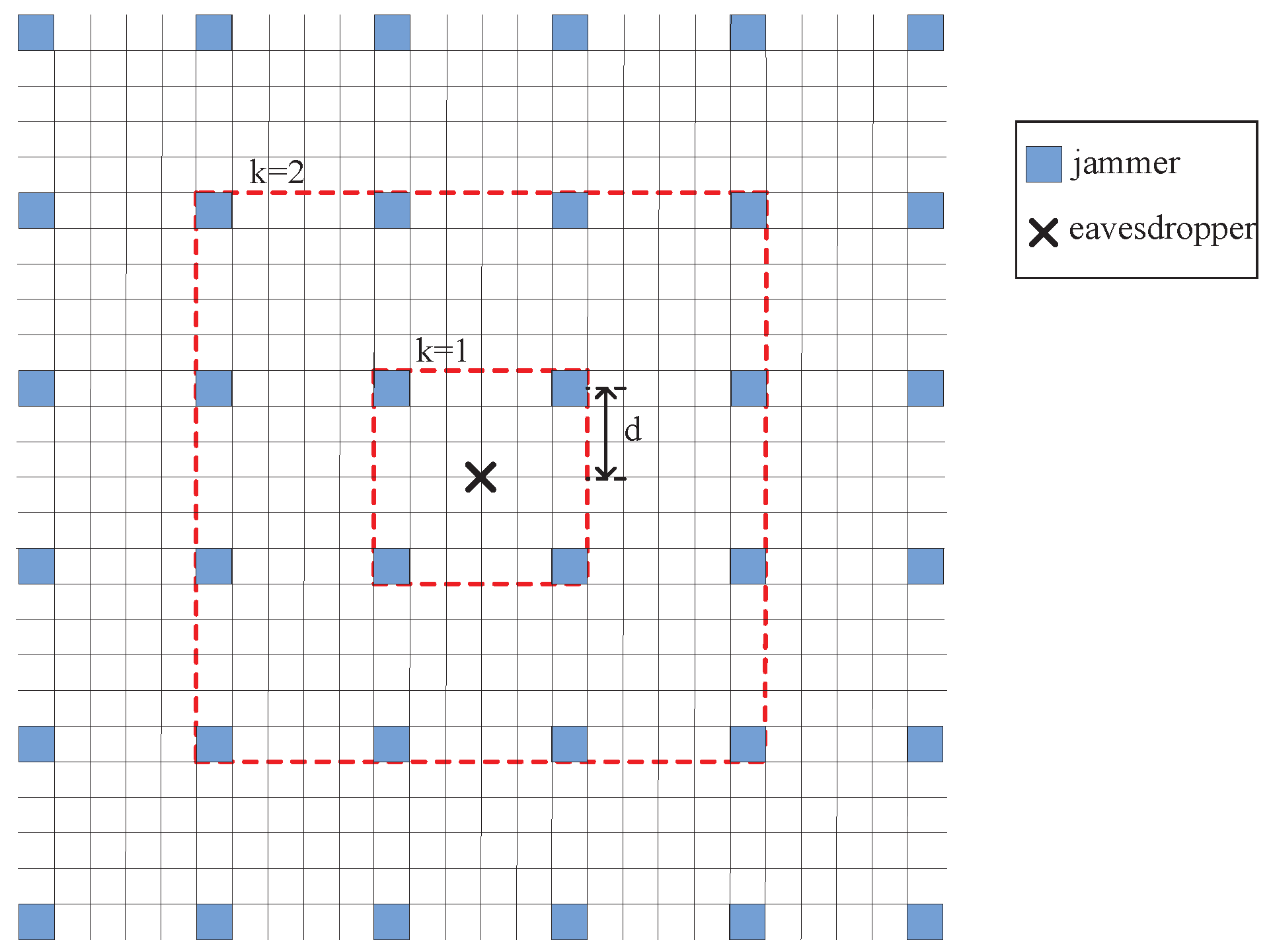
- We consider three types of Fri-Jam schemes: random placement of jammers (named FJ-Ran scheme), regular placement of jammers (named FJ-Reg scheme) and FJ-Reg scheme with power control (named FJ-PC scheme).
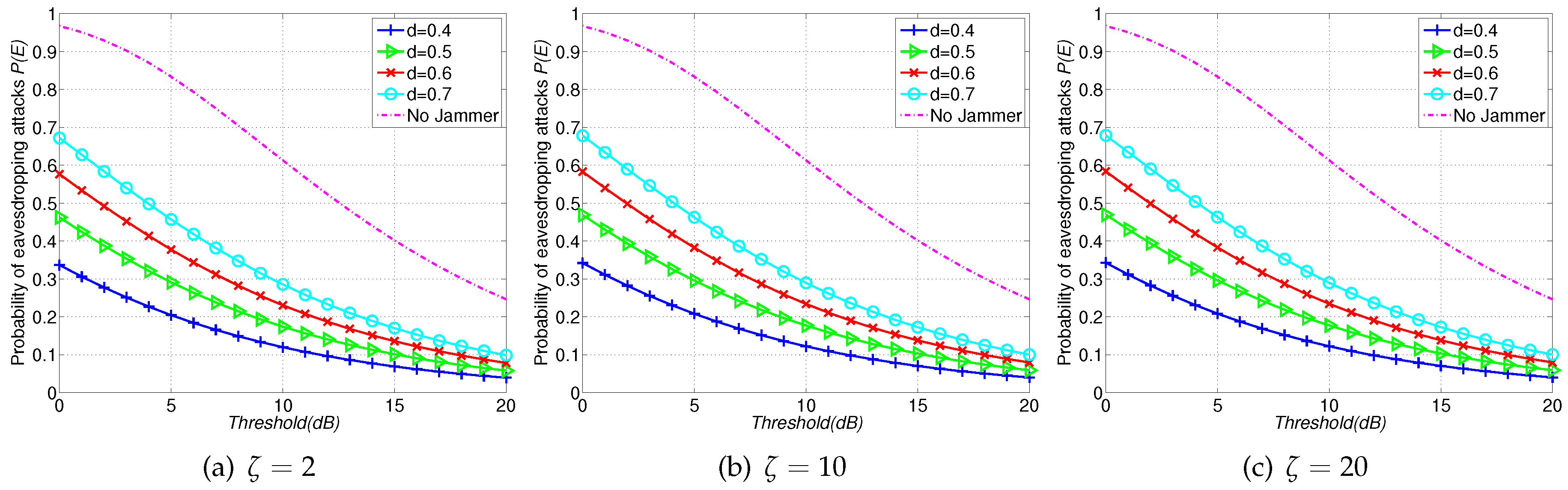
- We compare the eavesdropping probability of WSNs without jammers with that with friendly jammers (FJ-Ran, FJ-Reg and FJ-PC schemes). We find that all of three Fri-Jam schemes can effectively reduce the eavesdropping probability in contrast to no-jamming scenarios.
- Our results also show that the appropriate placement of friendly jammers in WSNs can significantly reduce the eavesdropping probability whilst there is no significant impairment on legitimate communications. Besides, to adjust emitting power of jammers properly can mitigate the eavesdropping risk while has no significant impairment to the legitimate transmission.
2. Related Work
3. System Models
3.1. Fri-Jam Schemes
3.2. Channel Model
3.3. Problem Definition
4. Analysis on Eavesdropping Probability
4.1. Analysis of Non-Jam Scheme
4.2. Analysis of Fri-Jam Schemes
4.2.1. Case I: FJ-Reg Scheme
4.2.2. Case II: FJ-Ran Scheme
4.2.3. Case III: FJ-PC Scheme
5. Numerical Results
5.1. Comparisons of Different Schemes
5.2. Impacts of Friendly Jammers on Legitimate Transmissions
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix B
References
- Lee, E.A. The past, present and future of cyber-physical systems: A focus on models. Sensors 2015, 15, 4837–4869. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Marshall, J.; Wang, D.; Dong, M. Towards Reliable Social Sensing in Cyber-Physical-Social Systems. In Proceedings of the 2016 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), Chicago, IL, USA, 23–27 May 2016.
- Dong, M.; Ota, K.; Liu, A. RMER: Reliable and Energy-Efficient Data Collection for Large-Scale Wireless Sensor Networks. IEEE Int. Things J. 2016, 3, 511–519. [Google Scholar] [CrossRef]
- Tang, Z.; Liu, A.; Huang, C. Social-Aware Data Collection Scheme Through Opportunistic Communication in Vehicular Mobile Networks. IEEE Access 2016, 4, 6480–6502. [Google Scholar] [CrossRef]
- Hu, Y.; Dong, M.; Ota, K.; Liu, A.; Guo, M. Mobile Target Detection in Wireless Sensor Networks with Adjustable Sensing Frequency. IEEE Syst. J. 2016, 10, 1160–1171. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, A. An unequal redundancy level-based mechanism for reliable data collection in wireless sensor networks. EURASIP J. Wirel. Commun. Netw. 2016, 2016, 258. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, M.; Ota, K.; Liu, A. ActiveTrust: Secure and Trustable Routing in Wireless Sensor Networks. IEEE Trans. Inf. Forensics Secur. 2016, 11, 2013–2027. [Google Scholar] [CrossRef]
- Wagner, D.; Schneier, B.; Kelsey, J. Cryptanalysis of the cellular message encryption algorithm. In Advances in Cryptology–CRYPTO ’97; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- 3GPP. General Report on the Design, Speification and Evaluation of 3GPP Standard Confidentiality and Integrity Algorithms; Technical Report; 3GPP: Valbonne, France, 2009. [Google Scholar]
- IEEE Standards Association. 802.11a-1999—IEEE Standard for Telecommunications and Information Exchange Between Systems— LAN/MAN Specific Requirements—Part 11: Wireless Medium Access Control (MAC) and Physical Layer (PHY) Specifications: High Speed Physical Layer in the 5 GHz Band; Technical Report; IEEE: Piscataway, NJ, USA, 1999. [Google Scholar]
- IEEE Standards Association. 802.11i-2004—IEEE Standard for Tnformation Technology—Telecommunications and Information Exchange Between Systems— Local and Metropolitan Area Networks-Specific Requirements—Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications: Amendment 6: Medium Access Control (MAC) Security Enhancements; Technical Report; IEEE: Piscataway, NJ, USA, 2004. [Google Scholar]
- Shim, K.A. A Survey of Public-Key Cryptographic Primitives in Wireless Sensor Networks. IEEE Commun. Surv. Tutorials 2016, 18, 577–601. [Google Scholar] [CrossRef]
- Han, Z.; Marina, N.; Debbah, M.; Hjørungnes, A. Physical Layer Security Game: Interaction Between Source, Eavesdropper, and Friendly Jammer. EURASIP J. Wirel. Commun. Netw. 2009, 2009. [Google Scholar] [CrossRef]
- Zhu, Q.; Saad, W.; Han, Z.; Poor, H.; Basar, T. Eavesdropping and jamming in next-generation wireless networks: A game-theoretic approach. In Proceedings of the 2010 Military Communications Conference, Baltimore, MD, USA, 7–10 November 2011.
- Vilela, J.P.; Bloch, M.; Barros, J.; McLaughlin, S.W. Wireless Secrecy Regions With Friendly Jamming. IEEE Trans. Inf. Forensics Secur. 2011, 6, 256–266. [Google Scholar] [CrossRef]
- Sankararaman, S.; Abu-Affash, K.; Efrat, A.; Eriksson-Bique, S.D.; Polishchuk, V.; Ramasubramanian, S.; Segal, M. Optimization Schemes for Protective Jamming. In Proceedings of the 13th ACM MobiHoc, Hilton Head Island, SC, USA, 11–14 June 2012.
- Kim, Y.S.; Tague, P.; Lee, H.; Kim, H. A Jamming Approach to Enhance Enterprise Wi-Fi Secrecy Through Spatial Access Control. Wirel. Netw. 2015, 21, 2631–2647. [Google Scholar] [CrossRef]
- IEEE Standards Association. IEEE 802.15.4 Enabling Pervasive Wireless Sensor Networks; Technical Report; IEEE: Piscataway, NJ, USA, 2011. [Google Scholar]
- Lakshmanan, S.; Tsao, C.; Sivakumar, R.; Sundaresan, K. Securing Wireless Data Networks against Eavesdropping using Smart Antennas. In Proceedings of the 28th International Conference on Distributed Computing Systems, Beijing, China, 17–20 June 2008.
- Zou, Y.; Zhu, J.; Wang, X.; Hanzo, L. A Survey on Wireless Security: Technical Challenges, Recent Advances, and Future Trends. Proc. IEEE 2016, 104, 1727–1765. [Google Scholar] [CrossRef]
- Ren, K.; Su, H.; Wang, Q. Secret key generation exploiting channel characteristics in wireless communications. IEEE Wirel. Commun. 2011, 18, 6–12. [Google Scholar] [CrossRef]
- Zafer, M.; Agrawal, D.; Srivatsa, M. Limitations of Generating a Secret Key Using Wireless Fading Under Active Adversary. IEEE/ACM Trans. Netw. 2012, 20, 1440–1451. [Google Scholar] [CrossRef]
- Zeng, K. Physical layer key generation in wireless networks: Challenges and opportunities. IEEE Commun. Mag. 2015, 53, 33–39. [Google Scholar] [CrossRef]
- Edman, M.; Kiayias, A.; Tang, Q.; Yener, B. On the Security of Key Extraction From Measuring Physical Quantities. IEEE Trans. Inf. Forensics Secur. 2016, 11, 1796–1806. [Google Scholar] [CrossRef]
- Savry, O.; Pebay-Peyroula, F.; Dehmas, F.; Robert, G.; Reverdy, J. RFID Noisy Reader How to Prevent from Eavesdropping on the Communication? In Proceedings of the 2007 Cryptographic Hardware and Embedded Systems, Vienna, Austria, 10–13 September 2007; pp. 334–345.
- Mukherjee, A.; Fakoorian, S.A.A.; Huang, J.; Swindlehurst, A.L. Principles of physical layer security in multiuser wireless networks: A survey. IEEE Commun. Surv. Tutorials 2014, 16, 1550–1573. [Google Scholar] [CrossRef]
- Hassanieh, H.; Wang, J.; Katabi, D.; Kohno, T. Securing RFIDs by Randomizing the Modulation and Channel. In Proceedings of the 12th USENIX Symposium on Networked Systems Design and Implementation (NSDI 12), Oakland, CA, USA, 4–6 May 2015.
- Kao, J.C.; Marculescu, R. Minimizing Eavesdropping Risk by Transmission Power Control in Multihop Wireless Networks. IEEE Trans. Comput. 2007, 56, 1009–1023. [Google Scholar] [CrossRef]
- Bashar, S.; Ding, Z. Optimum Power Allocation against Information Leakage in Wireless Network. In Proceedings of the 2009 Global Telecommunications Conference, Honolulu, HI, USA, 1–4 December 2009; pp. 1–6.
- Gamal, A.E.; Mammen, J.; Prabhakar, B.; Shah, D. Optimal throughput-delay scaling in wireless networks-part I: The fluid model. IEEE Trans. Inf. Theory 2006, 52, 2568–2592. [Google Scholar] [CrossRef]
- Andrews, J.G.; Baccelli, F.; Ganti, R.K. A Tractable Approach to Coverage and Rate in Cellular Networks. IEEE Trans. Commun. 2011, 59, 3122–3134. [Google Scholar] [CrossRef]
- Min, G.; Wu, Y.; Al-Dubai, A.Y. Performance Modelling and Analysis of Cognitive Mesh Networks. IEEE Trans. Commun. 2012, 60, 1474–1478. [Google Scholar]
- Wu, Y.; Min, G.; Al-Dubai, A.Y. A New Analytical Model for Multi-Hop Cognitive Radio Networks. IEEE Trans. Wirel. Commun. 2012, 11, 1643–1648. [Google Scholar] [CrossRef]
- Wu, Y.; Min, G.; Yang, L.T. Performance Analysis of Hybrid Wireless Networks Under Bursty and Correlated Traffic. IEEE Trans. Veh. Technol. 2013, 62, 449–454. [Google Scholar] [CrossRef]



| Encryption | Artificial Noise | Power Control | |
|---|---|---|---|
| References | [8,9,10,11,18,21,22,23,24] | [25,26,27] | [28] |
| Limitations | computational intensive and power consuming | too specific (only apply for some specific scenarios) | deteriorate legitimate communications |
| Density | Eavesdropping deviation | Transmission deviation |
|---|---|---|
| 0.2 | 0.1120 | 0.0303 |
| 0.8 | 0.3316 | 0.0718 |
| 1.4 | 0.4470 | 0.0880 |
| 2.0 | 0.5178 | 0.0963 |
| Distance d | Eavesdropping deviation | Transmission deviation |
|---|---|---|
| 0.2 | 0.6650 | 0.1143 |
| 0.4 | 0.5195 | 0.0977 |
| 0.6 | 0.3467 | 0.0742 |
| 0.8 | 0.2054 | 0.0500 |
| Distance d | Eavesdropping deviation | Transmission deviation |
|---|---|---|
| 0.4 | 0.4909 | 0.0594 |
| 0.5 | 0.4358 | 0.0362 |
| 0.6 | 0.3788 | 0.0217 |
| 0.7 | 0.3234 | 0.0132 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Dai, H.-N.; Wang, H.; Xiao, H. On Performance Analysis of Protective Jamming Schemes in Wireless Sensor Networks. Sensors 2016, 16, 1987. https://doi.org/10.3390/s16121987
Li X, Dai H-N, Wang H, Xiao H. On Performance Analysis of Protective Jamming Schemes in Wireless Sensor Networks. Sensors. 2016; 16(12):1987. https://doi.org/10.3390/s16121987
Chicago/Turabian StyleLi, Xuran, Hong-Ning Dai, Hao Wang, and Hong Xiao. 2016. "On Performance Analysis of Protective Jamming Schemes in Wireless Sensor Networks" Sensors 16, no. 12: 1987. https://doi.org/10.3390/s16121987
APA StyleLi, X., Dai, H.-N., Wang, H., & Xiao, H. (2016). On Performance Analysis of Protective Jamming Schemes in Wireless Sensor Networks. Sensors, 16(12), 1987. https://doi.org/10.3390/s16121987








