Vision-Based Leader Vehicle Trajectory Tracking for Multiple Agricultural Vehicles
Abstract
:1. Introduction
- (1)
- To establish an autonomous vehicle as a follower vehicle able to conduct tracking tasks.
- (2)
- To construct a robust and accurate monocular vision system able to estimate the relative position between a leader and a follower.
- (3)
- To develop a control algorithm able to realize accurate leader vehicle trajectory-tracking for multiple agricultural machinery combinations, with a human-driven leader and an autonomous follower.
2. Materials and Methods
2.1. Leader-Follower Relative Position and Camera-Marker Sensing System
2.1.1. Camera Servo System
2.1.2. Marker Detection
2.1.3. Marker Positioning
2.1.4. Offset of Roll Angle between Camera and Marker
2.1.5. Transformation of Coordinates and Relative Positioning of the Marker
2.2. Camera Vision Data Estimation and Smoothing
2.3. Design of Control Law for the Leader Trajectory Tracking of the Follower Vehicle
3. Field Experiments
4. Results
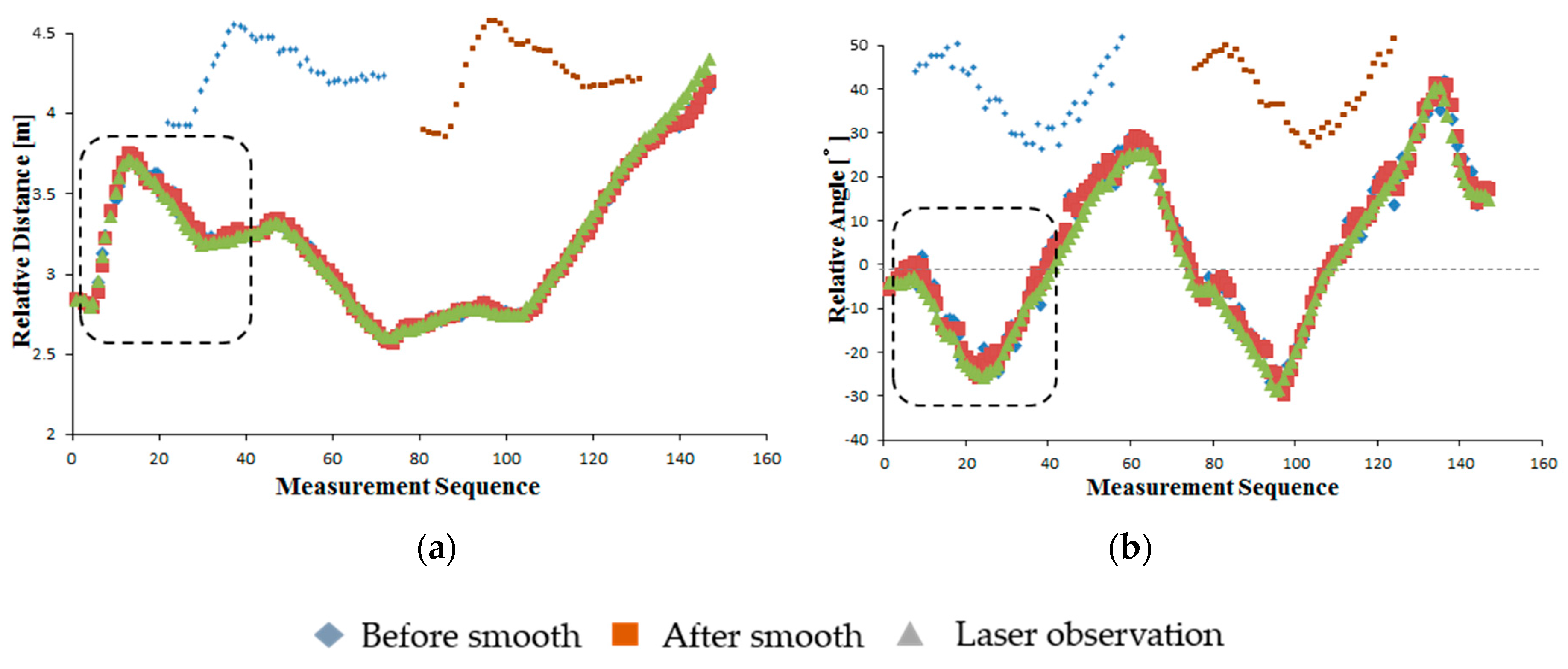
4.1. Evaluation of Camera-Marker Observation System
4.2. Tracking Performance
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclatures
| : Relative distance between the leader and the follower, m | : Vector of fitted current relative distance and relative angle using the stored n points of observation data |
| : Relative heading angle between the leader and the follower | : Vector of the current relative distance and relative angle |
| : Orientation angle of the leader relative to the follower | : Vector of stored observation |
| : Side length of squares on marker, m | : Vector of distance between current observation and last observation |
| : Interval between square centers, m | : Vector of distance between current observation and fitted observation |
| : Angle between square center and camera optical axis | : Vector of threshold values |
| : Angle between optical axis and the follower centerline | : Required position of the follower in the leader-based local coordinates, m |
| : Height of squares in the image plane, m | : Required heading angle of the follower in the leader-based local coordinates |
| : Camera focal length | l: Length of vehicle wheelbase, m |
| : Shift of camera optical axis | : Length from the follower rear wheel axial center to the control point C, m |
| : Roll angle of camera around its optical axis | : Required relative distance between the leader and the follower, m |
| : Coordinate of square centers under image coordinate system, pixel | : Required relative heading angle between the leader and follower |
| : Coordinate of square centers under camera coordinate system, m | : Local position of the control point C in the leader-based local coordinates, m |
| : Coordinates of square centers with respect to the horizontal surface, m | : Local heading of the control point C in the leader-based local coordinates |
| : Coordinates of the square centers in the follower-based local coordinates, m | : Control point C-based lateral tracking error, m |
| , : Local position of the leader based on the follower, m | : Control point C-based longitudinal tracking error, m |
| . : Local heading angle of the leader based on the follower | : Control point C-based heading tracking error |
| : Sequence of stored observation data | : Steering angle of the follower vehicle |
| : Vector of current camera observed data | : Velocity of the follower vehicle, m s−1 |
References
- Iida, M.; Umeda, M.; Suguri, M. Automated follow-up vehicle system for agriculture. J. Jpn. Soc.Agric. Mach. 2001, 61, 99–106. [Google Scholar]
- Noguchi, N.; Barawid, O.J. Robot Farming System Using Multiple Robot Tractors in Japan. Int. Fed. Autom. Control 2011, 18, 633–637. [Google Scholar]
- Johnson, D.A.; Naffin, D.J.; Puhalla, J.S.; Sanchez, J.; Wellington, C.K. Development and Implementation of a Team of Robotic Tractors for Autonomous Peat Moss Harvesting. J. Field Rob. 2009, 26, 549–571. [Google Scholar] [CrossRef]
- Zhang, X.; Geimer, M.; Noack, P.O.; Grandl, L. A semi-autonomous tractor in an intelligent master–slave vehicle system. Intell. Serv. Rob. 2010, 3, 263–269. [Google Scholar] [CrossRef]
- Noguchi, N.; Will, J.; Reid, J.; Zhang, Q. Development of a master–slave robot system for farm operations. Comput. Electron. Agric. 2004, 44, 1–19. [Google Scholar] [CrossRef]
- Morin, P.; Samson, C. Motion Control of Wheeled Mobile Robots. In Springer Handbook of Robotics; Springer: Berlin, Germany, 2008; pp. 799–826. [Google Scholar]
- Ou, M.Y.; Li, S.H.; Wang, C.L. Finite-time tracking control for multiple non-holonomic mobile robots based on visual servoing. Int. J. Control 2013, 12. [Google Scholar] [CrossRef]
- Peng, Z.H.; Wang, D.; Liu, H.T.; Sun, G. Neural adaptive control for leader–follower flocking of networked nonholonomic agents with unknown nonlinear dynamics. Int. J. Adapt Control Signal Process. 2014, 28, 479–495. [Google Scholar] [CrossRef]
- Kise, M.; Noguchi, N.; Ishii, K.; Terao, H. Laser Scanner-Based Obstacle Detection system for Autonomous Tractor -Movement and Shape Detection Targeting at agricultural vehicle. J. Jpn. Soc. Agric. Mach. 2004, 2, 97–104. [Google Scholar]
- Johnson, E.N.; Calise, A.J.; Sattigeri, R.; Watanabe, Y.; Madyastha, V. Approaches to Vision-Based Formation Control. In Proceedings of the 43rd IEEE Conference on Decision and Control, CDC, Nassau, Bahamas, 14–17 December 2004; pp. 1643–1648.
- Goi, H.K.; Giesbrecht, J.L.; Barfoot, T.D.; Francis, B.A. Vision-Based Autonomous Convoying with Constant Time Delay. J. Field Rob. 2010, 27, 430–449. [Google Scholar] [CrossRef]
- Espinosa, F.; Santos, C.; Romera, M.M.; Pizarro, D.; Valdés, F.; Dongil, J. Odometry and Laser Scanner Fusion Based on a Discrete Extended Kalman Filter for Robotic Platooning Guidance. Sensors 2011, 11, 8339–8357. [Google Scholar] [CrossRef] [PubMed]
- Ahamed, T.; Tian, L.; Takigawa, T.; Zhang, Y. Development of Auto-Hitching Navigation System for Farm Implements using Laser Range Finder. Trans. ASABE 2009, 52, 1793–1803. [Google Scholar] [CrossRef]
- Gou, A.; Akira, M.; Noguchi, N. Study on a Straight Follower Control Algorithm based on a Laser Scanner. J. Jpn. Soc.Agric. Mach. 2005, 67, 65–71. [Google Scholar]
- Takigawa, T.; Koike, M.; Honma, T.; Hasegawa, H.; Zhang, Q.; Ahamed, T. Navigation using a Laser Range Finder for Autonomous Tractor (Part 1)-Positioning of Implement. J. Jpn. Soc. Agric. Mach. 2006, 68, 68–77. [Google Scholar]
- Han, S.; Zhang, Q.; Ni, B.; Reid, J.F. A guidance directrix approach to vision-based vehicle guidance system. Comput. Electron. Agric. 2004, 43, 179–195. [Google Scholar] [CrossRef]
- Courbon, J.; Mezouar, Y.; Guenard, N.; Martinet, P. Vision-based navigation of unmanned aerial vehicles. Control Eng. Pract. 2010, 18, 789–799. [Google Scholar] [CrossRef]
- Caballero, F.; Merino, L.; Ferruz, J.; Ollero, A. Vision-based odometry and SLAM for medium and high altitude flying UAVs. J. Intell. Rob. Syst. Theory Appl. 2009, 54, 137–161. [Google Scholar] [CrossRef]
- Hasegawa, H.; Takigawa, T.; Koike, M.; Yoda, A.; Sakai, N. Studies on Visual Recognition of an Agricultural Autonomous Tractor-Detection of the Field State by Image Processing. Jpn. J. Farm Work Res. 2000, 35, 141–147. [Google Scholar] [CrossRef]
- Kannan, S.K.; Johnson, E.N.; Watanabe, Y.; Sattigeri, R. Vision-Based Tracking of Uncooperative Targets. Int. J.Aerosp. Eng. 2011, 2011. [Google Scholar] [CrossRef]
- Krajnik, T.; Nitsche, M.; Faigl, J.; Vanek, P.; Saska, M.; Preucil, L.; Duckett, T.; Mejail, M. A practical multirobot localization system. J. Intell. Rob. Syst. 2014, 76, 539–562. [Google Scholar] [CrossRef] [Green Version]



















© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Ahamed, T.; Zhang, Y.; Gao, P.; Takigawa, T. Vision-Based Leader Vehicle Trajectory Tracking for Multiple Agricultural Vehicles. Sensors 2016, 16, 578. https://doi.org/10.3390/s16040578
Zhang L, Ahamed T, Zhang Y, Gao P, Takigawa T. Vision-Based Leader Vehicle Trajectory Tracking for Multiple Agricultural Vehicles. Sensors. 2016; 16(4):578. https://doi.org/10.3390/s16040578
Chicago/Turabian StyleZhang, Linhuan, Tofael Ahamed, Yan Zhang, Pengbo Gao, and Tomohiro Takigawa. 2016. "Vision-Based Leader Vehicle Trajectory Tracking for Multiple Agricultural Vehicles" Sensors 16, no. 4: 578. https://doi.org/10.3390/s16040578
APA StyleZhang, L., Ahamed, T., Zhang, Y., Gao, P., & Takigawa, T. (2016). Vision-Based Leader Vehicle Trajectory Tracking for Multiple Agricultural Vehicles. Sensors, 16(4), 578. https://doi.org/10.3390/s16040578





