Damage Detection Based on Power Dissipation Measured with PZT Sensors through the Combination of Electro-Mechanical Impedances and Guided Waves
Abstract
:1. Introduction
2. Electro-Mechanical Power Dissipation as a New Damage Indicator
2.1. Basis of Piezoelectric Sensing for SHM
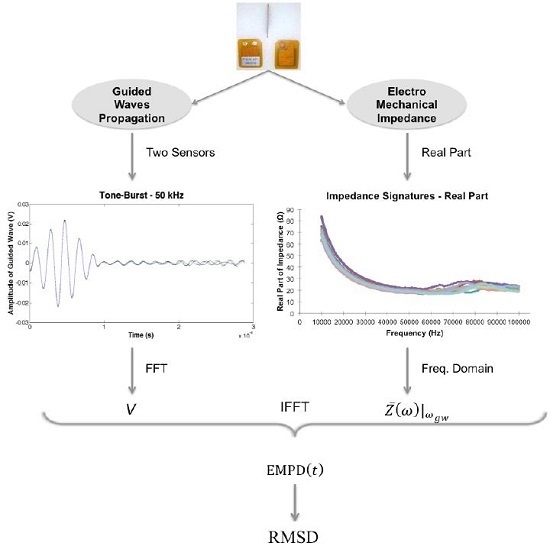
2.2. Definition of Electro-Mechanical Power Dissipation
- The guided waves used in this work are sent and received at a particular frequency, while the impedance signatures are obtained by performing a sweep in the frequency domain. This implies that, after expressing both signals in the frequency domain, the electro-mechanical impedance will show a different amplitude at each frequency. However, after applying the corresponding filter, just one significant non-zero amplitude will be found for the measured voltage in the frequency domain. For this reason, just the corresponding value at this frequency is taken from the electro-mechanical signal.
- As it is not the purpose of this paper to provide a rigorous mathematical explanation about the analogy between the EMPD and the one measured on a real electric circuit, the authors have not considered any phase dependency between the voltage and the current, which has been possible due to the fact that absolute magnitudes have been used in Equations (2) and (3).
2.3. Damage Detection Procedure
- (a)
- Collection of baseline impedance signals and guided waves. In the case of the electro-mechanical impedance, one signature is obtained per PZT sensor embedded in the host structure. In order to enhance the accuracy of the process, several measurements can be taken in order to work in the subsequent stages with the average of all those measurements. Once the impedance signatures are stored, guided waves will be measured, obtaining two different signals between every two sensors: one sent from the first sensor and measured at the second one, and vice versa.
- (b)
- All experimental procedures imply the presence of environmental noise, and given that these sets of measurements are taken at high frequencies, the following step is to clean each signal from undesired noises. The influence of the noise on the electro-mechanical impedance is already minimized thanks to the impedance analyzer used, which employs a measuring technique that calculates the average between a number of neighbouring sample points, but a bandpass filter (which depends on the particular application) is needed for the guided wave signals.
- (c)
- To compute EMPD, the Fast Fourier Transform (FFT) is applied to all guided wave signals in order to obtain their corresponding values in the frequency domain. As each of these signals is sent and measured at a particular frequency, a single point would be expected in the frequency domain. However, there is still some negligible noise present after the filtering process, which is going to reveal some more frequencies after the FFT is applied. The corresponding value of the electro-mechanical impedance at that frequency must be selected, so that the Electro-Mechanical Power can be defined using an extension of Equation (2). As only one impedance signature is available per sensor, the value considered in this case has been the average of the impedances measured at the corresponding two consecutive sensors used to measure each guided wave.
- (d)
- The Inverse Fast Fourier Transform (IFFT) is applied in order to obtain the expression of the EMPD in time domain. The signal obtained in this step will be used as a baseline in the subsequent iteration, so only the appearance of new damage with respect to the baseline stage should be reflected by the damage index.
- (e)
- Repeat steps (a) to (d) for each of the studied damage cases of each experiment, so that the corresponding EMPD signatures can be obtained for each health condition of the structure.
- (f)
- Once the EMPD is obtained for each of the damage scenarios, the following step is to define an appropriate damage indicator that allows the analysis of the health condition of the corresponding structure. The root mean square deviation (RMSD) is the most commonly used indicator to assess damage [20,31,32], and is computed from the difference in the EMPD value at each timepoint aswhere is the EM power dissipation of the PZT measured at a previous stage, which might agree with the healthy condition of the structure; is the corresponding value at a subsequent stage, which might agree with a post-damage stage, at the ith timepoint; n is the number of timepoints. For the RMSD index, the larger the difference between the baseline reading and the subsequent reading, the greater the value of the index denoting changes in structural dynamic properties which can be due to damage.
3. Experimental Study for Lab-Scale Structures
3.1. Bolt Loosening Detection in an Aluminium Lap Joint
3.2. Induced Debonding on an FRP-Strengthened Concrete Specimen
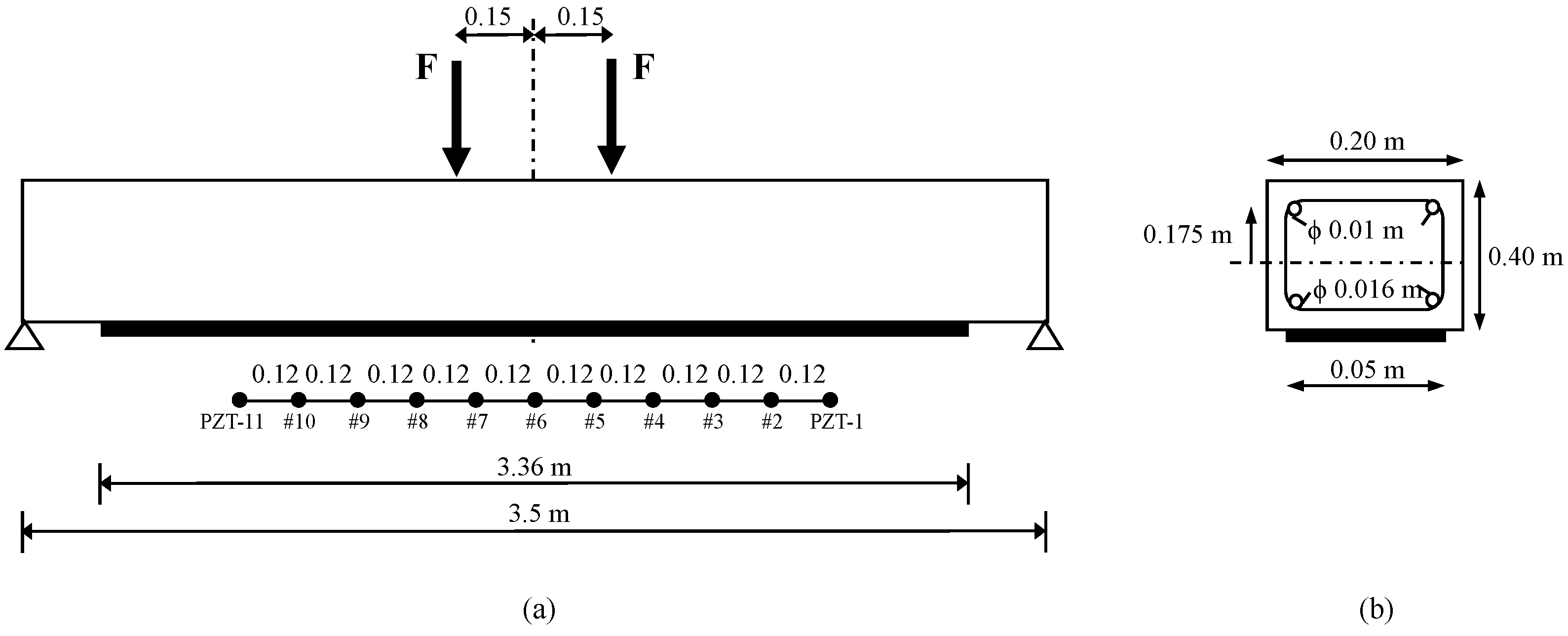
4. Debonding Assessment in a Real-Scale RC Beam Externally Strengthened with FRP
4.1. Test Description
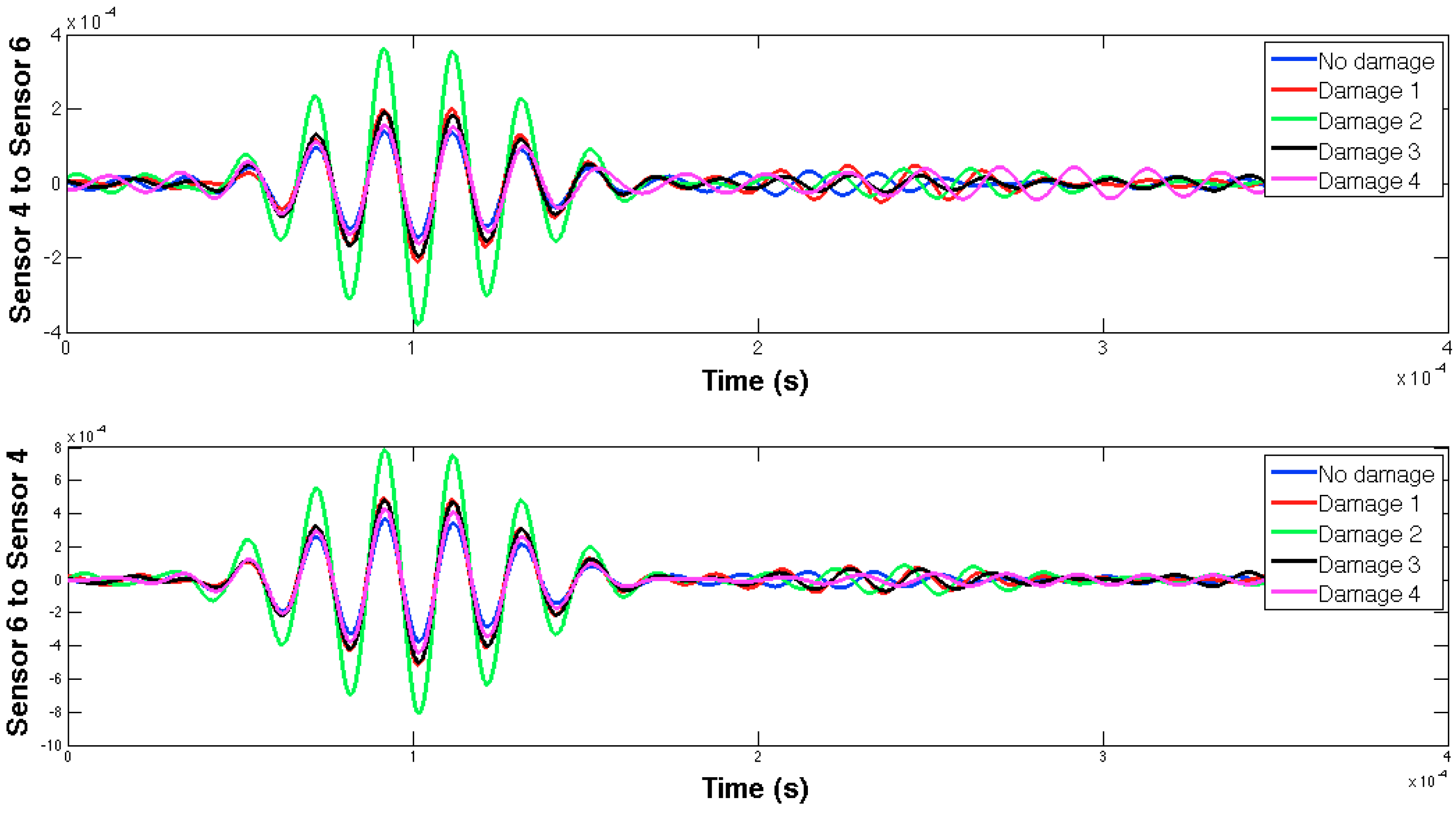
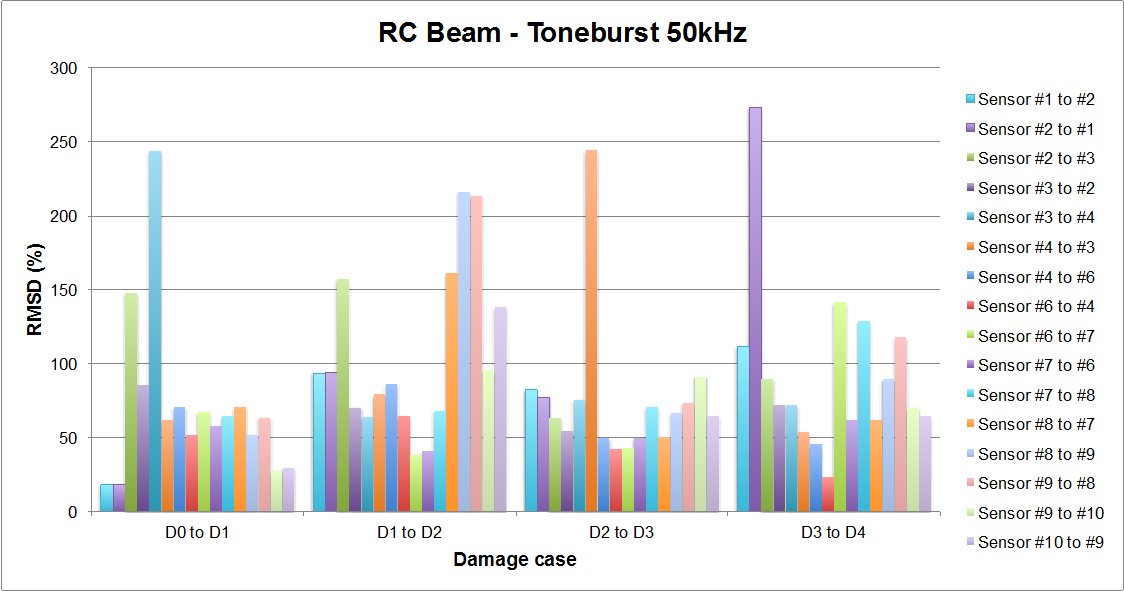
4.2. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| SHM | Structural Health Monitoring |
| NDT | Non-Destructive Testing |
| PZT | Lead-Zirconate-Titanate |
| EMI | Electro-Mechanical Impedance |
| EMPD | Electro-Mechanical Power Dissipation |
| FFT | Fast Fourier Transform |
| IFFT | Inverse Fast Fourier Transform |
References
- Sohn, H.; Farrar, C.R.; Hemez, F.M.; Shunk, D.D.; Stinemates, D.W.; Nadler, B.R.; Czarnecki, J.J. A Review of Structural Health Monitoring Literature: 1996–2001; Los Alamos National Laboratory Report LA-13976-MS; Los Alamos National Labs: Los Alamos, NM, USA, 2004.
- Bhalla, S.; Soh, C.K. High frequency piezoelectric signatures for diagnosis of seismic/blast induced structural damages. NDT&E Int. 2004, 37, 23–33. [Google Scholar]
- Chang, P.C.; Flatau, A.; Liu, S.C. Review Paper: Health Monitoring of Civil Infrastructure. Struct. Health Monit. 2003, 2, 257–267. [Google Scholar] [CrossRef]
- Fang, S.E.; Perera, R.; De Roeck, G. Damage identification of a reinforced concrete frame by finite element model updating using damage parameterization. J. Sound Vibr. 2008, 313, 544–559. [Google Scholar] [CrossRef]
- Perera, R.; Marín, R.; Ruiz, A. Static-dynamic multiscale structural damage identification in a multi-objective framework. J. Sound Vibr. 2013, 332, 1484–1500. [Google Scholar] [CrossRef]
- Chang, P.C.; Liu, S.C. Recent Research in Nondestructive Evaluation of Civil Infrastructures. J. Mater. Civil Eng. 2003, 15, 298–304. [Google Scholar] [CrossRef]
- Leo, D.J. Engineering Analysis of Smart Material Systems; John Wiley & Sons: New Jersey, NJ, USA, 2007. [Google Scholar]
- Laflamme, S.; Cao, L.; Chatzi, E.; Ubertini, F. Damage Detection and Localization from Dense Network of Strain Sensors. Shock Vibr. 2016, 2016, 2562949. [Google Scholar] [CrossRef]
- Teng, J.G.; Chen, J.F.; Smith, S.T.; Lam, L. CFRP Strengthened RC Structures, 1st ed.; John Wiley and Sons: West Sussex, UK, 2002. [Google Scholar]
- Giurgiutiu, V. Structural Health Monitoring with Piezoelectric Wafer Active Sensors, 1st ed.; Elsevier Inc.: San Diego, CA, USA, 2008. [Google Scholar]
- Liang, C.; Sun, F.P.; Rogers, C.A. Coupled electro-mechanical analysis of adaptive material systems determination of the actuator power consumption and system energy transfer. J. Intell. Mater. Syst. Struct. 1994, 5, 12–20. [Google Scholar] [CrossRef]
- Yang, Y.; Divsholli, B.S. Sub-Frequency Interval Approach in Electromechanical Impedance Technique for Concrete Structure Health Monitoring. Sensors 2010, 10, 11644–11661. [Google Scholar] [CrossRef] [PubMed]
- Sevillano, E.; Sun, R.; Gil, A.; Perera, R. Interfacial crack-induced debonding identification in FRP-strengthenined RC beams from PZT signatures using hierarchical clustering analysis. Compos. Part B Eng. 2015, 87, 322–335. [Google Scholar] [CrossRef]
- Min, J.P.S.; Yun, C.B.; Lee, C.G.; Lee, C. Impedance-based structural health monitoring incorporating neural network technique for identification of damage type and severity. Eng. Struct. 2012, 39, 210–220. [Google Scholar] [CrossRef]
- Worlton, D.C. Experimental confirmation of Lamb waves at megacycle frequencies. J. Appl. Phys. 1961, 32, 967–971. [Google Scholar] [CrossRef]
- Raghavan, A. Guided-Wave Structural Health Monitoring. Ph.D Thesis, The University of Michigan, Ann Arbor, MI, USA, 2007. [Google Scholar]
- Providakis, C.P.; Angeli, G.M.; Favvata, M.J.; Papadopoulos, N.A.; Chalioris, C.E.; Karayannis, C.G. Detection of Concrete Reinforcement Damage Using Piezoelectric Materials—Analytical and Experimental Study, World Academy of Science, Engineering and Technology. Int. J. Civil Environ. Struct. Constr. Archit. Eng. 2014, 8, 197–205. [Google Scholar]
- An, Y.K.; Sohn, H. Integrated impedance and guided wave based damage detection. Mech. Syst. Sign. Process. 2012, 28, 50–62. [Google Scholar] [CrossRef]
- Saafi, M.; Sayyah, T. Health monitoring of concrete structures strengthened with advanced composite materials using piezoelectric transducers. Compos. Part B Eng. 2001, 32, 333–342. [Google Scholar] [CrossRef]
- Giurgiutiu, V.; Reynolds, A.; Rogers, C.A. Experimental Investigation of E/M Impedance Health Monitoring for Spot-Welded Structural Joints. J. Intell. Mater. Syst. Struct. 1999, 10, 802–812. [Google Scholar] [CrossRef]
- Giurgiutiu, V.; Harries, K.; Petrou, M.; Bost, J.; Quattlebaum, J.B. Disbond detection with piezoelectriz wafer active sensors in RC structures strengthened with CFRP composite overlays. Earthq. Eng. Vibr. 2003, 2, 213–223. [Google Scholar] [CrossRef]
- Wang, D.S.; Yu, L.P.; Zhu, H.P. Strength monitoring of concrete based on embedded PZT transducer and the resonant frequency. In Proceedings of the Symposium on Piezoelectricity, Acoustic Waves and Device Applications (SPAWDA), Xiamen, China, 10–13 December 2010; pp. 202–205.
- Park, G.; Farrar, C.R.; Rutherford, A.C.; Robertson, A.C. Piezoelectric active sensor self-diagnosis using electric admittance measurements. J. Vibr. Acoust. 2006, 128, 469–476. [Google Scholar] [CrossRef]
- Raghavan, A.C. Review of Guided Wave Structural Health Monitoring. Shock Vibr. Digest 2007, 39, 91–114. [Google Scholar] [CrossRef]
- Viktorov, I.A. Rayleigh and Lamb Waves, 1st ed.; Plenum Press: New York, USA, 1967. [Google Scholar]
- Rose, J.L. Ultrasonic Waves in Solid Media; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Ostachowicz, W.; Kudela, P.; Krawczuk, M.; Zak, A. Guided Waves in Structures for SHM: The Time-Domain Spectral Element Method, 1st ed.; Wiley: West Sussex, UK, 2012. [Google Scholar]
- Alleyne, D.; Cawley, P. The interaction of Lamb waves with defects. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1992, 39, 381–397. [Google Scholar] [CrossRef] [PubMed]
- Cawley, P.; Alleyne, D. The use of Lamb wave for the long range inspection of large structures. Ultrasonics 1996, 34, 287–290. [Google Scholar] [CrossRef]
- Hsu, J.; WP, M.L.; Bascom, S.D. Nanometer distance regulation using electromechanical power dissipation. U.S. Patent No. 5,886,532, 23 March 1999. [Google Scholar]
- Perais, D.M.; Tarazaga, P.A.; Inman, D.J. A study on the correlation between PZT and MFC resonance peaks and adequate damage detection frequency intervals using the impedance method. In Proceedings of the International Conference on Noise & Vibration Engineering (ISMA), Leuven, Belgium, 18–20 September 2006; pp. 18–20.
- Saravanan, T.J.; Balamonica, K.; Priya, C.B.; Gopalakrishnan, N.; Murthy, S.G.N. Non-Destructive Piezo electric based monitoring of strength gain in concrete using smart aggregate. In Proceedings of the International Symposium Non-Destructive Testing in Civil Engineering (NDT-CE), Berlin, Germany, 15–17 September 2015.
- Krishnamurthy, K.; Lalande, F.; Rogers, C.A. Effects of temperature on the electrical impedance of piezoelectric sensors. Proc. SPIE 2717 1996, 2003, 451–463. [Google Scholar]
- Annamdas, V.G.M.; Yang, Y.; Soh, C.K. Influence of loading on the electromechanical admittance of piezoceramic transducers. Smart Mater. Struct. 2007, 16, 1888–1897. [Google Scholar] [CrossRef]
- PI Piezo Technology, P-876 DuraAct Patch Transducer Whitepaper. 2014. Available online: http://piceramic.com/product-detail-page/p-876-101790.html (accessed on 1 February 2014).
- Pesic, N.; Pilakoutas, K. Concrete beams with externally bonded flexural FRP-reinforcement: Analytical investigation of debonding failure. Compos. Part B Eng. 2003, 34, 327–338. [Google Scholar] [CrossRef]
- Liu, S.T.; Oehlers, D.J.; Seracino, R. Study of Intermediate Crack Debonding in Adhesively Plated Beams. J. Compos. Constr. 2007, 11, 175–183. [Google Scholar] [CrossRef]
- Sun, R.; Sevillano, E.; Perera, R. A discrete spectral model for intermediate crack debonding in FRP-strengthened RC beams. Compos. Part B 2015, 69, 562–575. [Google Scholar] [CrossRef]





























© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sevillano, E.; Sun, R.; Perera, R. Damage Detection Based on Power Dissipation Measured with PZT Sensors through the Combination of Electro-Mechanical Impedances and Guided Waves. Sensors 2016, 16, 639. https://doi.org/10.3390/s16050639
Sevillano E, Sun R, Perera R. Damage Detection Based on Power Dissipation Measured with PZT Sensors through the Combination of Electro-Mechanical Impedances and Guided Waves. Sensors. 2016; 16(5):639. https://doi.org/10.3390/s16050639
Chicago/Turabian StyleSevillano, Enrique, Rui Sun, and Ricardo Perera. 2016. "Damage Detection Based on Power Dissipation Measured with PZT Sensors through the Combination of Electro-Mechanical Impedances and Guided Waves" Sensors 16, no. 5: 639. https://doi.org/10.3390/s16050639
APA StyleSevillano, E., Sun, R., & Perera, R. (2016). Damage Detection Based on Power Dissipation Measured with PZT Sensors through the Combination of Electro-Mechanical Impedances and Guided Waves. Sensors, 16(5), 639. https://doi.org/10.3390/s16050639