Detuned Plasmonic Bragg Grating Sensor Based on a Defect Metal-Insulator-Metal Waveguide
Abstract
:1. Introduction
2. Structures and Theoretical Analysis
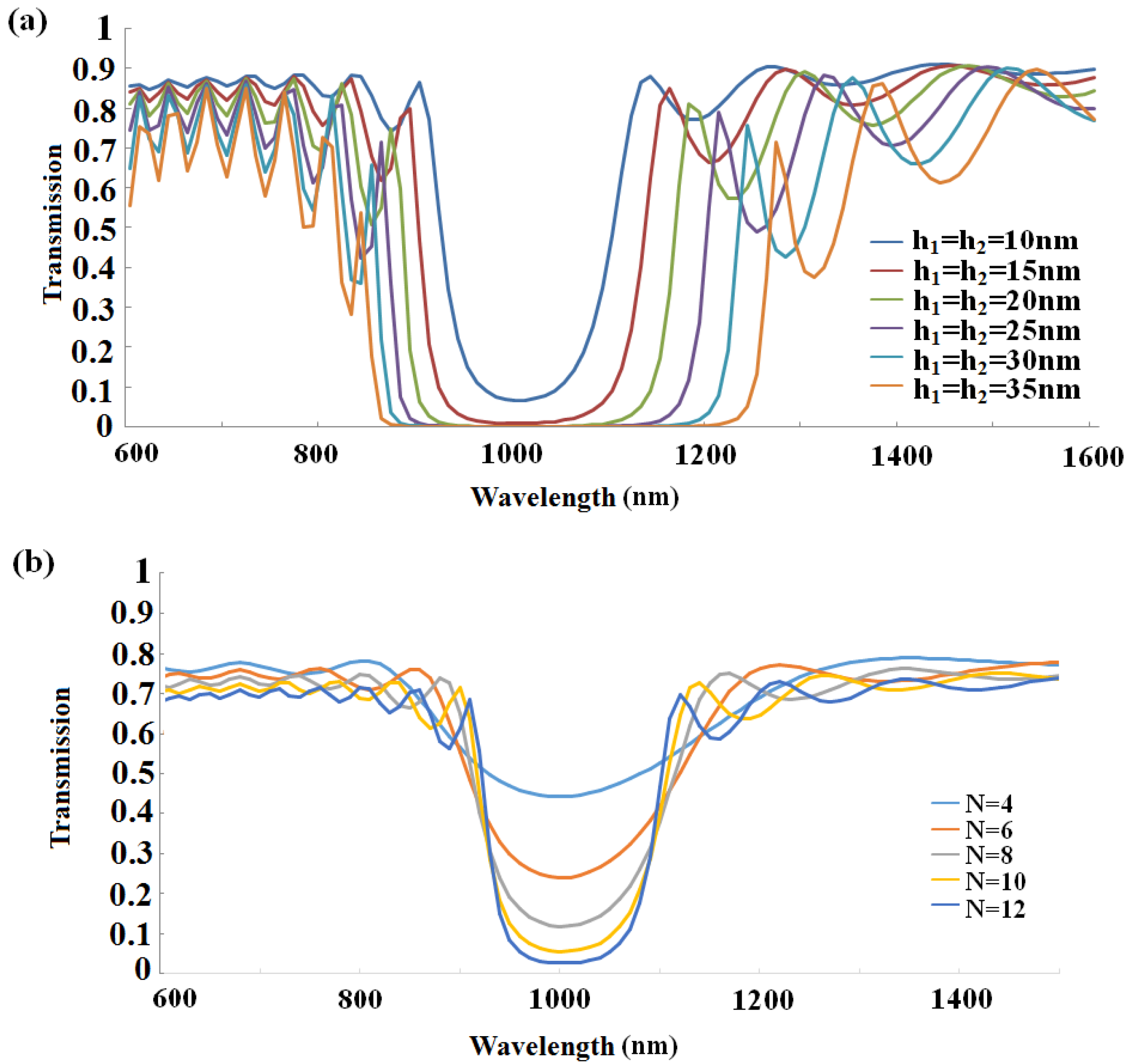
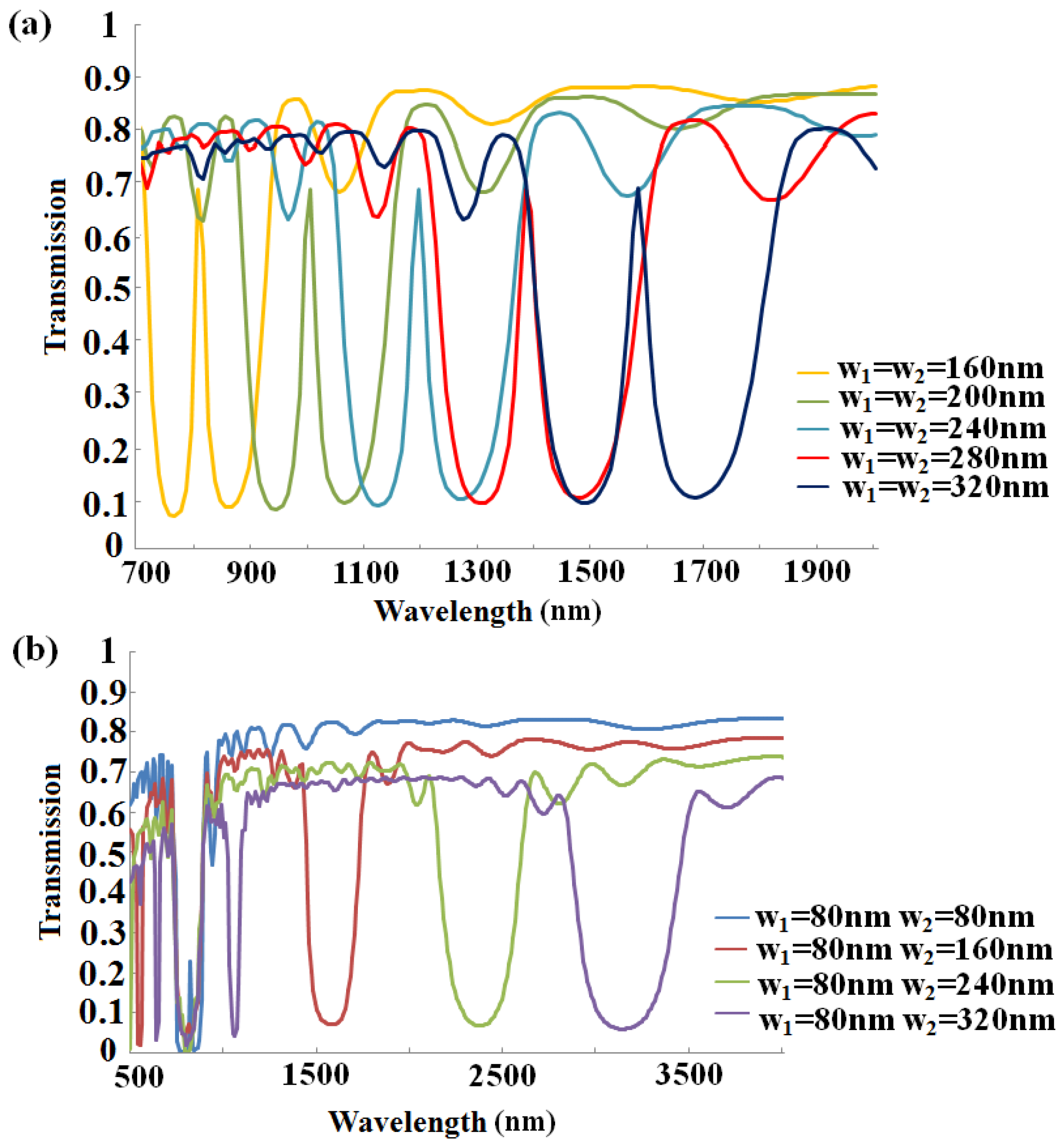
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Han, Z.; Liu, L.; Forsberg, E. Ultra-compact directional couplers and Mach-Zehnder interferometers employing surface plasmon polaritons. Opt. Commun. 2006, 259, 690–695. [Google Scholar] [CrossRef]
- Zia, R.; Selker, D.M.; Catrysse, P.B.; Brongrsma, M.L. Geometries and materials for subwavelength surface plasmon modes. J. Opt. Soc. Am. 2004, 21, 2442–2446. [Google Scholar] [CrossRef]
- Jafarian, B.; Nozhat, N.; Granpayeh, N. Analysis of a triangular-shaped plasmonic metal-insulator-metal Bragg grating waveguide. J. Opt. Soc. Korea 2011, 15, 118–123. [Google Scholar] [CrossRef]
- Min, C.; Veronis, G. Absorption switches in metaldielectric-metal plasmonic waveguides. Opt. Express 2009, 17, 10757–10766. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Kim, H.; Lee, B. High order plasmonic Bragg reflection in the metal-insulator-metal waveguide Bragg grating. Opt. Express 2008, 16, 413–425. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.Q.; Wang, L.L.; He, M.D.; Huang, W.Q.; Wang, D.; Zou, B.S.; Wen, S. A wide bandgap plasmonic Bragg reflector. Opt. Express 2008, 16, 4888–4894. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, A.; Massoud, Y. A low-loss metal-insulatormetal plasmonic Bragg reflector. Opt. Express 2006, 14, 11318–11323. [Google Scholar] [CrossRef]
- Lu, X.Y.; Wan, R.G.; Zhang, T.Y. Metal-dielectric-metal based narrow band absorber for sensing applications. Opt. Express 2015, 23, 29842–29847. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.J. Design and analysis of metal/multi-insulator/metal waveguide plasmonic Bragg grating. Opt. Express 2010, 18, 13258–13270. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Lu, P.; Tian, M.; Liu, D.M.; Zhang, J.S. A subwavelength MIM waveguide filter with single-cavity and multi-cavity structures. Optik 2013, 124, 3701–3704. [Google Scholar] [CrossRef]
- Shin, J.S.; Park, T.H.; Chu, W.S.; Lee, C.H.; Shin, S.Y.; Oh, M.C. Tunable channel-drop filters consisting of polymeric Bragg reflectors and a mode sorting asymmetric X-junction. Opt. Express 2015, 23, 17223–17228. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.F.; Liu, Y.; Kim, J. Characteristics of plasmonic Bragg reflectors with insulator width modulated in sawtooth profiles. Opt. Express 2010, 18, 11589–11598. [Google Scholar] [CrossRef] [PubMed]
- Neutens, P.; Lagae, L.; Borghs, G.; Dorpe, P.V. Plasmon filter and resonator in metal-insulator-metal waveguides. Opt. Express 2012, 20, 3408–3423. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Wang, P.G. Plasmon Bragg reflectors and nanocavities on flat metallic surfaces. Appl. Phys. Lett. 2005, 87, 1–3. [Google Scholar] [CrossRef]
- Chao, C.Y.; Guo, L.J. Design and optimization of microring resonators in biochemical sensing applications. J. Lightwave Technol. 2006, 24, 1395–1402. [Google Scholar] [CrossRef]
- Luff, B.J.; Harris, R.D.; Wilkinson, J.S.; Wilson, R.; Schiffrin, D.J. Integrated-optical directional coupler biosensor. Opt. Lett. 1996, 21, 618–620. [Google Scholar] [CrossRef] [PubMed]
- Zeng, B.; Gao, Y.; Bartoli, J.F. Differentiating surface and bulk interactions in nanoplasmonic interferometric sensor arrays. Nanoscale 2015, 7, 166–170. [Google Scholar] [CrossRef] [PubMed]
- Bahramipanaha, M.; Abrishamiana, M.S.; Mirtaheria, S.A.; Liu, J.M. Ultracompact plasmonic loop-stub notch filter and sensor. Sens. Actuators B Chem. 2014, 194, 311–318. [Google Scholar] [CrossRef]
- Ge, C.W.; Guo, Z.Y.; Sun, Y.X.; Shen, F.; Tao, Y.F.; Zhang, J.R.; Li, R.Z.; Luo, L.B. Spatial and spectral selective characteristics of the plasmonic sensing using metallic nanoslit arrays. Opt. Commun. 2016, 359, 393–398. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Liu, G.Q.; Liu, X.S.; Huang, S.; Pan, P.P.; Wang, Y.; Zou, C.W.; Gu, G. Improving plasmon sensing performance by exploiting the spatially confined field. Plasmonics 2016, 11, 29–36. [Google Scholar] [CrossRef]
- Lee, H.C.; Li, C.T.; Chen, H.F.; Yen, T.J. Demonstration of an ultrasensitive refractive index plasmonic sensor by enabling its quadrupole resonance in phase interrogation. Opt. Lett. 2015, 40, 5152–5155. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.Y.; Gu, J.Q.; Xie, X.C.; Zhang, W.L. Trapping and releasing light by mechanical implementation in metamaterial waveguides. JOSA A 2011, 28, 272–277. [Google Scholar] [CrossRef] [PubMed]
- Xiao, L.; Chen, L.; Li, Y.L.; Liu, J.S.; Wang, K.J. High-speed rainbow trapping and release by mechanical approaches in the terahertz regime. J. Mod. Opt. 2012, 59, 686–692. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Song, Z.M.; Li, Y.F.; Hu, M.L.; Xing, Q.R.; Zhang, Z.G.; Chai, L.; Wang, C.Y. Effective surface plasmon polaritons on the metal wire with arrays of subwavelength grooves. Opt. Express 2006, 14, 13021–13029. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Liu, Y.; Yu, Z.; Peng, Y.; Shu, C.; Ye, H. The sensing characteristics of plasmonic waveguide with a ring resonator. Opt. Express 2014, 22, 7669–7677. [Google Scholar] [CrossRef] [PubMed]
- Tang, B.; Wang, J.; Xia, X.; Liang, X.; Song, C.; Qu, S. Plasmonic induced transparency and unidirectional control based on the waveguide structure with quadrant ring resonators. Appl. Phys. Express 2015, 8, 032202. [Google Scholar] [CrossRef]
- Han, Z.; Bozhevolnyi, S. Plasmon-induced transparency with detuned ultracompact fabry-perot resonators in integrated plasmonic devices. Opt. Express 2011, 19, 3251–3257. [Google Scholar] [CrossRef] [PubMed]







© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, S.; Song, C.; Xia, X.; Liang, X.; Tang, B.; Hu, Z.-D.; Wang, J. Detuned Plasmonic Bragg Grating Sensor Based on a Defect Metal-Insulator-Metal Waveguide. Sensors 2016, 16, 784. https://doi.org/10.3390/s16060784
Qu S, Song C, Xia X, Liang X, Tang B, Hu Z-D, Wang J. Detuned Plasmonic Bragg Grating Sensor Based on a Defect Metal-Insulator-Metal Waveguide. Sensors. 2016; 16(6):784. https://doi.org/10.3390/s16060784
Chicago/Turabian StyleQu, Shinian, Ci Song, Xiushan Xia, Xiuye Liang, Baojie Tang, Zheng-Da Hu, and Jicheng Wang. 2016. "Detuned Plasmonic Bragg Grating Sensor Based on a Defect Metal-Insulator-Metal Waveguide" Sensors 16, no. 6: 784. https://doi.org/10.3390/s16060784
APA StyleQu, S., Song, C., Xia, X., Liang, X., Tang, B., Hu, Z.-D., & Wang, J. (2016). Detuned Plasmonic Bragg Grating Sensor Based on a Defect Metal-Insulator-Metal Waveguide. Sensors, 16(6), 784. https://doi.org/10.3390/s16060784





