Classification of Kiwifruit Grades Based on Fruit Shape Using a Single Camera
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Preparation and Image Acquisition
2.2. Image Pre-Processing and Segmentation
2.3. Extracting and Calculating Shape Parameters
2.4. Class Definition
2.5. Fruit Volume Estimation
3. Results and Discussion
3.1. Typical Physical Properties
3.2. Fruit Sizes Measured by Image Processing Method
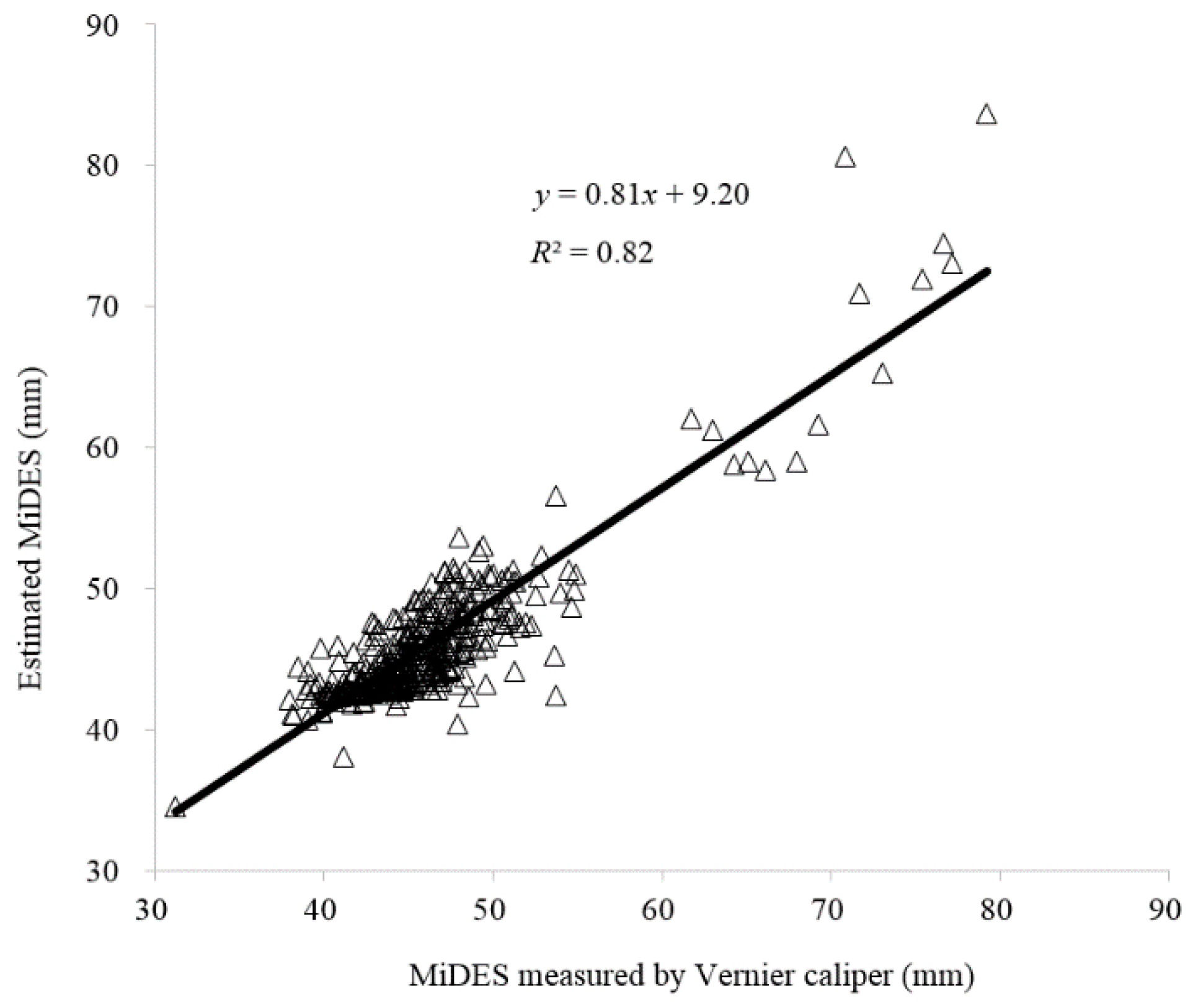
3.3. MiDES Estimation
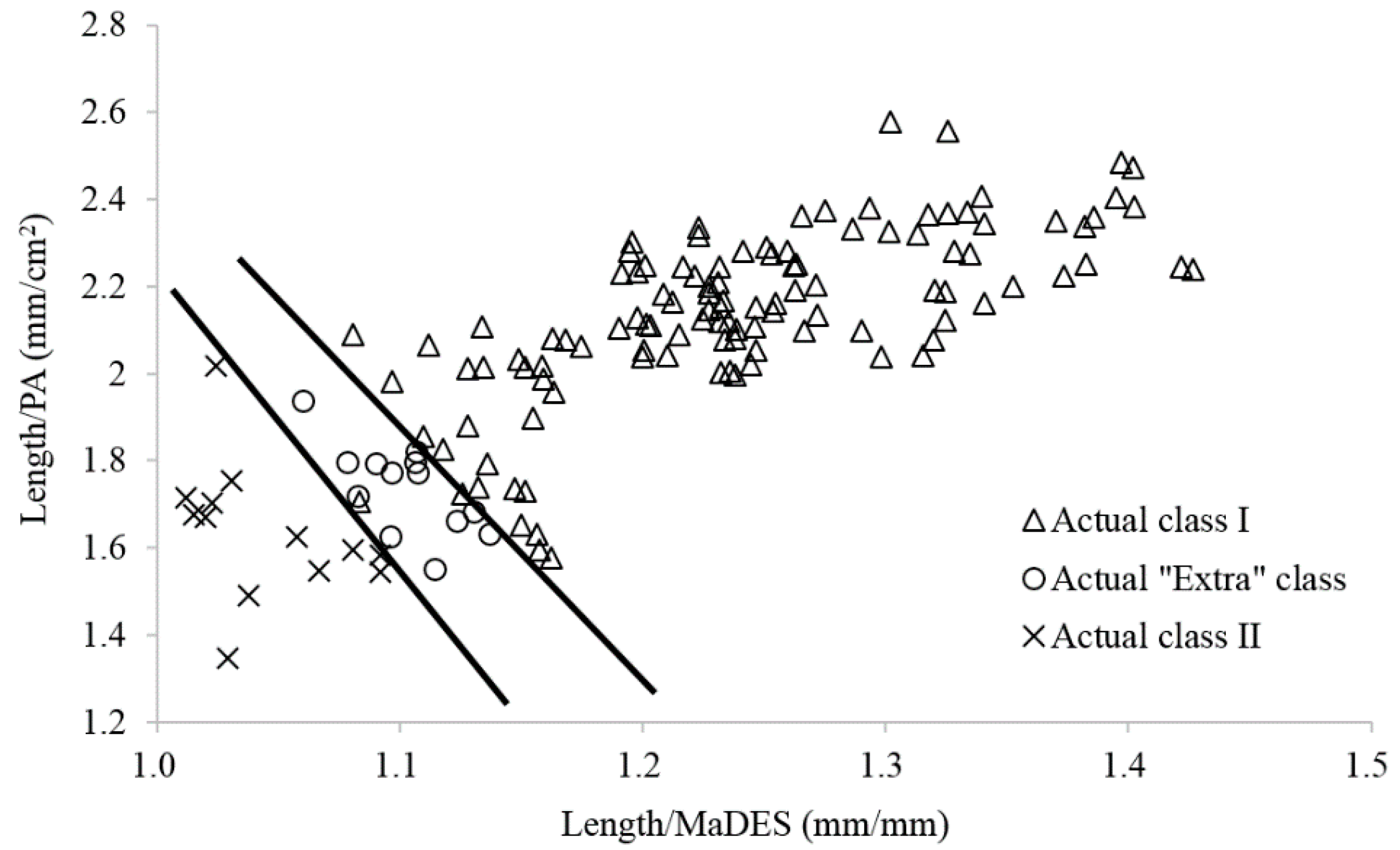
3.4. Fruit Classification
3.5. Volume Estimation
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| Nomenclature | |
| MaDES | maximum diameter of the equatorial section of fruit |
| MiDES | minimum diameter of the equatorial section of fruit |
| MiDESest | estimated MiDES |
| MLR | MaDES to length ratio |
| MMR | MiDES to MaDES ratio |
| PA | projected area of fruit |
| PL | pixel number of fruit length |
| PPA | pixel number of projected area of fruit |
| PW | pixel number of fruit width |
| R2 | coefficient of determination |
| RA | ratio of 1 mm2 to pixels counted from the number of pixels in the smallest square of 1 mm × 1 mm on the coordinate paper |
| RGB | color intensity values of red, green and blue |
| SD | standard deviation |
| SMLR | stepwise multiple linear regression method |
| WDM | water displacement method for measuring fruit volume |
References
- Razavi, S.M.A.; BahramParvar, M. Some physical and mechanical properties of kiwifruit. Int. J. Food Eng. 2007, 3, 1–16. [Google Scholar] [CrossRef]
- Burdon, J.; Punter, M.; Billing, D.; Pidakala, P.; Kerr, K. Shrivel development in kiwifruit. Postharvest Biol. Technol. 2014, 87, 1–5. [Google Scholar] [CrossRef]
- Fu, L.; Wang, B.; Cui, Y.; Su, S.; Gejima, Y.; Kobayashi, T. Kiwifruit recognition at nighttime using artificial lighting based on machine vision. Int. J. Agric. Biol. Eng. 2015, 8, 52–59. [Google Scholar]
- Wang, J.; Liang, Y.; Bai, Q.; Guo, M. Study on Risk Zoning of High Temperature and Drought Disaster for Kiwifruit in Shaanxi. China Agric. Sci. Bull. 2013, 29, 105–110. [Google Scholar]
- Zhang, J.; Mo, Z.; Huang, S.; Guo, Z. Development of kiwifruit industry in the world and analysis of trade and international competitiveness in China entering 21st century. China Agric. Sci. Bull. 2014, 30, 48–55. [Google Scholar]
- Narendra, V.; Hareesha, K. Quality inspection and grading of agricultural and food products by computer vision-A Review. Int. J. Comput. Appl. 2010, 2, 43–65. [Google Scholar] [CrossRef]
- Fadilah, N.; Mohamad-Saleh, J.; Halim, Z.A.; Ibrahim, H.; Ali, S.S.S. Intelligent Color Vision System for Ripeness Classification of Oil Palm Fresh Fruit Bunch. Sensors 2012, 12, 14179–14195. [Google Scholar] [CrossRef] [PubMed]
- Blasco, J.; Aleixos, N.; Molto, E. Machine vision system for automatic quality grading of fruit. Biosyst. Eng. 2003, 85, 415–423. [Google Scholar] [CrossRef]
- Venkatesh, G.V.; Iqbal, S.M.; Gopal, A.; Ganesan, D. Estimation of volume and mass of axi-symmetric fruits using image processing technique. Int. J. Food Proper. 2015, 18, 608–626. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Wu, L.N. Classification of Fruits Using Computer Vision and a Multiclass Support Vector Machine. Sensors 2012, 12, 12489–12505. [Google Scholar] [CrossRef] [PubMed]
- Arjenaki, O.O.; Moghaddam, P.A.; Motlagh, A.M. Online tomato sorting based on shape, maturity, size, and surface defects using machine vision. Turk. J. Agric. For. 2013, 37, 62–68. [Google Scholar]
- Clement, J.; Novas, N.; Gazquez, J.A.; Manzano-Agugliaro, F. High speed intelligent classifier of tomatoes by colour, size and weight. Span. J. Agric. Res. 2012, 10, 314–325. [Google Scholar] [CrossRef]
- ElMasry, G.; Cubero, S.; Molto, E.; Blasco, J. In-line sorting of irregular potatoes by using automated computer-based machine vision system. J. Food Eng. 2012, 112, 60–68. [Google Scholar] [CrossRef]
- Al-Mallahi, A.; Kataoka, T.; Okamoto, H.; Shibata, Y. Detection of potato tubers using an ultraviolet imaging-based machine vision system. Biosyst. Eng. 2010, 105, 257–265. [Google Scholar] [CrossRef]
- Xu, L.; Zhao, Y. Automated strawberry grading system based on image processing. Comput. Electron. Agric. 2010, 71, S32–S39. [Google Scholar]
- Rashidi, M.; Seyfi, K. Classification of fruit shape in kiwifruit applying the analysis of outer dimensions. Int. J. Agric. Biol. 2007, 5, 759–762. [Google Scholar]
- East African Community. Fresh Kiwifruit—Specification and Grading; East African Community: Arusha, Tanzania, 2010. [Google Scholar]
- United Nations. UNECE STANDARD FFV-46 Concerning the Marketing and Commercial Quality Control of KIWIFRUIT; United Nations: Geneva, Switzerland, 2010. [Google Scholar]
- Ministry of Agriculture of the People’s Republic of China. Standards for Grades of Kiwifruits; China Agricultural Publisher: Beijing, China, 2009. [Google Scholar]
- Market and Quality Supervision Commission of Shenzhen Municipality. Purchase and Sale Requirements of Kiwifruit for Pre-Packing Fresh Market; Market and Quality Supervision Commission of Shenzhen Municipality: Shenzhen, China, 2006. [Google Scholar]
- Chen, X.; Yue, T.; Yang, G. Research advances in non-destructive prediction technologies using VIS/NIR spectroscopy for kiwifruit property. Trans. China Soc. Agric. Eng. 2006, 22, 240–245. [Google Scholar]
- Shao, Y.; Xu, L.; Song, S.; Qi, K.; Cui, Y.; Fu, L. Situation and development for kiwifruit grading in the A region of Shaanxi province. J. Agric. Mech. Res. 2015, 37, 249–253. [Google Scholar]
- Poynton, C.A. A Technical Introduction to Digital Video; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1975, 11, 23–27. [Google Scholar]
- Parker, J.R. Algorithms for Image Processing and Computer Vision; John Wiley & Sons: New York, NY, USA, 2010. [Google Scholar]
- Wu, X.; Wang, D.; Sheng, H. An Algorithm and Implementaion for Obtaining Minimum Exterior Rectangle of Image Region. Comput. Eng. 2004, 30, 124–125. [Google Scholar]
- Tabatabaeefar, A.; Vefagh-Nematolahee, A.; Rajabipour, A. Modeling of orange mass based on dimensions. J. Agric. Sci. Technol. 2010, 2, 299–305. [Google Scholar]
- Koc, A.B. Determination of watermelon volume using ellipsoid approximation and image processing. Postharvest Biol. Technol. 2007, 45, 366–371. [Google Scholar] [CrossRef]
- McGlone, V.A.; Jordan, R.B.; Seelye, R.; Martinsen, P.J. Comparing density and NIR methods for measurement of kiwifruit dry matter and soluble solids content. Postharvest Biol. Technol. 2002, 26, 191–198. [Google Scholar] [CrossRef]
- Jarimopas, B.; Nunak, T.; Nunak, N. Electronic device for measuring volume of selected fruit and vegetables. Postharvest Biol. Technol. 2005, 35, 25–31. [Google Scholar] [CrossRef]
- Rashidi, M.; Gholami, M. Determination of kiwifruit volume using ellipsoid approximation and image-processing methods. Int. J. Agric. Biol. 2008, 10, 375–380. [Google Scholar]
- Fu, L.; Song, S.; Shao, Y.; Li, P.; Wang, H.; Cui, Y. Comprhensive evaluation of kiwifruit quality based on principal component and cluster analysis. Food Sci. 2014, 35, 6–10. [Google Scholar]
- Lorestani, A.N.; Tabatabaeefar, A. Modelling the mass of kiwi fruit by geometrical attributes. Int. Agrophys. 2006, 20, 135–139. [Google Scholar]
- Li, P. Automatic Grading Method of Kiwifruit Based on Machine Vsion Technology; Northwest A&F University: Yangling, China, 2013. [Google Scholar]
- Chalidabhongse, T.; Yimyam, P.; Sirisomboon, P. 2D/3D Vision-Based Mango’s Feature Extraction and Sorting. In Proceedings of the 9th International Conference on Control, Automation, Robotics and Vision, Singapore, 5–8 December 2006.
- Tabatabaeefar, A.; Rajabipour, A. Modeling the mass of apples by geometrical attributes. Sci. Hortic. 2005, 105, 373–382. [Google Scholar] [CrossRef]
- Chakespari, A.; Rajabipour, A.; Mobli, H. Mass modeling of two apple varieties by geometrical attributes. Aust. J. Agric. Eng. 2010, 1, 112–118. [Google Scholar]
- Omid, M.; Khojastehnazhand, M.; Tabatabaeefar, A. Estimating volume and mass of citrus fruits by image processing technique. J. Food Eng. 2010, 100, 315–321. [Google Scholar] [CrossRef]
- Sabzi, S.; Javadikia, P.; Rabani, H.; Adelkhani, A. Mass modeling of Bam orange with ANFIS and SPSS methods for using in machine vision. Measurement 2013, 46, 3333–3341. [Google Scholar] [CrossRef]
- Schulze, K.; Nagle, M.; Spreer, W.; Mahayothee, B.; Müller, J. Development and assessment of different modeling approaches for size-mass estimation of mango fruits (Mangifera indica L., cv. ‘Nam Dokmai’). Comput. Electron. Agric. 2015, 114, 269–276. [Google Scholar] [CrossRef]
- Spreer, W.; Müller, J. Estimating the mass of mango fruit (Mangifera indica, cv. Chok Anan) from its geometric dimensions by optical measurement. Comput. Electron. Agric. 2011, 75, 125–131. [Google Scholar] [CrossRef]





| Classes | No. | W (g) | L (mm) | MaDES (mm) | MiDES (mm) | MiDESest (mm) | PA(cm2) | V (cm3) | Vest (cm3) | MLR (%) | MMR (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| “Extra” class | 163 | 113.0 ± 15.0 a,* | 70.9 ± 7.5 a | 56.9 ± 6.6 a | 49.9 ± 7.0 a | 49.0 ± 6.5 a | 37.8 ± 4.4 a | 108.7 ± 14.9 a | 108.8 ± 14.4 a | 80.3 ± 4.9 a | 87.7 ± 5.2 a |
| Class I | 157 | 90.7 ± 19.0 b | 63.6 ± 4.7 b | 52.4 ± 5.3 b | 44.1 ± 2.2 b | 44.7 ± 2.4 b | 31.7 ± 5.8 b | 86.5 ± 18.5 b | 87.4 ± 18.1 b | 82.4 ± 6.1 a,b | 84.9 ± 7.8 a |
| Class II | 133 | 80.8 ± 28.2 b | 59.4 ± 4.6 c | 51.4 ± 10.6 b | 42.5 ± 3.1 b | 42.9 ± 2.2 b | 29.1 ± 9.1 b | 77.5 ± 27.1 b | 77.8 ± 26.6 b | 86.1 ± 13.7 b | 85.2 ± 13.5 a |
| “Reject” class | 37 | 64.0 ± 0.7 c | 58.8 ± 2.6 c | 47.1 ± 3.3 c | 41.4 ± 3.4 c | 41.5 ± 0.7 c | 24.3 ± 0.7 c | 61.8 ± 2.4 c | 62.1 ± 0.7 c | 80.4 ± 5.9 a | 87.9 ± 5.5 a |
| Total | 490 | 97.9 ± 23.6 | 65.9 ± 7.5 | 54.1 ± 7.5 | 46.2 ± 5.8 | 46.1 ± 5.2 | 33.7 ± 7.0 | 93.9 ± 22.9 | 94.1 ± 22.6 | 82.1 ± 7.7 | 86.2 ± 8.2 |
| Parameters | Coefficients | t | Significance |
|---|---|---|---|
| Weight (g) | −0.08 | −6.36 | 0.00 |
| PA (cm2) | −3.71 × 10−4 | −0.69 | 0.49 |
| Length (mm) | 0.66 | 18.72 | 0.00 |
| MaDES (mm) | 0.24 | 6.02 | 0.00 |
| Constant | −2.36 | - | - |
| Estimated Class | “Extra” Class | Class I | Class II | “Reject” Class | |||
|---|---|---|---|---|---|---|---|
| Actual Class | “Extra” Class | Class I | “Extra” Class | Class I | Class II | Class II | “Reject” Class |
| Fruit samples | 103 | 28 | 13 | 85 | 13 | 82 | 26 |
| Weight/Length | 1.58 ± 0.15 a,* | 1.62 ± 0.13 a | 1.74 ± 0.13 a,* | 1.37 ± 0.19 b | 1.81 ± 0.17 a | 1.29 ± 0.36 | 1.09 ± 0.04 |
| Weight/PA | 2.98 ± 0.15 a | 2.92 ± 0.11 a | 3.02 ± 0.16 a | 2.84 ± 0.10 a | 2.86 ± 0.15 a | 2.75 ± 0.12 | 2.64 ± 0.08 |
| Weight/MaDES | 1.99 ± 0.21 a | 1.94 ± 0.18 a | 1.95 ± 0.18 a | 1.67 ± 0.17 b | 1.84 ± 0.20 a | 1.51 ± 0.17 | 1.36 ± 0.09 |
| Length/MaDES | 1.26 ± 0.05 a | 1.18 ± 0.04 b | 1.12 ± 0.03 a | 1.23 ± 0.07 b | 1.02 ± 0.03 c | 1.20 ± 0.15 | 1.25 ± 0.10 |
| Length/PA | 1.89 ± 0.17 a | 1.81 ± 0.11 b | 1.74 ± 0.05 a | 2.10 ± 0.21 b | 1.58 ± 0.11 c | 2.22 ± 0.34 | 2.42 ± 0.10 |
| MaDES/PA | 1.51 ± 0.16 a | 1.51 ± 0.10 a | 1.56 ± 0.09 a | 1.71 ± 0.13 b | 1.54 ± 0.14 a | 1.84 ± 0.14 | 1.94 ± 0.12 |
| Parameters | Coefficients | t | Significance |
|---|---|---|---|
| Weight (g) | 0.93 | 134.16 | 0.00 |
| PA (cm2) | 5.47 × 10−5 | 0.2147 | 0.83 |
| Length (mm) | 0.09 | 4.27 | 0.02 |
| MaDES (mm) | 1.65 × 10−3 | 0.46 | 0.62 |
| Constant | −2.69 | - | - |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, L.; Sun, S.; Li, R.; Wang, S. Classification of Kiwifruit Grades Based on Fruit Shape Using a Single Camera. Sensors 2016, 16, 1012. https://doi.org/10.3390/s16071012
Fu L, Sun S, Li R, Wang S. Classification of Kiwifruit Grades Based on Fruit Shape Using a Single Camera. Sensors. 2016; 16(7):1012. https://doi.org/10.3390/s16071012
Chicago/Turabian StyleFu, Longsheng, Shipeng Sun, Rui Li, and Shaojin Wang. 2016. "Classification of Kiwifruit Grades Based on Fruit Shape Using a Single Camera" Sensors 16, no. 7: 1012. https://doi.org/10.3390/s16071012
APA StyleFu, L., Sun, S., Li, R., & Wang, S. (2016). Classification of Kiwifruit Grades Based on Fruit Shape Using a Single Camera. Sensors, 16(7), 1012. https://doi.org/10.3390/s16071012






