Development of Torque Sensor with High Sensitivity for Joint of Robot Manipulator Using 4-Bar Linkage Shape
Abstract
:1. Introduction
2. Torque Sensor with High Sensitivity
3. Simulation
3.1. Finite Element Analysis Model
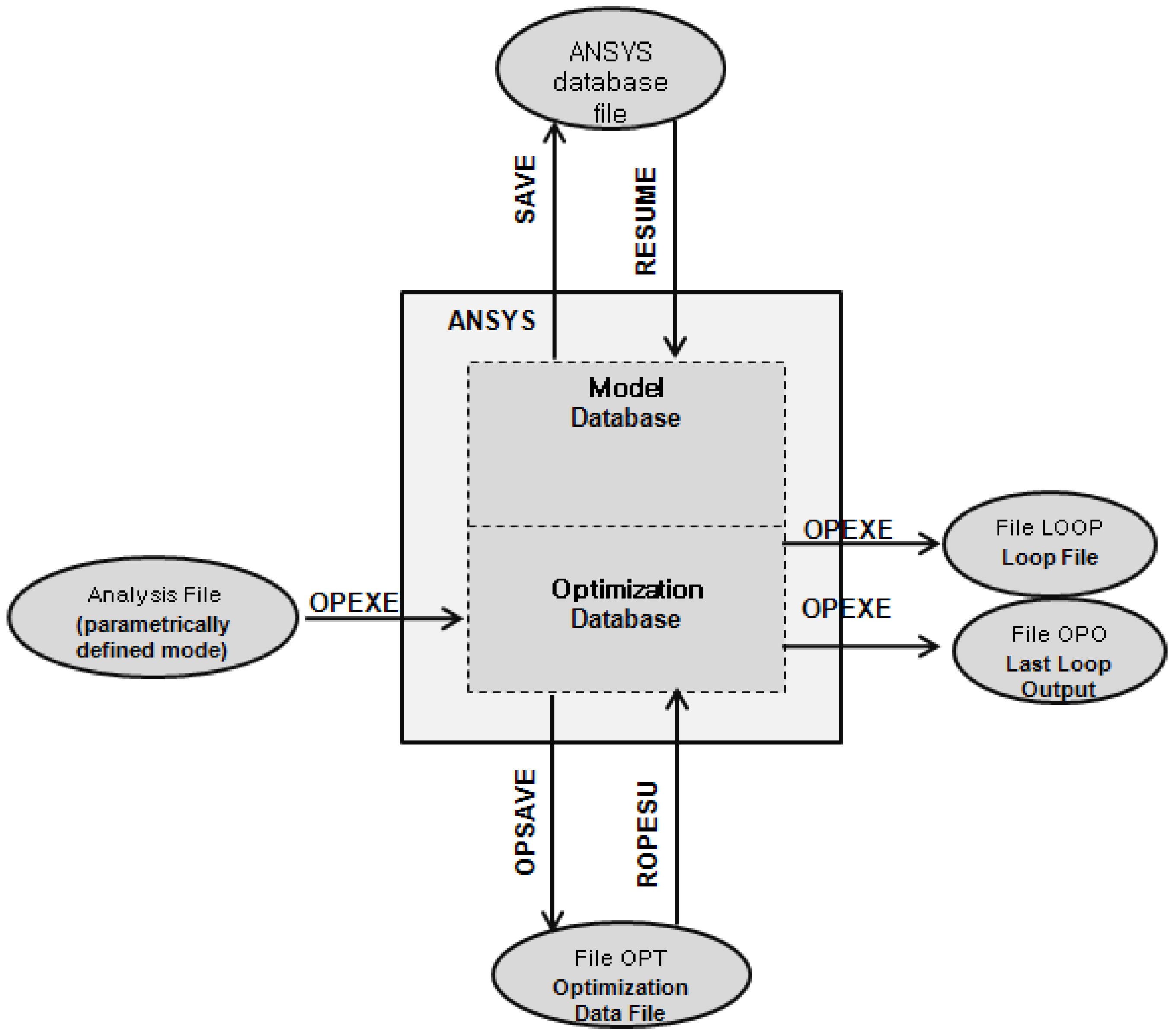
3.2. The Optimization
3.3. FEA Results
4. Experimental Results
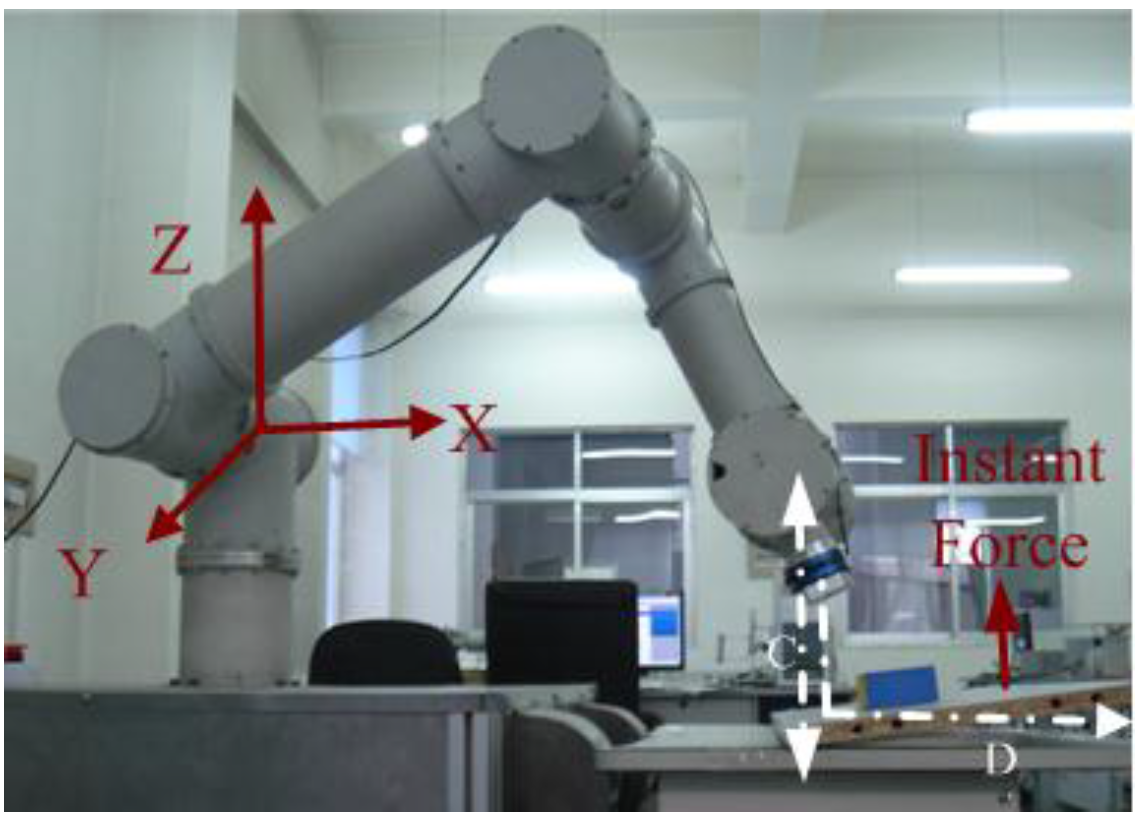
4.1. Experimental Equipment
4.2. Experimental Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kosuge, K.; Takeuchi, H.; Furuta, K. Motion control of a robot arm using joint torque sensors. IEEE Trans. Robot. Autom. 1990, 6, 258–263. [Google Scholar] [CrossRef]
- Craig, J.J. Introduction to Robotics: Mechanics and Control, 3rd ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2005; pp. 156–157. [Google Scholar]
- Xia, J.; Xie, Z.; Fang, H.; Lan, T.; Huang, J.; Liu, H. Collision detection of flexible joint manipulator by using joint torque sensors. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Suntec Convention and Exhibition Center, Singapore, 14–17 July 2009; pp. 1816–1821.
- Albu-Schäffer, A.; Haddadin, S.; Ott, C.; Stemmer, A.; Wimböck, T.; Hirzinger, G. The DLR lightweight robot: Design and control concepts for robots in human environments. Ind. Robot Int. J. 2007, 34, 376–385. [Google Scholar]
- Aghili, F.; Buehler, M.; Hollerbach, J.M. Sensing the torque in a robot’s joint. ASME Mech. Eng. 1998, 120, 66–69. [Google Scholar]
- Haddadin, S.; Albu-Schäffer, A.; Luca, A.; Hirzinger, G. Collision Detection and Reaction: A Contribution to Safe Physical Human-Robot Interaction. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Acropolis Convention Center, Nice, France, 22–26 September 2008; pp. 3356–3363.
- Patel, R.V.; Talebi, H.A.; Jayender, J.; Shadpey, F. A robust position and force control strategy for 7-DOF redundant manipulators. IEEE/ASME Trans. Mechatron. 2009, 14, 575–589. [Google Scholar] [CrossRef]
- Zhang, G.; Furusho, J. Control of robot arms using joint torque sensors. IEEE Control Syst. 1998, 18, 48–55. [Google Scholar] [CrossRef]
- Wu, C.H.; Paul, R.P. Manipulator compliance based on joint torque control. In Proceedings of the IEEE Conference on Decision and Control including the Symposium on Adaptive Processes, Albuquerque, NM, USA, 10–12 December 1980; pp. 88–94.
- Luh, J.Y.S.; Fisher, W.D.; Paul, R.P.C. Joint torque control by a direct feedback for industrial robot. IEEE Trans. Autom. Control. 1983, 28, 153–161. [Google Scholar] [CrossRef]
- Vischer, D.; Khatib, O. Design and development of high-performance torque controlled joints. IEEE Trans. Robot. Autom. 1995, 11, 537–544. [Google Scholar] [CrossRef]
- Joo, J.W.; Kang, D.I. Analysis and design of the hollow cruciform-type torque sensor. In Proceedings of the Spring Conference on the Korean Society of Mechanical Engineers, Daejeon, Korea, 21 April 1994; pp. 311–315.
- Aghili, F.; Buehler, M.; Hollerbach, J. Design of a Hollow Hexaform Torque Sensor for Robot Joints. Int. J. Robot. Res. 2001, 20, 967–976. [Google Scholar] [CrossRef]
- Tsetserukou, D.; Tadakuma, R.; Kajimoto, H.; Tachi, S. Optical Torque Sensors for Implementation of Local Impedance Control of the Arm of Humanoid Robot. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; pp. 1674–1679.
- Gao, X.H.; Jin, M.H.; Xie, Z.W.; Jiang, L.; Ni, F.L.; Shi, S.C.; Wei, R.; Zhu, Y.Y.; Cai, H.G.; Liu, H.; et al. Development of the Chinese intelligent space robotic system. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 994–1001.
- Hirzinger, G.; Brunner, B.; Landzettel, K.; Sporer, N.; butterfaß, J.; Schedl, M. Space Robotics—DLR’s Telerobotic Concepts, Lightweight Arms and Articulated Hands. Auton. Robot. 2003, 14, 127–145. [Google Scholar] [CrossRef]
- Uicker, J.J., Jr.; Pennock, G.R.; Shigley, J.E. Theory of Machines and Mechanisms, 3rd ed.; Oxford University Press: Oxford, UK, 2003; pp. 126–127. [Google Scholar]
- Harmonic Drive Systems, Inc. HarmonicDrive General Catalog; Harmonic Drive, Inc.: Tokyo, Japan, 2015. [Google Scholar]
- ANSYS, Inc. ANSYS Mechanical APDL Theory Reference; ANSYS, Inc.: Canonsburg, PA, USA, 2010. [Google Scholar]
- NI, Inc. LabVIEW; NI, Inc.: Austin, TX, USA, 2015. [Google Scholar]






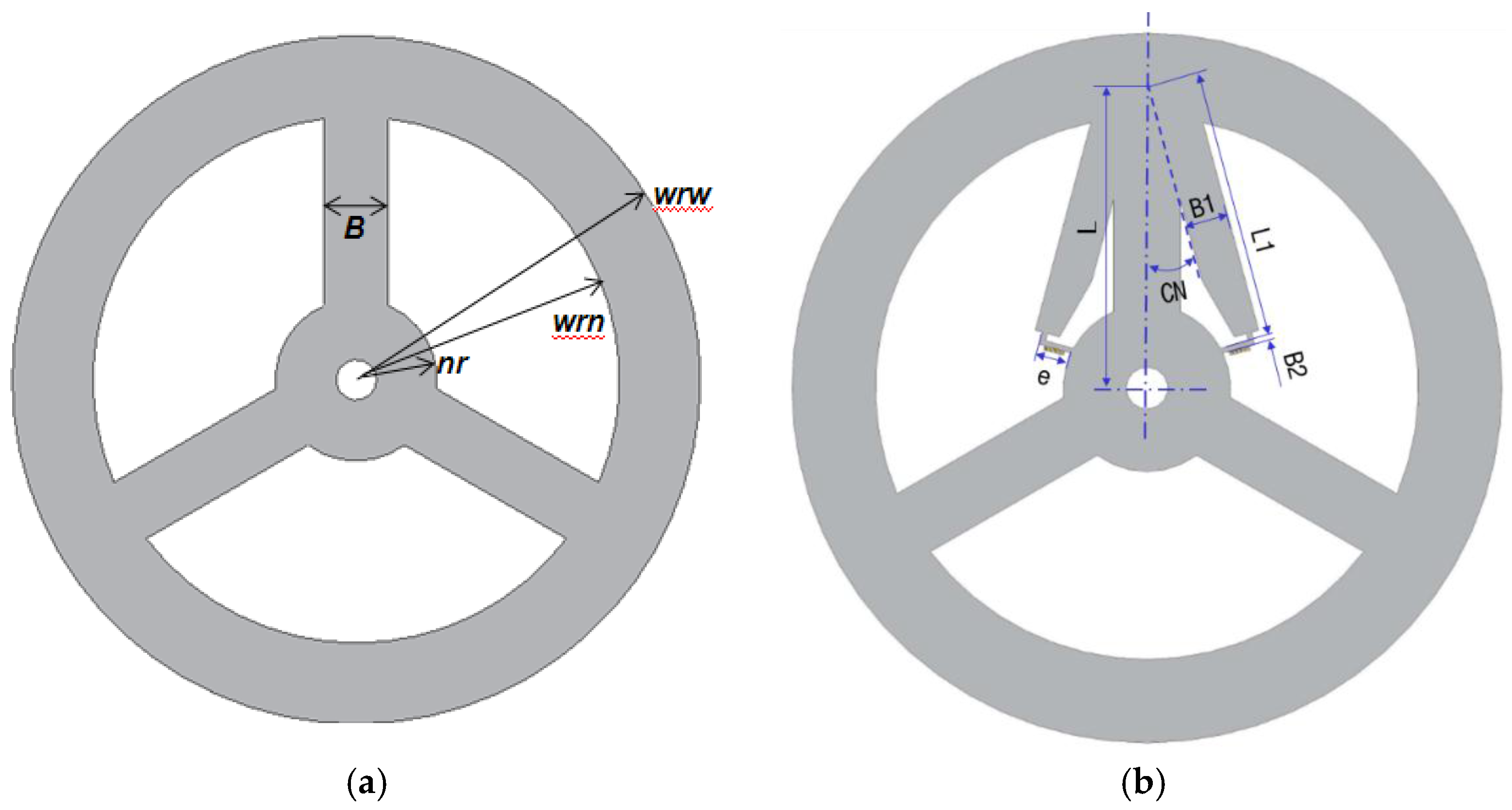





| 3 Beams | TSHS | ||||
|---|---|---|---|---|---|
| Initial Value | Lower Limit | Upper Limit | |||
| Fixed Parameter | wrw (mm) | 75 | |||
| wrn (mm) | 60 | ||||
| nr (mm) | 20 | ||||
| B (mm) | 10 | ||||
| e (mm) | - | 4.5 | |||
| DV | L (mm) | - | 64 | 63 | 70 |
| B1 (mm) | - | 5.0 | 3.8 | 6.0 | |
| L1 (mm) | - | 47.5 | 45 | 50 | |
| B2 (mm) | - | 0.5 | 0.4 | 0.6 | |
| CN (deg) | - | 15 | 14 | 15.5 | |
| 3 Beams | TSHS | |||
|---|---|---|---|---|
| Initial Value | Optimal Result | |||
| DV | L (mm) | - | 64 | 65 |
| B1 (mm) | - | 5.0 | 5.0 | |
| L1 (mm) | - | 47.5 | 47.5 | |
| B2 (mm) | - | 0.5 | 0.55 | |
| CN (deg) | - | 15 | 15 | |
| SV | 3.51 × 10−4 | 6.70 × 10−4 | 12.2 × 10−4 | |
| (rad) | 21.6 × 10−4 | 21.6 × 10−4 | 19.8 × 10−4 | |
| OV | 3.51 × 10−4 | 6.70 × 10−4 | 12.2 × 10−4 | |
| 0.163 | 0.310 | 0.615 | ||
| Parameters | Contents |
|---|---|
| Strain gauge type | KFG-02-120-C123L1M2R |
| Gauge Factor | 2.25 ± 1.0% |
| Gauge Resistance | 119.6 ± 0.4 Ω |
| Gauge size | 3.3 × 2.4 mm |
| Name | Method | Strain | Deflection (rad) | λ |
|---|---|---|---|---|
| 3 beams | FEM | 3.51 × 10−4 | 21.6 × 10−4 | 0.163 |
| Experiment | 3.48 × 10−4 | 22.0 × 10−4 | 0.158 | |
| Error | −0.85% | 1.85% | −2.66% | |
| TSHS | FEM | 12.2 × 10−4 | 19.8 × 10−4 | 0.615 |
| Experiment | 12.3 × 10−4 | 20.5 × 10−4 | 0.601 | |
| Error | 1.40% | 3.80% | −2.31% | |
| FEM | 3.48 | 0.916 | 3.77 | |
| Experiment | 3.53 | 0.932 | 3.80 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.-X.; Ryoo, Y.-J.; Byun, K.-S. Development of Torque Sensor with High Sensitivity for Joint of Robot Manipulator Using 4-Bar Linkage Shape. Sensors 2016, 16, 991. https://doi.org/10.3390/s16070991
Zhang H-X, Ryoo Y-J, Byun K-S. Development of Torque Sensor with High Sensitivity for Joint of Robot Manipulator Using 4-Bar Linkage Shape. Sensors. 2016; 16(7):991. https://doi.org/10.3390/s16070991
Chicago/Turabian StyleZhang, Hong-Xia, Young-Jae Ryoo, and Kyung-Seok Byun. 2016. "Development of Torque Sensor with High Sensitivity for Joint of Robot Manipulator Using 4-Bar Linkage Shape" Sensors 16, no. 7: 991. https://doi.org/10.3390/s16070991
APA StyleZhang, H.-X., Ryoo, Y.-J., & Byun, K.-S. (2016). Development of Torque Sensor with High Sensitivity for Joint of Robot Manipulator Using 4-Bar Linkage Shape. Sensors, 16(7), 991. https://doi.org/10.3390/s16070991






