An Anonymous User Authentication and Key Agreement Scheme Based on a Symmetric Cryptosystem in Wireless Sensor Networks
Abstract
:1. Introduction
1.1. Related Studies
1.2. Motivations and Contributions
1.3. The Threat Model
- (1)
- (2)
- An attacker can modify and resend the intercepted/eavesdropped message [37].
- (3)
- All of the existing smart cards are vulnerable, because the confidential information that is stored within them can be extracted by physically monitoring the power consumption [38], meaning that an attacker could read the data that is stored on a smart card.
- (4)
- (5)
- An attacker can easily guess low-entropy passwords and identities in an off-line manner, but the guessing of two secret parameters (e.g., password, identity) is computationally infeasible in polynomial time [39].
1.4. Security Requirements for User Authentication Scheme
- (1)
- User anonymity: A user’s identity should be protected even if an attacker exploits user’s smart card used for authentication scheme or if the messages which exchanged in communication group are exposed.
- (2)
- Mutual authentication: Mutual authentication should be carried out between the user and gateway node, the gateway node and sensor node, and the sensor node and user, respectively.
- (3)
- Session key agreement: The session key should be securely shared among other communication parties after the verification procedure is finished.
- (4)
- Quick detection of the incorrect password: If a user enters the incorrect password by mistake in login phase, the password should be detected before performing verification phase.
- (5)
- User friendliness: This property allows users to freely change/update their password without needing to communicate with the gateway node.
- (6)
- Robustness: User authentication schemes should withstand different types of attacks.
- Smart card loss attacks: If an attacker steals a user’s smart card, the attacker can extract the contents by the power consumption technique [38]. With obtained information, the attacker can try to launch various types of attacks.
- Off-line identity/password guessing attacks: An attacker tries to guess a identity/password and eventually find out the exact identity/password in an off-line environment by using the information stored in the smart card.
- User impersonation attacks: An attacker pretends to be the registered user with the forged login message by using the secret or public information that is collected from the smart cards and the data packets.
- Replay attacks: An attacker intercepts data packets for the purpose of making use of that data in some manner. Typically, this type of attack connotes copying and possibly modifying the data in various ways.
- Privileged-insider attacks: A privileged-insider attack literally means the attack mounted by a malicious insider. The malicious insiders have a noticeable advantage over external attackers because they have an authorized system admission and also may be familiar with the network design and system actions. Commonly, the malicious insiders want to obtain the users’ private information such as their passwords.
- Denial of Service (DoS) attacks: A DoS attack is any event that diminishes or eliminates a network’s capability of performing its expected function. In other words, an attacker mounts a DoS attack to make the server unavailable.
- Stolen-verifier attacks: An attacker steals a password-verifier from the gateway node and directly use it to masquerade as a legitimate user.
- Gateway node impersonation attacks: An attacker pretends to be the valid gateway node using the captured information.
1.5. Notations
1.6. Organization of the Paper
2. Review of Chen et al.’s Scheme
2.1. Registration Phase
- (1)
- selects and , and then generates a random nonce b that is only known to the . computes a masked password , and sends registration request message to through a secure channel.
- (2)
- computes . chooses a new smart card, and writes into the smart card’s memory. Then, sends the smart card to through a secure channel.
- (3)
- enters the random nonce b in its memory. Finally, the smart card contains the information .
2.2. Login Phase
- (1)
- inserts ’s smart card into a terminal, and inputs the and . The smart card compares with the stored value . If this condition is satisfied, the smart card acknowledges the legitimacy of the , and proceeds with the next step. Otherwise, it terminates this phase.
- (2)
- The smart card computes and , then chooses a random nonce , and computes .
- (3)
- Finally, sends a login request message to through a public channel.
2.3. Verification Phase
- (1)
- first checks the validity of the time-stamp . computes and decrypts . then compares and with the received values. If this condition is satisfied, acknowledges the legitimacy of the and proceeds with the next step. Otherwise, it terminates this phase.
- (2)
- computes and , then sends the message to through a public channel.
- (3)
- checks whether . then computes and . compares with the received value . If this condition is satisfied, believes that the is authentic. Otherwise, it terminates this phase.
- (4)
- computes , and then sends the message to through a public channel.
- (5)
- checks whether . then computes , and compares it with the received value . If true, believes that the is authentic. Otherwise, terminates this phase.
- (6)
- computes , and sends the message to through a public channel.
- (7)
- checks whether . decrypts and compares , and with the previous values. If the verification does not hold, this phase is terminated. Otherwise, the believes that the is authentic, and successfully ends the verification phase.
2.4. Password Change Phase
- (1)
- inserts ’s smart card into a terminal and inputs , the old password and new password . The smart card compares the entered value with the stored in the smart card. If this condition is not satisfied, it terminates this phase. Otherwise, the smart card proceeds with the next step.
- (2)
- The smart card computes , and .
- (3)
- The smart card replaces the existing value with the new value . Finally, the smart card contains the information .
3. Security Weaknesses of Chen et al.’s Scheme
3.1. Smart Card Loss Attack
- Scenario 1:
- If the attacker obtains the smart card, he or she can easily expose a user’s identity through physically monitoring the power consumption [38]. Disclosure of the user’s identity may allow tracking of the ’s behavior and his or her current location.
- Scenario 2:
- Using obtained smart card, the attacker can successfully pass the checking process of the login phase through using the in the smart card, because their checking process just compares the entered with the stored in the smart card. The same situation also happens for the password change phase.
3.2. Denial of Service Attack
- Step 1.
- The attacker inserts the ’s smart card into a terminal, and enters the , and , where and are the attacker’s arbitrary new passwords.
- Step 2.
- The smart card compares the entered value with the stored in the smart card. At this time, it is obvious that this verification process turns out to be successful, since the entered is the same as the stored one in the smart card.
- Step 3.
- The smart card computes , and .
- Step 4.
- The smart card successfully replaces with the new value .
3.3. Failure to Preserve User Anonymity
3.4. Incorrect Password Cannot be Quickly Detected
4. The Proposed Scheme
4.1. Registration Phase
- (1)
- selects and , and then generates a random nonce b, that is only known to the . computes a masked password and sends registration request message to through a secure channel.
- (2)
- computes , and , and stores the v into the database. then chooses a new smart card and writes into the smart card memory. After that the sends the smart card to through a secure channel.
- (3)
- Upon receiving the smart card, enters the random nonce b in its memory. Finally, the smart card contains the information .
4.2. Login Phase
- (1)
- inserts ’s smart card into a terminal, and inputs the and . The smart card computes the masked password and . The smart card further computes , and compares it with the stored value . If this condition is satisfied, the smart card acknowledges the legitimacy of the , and proceeds with the next step. Otherwise, it terminates this phase.
- (2)
- The smart card chooses a random nonce , and computes . The smart card then computes and .
- (3)
- Finally, sends a login request message to through a public channel.
4.3. Verification Phase
- (1)
- first checks the validity of the time-stamp . computes and decrypts . then compares and with the received values. If this condition is satisfied, acknowledges the legitimacy of the and proceeds with the next step. Otherwise, it terminates this phase.
- (2)
- chooses , and computes . further computes and , and then sends the message to through a public channel.
- (3)
- first checks whether . If this condition does not hold, this phase is terminated. Otherwise, it computes and . The further computes and compares it with the received value . If this condition is satisfied, believes that the is authentic. Otherwise, it terminates this phase.
- (4)
- computes , and then sends the message to through a public channel.
- (5)
- first checks whether . If the relationship does not hold, this phase is terminated. Otherwise, it computes , and compares it with the received value . If true, believes that the is authentic. Otherwise, it terminates this phase.
- (6)
- computes , and sends the message to through a public channel.
- (7)
- first checks whether . If the relationship does not hold, it terminates this phase. Otherwise, it computes , and compares , and with the previous values. If the verification does not hold, it terminates this phase. Otherwise, the believes that is authentic, and successfully ends the verification phase.
4.4. Password Change Phase
- (1)
- inserts ’s smart card into a terminal, and inputs , old password , and new password . The smart card computes the old masked password , , and . The smart card then verifies whether . If this condition is not satisfied, it terminates this phase. Otherwise, the smart card proceeds with the next step.
- (2)
- The smart card computes , and
- (3)
- The smart card replaces the existing values and with the new values and , respectively. Finally, the smart card contains the information .
5. Security Analysis and Proof of the Proposed Scheme
5.1. Security Analysis of the Proposed Scheme
5.2. Authentication Proof with BAN Logic
- : The A sees the sentence S.
- : The sentence S is believed by A.
- : It makes a fresh sentence S.
- : The A said the sentence S.
- : Combine the sentence S using K.
- : For secure communication, A and B share a secret key K.
- : The sentence S is controled by A.
- : Encrypt the sentence S using K
- : Perform the hash operation to sentence X using Y.
- Message-meaning rule: : If the key K is shared between A and B, A sees the S combined by K. Then A believes that B once said S.
- Nonce-verification rule: : If A trusts that S is fresh and A believes B once said S, then A believes that B believes S.
- The believe rule: : If S and T are believed by A, then are also believed by A .
- Freshness-conjuncatenation rule: : If freshness of S is believed by A, then A can trust the freshness of whole statement.
- Jurisdiction rule: : If A establishes that B has jurisdiction over S, and A trusts that B trusts a statement S, then A also trusts S.
- Goal 1.
- Goal 2.
- Goal 3.
- Goal 4.
- Message 1. :
- Message 2. :
- Message 3. :
- Message 4. :
- Message 5. :
- Message 6. :
- Message 7. :
- Message 8. :
- A1:
- A2:
- A3:
- A4:
- A5:
- A6:
- A7:
- A8:
- A9:
- A10:
- A11:
- A12:
- A13:
- A14:
- A15:
- A16:
- A17:
- A18:
- A19:
- A20:
- A21:
- A22:
- S1
- S2
- S3
- S4
- S5
- S6
- S7
- S8
- S9
- S10
- S11
- S12
- S13
- S14
- S15
- S16
- S17
- S18
- S19
- S20
- S21
- S22
- S23
- S24
- S25
- S26
- S27
- S28
- S29
- S30
- S31
- S32
- S33
- S34
- S35
- (Goal 4.)
- S36
- (Goal 3.)
- S37
- S38
- S39
- S40
- S41
- S42
- S43
- S44
- S45
- S46
- S47
- (Goal 2.)
- S48
- (Goal 1.)
6. Performance Analysis of the Proposed Scheme
6.1. Computational Performance Analysis
- : the time to execute a one-way hashing operation
- : the time to compute a symmetric-key encryption/decryption
- : the time to compute an encryption/decryption operation in ECC-160 algorithm
6.2. Communication Performance Analysis
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Das et al.’s Authentication Scheme [13]

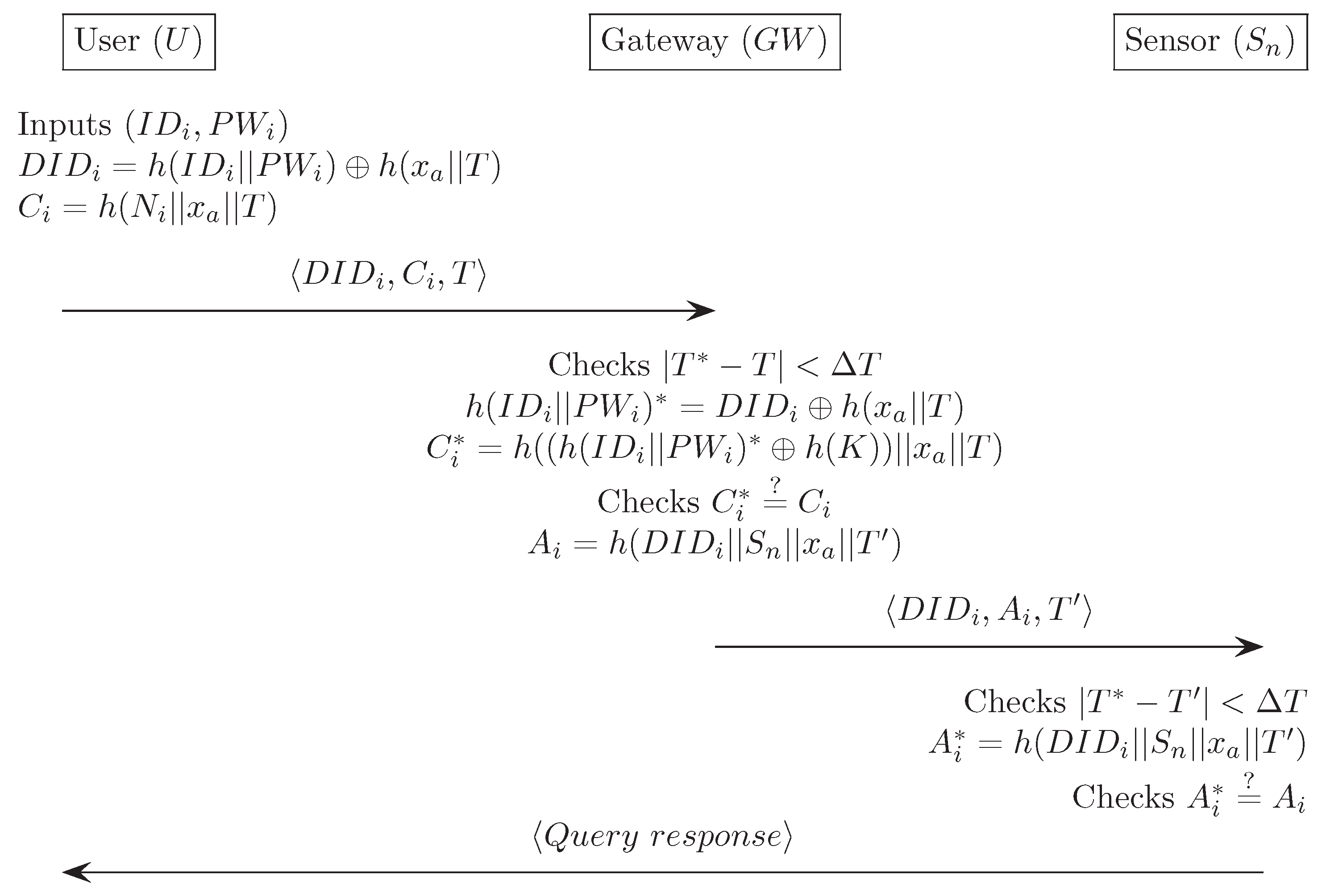
Appendix B. Khan and Alghathbar’s Authentication Scheme [14]


Appendix C. Vaidya et al.’s Authentication Scheme [15]


Appendix D. Chen and Shih’s Authentication Scheme [16]

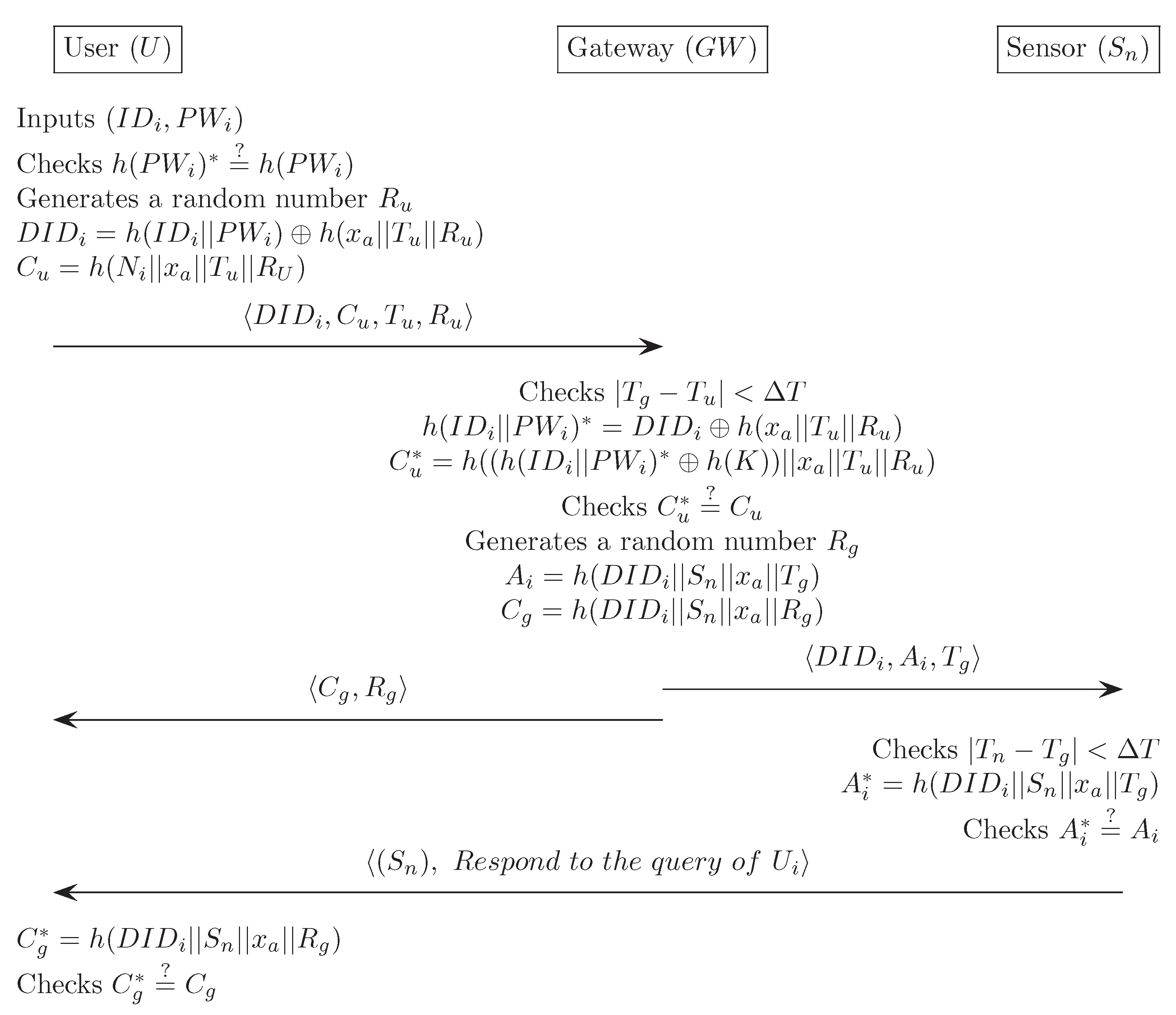
Appendix E. Fan et al.’s Authentication Scheme [17]


Appendix F. Yeh et al.’s Authentication Scheme [18]

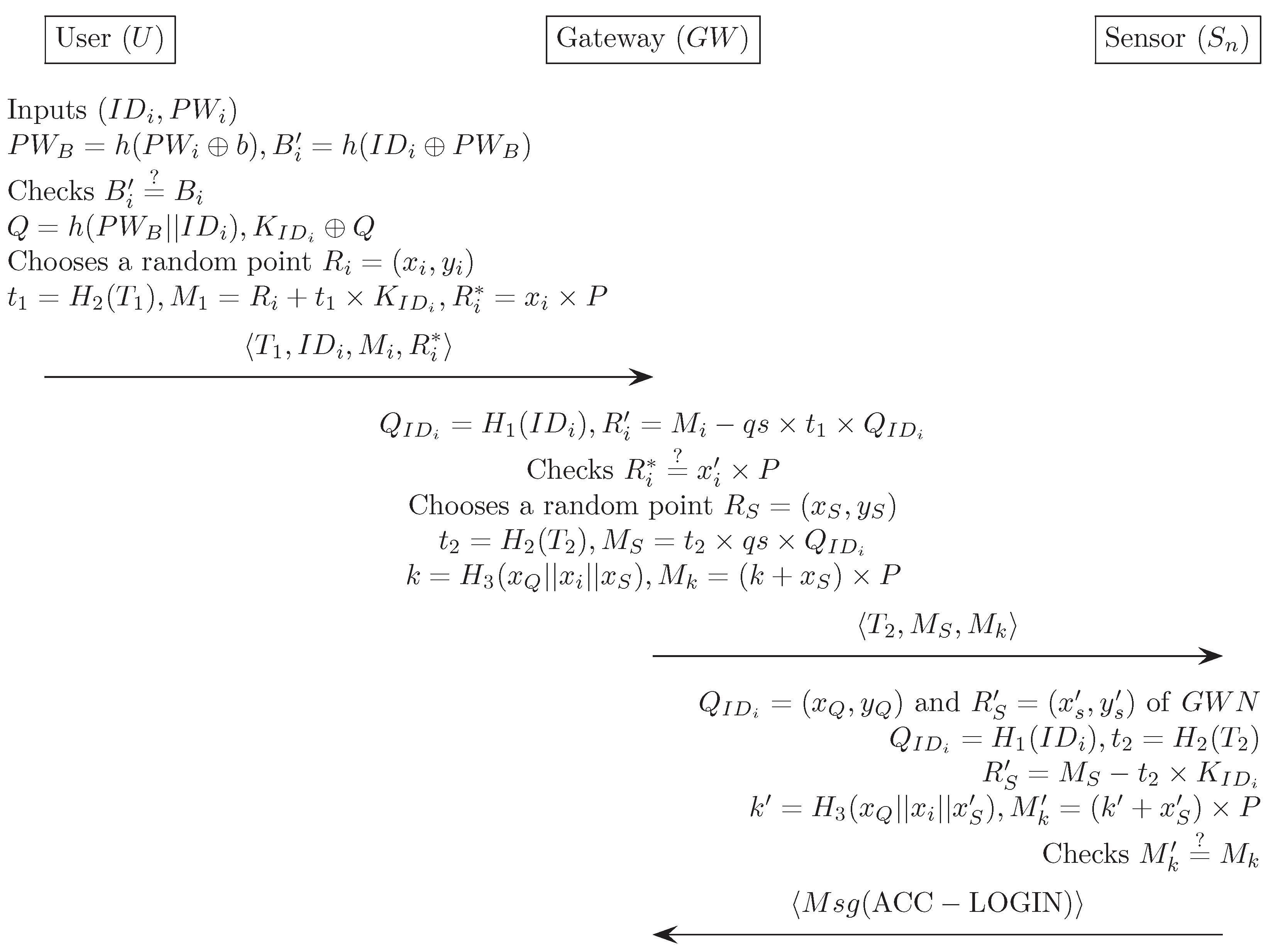
Appendix G. Das et al.’s Authentication Scheme [19]


Appendix H. Xue et al.’s Authentication Scheme [20]


References
- Yick, J.; Mukherjee, B.; Ghosal, D. Wireless sensor network survey. Comput. Netw. 2008, 52, 2292–2330. [Google Scholar] [CrossRef]
- Chong, C.Y.; Kumar, S.P. Sensor networks: evolution, opportunities, and challenges. Proc. IEEE. 2003, 91, 1247–1256. [Google Scholar] [CrossRef]
- Claycomb, W.R.; Shin, D. A novel node level security policy framework for wireless sensor networks. J. Netw. Comput. Appl. 2011, 34, 418–428. [Google Scholar] [CrossRef]
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Watro, R.; Kong, D.; Cuti, S.F.; Gardiner, C.; Lynn, C.; Kruus, P. TinyPK: Securing sensor networks with public key technology. In Proceedings of the 2nd ACM workshop on Security of ad hoc and sensor networks, Washington, DC, USA, 25 October 2004; pp. 59–64.
- Koblitz, N. Elliptic curve cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- ElGamal, T. A public key cryptosystem and a signature scheme based on discrete logarithms. In Workshop on the Theory and Application of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 1984; pp. 10–18. [Google Scholar]
- Hwang, M.S.; Li, L.H. A new remote user authentication scheme using smart cards. IEEE Trans. Consum. Electron. 2000, 46, 28–30. [Google Scholar] [CrossRef]
- Lamport, L. Password authentication with insecure communication. Commun. ACM 1981, 24, 770–772. [Google Scholar] [CrossRef]
- Wong, K.H.; Zheng, Y.; Cao, J.; Wang, S. A dynamic user authentication scheme for wireless sensor networks. In Proceedings of the IEEE International Conference on Sensor Networks, Ubiquitous, and Trustworthy Computing, Taichung, Taiwan, 5–7 June 2006; Volume 1, pp. 1–9.
- Tseng, H.R.; Jan, R.H.; Yang, W. An Improved dynamic user authentication scheme for wireless sensor networks. In Proceedings of the Global Telecommunications Conference, Washington, DC, USA, 26–30 November 2007.
- Vaidya, B.; SáSilva, J.; Rodrigues, J.J.P.C. Robust dynamic user authentication scheme for wireless sensor networks. In Proceedings of the 5th ACM Symposium on QoS and Security for Wireless and Mobile Networks, New York, NY, USA, 28 October 2009; pp. 88–91.
- Das, M.L. Two-factor user authentication scheme in wireless sensor networks. IEEE Trans. Wirel. Commun. 2009, 8, 1086–1090. [Google Scholar] [CrossRef]
- Khan, M.K.; Alghathbar, K. Cryptanalysis and security improvements of two-factor user authentication in wireless sensor networks. Sensors 2010, 10, 2450–2459. [Google Scholar] [CrossRef] [PubMed]
- Vaidya, B.; Makrakis, D.; Mouftah, H.T. Improved two-factor user authentication in wireless sensor networks. In Proceedings of the IEEE 6th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Niagara Falls, ON, USA, 11–13 October 2010; pp. 600–606.
- Chen, T.H.; Shih, W.K. A Robust Mutual Authentication Protocol for Wireless Sensor Networks. ETRI J. 2010, 32, 704–712. [Google Scholar] [CrossRef]
- Fan, R.; Ping, L.D.; Fu, J.Q.; Pan, X.Z. A secure and efficient user authentication protocol for two-tiered wireless sensor networks. In Proceedings of the 2010 Second Pacific-Asia Conference on Circuits, Communications and System (PACCS), Beijing, China, 1–2 August 2010; Volume 1, pp. 425–428.
- Yeh, H.L.; Chen, T.H.; Liu, P.C.; Kim, T.H.; Wei, H.W. A secured authentication protocol for wireless sensor networks using elliptic curves cryptography. Sensors 2011, 11, 4767–4779. [Google Scholar] [CrossRef] [PubMed]
- Das, A.K.; Sharma, P.; Chatterjee, S.; Sing, J.K. A dynamic password-based user authentication scheme for hierarchical wireless sensor networks. J. Netw. Comput. Appl. 2012, 35, 1646–1656. [Google Scholar] [CrossRef]
- Xue, K.; Ma, C.; Hong, P.; Ding, R. A temporal-credential-based mutual authentication and key agreement scheme for wireless sensor networks. J. Netw. Comput. Appl. 2013, 36, 316–323. [Google Scholar] [CrossRef]
- Yuan, J.J. An enhanced two-factor user authentication in wireless sensor networks. Telecommun. Syst. 2014, 55, 105–113. [Google Scholar] [CrossRef]
- Turkanović, M.; Brumen, B.; Hölbl, M. A novel user authentication and key agreement scheme for heterogeneous ad hoc wireless sensor networks, based on the internet of things notion. Ad Hoc Netw. 2014, 20, 96–112. [Google Scholar]
- Farash, M.S.; Turkanović, M.; Kumari, S.; Hölbl, M. An efficient user authentication and key agreement scheme for heterogeneous wireless sensor network tailored for the Interne tof Things environment. Ad Hoc Netw. 2014, 36, 152–176. [Google Scholar] [CrossRef]
- Amin, R.; Islam, S.H.; Biswas, G.P.; Khan, M.K.; Leng, L.; Kumar, N. Design of an anonymity-preserving three-factor authenticated key exchange protocol for wireless sensor networks. Comput. Netw. 2016, 101, 42–62. [Google Scholar] [CrossRef]
- Kothmayr, T.; Schmitt, C.; Hu, W.; Brünig, M.; Carle, G. DTLS based security and two-way authentication for the Internet of Things. Ad. Hoc. Netw. 2013, 11, 2710–2723. [Google Scholar] [CrossRef]
- Schmitt, C.; Noack, M.; Stiller, B. Chapter 13: TinyTO: Two-way Authentication for Constrained Devices in the Internet-of-Things. In Internet-of-Things (Principles and Paradigms); Morgen Kaufmann: Cambridge, MA, USA, 2016; pp. 239–258. [Google Scholar]
- Porambage, P.; Schmitt, C.; Kumar, P.; Gurtov, A.; Ylianttila, M. Pauthkey: A pervasive authentication protocol and key establishment scheme for wireless sensor networks in distributed IoT applications. Int. J. Distrib. Sens. Netw. 2014, 2014. [Google Scholar] [CrossRef]
- Chen, L.; Wei, F.; Ma, C. A secure user authentication scheme against smart-card loss attack for wireless sensor networks using symmetric key techniques. Int. J. Distrib. Sens. Netw. 2015, 2015. [Google Scholar] [CrossRef]
- Kang, D.; Jung, J.; Mun, J.; Lee, D.; Choi, Y.; Won, D. Efficient and robust user authentication scheme that achieve user anonymity with a Markov chain. Secur. Commun. Netw. 2016, 9. [Google Scholar] [CrossRef]
- Syverson, P. A taxonomy of replay attacks [cryptographic protocols]. In Proceedings of the Computer Security Foundations Workshop VII, CSFW 7, Franconia, VA, USA, 14–16 June 2014; pp. 187–191.
- Chien-Ming, C.; Wei-Chi, K. Stolen-verifier attack on two new strong-password authentication protocols. IEICE Trans. Commun. 2002, 85, 2519–2521. [Google Scholar]
- Schultz, E.E. A framework for understanding and predicting insider attacks. Comput. Secur. 2002, 21, 526–531. [Google Scholar] [CrossRef]
- Wei-Chi, K.U.; Chang, S.T. Impersonation attack on a dynamic ID-based remote user authentication scheme using smart cards. IEICE Trans. Commun. 2005, 88, 2165–2167. [Google Scholar]
- Gong, L. Optimal authentification protocols resistant to password guessing attacks. In Proceedings of the IEEE 8th Computer Security Foundations Workshop, County Kerry, UK, 13–15 June 1995; pp. 24–29.
- Kim, J.; Lee, D.; Jeon, W.; Lee, Y.; Won, D. Security Analysis and Improvements of Two-Factor Mutual Authentication with Key Agreement in Wireless Sensor Networks. Sensors 2014, 14, 6443–6462. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.; Lee, D.; Kim, J.; Jung, J.; Nam, J.; Won, D. Security Enhanced User Authentication Protocol for Wireless Sensor Networks Using Elliptic Curves Cryptography. Sensors 2014, 14, 10081–10106. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.; Nam, J.; Lee, D.; Kim, J.; Jung, J.; Won, D. Security Enhanced Anonymous Multi-Server Authenticated Key Agreement Scheme Using Smart Cards and Biometrics. Sci. World J. 2014, 2014. [Google Scholar] [CrossRef] [PubMed]
- Kocher, P.; Jaffe, J.; Jun, B. Differential power analysis. In Proceedings of the Advances in Cryptology-CRYPTO’99, LNCS, Santa Barbara, CA, USA, 16 December 1999; Volume 1666, pp. 388–397.
- Amin, R.; Biswas, G.P. A secure light weight scheme for user authentication and key agreement in multi-gateway based wireless sensor networks. Ad Hoc Netw. 2016, 36, 58–80. [Google Scholar] [CrossRef]
- Li, X.; Niu, J.; Khan, M.K.; Liao, J. An enhanced smart card based remote user password authentication scheme. J. Netw. Comput. Appl. 2013, 36, 1365–1371. [Google Scholar] [CrossRef]
- Burrows, M.; Abadi, M.; Needham, R.M. A logic of authentication. Proc. R. Soc. Lond. A. Math. Phys. Sci. 1989, 426, 233–271. [Google Scholar] [CrossRef]
- Dai, W. Crypto++ Library, 5.6.1. Available online: http://www.cryptopp.com (accessed on 5 April 2011).
- Li, C.T.; Hwang, M.S.; Chu, Y.P. A secure and efficient communication scheme with authenticated key establishment and privacy preserving for vehicular ad hoc networks. Comput. Commun. 2008, 31, 2803–2814. [Google Scholar] [CrossRef]
- Li, C.T.; Weng, C.Y.; Lee, C.C. An advanced temporal credential-based security scheme with mutual authentication and key agreement for wireless sensor networks. Sensors 2013, 13, 9589–9603. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.C.; Le, H.D. A provably secure, efficient, and flexible authentication scheme for ad hoc wireless sensor networks. IEEE Trans. Wirel. Commun. 2015, 15, 357–366. [Google Scholar] [CrossRef]






| Value | Description |
|---|---|
| Remote user | |
| Sensor node | |
| Gateway node | |
| , | Identity and password of |
| Identity of | |
| Dynamic identity of | |
| k | The symmetric key |
| Encryption/Decryption with the symmetric key k | |
| The secret parameter generated by the , | |
| The shared key between the and | |
| The secret key instead of stored in , | |
| b | A random number chosen by |
| Cryptographic random numbers or nonces | |
| One-way hash function | |
| Concatenate operation | |
| ⊕ | XOR operation |
| ,,, | Current timestamp |
| Session key | |
| The maximum of transmission delay time |
| Features | Das et al. [13] | K-A- [14] | Vaidya et al. [15] | C-S- [16] | Fan et al. [17] | Yeh et al. [18] | Das et al. [19] | Xue et al. [20] | Chen et al. [28] | Proposed Scheme |
|---|---|---|---|---|---|---|---|---|---|---|
| Proposition 1 | × | √ | × | √ | √ | × | × | × | × | √ |
| Proposition 2 | √ | × | × | × | × | √ | √ | × | √ | √ |
| Proposition 3 | × | × | × | × | √ | √ | √ | √ | √ | √ |
| Proposition 4 | × | × | × | × | √ | × | √ | × | × | √ |
| Proposition 5 | × | √ | × | × | √ | × | × | × | √ | √ |
| Proposition 6 | × | × | × | × | × | × | × | × | √ | √ |
| Proposition 7 | √ | √ | √ | × | √ | √ | √ | √ | × | √ |
| Proposition 8 | √ | √ | √ | √ | √ | × | √ | √ | √ | √ |
| Proposition 9 | × | √ | √ | × | √ | √ | × | × | √ | √ |
| Proposition 10 | √ | × | √ | × | √ | √ | √ | √ | × | √ |
| Proposition 11 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| Proposition 12 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| Proposition 13 | × | √ | √ | × | × | × | √ | √ | √ | √ |
| Proposition 14 | × | × | √ | × | √ | √ | √ | √ | √ | √ |
| Schemes | User | Gateway Node | Sensor Node | Base Station | Total |
|---|---|---|---|---|---|
| Proposed scheme | - | ||||
| Chen et al. [28] | - | ||||
| Xue et al. [20] | - | ||||
| Das et al. [19] | - | ||||
| Yeh et al. [18] | - | ||||
| Fan et al. [17] | |||||
| C-S- [16] | - | ||||
| Vaidya et al. [15] | - | ||||
| K-A- [14] | - | ||||
| Das et al. [13] | - |
| Das’s [13] | K-A-’s [14] | Vaidya’s [15] | C-S-’s [16] | Fan’s [17] | Yeh’s [18] | Das’s [19] | Xue’s [20] | Chen’s [28] | Proposed Scheme |
|---|---|---|---|---|---|---|---|---|---|
| ≈0.0018 s | ≈0.0024 s | ≈0.0026 s | ≈0.002 s | ≈0.0038 s | ≈3.6016 s | ≈0.0542 s | ≈0.0052 s | ≈0.0368 s | ≈0.0374 s |
| Schemes | Total Number of Messages Required | Total Number of Bytes Required |
|---|---|---|
| Proposed scheme | 4 Messages | 216 Bytes |
| Chen et al. [28] | 4 Messages | 172 Bytes |
| Xue et al. [20] | 6 Messages | 284 Bytes |
| Das et al. [19] | 4 Messages | 253 Bytes |
| Yeh et al. [18] | 3 Messages | 118 Bytes |
| Fan et al. [17] | 3 Messages | 126 Bytes |
| Chen and Shih [16] | 4 Messages | 170 Bytes |
| Vaidya et al. [15] | 5 Messages | 157 Bytes |
| Khan and Alghathbar [14] | 4 Messages | 157 Bytes |
| Das et al. [13] | 3 Messages | 118 Bytes |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, J.; Kim, J.; Choi, Y.; Won, D. An Anonymous User Authentication and Key Agreement Scheme Based on a Symmetric Cryptosystem in Wireless Sensor Networks. Sensors 2016, 16, 1299. https://doi.org/10.3390/s16081299
Jung J, Kim J, Choi Y, Won D. An Anonymous User Authentication and Key Agreement Scheme Based on a Symmetric Cryptosystem in Wireless Sensor Networks. Sensors. 2016; 16(8):1299. https://doi.org/10.3390/s16081299
Chicago/Turabian StyleJung, Jaewook, Jiye Kim, Younsung Choi, and Dongho Won. 2016. "An Anonymous User Authentication and Key Agreement Scheme Based on a Symmetric Cryptosystem in Wireless Sensor Networks" Sensors 16, no. 8: 1299. https://doi.org/10.3390/s16081299
APA StyleJung, J., Kim, J., Choi, Y., & Won, D. (2016). An Anonymous User Authentication and Key Agreement Scheme Based on a Symmetric Cryptosystem in Wireless Sensor Networks. Sensors, 16(8), 1299. https://doi.org/10.3390/s16081299






