A High Precision Approach to Calibrate a Structured Light Vision Sensor in a Robot-Based Three-Dimensional Measurement System
Abstract
:1. Introduction
2. System Setup
- (1)
- Motoman-Hp6 robot;
- (2)
- Structured light vision sensor [9]; Its specifications are as follows: measuring accuracy is smaller than 0.06 mm; measuring range is (90 mm, 190 mm); sampling speed is 12,000 pts/s; measuring depth of field is 100 mm;
- (3)
- Master computer and measurement software system;
- (4)
- Robot controller;
3. Camera Model
4. Camera Calibration
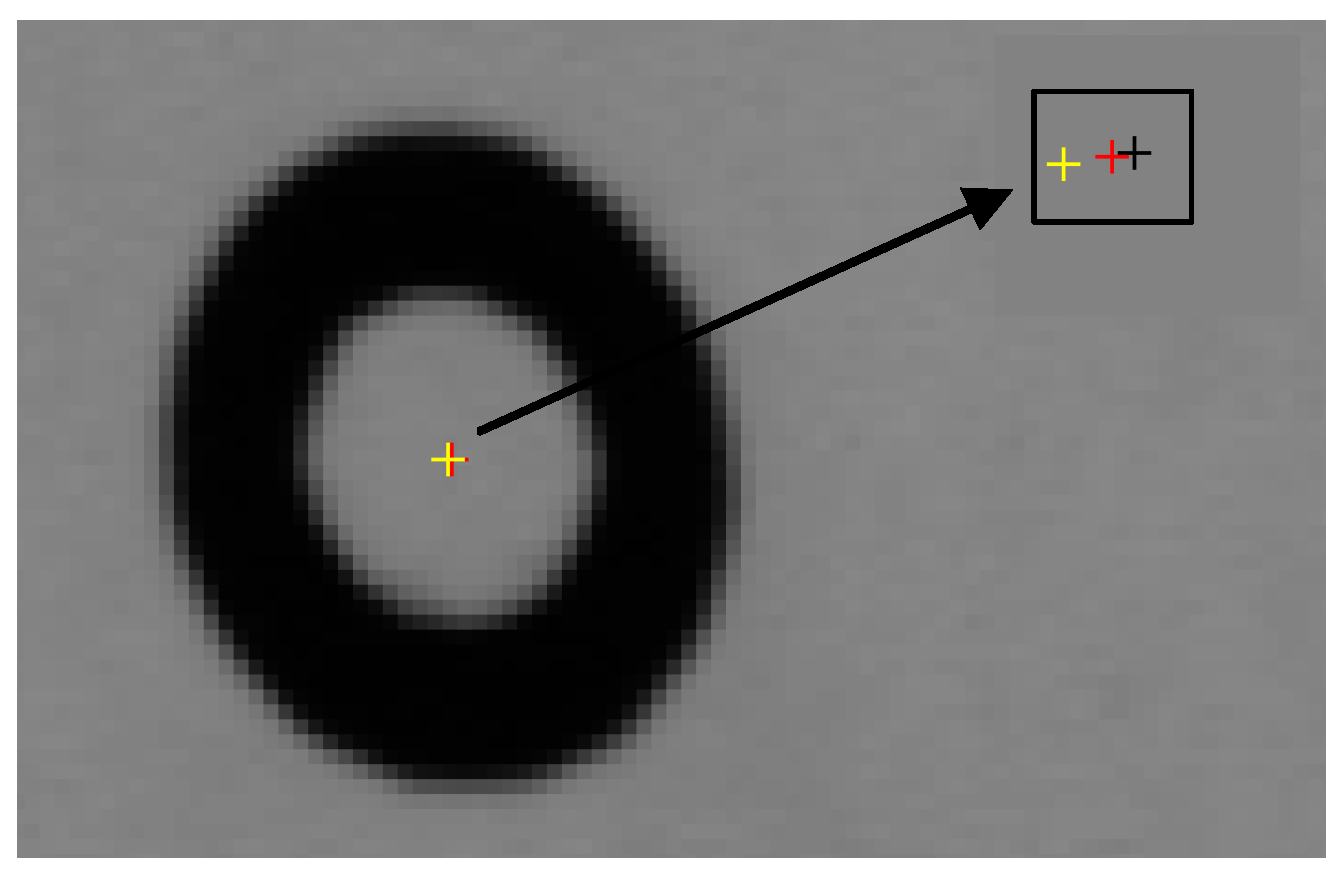
4.1. Extraction of the Calibration Points
Conclusion: The perspective projection of a concentric circle will produce two ellipses. A straight line will be obtained by the centres of the two ellipses, and the true concentric circle centre perspective projection is exactly on the line.
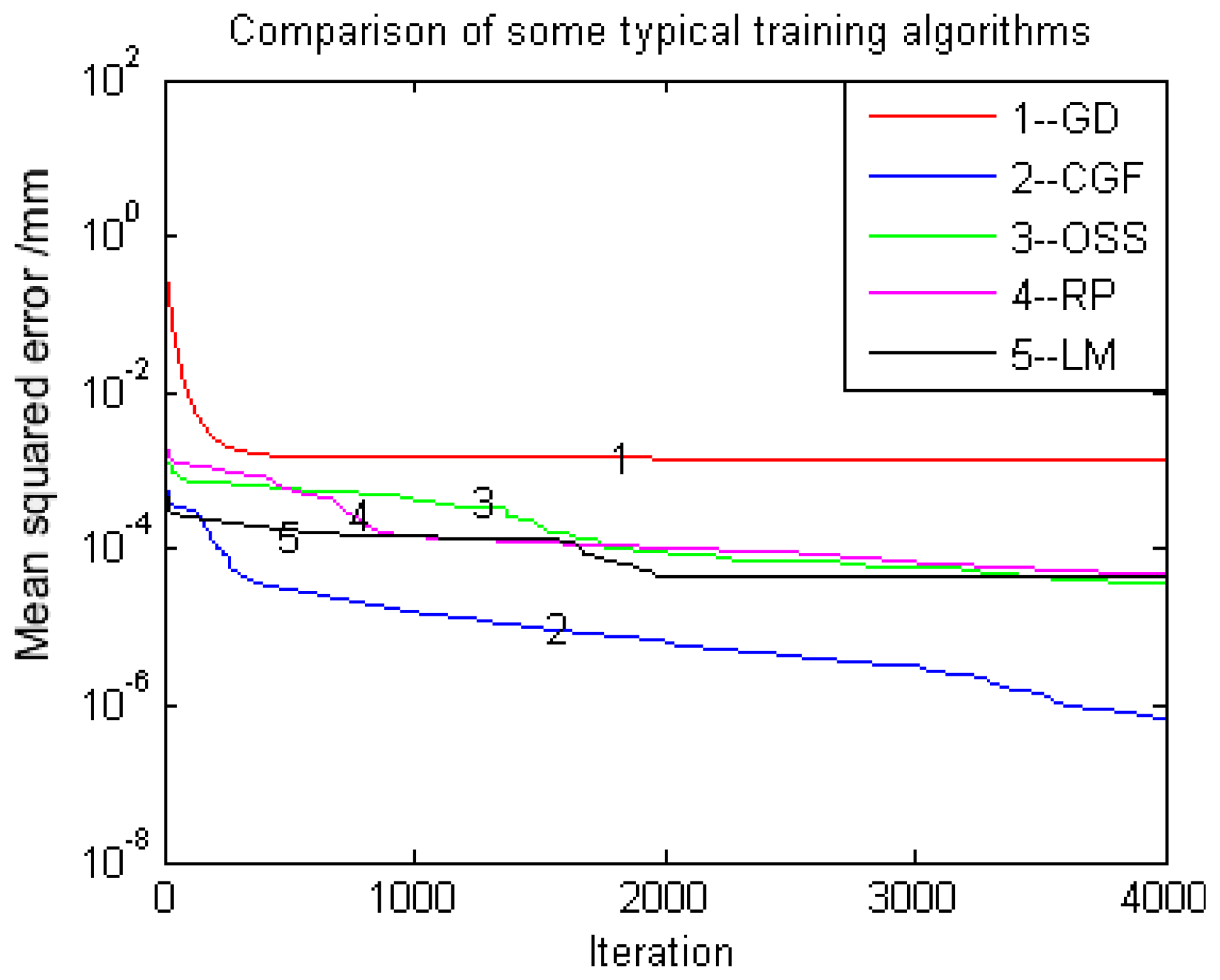
4.2. Solving Camera Model
4.3. Calibration Residuals Identification
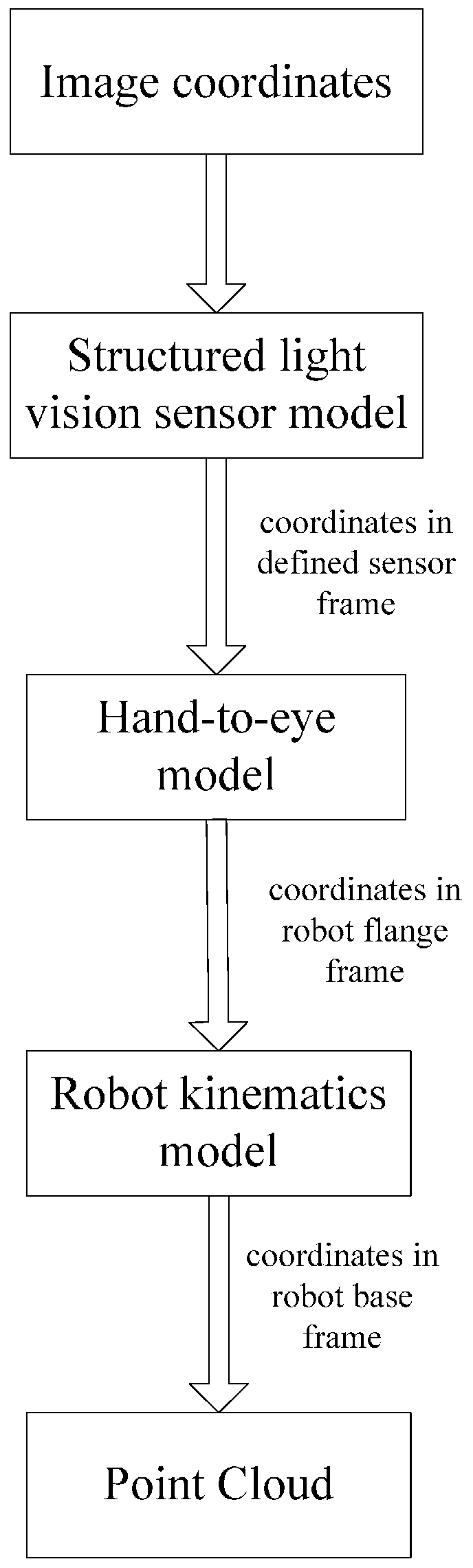
5. Calibration Point Generation Procedure
- Step 1:
- Make the robot end-effector move along its z axis when the robot is in its initial position. After the end-effector descends to a proper height, turn the laser on. Place the target on the fixed platform. The position of the target is chosen when the laser stripe covers the two auxiliary lines in the target, as depicted in Figure 10a.
- Step 2:
- Make the robot end-effector move along its z axis continuously. If the laser stripe does not cover the two auxiliary lines, as shown in Figure 10b, the robot must be rotated along its y axis. The laser stripe will be emitted to the target, as illustrated in Figure 10c. Control the robot to move along its x axis to make the laser stripe cover the auxiliary lines again, as shown in Figure 10d.
- Step 3:
- Repeat Step 2 until the laser stripe does not move away from the two auxiliary lines any more.
- Step 4:
- Shut down the laser and make the robot move along its z axis. The robot translation distance along the z axis, obtained through the robot controller, can be taken as the z coordinate in the calibration measurement coordinates. Its y coordinate can be obtained by the exact distance between the calibration points. The corresponding points in the image coordinates (u,v) are obtained via the described procedure given in Section 4, as shown in Figure 11. From the above procedure, the calibration points will be generated in the measuring range.
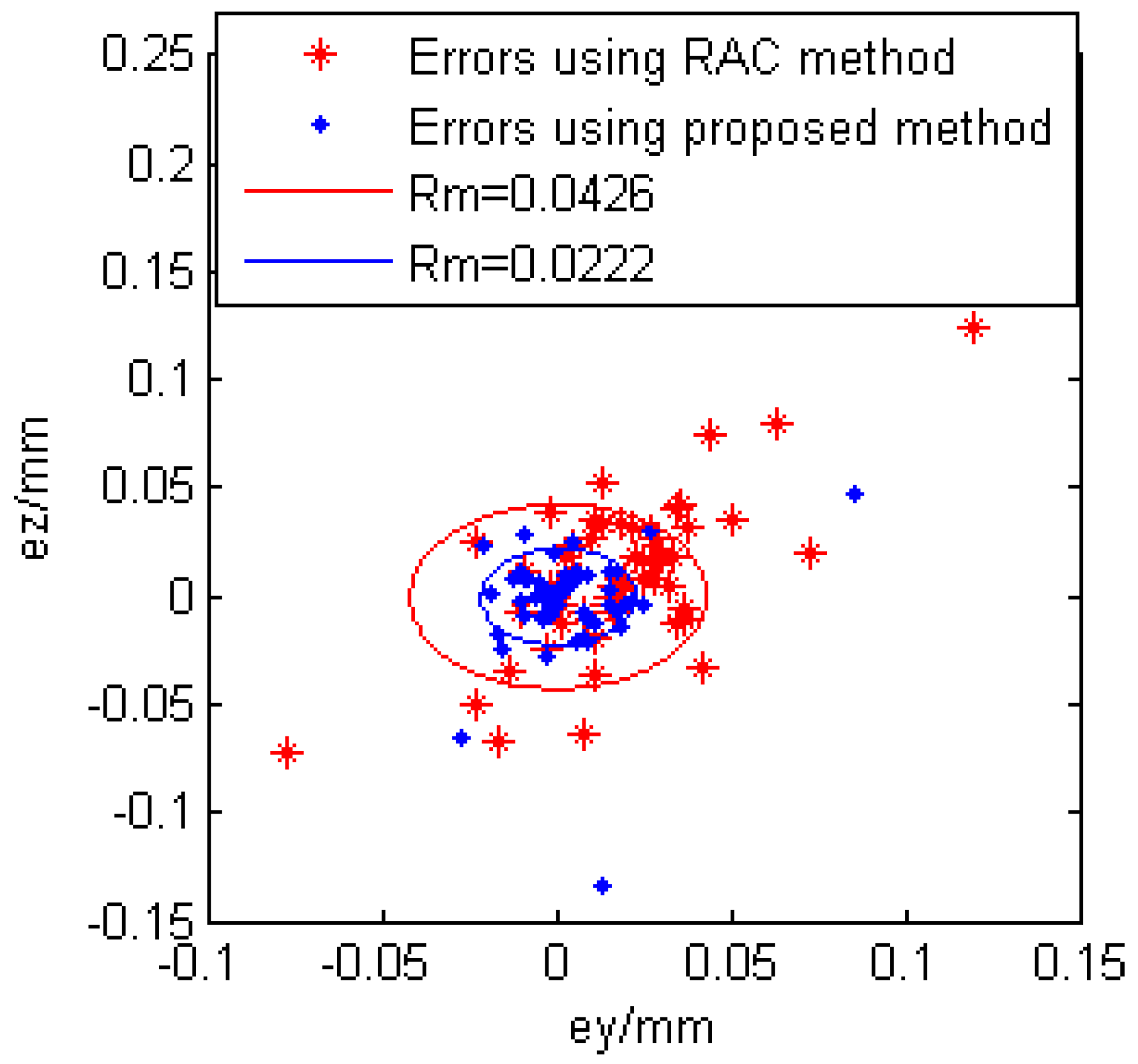
6. Expermental Results
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Portable 3D Scanners: Handyscan 3D. Available online: http://www.creaform3d.com/en/handyscan3d/products/default.aspx (accessed on 30 July 2016).
- 3D Software and Scanners. Available online: http://www.3dsystems.com/software-solutions (accessed on 30 July 2016).
- Li, R.J.; Fan, K.C.; Miao, J.W.; Huang, Q.X.; Tao, S.; Gong, E. An analogue contact probe using a compact 3d optical sensor for micro/nano coordinate measuring machines. Meas. Sci. Technol. 2014, 25, 1–33. [Google Scholar] [CrossRef]
- Jia, H.; Zhu, J.; Yi, W. Calibration for 3d profile measurement robot with laser line-scan sensor. Chin. J. Sens. Actuators 2012, 25, 62–66. [Google Scholar]
- Ma, Z.; Xu, H.; Hu, Y.; Wu, D.; Zhu, Q.M.; Chen, M. A Novel Robot Surface Measurement System Enhanced with 3D Surface Reconstruction. Int. J. Model. Identif. Control 2008, 4, 288–298. [Google Scholar] [CrossRef]
- Larsson, S.; Kjellander, J. Motion control and data capturing for laser scanning with an industrial robot. Robot. Auton. Syst. 2006, 54, 453–460. [Google Scholar] [CrossRef]
- Li, J.; Zhu, J.; Guo, Y.; Lin, X.; Duan, K.; Wang, Y.; Tang, Q. Calibration of a Portable laser 3D Scanner used by a robot and its use in measurement. Opt. Eng. 2008, 47, 017202. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.F.; Wang, Q.L.; Xu, D.; Tan, M. Measurement and Defect Detection of the Weld Bead Based on Online Vision Inspection. IEEE Trans. Instrum. Meas. 2010, 59, 1841–1849. [Google Scholar]
- Zhao, J.; Ma, Z.; Zhu, Q.M.; Lin, N. A novel adaptive laser scanning sensor for reverse engineering measurement. Chin. J. Sci. Instrum. 2007, 28, 1164–1169. [Google Scholar]
- Zhao, Y.; Xiaodan, L.V.; Wang, A. A Nonlinear Camera Self-calibration Approach based on Active Vision. J. JDCTA 2011, 5, 34–42. [Google Scholar]
- Sun, Q.; Wang, X.; Xu, J.; Wang, L.; Zhang, H.; Yu, J.; Su, T.; Zhang, X. Camera self-calibration with lens distortion. Optik Int. J. Light Electron Opt. 2016, 127, 4506–4513. [Google Scholar] [CrossRef]
- Zhao, B.; Hu, Z. Camera self-calibration from translation by referring to a known camera. Appl. Opt. 2015, 54, 7789–7798. [Google Scholar] [CrossRef] [PubMed]
- Maybank, S.J.; Faugeras, O.D. A theory of self-calibration of a moving camera. Int. J. Comput. Vis. 1992, 8, 123–151. [Google Scholar] [CrossRef]
- Zhang, Z. Camera Calibration. In Emergin Topics in Computer Vision; Medioni, G., Kang, S.B., Eds.; Prentice Hall Professional Technical Reference: Upper Saddle River, NJ, USA, 2004; pp. 4–43. [Google Scholar]
- Faugeras, O. Three-Dimensional Computer Vision: A Geometric Viewpoint; MIT Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Grammatikopoulos, L.; Karras, G.E.; Petsa, E. Camera Calibration Approaches Using Single Images of Man-Made Objects. In Proceedings of the CIPA 2003 XIXth International Symposium, Antalya, Turkey, 30 September–4 October 2003.
- Guan, T.; Duan, L.Y.; Yu, J.Q. Real-time camera pose estimation for wide-area augmented reality applications. IEEE Comput. Graph. Appl. 2011, 31, 56–68. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.Y. Flexible Camera Calibration by Viewing a Plane from Unknown Orientations. In Proceedings of the 7th IEEE conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; pp. 666–673.
- Zhang, Z. Camera calibration with one-dimensional objects. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 892–899. [Google Scholar] [CrossRef] [PubMed]
- Peng, E.; Li, L. Camera calibration using one-dimensional information and its applications in both controlled and uncontrolled environments. Pattern Recognit. 2010, 43, 1188–1198. [Google Scholar] [CrossRef]
- Deng, X.; Wu, F.; Wu, Y.; Chang, L. Calibration of central catadioptric camera with one-dimensional object undertaking general motions. IEEE Int. Conf. Image Process. 2011, 6626, 637–640. [Google Scholar]
- Qiang, F.U.; Quan, Q.; Cai, K.Y. Calibration method and experiments of multi-camera’s parameters based on freely moving one-dimensional calibration object. Control Theory Appl. 2014, 31, 1018–1024. [Google Scholar]
- Heikkilä, J. Geometric camera calibration using circular control points. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1066–1077. [Google Scholar] [CrossRef]
- Kim, J.; Kim, H.; Kweon, I.S. A Camera Calibration Method Using Concentric Circles for Vision Applications. In Proceedings of the 5th Asian Conference on Computer Vision, Melbourne, Australia, 23–25 January 2002; pp. 515–520.
- Xing, D.; Da, F.; Zhang, H. Research and application of locating of circular target with high accuracy. Chin. J. Sci. Instrum. 2009, 30, 2593–2598. [Google Scholar]
- Tsai, R.Y. A versatile camera calibration technique for high accuracy 3D machine vision metrology using off-shelf TV camera and lenses. IEEE J. Robot. Autom. 1987, 3, 323–334. [Google Scholar] [CrossRef]
- Weng, J.; Cohen, P.; Herniou, M. Camera Calibration with Distortion Models and Accuracy Evaluation. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 965–980. [Google Scholar] [CrossRef]
- Salvi, J.; Armangué, X.; Batlle, J. A comparative review of camera calibrating methods. Pattern Recognit. 2002, 35, 1617–1635. [Google Scholar] [CrossRef]
- Fitzgibbon, A.W. Simultaneous linear estimation of multiple view geometry and lens distortion. In Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, Kauai, HI, USA, 8–14 December 2001; pp. 125–132.
- Wang, A.; Qiu, T.; Shao, L. A simple method of radial distortion correction with centre of distortion estimation. J. Math. Imaging Vis. 2009, 35, 165–172. [Google Scholar] [CrossRef]
- Chen, T.; Zhao, J.; Wu, X. New calibration method for line structured light sensor based on planar target. Acta Opt. Sin. 2015, 35, 180–188. [Google Scholar]
- Wei, Z.; Shao, M.; Zhang, G.; Wang, Y. Parallel-based calibration method for line-structured light vision sensor. Opt. Eng. 2014, 53, 1709–1717. [Google Scholar] [CrossRef]
- Liu, Z.; Li, X.; Li, F.; Zhang, G. Calibration method for line-structured light vision sensor based on a single ball target. Opt. Lasers Eng. 2015, 69, 20–28. [Google Scholar] [CrossRef]
- Liu, Z.; Li, X.; Yin, Y. On-site calibration of line-structured light vision sensor in complex light environments. Opt. Express 2015, 23, 29896–29911. [Google Scholar] [CrossRef] [PubMed]
- Xie, Z.; Zhu, W.; Zhang, Z.; Jin, M. A novel approach for the field calibration of line structured-light sensors. Measurement 2010, 43, 190–196. [Google Scholar]
- Zhang, G.; Wei, Z. A novel calibration approach to structured light 3D vision inspection. Opt. Laser Technol. 2002, 34, 373–380. [Google Scholar] [CrossRef]
- Mestre, G.; Ruano, A.; Duarte, H.; Silva, S.; Khosravani, H.; Pesteh, S.; Ferreira, P.M.; Horta, R. An Intelligent Weather Station. Sensors 2015, 15, 31005–31022. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; Ma, Z.; Wu, D. Hand-to-eye calibration for 3D surface digitalization system. Int. J. Model. Identif. Control 2009, 6, 263–269. [Google Scholar] [CrossRef]
- Da, F.; Zhang, H. Sub-pixel edge detection based on an improved moment. Image Vis. Comput. 2010, 28, 1645–1658. [Google Scholar] [CrossRef]














| Coordinate of Principal Point (u0,v0) | Scale Factor sx | Focal Length f (mm) | Radial Distortion Coefficient k (pixel−2) | Rotation Matrix R | Transformation Matrix T |
|---|---|---|---|---|---|
| 387, 305 | 0.96 | 11.6401 | −0.0012 |
| No. | u (pixel) | v (pixel) | y (mm) | z (mm) | RAC Method | Proposed Method | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| y’ (mm) | z’ (mm) | e (mm) | y’ (mm) | z’ (mm) | e (mm) | |||||
| 1 | 342.2818 | 137.1483 | 10 | 9 | 9.9836 | 9.0386 | 0.0419 | 9.9754 | 9.0144 | 0.0285 |
| 2 | 345.6897 | 198.8738 | 5 | 9 | 4.9487 | 9.0155 | 0.0536 | 4.9317 | 8.9999 | 0.0683 |
| 3 | 349.1362 | 260.2563 | 0 | 9 | −0.0299 | 8.9886 | 0.0320 | 0.0148 | 9.0079 | 0.0168 |
| 4 | 352.6949 | 322.7341 | −5 | 9 | −5.0806 | 8.9584 | 0.0907 | −5.0466 | 8.9397 | 0.0762 |
| 5 | 355.3254 | 383.8221 | −10 | 9 | −10.0125 | 9.0492 | 0.0507 | −9.9765 | 9.0169 | 0.0290 |
| 6 | 358.8092 | 446.0491 | −15 | 9 | −15.0493 | 9.0354 | 0.0606 | −14.9817 | 9.0136 | 0.0229 |
| Ave. | 0.0549 | 0.0403 | ||||||||
| No. | Radius Measured by Vision Sensor after RAC Calibration/mm | Radius Measured by Vision Sensor after the Proposed Calibration Method/mm |
|---|---|---|
| 1 | 14.3446 | 14.2864 |
| 2 | 14.3586 | 14.3008 |
| 3 | 14.3517 | 14.3199 |
| 4 | 14.3539 | 14.3123 |
| 5 | 14.3502 | 14.3476 |
| 6 | 14.3173 | 14.3127 |
| 7 | 14.3180 | 14.3219 |
| 8 | 14.3182 | 14.3250 |
| 9 | 14.3292 | 14.3331 |
| 10 | 14.3263 | 14.3461 |
| Average | 14.3368 | 14.3206 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, D.; Chen, T.; Li, A. A High Precision Approach to Calibrate a Structured Light Vision Sensor in a Robot-Based Three-Dimensional Measurement System. Sensors 2016, 16, 1388. https://doi.org/10.3390/s16091388
Wu D, Chen T, Li A. A High Precision Approach to Calibrate a Structured Light Vision Sensor in a Robot-Based Three-Dimensional Measurement System. Sensors. 2016; 16(9):1388. https://doi.org/10.3390/s16091388
Chicago/Turabian StyleWu, Defeng, Tianfei Chen, and Aiguo Li. 2016. "A High Precision Approach to Calibrate a Structured Light Vision Sensor in a Robot-Based Three-Dimensional Measurement System" Sensors 16, no. 9: 1388. https://doi.org/10.3390/s16091388
APA StyleWu, D., Chen, T., & Li, A. (2016). A High Precision Approach to Calibrate a Structured Light Vision Sensor in a Robot-Based Three-Dimensional Measurement System. Sensors, 16(9), 1388. https://doi.org/10.3390/s16091388





