Abstract
With the rapid growth of the health data scale, the limited storage and computation resources of wireless body area sensor networks (WBANs) is becoming a barrier to their development. Therefore, outsourcing the encrypted health data to the cloud has been an appealing strategy. However, date aggregation will become difficult. Some recently-proposed schemes try to address this problem. However, there are still some functions and privacy issues that are not discussed. In this paper, we propose a privacy-enhanced and multifunctional health data aggregation scheme (PMHA-DP) under differential privacy. Specifically, we achieve a new aggregation function, weighted average (WAAS), and design a privacy-enhanced aggregation scheme (PAAS) to protect the aggregated data from cloud servers. Besides, a histogram aggregation scheme with high accuracy is proposed. PMHA-DP supports fault tolerance while preserving data privacy. The performance evaluation shows that the proposal leads to less communication overhead than the existing one.
1. Introduction
Recently, many information techniques have been utilized for healthcare systems [1] to reduce the expenses and boost the efficiency of medical services. Specifically, the application of wireless body area networks (WBANs) [2] is a promising technique, which has a huge potential to revolutionize the future of healthcare monitoring by diagnosing many life-threatening diseases and providing real-time patient monitoring [3]. WBANs can continuously monitor patient’s physiological attributes, such as blood pressure, body temperature, electrocardiograph (ECG), electroencephalogram (EEG) [4], and so on. Usually, all of the detected data are gathered by the user’s personal digital assistant (PDA) or smartphone. Hence, aggregating and analyzing this sensitive health information is crucial for medical institutions.
In the era of big data, health data aggregation is the basic work of medical big data analysis. Actually, both spatial and temporal aggregation services are widely applied in many healthcare scenarios. For instance, in an elderly community, there are some patients who suffer from hypertension. All of these patients may be equipped with body area sensors to monitor their blood pressure. The collected data of each patient are uploaded to the authorized hospital via smart devices. Therefore, the hospital can obtain each user’s maximum/minimum blood pressure over the past day. If one patient’s blood pressure is abnormal, the doctor may ask the patient to come to the hospital to have a further treatment. It is a typical temporal aggregation [5] case, which helps hospital provide better healthcare service. For a medicine research center and health bureau, the spatial aggregate statistics [6] (e.g., the average blood pressure of users in a specific community) may be much more useful than temporal aggregation.
However, with the rapidly increasing amount of health information, the cost of providing e-health services is becoming high for some hospitals and medical research institutions. In addition, the traditional WBANs have limited computation and storage resources, which have difficulty satisfying the needs of practical applications. Therefore, outsourcing large-scale health data to the cloud is a cost-efficient choice to release the burdens of data storage and data management. Therefore, in this paper, we leverage the cloud-assisted WBANs to accomplish the mission of storing and processing health data. Unfortunately, the original system model of cloud computing may suffer from the problems of data security and user privacy. Because the cloud server is honest-but-curious, it may reveal the content of personal health information. For instance, a patient’s living and eating habits can be reflected by his or her ECG. Thus, the health data should be protected from malicious entities. A direct solution to preserve the privacy and integrity of health data is to let the data owners encrypt them before outsourcing. However, conventional encryption schemes make data aggregation computation harder to run. Thus, many privacy-preserving schemes are proposed to address this problem, such as [7,8,9]. However, these schemes only calculate summation aggregation or additive aggregation [10]. Recently, Han et al. [6] proposed a scheme to achieve additive and non-additive aggregation simultaneously. However, some functions are still not discussed, such as the weighted average. Besides, the histogram aggregation is also not investigated thoroughly in [6]. Furthermore, the sum of all of the users’ health data may be disclosed by cloud servers in Han et al.’s scheme [6].
In this paper, to address the above problems, we propose a privacy-enhanced and multifunctional health data aggregation scheme under differential privacy guarantees (PMHA-DP). Specifically, the main contributions of this paper can be summarized as follows:
- First, we propose a basic average aggregation scheme (BAAS) by utilizing the Boneh–Goh–Nissim cryptosystem. Note that, in some scenarios, the data analysts would prefer to acquire the weighted average; because, the weighted average can be more objective to reflect the overall state of all users. Thus, we propose a privacy-preserving weighted average scheme (WAAS) to meet the above requirement. To the best of our knowledge, this paper is the first to discuss the weighted average aggregation. Besides, the final results of both schemes are protected by differential privacy mechanisms [11].
- Second, we provide a privacy-enhanced average aggregation scheme (PAAS) to protect the sum of all of the gathered health data. In [6], one of the working cloud servers is able to obtain the plaintext of the sum. If this server is compromised, it may leak the information to some malicious entities. Therefore, we design a protocol with additional private keys to hide the aggregated data. PAAS hides the sum of the dataset from the cloud servers. It further protects the users’ privacy.
- Third, histogram aggregation is well studied in this paper. We leverage the hierarchical method [12] for histogram (HMH). Then, we add Laplace noise [13] to the query result. Moreover, we also leverage the post-processing technique [12] to boost the accuracy of the released answer.
- Finally, we conduct real experiments and compare PMHA-DP with the other scheme [6]. The comparison results show that our non-additive aggregation scheme (NAS) and PAAS lead to less communication overhead than that of another scheme called [6]. Besides, PAAS enhances the data privacy with acceptable computational overhead. Moreover, we give a security analysis to show that the proposed scheme preserves data privacy under the given strong adversary model. More importantly, all of the proposed aggregation protocols support fault tolerance.
The remainder of this paper is organized as follows. In Section 2, the system model of PMHA-DP, the adversary model and the security requirements are formalized. We recall the Boneh–Goh–Nissim cryptosystem and differential privacy in Section 3. In Section 4, we propose our scheme. This is followed by the security, privacy analysis and performance evaluation in Section 5 and Section 6, respectively. In Section 7, we give some further discussions on four vital topics. The related work is introduced in Section 8. Finally, we conclude this paper in Section 9.
2. Problem Statement
In this section, we will introduce the system model, adversary model, security and privacy requirements of PMHA-DP to formalize the research problems.
2.1. System Model
As shown in Figure 1, the system model of PMHA-DP is composed of four entities: mobile users, cloud servers, trusted authority and healthcare institutions. Each entity is introduced as follows.
- Mobile users (MUs): MUs are the data providers of the cloud-assisted WBAN system, which are denoted as . Specifically, is equipped with some body area sensors to monitor different types of health data. Then, the original health data collected by sensors will be stored in ’s smartphone or PDA. For privacy consideration, MUs encrypt the data using the smartphone before reporting them to the cloud servers. Furthermore, MUs report the personal health data according to the aggregation protocols formulated by the trusted authority.
- Cloud servers (CSs): CSs are a group of public cloud servers denoted as . In PMHA-DP, multiple servers are necessary for executing the aggregation missions and supporting fault tolerance. A large volume of health data is stored in CSs. The aggregation result will be delivered to the trusted authority instead of healthcare institutions directly. According to the practice, we assume that all of the CSs are honest-but-curious. CSs store and process data honestly, but they may be also curious about individual user’s health data. Thus, CSs only store the ciphertexts of health data received from MUs. Since CSs are powerful, we assume that a strong adversary can compromise or paralyze no more than cloud servers.
- Trusted authority (TA): TA is a powerful data center, which is responsible for assigning aggregation tasks and key management. TA receives different aggregation requests from healthcare institutions, then it bootstraps the whole system. In the initialization phase, TA first generates secret keys and US certificates for each registered user. Besides, keys and certificates are distributed through a secure channel. Meanwhile, TA also generates private keys for cloud servers. If TA wants some statistical information of the health dataset, it will make cloud servers work together to aggregate and decrypt the data. Then, the system randomly selects one of the working cloud servers to send the statistics to TA. At last, TA will calculate the final result and adds noise to it by utilizing differential privacy mechanisms. TA is the only globally-trusted entity of the whole system.
- Healthcare institutions (HIs): HIs represent the organizations (i.e., certified hospital, medicine research center, health departments, etc.) that are interested in the statistical information of a large volume of health data. HIs obtain this information by sending specific requests to TA, and TA returns the final result to HIs.
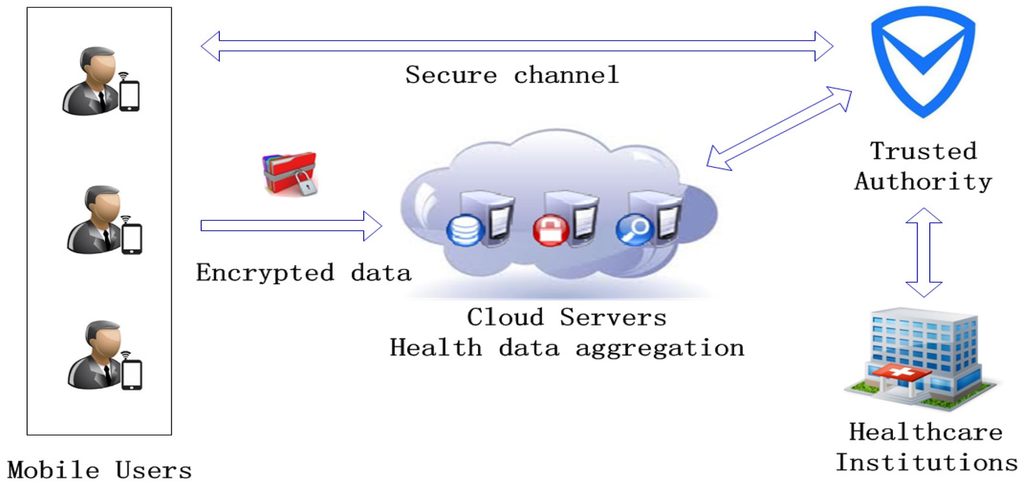
Figure 1.
System model of privacy-enhanced and multifunctional health data aggregation scheme (PMHA-DP).
In order to convince us that the system model is practical, we make a further discussion. Differential private techniques are firstly designed to resist the differential attacks. As the development of differential privacy, data sanitizing schemes are proposed. Those schemes add a little bit of noise to the users’ local data to protect the sensitive information. However, those techniques cannot hide all of the personal information. For instance, a user adds a little noise to his/her body temperature (suppose the original value is 37). The noisy value may be quite close to the original value, such as 37.5. If the data are not encrypted, the public cloud can deduce the distribution and some other statistical information of the dataset. The mathematical expectation of the permutated dataset is the same as the original dataset. Therefore, the cloud server can infer that the dataset must be the users’ temperatures if the mathematical expectation is about 37. Since the ciphertext contains no statistical information, all of that sensitive information can be protected against the public cloud if all users’ data are encrypted. In order to resist differential attack, we add noises to the final aggregation results instead of encrypting the data (again) and sending the encrypted data to HI. If we choose to encrypt the results again without permutation, HI can deduce some individual records’ by asking legitimate queries. Thus, it is necessary to release the result under differential privacy.
2.2. Adversary Model
In PMHA-DP, a strong adversary is considered. may launch the following attacks:
- may eavesdrop on communication flows.
- may compromise some users directly.
- may compromise less than CSs to breach users’ privacy.
- In our privacy-enhanced health data aggregation scheme, may compromise all of the working cloud servers and obtain the sum of all users’ private data.
- may launch differential attacks on TA (e.g., may deduce the newly-added users’ data by asking TA legitimate queries).
2.3. Security and Privacy Requirements
The adversary would like to reveal as much of the users’ personal private information as possible. Therefore, the designed data aggregation system should resist ’s attacks. Specifically, the scheme must satisfy the following security and privacy requirements:
- cannot reveal users’ private health data, even if the communication flows are intercepted.
- cannot reveal the uncompromised users’ private health data, even if some users are compromised directly.
- cannot reveal users’ private health data, even if l cloud servers are compromised.
- cannot obtain the sum of all of the users’ private data, even if all of the working cloud servers are compromised.
- cannot deduce any individual user’s health data by launching differential attacks on TA.
3. Preliminaries
In this section, we will briefly present the concept of differential privacy and the cryptographic building block that PMHA-DP builds on. At last, we give a further discussion on the data type and differential privacy mechanism.
3.1. Boneh–Goh–Nissim Cryptosystem
Boneh et al. [14] presented a homomorphic public key encryption scheme based on finite groups of composite order that support a bilinear map. Their system supports arbitrary additions and one multiplication on encrypted data. Due to those homomorphic features, it is often used to achieve privacy-preserving data aggregation tasks. Here, we introduce the three algorithms making up the system.
- Given a security parameter , the system runs to acquire a tuple . Here, and are two cyclic groups of order . In addition, is a bilinear map [15]. Randomly pick two generators , and set . Then, h is a random generator of the subgroup of of order p. The public key is . The private key is .
- Let represent a message, and T is the upper bound of the message space. To encrypt a message m using public key , the user picks a random number r and calculates the ciphertext as .
- The system decrypts ciphertext C with private key through computing . Let . Then, the system computes the discrete logarithm of base to recover m. The computation takes the expected time using Pollard’s lambda method [16].
Here, we introduce the two homomorphic properties of the Boneh–Goh–Nissim cryptosystem.
- Firstly, the system is clearly additively homomorphic. Given any two ciphertexts of messages , respectively, one can obtain the encryption of by computing the product .
- Secondly, one can multiply two encrypted messages once using the bilinear map to acquire the product of two messages. Let , , and set where is unknown. Suppose that the two given ciphertexts are and . Then, we have:where , and . Thus, C is the ciphertext of , and the recovery of is similar to . Furthermore, the system is still additively homomorphic in .
3.2. Differential Privacy
Differential privacy [11] was first proposed by Dwork. Informally, if an algorithm is not sensitive to small changes in the input, then it may be differentially private. The idea of a differential privacy protection model is derived from a very simple observation: when the dataset D contains individual Alice, let f be arbitrary query operation on D (such as count, sum, average, median or other range queries, etc.); the results obtained are . If the result of the query is still when Alice’s record is deleted, you can indicate that Alice’s privacy is protected from the differential attack. Differential privacy is to ensure that any operation on a single record (e.g., add, remove or change a record) cannot impact the final result of the query. In other words, there are two almost identical sets of data (only one record is different); the probability of getting the same result from the same query that is operated on the two datasets is close to one.
Formally, for any given database instance D, let denote the set of neighboring databases differing from D by at most one record; i.e., if , then . Let function be the output range of the random algorithm . Then, the formal definition is shown below.
Definition 1.
An randomized algorithm is ϵ-differentially private if for all instances D, any , and any subset of outputs , the following holds:
where ϵ is the privacy budget.
Different from the encryption-based schemes, differential privacy does not have a security level (e.g., secure under chosen plaintext attack, etc.). The privacy level of the differential private algorithm depends on the privacy budget ϵ. It is set by the user; the larger the privacy budget is, the smaller the noise is. Thus, the privacy budget is inversely proportional to the accuracy of the query result.
In this paper, we adopt the Laplace mechanism [13] to design differential privacy algorithms. The Laplace mechanism utilizes the sensitivity of the query function to calibrate the noise scale. The definition of the function sensitivity is shown as below.
Definition 2.
Given a function , the sensitivity of f, denoted , is:
Let denote the Laplace probability distribution with mean zero and scale λ. The Laplace mechanism achieves differential privacy by adding Laplace noise to the output of function f.
Definition 3.
Let f be an aggregation function of a database D and be a random variable where . The Laplace mechanism is defined as:
The randomized algorithm is ϵ-differentially private.
The data type in this paper is numerical. We cannot calculate the statistics of the categorical data under the ciphertext environment. For instance, there exists an attribute recording the favorite sports of the user. In the database, we can use integral numbers to represent the categorical data (e.g., one represents ąřfootballąś, two represents ąřbasketballąś, etc.). However, it is meaningless to calculate the average or summation of the categorical data. Since the aggregation tasks can be assigned to the cloud in any time, the cloud servers and the data should be online. The encrypted data are stored in relational tables. However, the attribute types and the record values are all encrypted or permutated. There is no limit to the size of the data. The user could encrypt some short health message, such as blood pressure, temperature, and so on. Therefore, the expected maximum value of those health data depends on the observation of clinical medicine. For example, a person’s blood pressure is usually less than 140 mmHg. Then, we can use this value to quantify the sensitivity of aggregation functions.
Interactive and non-interactive differential privacy mechanisms are significantly different. The interactive mechanism allows the user to query several times until the privacy budget is consumed. The non-interactive mechanism answers all of the queries at one time. The Laplace mechanism applied in this paper is interactive. Therefore, the proposed differential privacy scheme is interactive.
4. Proposed Scheme
In this section, we propose a multifunctional health data additive aggregation scheme and a non-additive aggregation scheme, respectively. “Multifunctional” means that we provide different aggregation functions. It is an important property that reflects the scalability and the practicability of a data aggregation scheme. Our scheme achieves the average, the summation, the median and some other aggregation functions simultaneously. In the first part, we only illustrate the average aggregation as an example of additive aggregation. In the second part, we will discuss various non-additive aggregations, such as min/max, median, histogram, etc., which are widely applied in reality. Furthermore, advanced schemes are also proposed.
4.1. Additive Aggregation of Health Data
In this part, we will show the details of the basic average aggregation and weighted average aggregation scheme. Besides, the final results calculated by TA strictly satisfy the differential privacy. Compared with the scheme proposed by Han et al. [6], PMHA-DP is well designed with less noise being added, which improves the accuracy of the final results significantly. In [6], the cloud servers are able to decrypt and learn the sum of health data. However, the statistical information (i.e., sum of the dataset) may be sensitive and should not be disclosed to the public. On addressing the above problem, we propose a new advanced average aggregation protocol.
4.1.1. System Initialization
In the phase of initialization, TA bootstraps the system and generates public and private keys. Firstly, TA runs to obtain a bilinear map tuple . As previously stated in Section 3.1, TA generates the tuple by leveraging the Boneh–Goh–Nissim cryptosystem. is a random generator of the subgroup of of order p, and is a random generator of . In addition, TA chooses a one-way hash function . Hence, the public key is , and the private key is p. Moreover, the private key is seen as a shared secret, and each share of p is assigned to each working cloud server. For simplicity, TA utilizes Shamir’s [17] secret share scheme. TA first randomly generates a polynomial function , then TA calculates as ’s private key, where .
4.1.2. Basic Average Aggregation Scheme
Since we can easily calculate the average of the dataset from its sum, the working CSs firstly compute the sum and deliver it to TA. Then, TA computes the average of dataset. Details are shown as follows.
User generates ciphertext: Mobile user’ health data are detected by body sensors, and the original data are all stored and processed in the user’s smartphone or PDA. The detected data directly reflects the health status of users. Thus, MUs would like to report their health data to the healthcare institutions and acquire health services. However, the health data may leak some sensitive information of individuals. Consequently, users encrypt their data before submitting them to the public cloud. Specifically, each user encrypts his or her health data at time point through the following three steps:
- Step 1: computes the hash value at the time point .
- Step 2: encrypts the message through calculating , where is a random number.
- Step 3: submits the ciphertext to one of the working cloud servers.
Privacy-preserving computing of : One of the working cloud servers receives all of the users’ encrypted health data of message set . According to the privacy requirements, the cloud server needs to compute the encrypted sum without knowing the plaintext of any specific message. By utilizing the homomorphic property of Boneh–Goh–Nissim, we can obtain the encrypted aggregation as follows:
where .
Joint decryption of : Before each aggregation task begins, TA randomly chooses cloud servers as the working servers. As mentioned above, one of the cloud severs calculates and sends it to the other l working cloud servers. Upon receiving at time point , each cloud server first calculates:
then computes:
Then, TA selects one of the servers to gather all of the computed by each and calculates:
where . According to the Lagrange interpolation polynomial [17], we have:
Thus,
Since , we have . The CS can obtain the sum of users’ health data , by computing the discrete logarithm of based on in expected time . At last, the CS sends to TA.
Result release under differential privacy: Different from scheme proposed in [6], CS cannot release any data to the analyst directly. CS must send the intermediate result to TA first. TA is responsible for computing the final result and releasing it under differential privacy. The details of the computation and proof of differential privacy are shown as follows.
Once TA receives the sum of dataset , TA can get the average value by simply calculating . In order to ensure differential privacy, we add noise to M by leveraging the Laplace mechanism. Let be a random variable, and . Here, is the Laplace noise, which will be added to M. Then, TA simply computes . Finally, is returned to the data analyst (HIs) as the final result. We can assert that the released result is ϵ-differentially private. The mainly challenge is the proof of the differential privacy. The formal proof of differential privacy is given in Section 5.
4.1.3. Weighted Average Aggregation Scheme
In a real data aggregation scenario, each data source is weighted by its reliability. For instance, a data provider may submit abnormal data. Then, the weight of this provider should be lower than the normal ones. In WAAS, the i-th provider’s weight is denoted by a non-integral number . All of the weights of the providers are stored in TA represented as a weight vector . Moreover, the sum of all of the weights is , which is also kept by the TA. In addition, the plaintext of mobile users’ data also could be represented by a vector . We can regard the weight vector as a batch of messages, which has no difference between the users’ data vector . Therefore, the weighted sum of the dataset is the inner product of and . Similar to the basic aggregation scheme, we first calculate weighted sum . Details are shown as follows.
User generates ciphertext: Similar to the basic scheme, the data should be encrypted before sending to the cloud server. Specifically, each user encrypts his or her health data at time point through the following three steps:
- Step 1: computes the hash value at the time point .
- Step 2: encrypts the message through calculating , where is a random number. Furthermore, we set for some (unknown) .
- Step 3: submits the ciphertext to one of the working cloud server.
TA generates ciphertext of : The weight vector directly reflects the importance of each message and the reliability of every user. Therefore, should be encrypted, as well. Specifically, TA encrypts at time point through the following three steps:
- Step 1: TA computes the hash value at the time point .
- Step 2: TA encrypts the i-th weight through calculating , where is a random number. Furthermore, we set for some (unknown) . Thus, the weight vector’s ciphertext is
- Step 3: TA submits the ciphertext to one of the working cloud server.
Privacy-preserving computing of : One of the working cloud servers receives all of the users’ encrypted health data and . According to the privacy requirements, the cloud server needs to compute the encrypted weighted sum without knowing the plaintext of any specific message. By utilizing the homomorphic property of Boneh–Goh–Nissim, we can obtain the encrypted aggregation sum as follows.
As introduced in Section 3.1, anyone can multiply two encrypted messages once using the bilinear map. Let and . Then, we have:
where . We note that the cryptosystem is still additively homomorphic in . Thus, we can compute as:
Since the plaintext of weighted sum , we have:
Joint decryption of : Exactly the same as the basic scheme, TA randomly chooses cloud servers as the working servers. As mentioned above, one cloud server calculates and sends it to the other l working cloud servers. Upon receiving at time point , cloud servers decrypt together. Eventually, we have:
where .
Since , we have . Nevertheless, T is the range of the message, and it is large enough; we let . Thus, the CS can obtain the weighted sum of users’ health data , by computing the discrete logarithm of based on in the expected time . At last, the CS sends to TA.
Result release under differential privacy: Similar to the basic scheme, TA is responsible for computing the final result and releasing it under differential privacy. Once TA receives , TA can get the weighted average value by simply calculating . Generally, TA adds noise to M by leveraging the Laplace mechanism. Let be a random variable, and . Here, is the Laplace noise, which will be added to M, and is the largest weight of users. Then, TA simply computes . Finally, is returned to the data analyst (HIs) as the final result. We can assert that the released result is ϵ-differentially private. The formal proof of differential privacy is given in Section 5.
4.1.4. Privacy-Enhanced Average Aggregation Scheme
In the basic and weighted average aggregation schemes, one of the cloud servers is able to learn the sum of users’ data. Consequently, the cloud server may leak the sensitive statistical information to the unauthorized users. On addressing the problem, we design a privacy-enhanced average aggregation protocol.
First of all, let us recall the basic aggregation scheme (BAAS). Once all of the encrypted data are gathered by several cloud servers, one of the randomly chosen servers can access the decrypted summation of the dataset. In this scheme, all of the cloud servers are curious about the content of the data. Hence, the plaintext of the summation is under the risk of being disclosed. PAAS is designed to address the above problem.
In the initial phase, TA generates additional private keys for each user. Then, each user encrypts the message using private keys. The user generates two ciphertexts for one message and sends them to the cloud. The cloud then calculates two summations for one dataset. Since both summations are permutated by the additional private keys, the cloud cannot access the real summation of the dataset. TA recovers the original summation by solving an equation set. Actually, TA only needs to compute a polynomial.
Details of the scheme are shown as follows.
TA generates private keys for users: TA firstly generates additional private keys for mobile users. In order to strictly protect the privacy of the user, TA assigns each user a unique . A user’s could be a function of the serial number i. For instance, the i-th registered user’s can be set as or some other functions. For simplicity, we set . Thus, each user’s just is the serial number i. Then, TA generates the i-th user’s private keys and through computing . Here, are four random integers created by TA. Then, TA sends to the i-th user as its additional private keys.
User generates ciphertext: Each user encrypts his or her health data at time point through the following three steps:
- Step 1: computes the hash value at the time point .
- Step 2: encrypts through calculating , where is a random number. Furthermore, we set for some (unknown) . Moreover, private keys are encrypted in the same way .
- Step 3: Let and . creates the ciphertexts of as follows.where and .
- Step 4: submits the ciphertexts of to one working cloud server .
Privacy-preserving computing of and : receives all of the users’ encrypted health data. Since each user submits two ciphertexts of the message , needs to compute the encrypted sum twice. By utilizing the homomorphic property of Boneh–Goh–Nissim, we can obtain the encrypted aggregation sum and as follows,
Joint decryption of and : As mentioned above, the cloud sever calculates and . Then, sends them to the other l working cloud servers. Upon receiving and at time point , cloud servers decrypt and together. Finally, we have:
Since , we have and . Nevertheless, T is the range of the message, and it is large enough; we let and . Thus, the CS can obtain and by computing the discrete logarithm of and based on in expected time . At last, the CS sends and to TA.
Result release under differential privacy: TA is responsible for computing the final result and releasing it under differential privacy. Once TA receives and , TA can get the data sum by solving the following equation set,
Based on the above equation set, we can deduce that:
Here, are four integers generated by TA. Therefore, the solution of the equation set is . Therefore, the average value of the dataset is .
Similarly, TA adds noise to M by utilizing the Laplace mechanism. Let be a random variable, and . is the Laplace noise, which will be added to M. Then, TA simply calculates . Finally, is returned to the data analyst (HIs) as the final result. Moreover, is ϵ-differentially private. Since the aggregation function of PAAS is exactly the same as BAAS, the differential privacy is guaranteed.
4.2. Non-Additive Aggregation of Health Data
In reality, non-additive aggregation results are widely applied in cloud-assisted WBAN systems; for instance, min/max, median, histogram, etc. In this section, we propose a scheme for these aggregation tasks. The same as the scheme proposed in [6], the comparison of the data is accomplished in the plaintext environment. In fact, if one wants to obtain the non-additive aggregation results of a encrypted dataset without decrypting it, order-preserving encryption techniques may be applied. Because the comparison is the basic operation, which cannot be finished without knowing the order information of the data, therefore the decryption of the specific message in the cloud servers is inevitable.
Different from [6], all of the decrypted messages are gathered by TA. Thus, the distribution of the data is protected by TA, and cloud servers cannot get access to it. First, one user encrypts its message . Second, sends to the cloud server. Here, we use to represent the ciphertext of . Third, working cloud servers are randomly chosen to decrypt the message. At last, the plaintext of each message is uploaded to TA. Thus, TA gathers all of the users’ messages . In [6], the scheme stores all of the plaintext of the messages in one cloud server. If this cloud server is compromised, all of the users’ personal health information may be leaked. For the privacy consideration, we let TA store the plaintext of the whole dataset.
Once TA has gathered all of the users’ messages , it sorts ’s elements. Then, TA uses an array to store the ordered messages. For instance, the minimum message is , and the maximum is . Note that the first element of array is empty. Therefore, we have .
Based on the ordered array , we can easily deduce that the median message is , if k is odd. When k is even, . As mentioned above, the minimum and maximum messages are , . In [6], noises are added to the result of min/max and median aggregations. However, the scale of the noises is too large, because the sensitivities of min/max and median aggregations are . Since healthcare institutions (HIs) provide health services based on these data, the min/max and median values of users’ health data are required to be as accurate as possible. Thus, TA releases and directly to the HIs. In the following paragraphs, we will show how to accomplish histogram aggregation and release it with differential privacy guaranty.
4.2.1. Hierarchical Method for Histogram
In this part, we provide the histogram aggregation protocol. The histogram is widely used to reflect the distribution of dataset in statistics. Specifically, each bin of a histogram illustrates the frequency of the values falling into it. As shown in Figure 2a, the first bin’s value is 50. Each bin’s value is the count of the hypertensive patients of a certain age group. Since TA has the ordered messages , it can easily obtain the values of the bins in the histogram. Then, TA answers the query submitted by the healthcare institutions based on the histogram. Note that the original histogram can directly reflect the distribution of the dataset. In order to protect the sensitive information, we add noises to the result of the query. Besides, we leverage the post-processing technique [12] to boost the accuracy. Details of query sequence generation, the differential privacy mechanism and post-processing are shown in the following paragraphs.
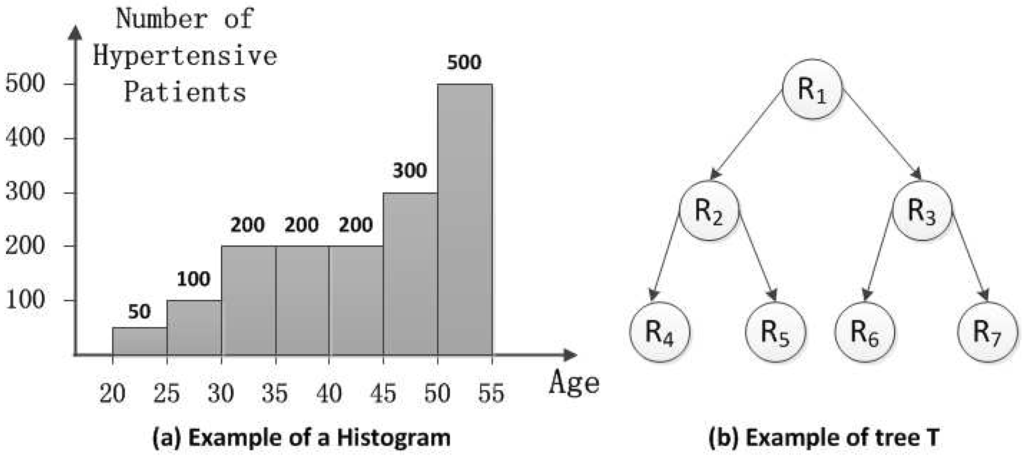
Figure 2.
(a) Example of a histogram. (b) Example of query tree T.
Query sequence generation: A query sequence is proposed by the HIs, which not only asks for unit-length intervals (e.g., single data bin), but also asks for larger intervals (e.g., age from 20–45 in Figure 2a). In this strategy, the larger intervals are a linear combination of the few counts of sub-intervals. The query sequence consists of a batch of hierarchical intervals denoted as a vector .
Moreover, the intervals can be arranged into a tree T, where the unit-length intervals are the leaves. Each node in the tree corresponds to an interval with s children. The node v’s children are equally-sized sub-intervals. We use to denote the case of a query tree with n leaves. If t denotes the height of the tree and s is the branch factor, then . The sequence is ordered by a breadth-first traversal of the tree. Here, we give an example of tree T associated with query sequence for .
As shown in Figure 2b, the query sequence is . Each query is arranged into the tree T whose value is the sum of its children. For instance, the root () is the whole range of the histogram equal to .
Once TA receives the query sequence , it computes each query from the leaf to the root of tree T. We use to represent the result of query on message array .
Add noises to the query sequence: To answer under differential privacy, the first step is to analyze the sensitivity of . When users alter one record, the count changes within through the same level. As the level of the tree is t, the output of changes at most. Thus, . By the aforementioned inference and basic Laplace mechanism, the following algorithm satisfies ϵ-differential privacy:
where m is the length of sequence .
Problem of consistency: The property of consistency will be broken after adding noises to the query results. Because the noises added are randomly produced, there may be a noisy count that does not equal the sum of its sub-intervals. Therefore, cannot be the final output.
Post-processing of query sequence: This step is aimed to derive a consistent and more accurate query result denoted as . We adopt the method proposed by [12]. As summarized in [18], this technique can be dissected into two steps: weighted averaging and mean consistency.
Weighted averaging: First, we need to ensure a fact depicted as the following sentences:
Given two random variables X and Y, consider . When , the variance of Z gets the minimum and minimal variance, which is .
Let be the noisy value of node at level t of tree T. To estimate the node’s noisy value, we use the weighted average of its original noisy value and the sum of its children’s count. Let be the transformed count and be the set of v’s children.
Mean consistency: The mean consistency step aims at ensuring that for each node, its children values sum up to be the same as the parent. Let u be the parent of v.
After post-processing, each node’s value is a weighted sum of the original noisy values of all nodes in the tree. At last, TA returns the final result to HIs. The formal analysis of differential privacy is given in Section 5.
5. Security and Privacy Analysis
In this section, we will discuss the security and privacy issues involved in PMHA-DP. The adversary model, security and privacy requirements are given in Section 3. Clearly, our mission is to preserve users’ private health data from the adversary and to satisfy all of the security requirements. As mentioned in Section 4, each aggregation scheme (includes BAAS, WAAS, PAAS, HMH) is under a differential privacy guarantee. Therefore, we will show the privacy proof of each scheme in this section. Details are shown as follows.
- The users’ privacy is preserved, even if the communication flows are intercepted by . Specifically, may eavesdrop on the communication flows from users to the cloud servers. However, the mobile users in WBANs are dynamic, and the number of users is large; it is impractical for to do so. Even if the data are captured by at time point , ’s message is encrypted as . Thus, cannot decrypt the ciphertext and obtain the message without private key p. Therefore, we can assert that cannot reveal the private data, even if the communication flows are intercepted.
- cannot reveal the uncompromised users’ private health data. Since the amount of mobile users is quite large in the cloud-assisted WBANs system, would be unlikely to breach users’ privacy through compromising some of the users. We assume that may try to disclose the uncompromised users’ private health data by utilizing the private information and private keys of the compromised users. Namely, is able to obtain some of the users’ private keys and their personal data. However, the privacy of uncompromised users is well guaranteed, and the reasons are listed as follows. First, each mobile user’s private key is generated independently; one can deduce nothing about another user from one user’s private key. Second, the sum of all users’ private keys is transparent to . Even if learns users’ private keys, it still cannot reveal the last user’s private key and health data.
- cannot obtain users’ private health data and the aggregated data, even if l CSs are compromised. In the system initialization phase, TA distributes the private keys to each CS and . In this system, the users’ privacy can be protected when no more than CSs are paralyzed or compromised. According to the “all or nothing” property of secret sharing [17], at least CSs are needed to acquire private key p. Therefore, even if possesses l private keys, it still cannot recover p. Similarly, only has l decryption shares of CSs at most, which are insufficient to recover the aggregated data either. Therefore, cannot expose the aggregated data.
- In the privacy-enhanced scheme, cannot acquire the aggregated data, even if all of the CSs are compromised. First, TA utilizes each user’s to generate ’s additional private key and distributes them through a secure channel. Then, encrypts its message twice by using p and . Then, the working CSs calculate two encrypted sums of all of the data. Moreover, working CSs cannot recover the real sum without knowing each user’s additional private key and four randomly generated numbers . Even if all of these secure parameters and two encrypted sums are leaked to , it still does not know how to build an equation group and compute the real sum. Consequently, the aggregated data are well protected even if all of the CSs are compromised by .
- cannot deduce any individual user’s health data by launching differential attacks on TA. TA is the only entity that can release statistical information to HIs. TA adds Laplace noises to the original aggregated data before release. Therefore, the differential privacy mechanism is only applied on TA. Due to the property of the Laplace mechanism, TA is able to resist differential attacks in each proposed aggregation scheme. The proof of differential privacy is given below.
Here, we give a formal differential privacy proof of each aggregation scheme. First, the proof of BAAS is shown as follows:
Proof (Proof of Differential Privacy).
BAAS directly utilizes the Laplace mechanism [13], which is introduced in Definition 3. Thus, the critical step of privacy proof is calculating the sensitivity of the aggregation function. Here, the output of the function is the average of a dataset. Therefore, we rewrite the function as . Here, is the i-th user’s record of the dataset D, and k is the total number of the users’ data. Let be the neighboring dataset differing from D in at most one record. Therefore, if we want to calculate , we need to analyze the problem from three conditions.
Condition 1.
has one more record m than D. Consider two extreme situations, and , where denotes the largest value of the user’s record. If , . If , . Therefore, we have:
Condition 2.
has one less record m than D. If , . If , . Thus, we have:
Condition 3.
D and have the same number of records, but and are the only different records between them. If and , . If, and , . Then, we have .
Based on the above analysis, we can deduce that:
Since , . Thus, the sensitivity of function f is . According to Definition 3, the algorithm is ϵ-differentially private. ☐
The above analysis indicates that quantifying the sensitivity of the aggregation function is critical. The sensitivity analysis of the weighted average aggregation function (i.e., WAAS) is almost the same as BAAS. Thus, we omit it. Moreover, since the aggregation function of PAAS is exactly the same as BAAS, the differential privacy is guaranteed.
The formal analysis of the differential privacy of HMH is shown as follows:
Proof of Differential Privacy.
The sensitivity of query sequence is well analyzed in Section 4.2. We formalize it as . According to the Laplace mechanism [13], when the added random variable satisfies , the algorithm is ϵ-differential privacy. Note that the post-processing does not consume the privacy budget. ☐
6. Performance Evaluation
In this section, we evaluate the performance of PMHA-DP in terms of functionality, computation and communication overhead. Besides, the error analysis is also provided. We will compare our additive and non-additive aggregation schemes with [6] and [6].
Here, we will give a detailed discussion on the dataset. As we know, once the differential privacy mechanism is chosen, the noise scale is also calibrated. In this paper, we utilize the Laplace mechanism as the building block of the scheme. Hence, the sensitivity of the aggregation function is the only parameter that can directly affect the noise scale (i.e., the accuracy of the result). In reality, there are many different health data, such as the blood pressure, body temperature, heart rate, and so on. Different data types lead to different data ranges and typical sizes. For instance, usually, body temperature is within the range of 35–45 degrees Celsius. For a common person, the mean value of the body temperature is 36.9 Celsius. However, for another kind of health data, such as blood pressure, the data range must be totally different from the body temperature. The maximum of blood pressure should be less than 180 mmHg. In this paper, the maximum of the message should be less than T. Hence, our scheme can be applied for different data types as long as the max value is less than T. In this paper, we only consider the size of the largest message to evaluate the sensitivity and the error of the result. Therefore, the error of each protocol is irrelevant to the type of data. Specifically, we vary the size of the message w () from {12, 13, 14, 15, 16, 17, 18, 19, 20, 21} (w is the length of a message). Once the maximum value and the message amount are both established, we can calculate the mathematical expectation of the square difference of the Laplace mechanism.
6.1. Functionality
In our additive aggregation scheme, we propose a basic scheme that is similar to . Both our scheme and provide an average aggregation protocol. In reality, the weighted average is also widely used. However, to the best knowledge of the authors, their are few reported works in the open literature providing a privacy-preserving weighted average aggregation scheme. We design a weighted average aggregation protocol and provide the final result under differential privacy. Moreover, as the working cloud servers in are able to learn the real value of the aggregated data, some sensitive information may be leaked. On addressing the above problem, we design a privacy-enhanced average aggregation scheme, which protects the real sum of the dataset from all of the cloud servers. Besides, the released result also satisfies differential privacy. The comparison of the functionality between PMHA-DP and is shown in Table 1.

Table 1.
Comparison of the functionality of additive aggregation.
The same as , our non-additive aggregation scheme provides max/min, median and histogram aggregation protocols. As analyzed in Section 4.2, the scale of noise is too large for max/min and median aggregations. Thus, we release the final results without adding noises. Histogram aggregation is well discussed in our paper. We first apply the hierarchical method to answer the query submitted by HIs. Then, for privacy consideration, we add Laplace noises to the result. Furthermore, we leverage the post-processing technique to boost the accuracy of noisy answers. Thus, our histogram aggregation scheme is more practical. The comparison of the functionality between PMHA-DP and is shown in Table 2.

Table 2.
Comparison of the functionality of non-additive aggregation.
6.2. Computational Overhead
For additive aggregation schemes, the computation overhead is clear. Because, the process of the encryption and decryption of the whole aggregation system can be divided into some basic calculations, in this paper, we mainly consider four different kinds of calculations. As shown in Table 3, we use some symbols to denote the time of each operation.

Table 3.
Notations.
In our system, there are three entities that share the total computational overhead: MUs (mobile users), TA and CSs. Consequently, we analyze the computational overhead of and three different additive aggregation protocols of PMHA-DP in the above three aspects. Details are shown as follows.
In this paper, the TA has to bear some computational tasks. We have tried our best to reduce the computational burden of TA. As we know, the encrypted data are outsourced to the public cloud. Most aggregation operations are finished by the cloud. However, the cloud servers are honest-but-curious, which may learn the content of the data. Therefore, some sensitive information of the dataset should not be disclosed to the cloud servers. TA is assigned to add noises to the original query result, such as the summation of the data. Due to the property of the Laplace mechanism, the noise scale is proportional to the sensitivity of the aggregation function. Once the privacy budget is set, it is easy to obtain the sensitivity. The sensitivity of an aggregation function can directly reflect the distribution of a dataset. For instance, if the sensitivity of a function is about 37, we can deduce that the dataset is the body temperature. Furthermore, the TA only needs to add noises to the final result, and it is irrelevant regarding the number of users. The time complexity of adding noises is O(1).
For WAAS, TA needs to store the weights of the users and encrypt them before sending them to the cloud servers. Each user’s weight is personal information, and it should be protected from the public cloud. When the system is running for the first time, TA needs to encrypt all of the users’s weights. After the first time, TA only needs to do some partial modifications, which can significantly reduce the computational burden.
For PAAS, the additional calculation of TA is computing the summation of the data. TA can obtain the sum by calculating a simple polynomial. The time complexity is O(1).
Computation overhead of BAAS: Each MU encrypts the health data with one modular multiplication and two modular exponential operations. Therefore, each MU’s total computational overhead is . One of the working CSs gathers all of the MUs’ messages by taking modular multiplication, that is . Then, all of the working CSs calculate the decryption shares with modular exponential operations. Next, one randomly chosen CS gathers the decryption, shares and decrypts it using Pollard’s lambda method, which takes . Therefore, the total computational overhead of working CSs is . TA’s computation burden is light and negligible in the basic scheme.
Computation overhead of WAAS: Each MU encrypts the private data with time . TA encrypts each MU’s weight with time , and there are k users. Therefore, the total time of TA is . Then, all of the working CSs calculate the encrypted weighted sum of the dataset with k bilinear map operations and modular multiplication, that is . At last, CSs jointly decrypt the aggregated data with the same time of the basic scheme: . Therefore, the total computation overhead of CSs is .
Computation overhead of PAAS: Each user encrypts the message with time . Then, the user preprocesses the additional private keys with time . Finally, the user generates the ciphertext of with two bilinear map operations. Thus, the total time of each user is . In the privacy-enhanced scheme, working CSs need to calculate the sum of all users’ messages twice and jointly decrypt them. Therefore, the total computational overhead of CSs is two times that of the basic scheme, that is . TA’s computation burden is negligible and is irrelevant to the scale of the dataset.
Computation overhead of : In [6], each individual MU encrypts the health data with two modular exponential operations and one modular multiplication. Therefore, the total overhead of an MU is . The aggregator SP’soverhead is . The working CSs jointly decrypt the aggregated data with time .
The comparison of the computational overhead is shown in Table 4.

Table 4.
Comparison of the computational overhead. BAAS, basic average aggregation scheme; WAAS, weighted average aggregation scheme; PAAS, privacy-enhanced aggregation scheme; MU, mobile user; CS, cloud server; TA, trusted authority.
We utilize OpenSSL Library [19] to conduct our experiment on a 2.65-GHz processor, 4 GB memory, computing machine. We let the security parameter and set message’s bit length as . Besides, we let the user number range from 10,000–100,000. One CS can provide service for 2500 users at most. The result of the experiment showed that the bilinear map operation and Pollard’s lambda method are quit time consuming. Specifically, we have the results ms, ms and ms. Besides, is directly proportional to . When , ms. Based on these results, we depict the variation of computational overheads in terms of k in Figure 3 and Figure 4.
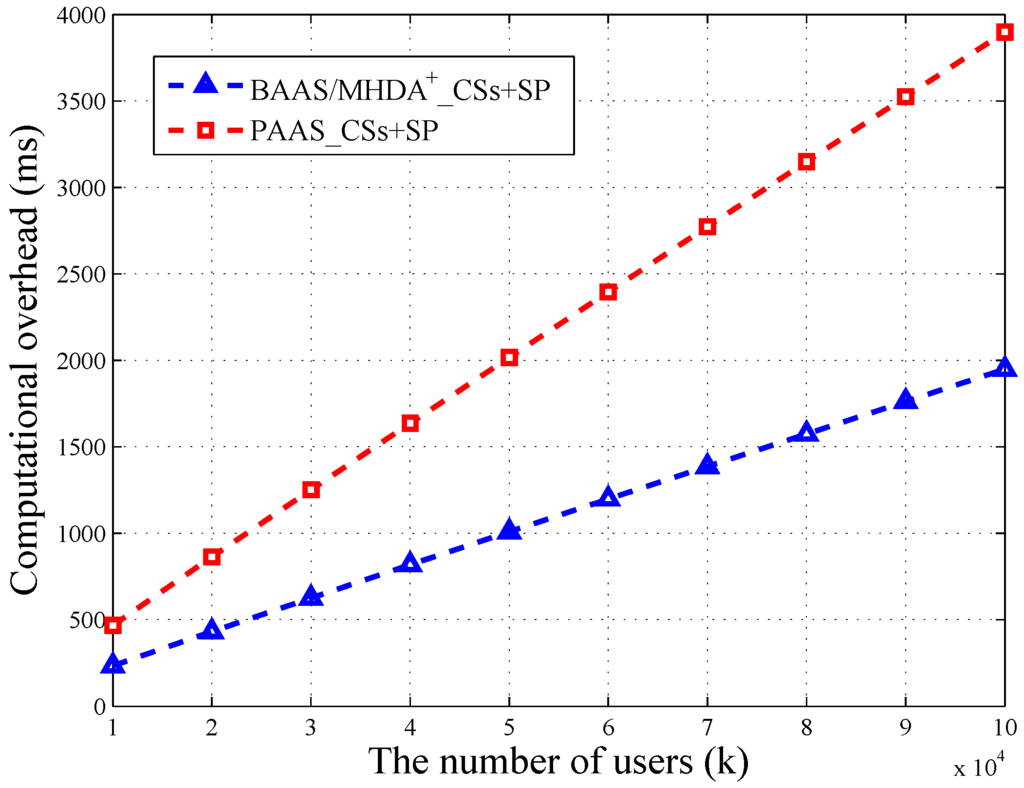
Figure 3.
The computational overhead of BAAS, PAAS and [6].
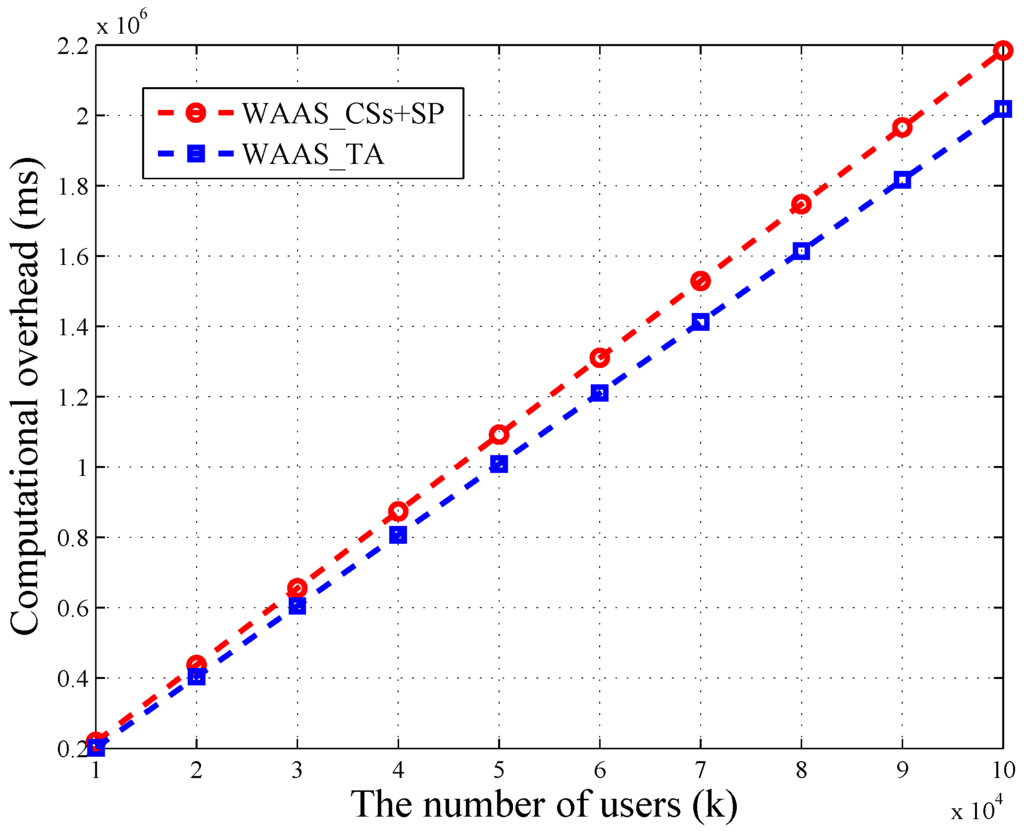
Figure 4.
The computational overhead of TA and CSs + SP in WAAS.
As shown in Figure 3, the computational overhead of CSs + SP in the basic scheme (BAAS) is exactly the same as . Therefore, we use the same line to depict the variation. We can find that the overhead of the privacy-enhanced scheme (PAAS) is two times that of BAAS and . When the user number is 100,000, PAAS’s computational overhead is 3898.80 ms, nearly 4 s. Besides, ’s overhead is 1949.40 ms, nearly 2 s. Therefore, the privacy-enhanced scheme takes up an extra 2 s of calculating time, which is acceptable. Even in the big data environment, suppose the user number reaches 10 million; the calculating time of PAAS is 363,159.64 ms, nearly six minutes. Consider that the high-performance servers in the cloud and part of the computation burden can be uniformly distributed; it is possible to reduce the running time into the acceptable range. Thus, PAAS protects the aggregated data at a low price.
As depicted in Figure 4, the time consumption of TA and CSs + SP in WAAS increases linearly with the number of users. Besides, the loads of TA and CSs are balanced. When the amount of users reaches 100,000, the computational overhead of TA is 2018 s, which is close to CSs’ 2184 s. In WAAS, CSs need to do k bilinear map operations, and TA is required to take modular exponential operations. These two calculations are time consuming, but both of them can be completed in parallel. Thus, it is possible to reduce the running time.
6.3. Communication Overhead
First, we compare the communication overhead of the proposed additive aggregation schemes with . As we know, the length of the ciphertext directly reflects the communication overhead. Therefore, the communication cost of each entity (TA MUs CSs) in BAAS is the same as . In WAAS, the additional communication burden is carried by TA. TA needs to send all of the encrypted weights of MUs to CSs. Actually, in a system, one user’s weight cannot be set by himself or herself. Thus, some control centers like TA are bound to manage all of the users’ weight, and the communication cost is inevitable. In PAAS, each user needs to generate two ciphertexts for one message. Thus, the communication cost of MU is two times that of .
For the proposed non-additive aggregation schemes (NAS) and , the communication overhead can be considered in the communication of each MU. In NAS, MU reports its own encrypt message to CSs. However, MU in submits the ciphertext to SP instead. The length of MU’s ciphertext in is a linear function of the size of the plaintext w. That is , where τ is the security parameter. However, the size of MU’s ciphertext in NAS is a constant .
Actually, each MU’s packet also contains some other information, such as time stamp, user ID, and so on. However, the message occupies the most space of one packet. Therefore, we only consider the message’s communication overhead. As shown in Figure 5, we vary w from and illustrate the communication cost of PAAS, NAS, and in terms of w. The size of MU’s encrypted data in NAS is the same as . Thus, we use the same line to depict them. Similarly, the communication overhead of MU in PAAS is also a constant and is irrelevant to w. However, each MU in PAAS needs to generate two ciphertext for one message. Therefore, PAAS has twice the communication overhead of NAS and , that is . For , the overhead of MU increases linearly with the growing of w. Namely, the longer the message, the larger the communication overhead. Thus, NAS and PAAS are more practical when the message’s size is large.
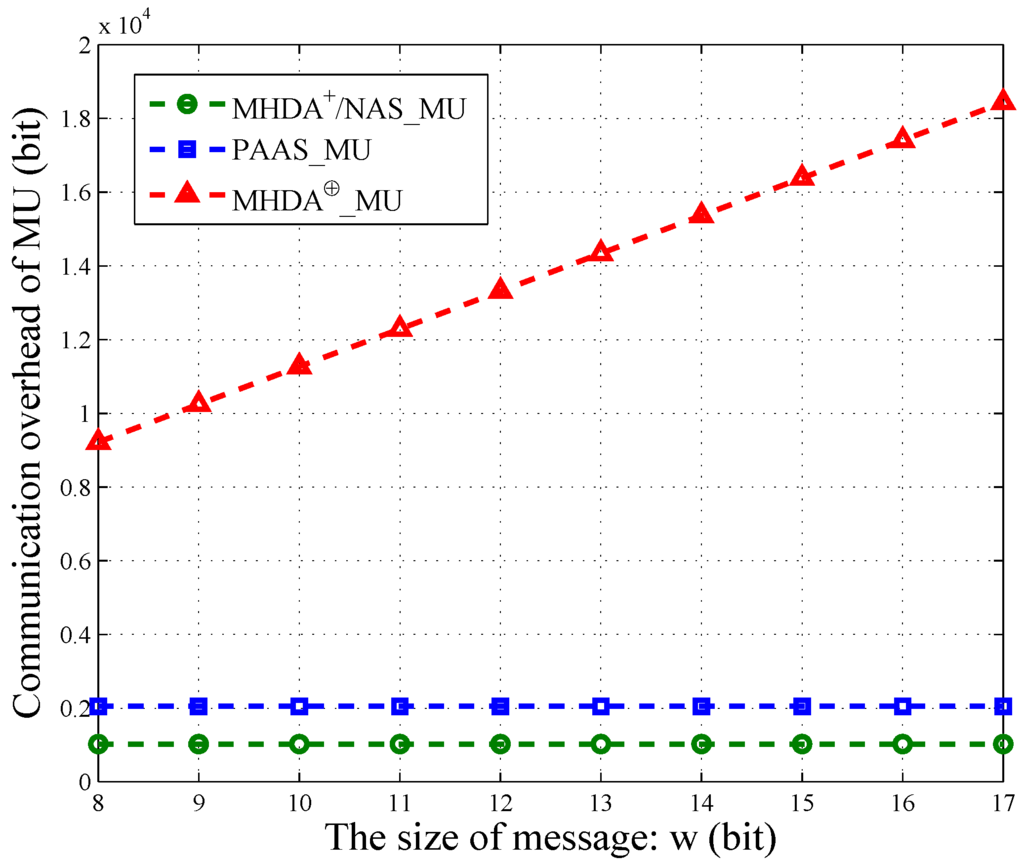
Figure 5.
The communication overhead of MU in [6], [6], PAAS and NAS.
6.4. Error Analysis
In our additive schemes, we directly add noise to the result M. Then, we obtain the noisy answer , where . In this section, we use to represent any aggregation function’s sensitivity. Thus, the mathematical expectation of the square difference of the Laplace mechanism is , which simplifies to: . Since , we have . As discussed in Section 4.1, the aggregation functions of BAAS and PAAS are the same, and the sensitivity of both functions is . In WAAS, . Thus, the errors of BAAS and PAAS are . We also have .
In our non-additive scheme, we choose not to add noise to the result of max/min and median aggregations; because the sensitivity of the function will be too large and is irrelevant to k, that is . However, in , the authors choose to add noises with a large scale. Therefore, we can deduce that the error of max/min and median aggregation in is . In the reality, the number of the users (k) is much larger than 10,000 or even more. Therefore, the error of max/min and median in should be larger than , which is unacceptable. For our histogram aggregation scheme HMH, the sensitivity is , where t is the level of the query tree T. Thus, we have , where m is the length of the query vector .
In , the authors directly add noise to the sum of the health data. Therefore, the sensitivity is T. However, in , the noisy sum is divided by k to acquire the noisy average. Therefore, we can deduce that the sensitivity of the mean value function in is . Note that the noises in are sampled from the geometric distribution . Its probability density function is:
where and . Let X be the noise sampled from . Then, the error of is , which is calculated as follows.
Let , and . We can deduce . Then, we have . Since and , the final result can be calculated as:
The errors of PMHA-DP and [6] are clearly listed in Table 5.

Table 5.
Comparison of the error.
In Table 5, is the largest weight of all of the mobile users. Therefore, must be larger than the average of all of the users’ weights. Then, , which can be transformed into . Therefore, the error of WAAS is greater than or equal to that of PAAS and BAAS. The noise of is sampled from the symmetric geometric distribution, which is a discrete approximation of the Laplace distribution. Consequently, the errors of , BAAS and PAAS can be considered equivalent approximate. Let . We vary k from {10,000, 20,000, 30,000, 40,000, 50,000, 60,000, 70,000, 80,000, 90,000, 100,000} and vary w () from {12,13,14,15,16,17,18,19,20,21} to calculate the error of and BAAS/PAAS. All of the error values of and BAAS/PAAS are listed in Table 6. Apparently, the difference between and is negligible.

Table 6.
List of error values.
Here, we give a detailed discussion on the dataset. As mentioned above, the sensitivity of the average aggregation function and the number of the messages are the only parameters that can directly affect the noise scale. In reality, there are many different health data, such as blood pressure, body temperature, heart rate, and so on. Different data types lead to different data ranges and typical sizes. For instance, usually, the body temperature is within the range 35 °C–45 °C. For a common person, the mean value of the body temperature is 36.9 °C. However, for another kind of health data, such as blood pressure, the data range must be totally different from the body temperature. The maximum of blood pressure should be less than 180 mmHg. In this paper, the maximum of the message should be less than T. We only consider the size of the largest message to evaluate the sensitivity and the error of the result. Therefore, the error listed in Table 6 is irrelevant to the type of data. Specifically, once the maximum value and the message amount are both established, we can calculate the mathematical expectation of the square difference of the Laplace mechanism.
In HMH, we improve the accuracy of the query through consistency. According to [12], for all query sequences, and there exists a query sequence with . As depicted in Figure 6 and Figure 7, the error of changes significantly along with the level and branch of query tree T, when and . Thus, post-processing makes more accurate on some query sequences.
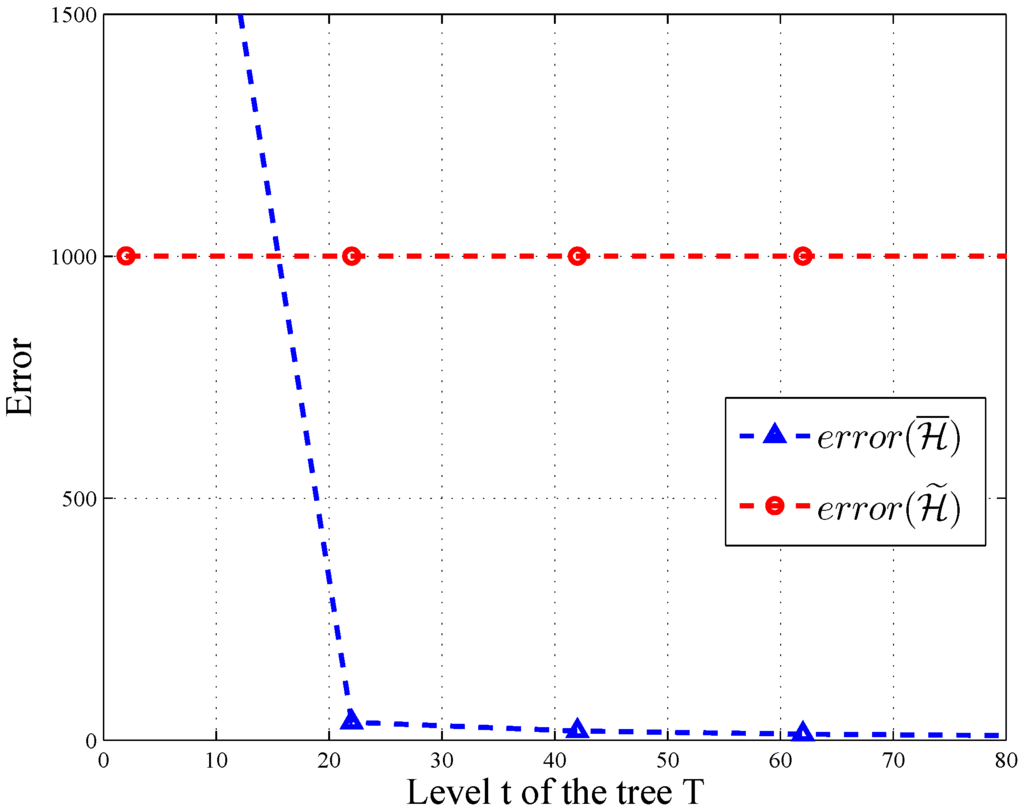
Figure 6.
Error varies with the level.
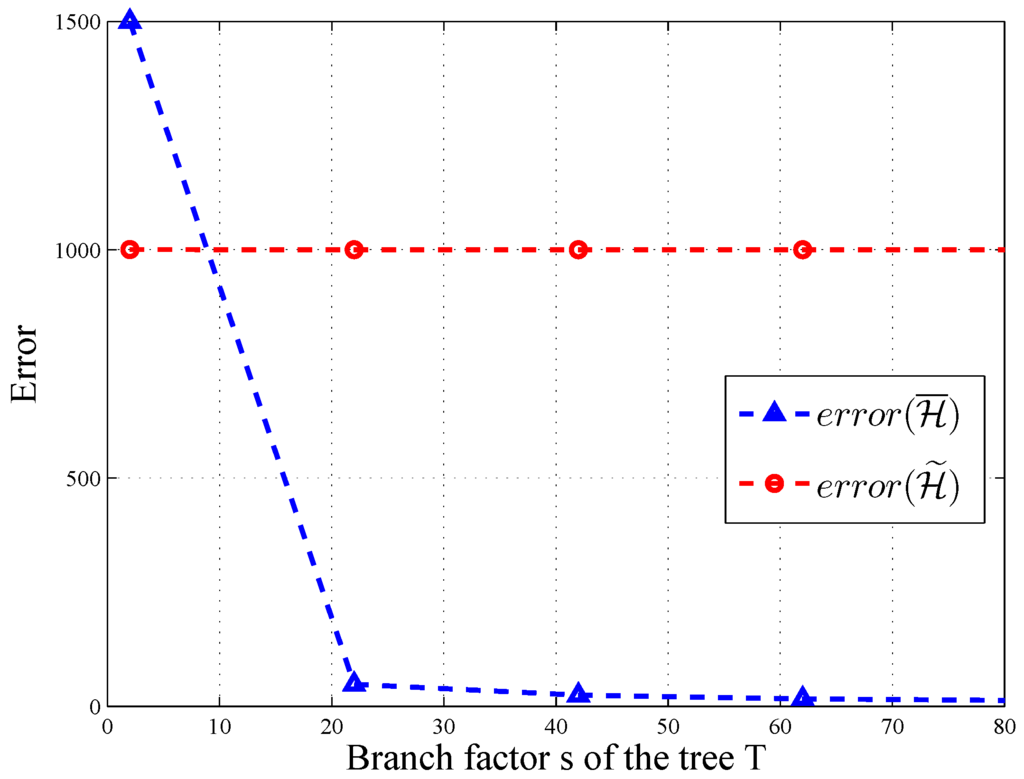
Figure 7.
Error varies with the branch.
Another typical way to evaluate the error is to issue queries on the data before and after using differential privacy and measuring the difference between these query results. Therefore, we also give a further analysis of the error by leveraging a popular metric called the relative error [6]. This metric can directly reflect the difference between the original result and the permutated result. The mathematical expectation of the relative error η is calculated as follows.

Table 7.
Comparison of the relative error.
As analyzed above, the error of WAAS is greater than or equal to that of PAAS and BAAS. Moreover, the errors of , BAAS and PAAS can be considered equivalent approximately. Here, we assume that the data type is the body temperature. Let , T = 45 °C (i.e., the maximum temperature of human) and the average temperature M = 37 °C. Suppose the number of users is . Then, the relative error of BAAS/PAAS is , which is almost the same as , that is . Therefore, the difference between BAAS/PAAS and is negligible.
7. Further Discussion
In this section, we will discuss four special issues related to our work.
The first issue is temporal aggregation, which is the aggregation of the same user’s data at different time points. In this paper, we recognize the average aggregation as a representative function of additive aggregation. Specifically, we only give the spatial aggregation schemes, which is the aggregation of the different users at the same time point. Actually, the temporal aggregation is similar to spatial aggregation. The servers can just multiply all of the corresponding user’s encrypted health data to obtain the encrypted sum. Moreover, the jointly decryption of the encrypted sum is exactly the same as the spatial aggregation.
The second issue is fault tolerance. The computational missions are assigned to CSs in PMHA-DP, and the total number of CSs is more than . According to the adversary model, no more than l servers could be compromised. Therefore, at least servers can accomplish computational tasks. Hence, our scheme supports fault tolerance of CS failures. BAAS supports the user failures. When some users refuse to report their health data, the CSs only need to record the number of normal users and calculate the encrypted sum as usual. Then, TA divides the sum by the number of normal users to acquire the average value. Our non-additive schemes also support fault tolerance of user failures. In WAAS, CSs can report the abnormal users’ weights to TA. Then, TA is able to figure out the total weight of the normal users. Thus, the weighted average of normal users can be calculated by TA. Therefore, both WAAS and PAAS support fault tolerance of user failures; because TA can still obtain the normal users’ sum through solving Equation (19). In a word, PMHA-DP achieves some functions and supports fault tolerance simultaneously.
The third issue is data type. PMHA-DP can be extended to some other scenarios with different data types; such as salary, age, height and some other short personal record. As we know, the Boneh–Goh–Nissim cryptosystem applied in this scheme is a homomorphic public key encryption scheme. The same as the other public key cryptosystem, it also suffers from low efficiency of encryption and decryption. Thus, it is often used to encrypt some short messages. Moreover, the proposed solution cannot be adapted to the scenario of file encryption and some other kinds of huge messages. If a user wants to encrypt one’s own video file before outsourcing it to the cloud, the secret key cryptosystem may be a better choice.
The fourth issue is data tampering. The compromised users may send tampered data to the cloud servers. For instance, a malicious user may send some abnormal data to the cloud (e.g., a compromised user may set his or her temperature as 100 °C), which directly impacts the aggregation result. These abnormal data are not easy to detect under the ciphertext environment, and it will indeed decrease the accuracy of the statistics. How to kick out the compromised users and detect the tampered data are both challengeable problems. Several data aggregation schemes [6] are suffering from these problems, as well. At present, we have no practical solution. Therefore, these problems are important, and we will push a further study them in future work.
8. Related Work
Cloud-assited WBANs is evolved from the traditional wireless sensor networks (WSNs) [20,21,22], which is widely used in healthcare applications. Actually, some cryptology-based techniques, such as key evolution [23], public verification [24], searchable encryption [25] and user authentication [26], can also be applied in the cloud-assisted WBANs. We will make in-depth study on these techniques in the future. However, in this section, we mainly introduce the state-of-the-art works closely related to our paper. We first review the privacy-preserving data aggregation schemes and then recall some about differential privacy.
Privacy-preserving data aggregation is a kind of cryptology-based technique, which aims at protecting sensitive data. In [8], Lu et al. provide an efficient aggregation scheme called EPPA. It structures multi-dimensional data into a ciphertext by utilizing a super-increasing sequence. Due to the batch verification technique, EPPA significantly decreases the communication and computational overheads. However, the fault tolerance and differential privacy are not supported. In [9], Chen et al. present PDAFT , which supports both spatial and temporal aggregation. Moreover, PDAFT also supports fault tolerance. However, it does not provide multifunctional aggregation and differential privacy guarantees. In [27], Li et al. leverage a novel key management technique to support large plaintext space. Their scheme can accomplish min aggregation, which can be extended to max aggregation. However, it fails to support multifunctional aggregation and fault tolerance. Chen et al. [10] propose a scheme called MuDA . It supports variance aggregation and one-way ANOVA aggregation with differential privacy. Besides, MuDA leads to less communication overhead than the scheme proposed by Shi et al. [28]. However, MuDA cannot support fault tolerance either.
Han et al. [6] present a multifunctional aggregation scheme with fault tolerance called PPM-HDA. PPM-HDA supports both temporal and spatial aggregation. Besides, the differential privacy mechanism is also applied. However, there are still some functions, like weighted average and histogram aggregation, which are not discussed in [6].
Differential privacy [29,30,31] is a promising technique that can achieve a mathematically-precise guarantee of privacy. In [13], Dwork et al. classify data release under differential privacy into two different models: interactive and non-interactive [32,33]. Dwork et al. [13] proposed the widely-used Laplace mechanism.
The private histogram reflects the data distribution. The results can be used for statistical query or other linear queries. Many works are done by using the private histogram. For instance, Blum et al. [32] construct a one-dimensional histogram by dividing the input counts into several bins, where the counts in each bin are approximately equal. Meanwhile, Xiao et al. explore a wavelet-based approach to handle multi-dimensional dataset. In [34], Xu et al. develop several methods of building an optimal histogram under ϵ-differential privacy. Multi-dimensional partitioning strategies for differential private histogram release can be found in [35]. Recently, Li et al. [36] proposed a new histogram publish scheme that achieve higher accuracy. However, these schemes are lacking efficiency in the histogram partition and data update.
Some differential privacy mechanisms take post-processing to reduce the noise scale. Boosting the accuracy of the query through consistency is feasible. Barak et al. [37] firstly make a contribution to it. Moreover, Hey et al. [12] answered histogram queries by a basic hierarchical method. They also apply the technique of constrained inference to improve query accuracy. Recently, Lee et al. [38] formulated the post-processing step as a constrained maximum likelihood estimation problem, which is equivalent to constrained minimization. The proposed scheme is suitable for a wide variety of applications, including differential private contingency tables, histograms and linear queries.
9. Conclusions
In this paper, we propose a privacy-enhanced and multifunctional health data aggregation scheme, which is able to support fault tolerance. Specifically, we utilize the cloud-assisted WBANs system as our storage, computation and communication supporter. The proposed scheme achieves additive and non-additive aggregation simultaneously. We provide a few new aggregation functions and protect the aggregated data from the CSs. The performance evaluation indicates that the communication and computational overhead is reduced. For the future work, we are going to focus on the data aggregation techniques in the environment of big data. We will try to achieve some other functions and boost the efficiency of the scheme.
Acknowledgments
This work is supported by the National Natural Science Foundation of China under Grants 61472065 and U1333127, the International Science and Technology Cooperation and Exchange Program of Sichuan Province, China, under Grant 2014HH0029, the China Postdoctoral Science Foundation funded project under Grants 2014M552336 and 2015T80972, the Fundamental Research Funds for Chinese Central Universities under Grant ZYGX2015J056, the State Key Laboratory of Information Security foundation Open Foundation under Grant 2015-MS-02 and the Open Research Project of the State Key Laboratory of Industrial Control Technology, Zhejiang University, China (No. ICT1600220)
Author Contributions
Hao Ren and Hongwei Li contributed to the conception of the study. Hao Ren performed the data analyses and wrote the manuscript; Xiaohui Liang and Shibo He contributed significantly to analysis and manuscript preparation; Lian Zhao helped perform the analysis with constructive discussions. Yuanshun Dai provided some important suggestions about the paper organization.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, P.; Ding, Z.; Jiang, C.; Zhou, M. Design and Implementation of a Web-Service-Based Public-Oriented Personalized Health Care Platform. IEEE Trans. Syst. Man Cybern. Syst. 2013, 43, 941–957. [Google Scholar] [CrossRef]
- Cavallari, R.; Martelli, F.; Rosini, R.; Buratti, C.; Verdone, R. A Survey on Wireless Body Area Networks: Technologies and Design Challenges. IEEE Commun. Surv. Tutor. 2014, 16, 1635–1657. [Google Scholar] [CrossRef]
- Movassaghi, S.; Abolhasan, M.; Lipman, J.; Smith, D.; Jamalipour, A. Wireless Body Area Networks: A Survey. IEEE Commun. Surv. Tutor. 2014, 16, 1658–1686. [Google Scholar] [CrossRef]
- Liu, B.; Yan, Z.; Chen, C.W. MAC protocol in wireless body area networks for E-health: Challenges and a context-aware design. IEEE Wirel. Commun. 2013, 20, 64–72. [Google Scholar]
- Kline, N.; Snodgrass, R.T. Computing temporal aggregates. In Proceedings of the International Conference on Data Engineering, Taipei, Taiwan, 6–10 March 1995; pp. 222–231.
- Han, S.; Zhao, S.; Li, Q.; Ju, C.; Zhou, W. PPM-HDA: Privacy-preserving and multifunctional health data aggregation with fault tolerance for cloud assisted WBANs. IEEE Trans. Inf. Forensics Secur. 2015, 11, 1940–1955. [Google Scholar] [CrossRef]
- Jia, W.; Zhu, H.; Cao, Z.; Dong, X.; Xiao, C. Human-Factor-Aware Privacy-Preserving Aggregation in Smart Grid. IEEE Syst. J. 2014, 8, 598–607. [Google Scholar] [CrossRef]
- Lu, R.; Liang, X.; Li, X.; Lin, X.; Shen, X. EPPA: An Efficient and Privacy-Preserving Aggregation Scheme for Secure Smart Grid Communications. IEEE Trans. Parallel Distrib. Syst. 2012, 23, 1621–1631. [Google Scholar]
- Chen, L.; Lu, R.; Cao, Z. PDAFT: A privacy-preserving data aggregation scheme with fault tolerance for smart grid communications. Peer-to-Peer Netw. Appl. 2014, 8, 1122–1132. [Google Scholar] [CrossRef]
- Chen, L.; Lu, R.; Cao, Z.; AlHarbi, K.; Lin, X. MuDA: Multifunctional data aggregation in privacy-preserving smart grid communications. Peer-to-Peer Netw. Appl. 2014, 8, 777–792. [Google Scholar] [CrossRef]
- Dwork, C. Differential Privacy. In Automata, Languages and Programming; Springer: Berlin, Germany; Heidelberg, Germany, 2006; Volume 4052, pp. 1–12. [Google Scholar]
- Hay, M.; Rastogi, V.; Miklau, G.; Suciu, D. Boosting the accuracy of differentially private histograms through consistency. Proc. VLDB Endow. 2010, 3, 1021–1032. [Google Scholar] [CrossRef]
- Dwork, C.; McSherry, F.; Nissim, K.; Smith, A. Calibrating noise to sensitivity in private data analysis. In Theory of Cryptography; Springer: Berlin, Germany; Heidelberg, Germany, 2006; pp. 265–284. [Google Scholar]
- Boneh, D.; Goh, E.J.; Nissim, K. Evaluating 2-DNF formulas on ciphertexts. In Theory of Cryptography; Springer: Berlin, Germany; Heidelberg, Germany, 2005; pp. 325–341. [Google Scholar]
- Goyal, V.; Pandey, O.; Sahai, A.; Waters, B. Attribute-based encryption for fine-grained access control of encrypted data. In Proceedings of the ACM Conference on Computer and Communications Security, Alexandria, VA, USA, 30 October–3 November 2006; pp. 89–98.
- Menezes, A.J.; Van Oorschot, P.C.; Vanstone, S.A. Handbook of Applied Cryptography (Discrete Mathematics and Its Applications); CRC Press: Boca Raton, FL, USA, 1997; Volume 6. [Google Scholar]
- Shamir, A. How to Share a Secret. ACM Commun. 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Qardaji, W.; Yang, W.; Li, N. Understanding hierarchical methods for differentially private histograms. Proc. VLDB Endow. 2013, 6, 1954–1965. [Google Scholar] [CrossRef]
- OpenSSL 1.0.2d. Available online: http://www.openssl.org/source/ (accessed on 1 March 2016).
- Liu, A.; Liu, X.; Liu, Y. A comprehensive analysis for fair probability marking based traceback approach in WSNs. In Security and Communication Networks; Wiley Online Library: Hoboken, NJ, USA, 2016; pp. 2448–2475. [Google Scholar]
- Hu, Y.; Liu, A. Improvement the quality of mobile target detection through portion of node with fully duty cycle in WSNs. In Computer Systems Science and Engineering; CRL Publishing: Leicester, UK, 2016; pp. 5–17. [Google Scholar]
- Liu, A.; Hu, Y.; Chen, Z. An Energy-Efficient Mobile Target Detection Scheme with Adjustable Duty Cycles in Wireless Sensor Networks. In International Journal of Ad Hoc and Ubiquitous Computing; Inderscience Publishers: Geneva, Switzerland, 2016; pp. 2448–2475. [Google Scholar]
- Li, H.; Lin, X.; Yang, H.; Liang, X.; Lu, R.; Shen, X. EPPDR: An Efficient Privacy-Preserving Demand Response Scheme with Adaptive Key Evolution in Smart Grid. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 2053–2064. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, C.; Yu, S.; Li, H.; Zhang, X. SCLPV: Secure Certificateless Public Verification for Cloud-Based Cyber-Physical-Social Systems Against Malicious Auditors. IEEE Trans. Comput. Social Syst. 2015, 2, 159–170. [Google Scholar] [CrossRef]
- Li, H.; Liu, D.; Dai, Y.; Luan, T. Engineering Searchable Encryption of Mobile Cloud Networks: When QoE Meets QoP. IEEE Wirel. Commun. 2015, 22, 74–80. [Google Scholar] [CrossRef]
- Li, H.; Lu, R.; Zhou, L.; Yang, B.; Shen, X. An Efficient Merkle-Tree-Based Authentication Scheme for Smart Grid. IEEE Syst. J. 2014, 8, 655–663. [Google Scholar] [CrossRef]
- Li, Q.; Cao, G.; Porta, T.L. Efficient and Privacy-Aware Data Aggregation in Mobile Sensing. IEEE Trans. Dependable Secur. Comput. 2014, 11, 115–129. [Google Scholar] [CrossRef]
- Shi, E.; Chan, T.H.H.; Rieffel, E.G.; Chow, R.; Song, D. Privacy-preserving aggregation of time-serier data. In Proceedings of the 18th Annual Network and Distributed System Security Symposium, San Diego, CA, USA, 6–9 February 2011; Volume 2.
- Blum, A.; Dwork, C.; McSherry, F.; Nissim, K. Practical privacy: The SuLQ framework. In Proceedings of the Twenty-Fourth ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems, Baltimore, MD, USA, 13–16 June 2005; pp. 128–138.
- Dinur, I.; Nissim, K. Revealing information while preserving privacy. In Proceedings of the ACM SIGMOD-SIGACT-SIGART Symposium on PODS, San Diego, CA, USA, 9–12 June 2003; pp. 202–210.
- Dwork, C.; Nissim, K. Privacy-preserving datamining on vertically partitioned databases. In Advances in Cryptology–CRYPTO; Springer: Berlin, Germany; Heidelberg, Germany, 2004; pp. 528–544. [Google Scholar]
- Blum, A.; Ligett, K.; Roth, A. A learning theory approach to noninteractive database privacy. J. ACM 2013, 60, 12. [Google Scholar] [CrossRef]
- Mohammed, N.; Alhadidi, D.; Fung, B.C.; Debbabi, M. Secure Two-Party Differentially Private Data Release for Vertically Partitioned Data. IEEE Trans. Dependable Secur. Comput. 2014, 11, 59–71. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, Z.; Xiao, X.; Yang, Y.; Yu, G.; Winslett, M. Differentially private histogram publication. VLDB J. 2013, 22, 797–822. [Google Scholar] [CrossRef]
- Xiao, Y.; Xiong, L.; Yuan, C. Differentially private data release through multidimensional partitioning. In Secure Data Management; Springer: Berlin, Germany; Heidelberg, Germany, 2010; pp. 150–168. [Google Scholar]
- Li, C.; Hay, M.; Miklau, G.; Wang, Y. A Data- and Workload-Aware Algorithm for Range Queries under Differential Privacy. Proc. VLDB Endow. 2014, 7, 341–352. [Google Scholar] [CrossRef]
- Barak, B.; Chaudhuri, K.; Dwork, C.; Kale, S.; McSherry, F.; Talwar, K. Privacy, accuracy, and consistency too: A holistic solution to contingency table release. In Proceedings of the 26th ACM SIGMOD-SIGACT-SIGART Symposium on PODS, Beijing, China, 11–14 June 2007; pp. 273–282.
- Lee, J.; Wang, Y.; Kifer, D. Maximum likelihood postprocessing for differential privacy under consistency constraints. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 635–644.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).