Relative Estimation of Water Content for Flat-Type Inductive-Based Oil Palm Fruit Maturity Sensor
Abstract
:1. Introduction
2. Design Basic Principles
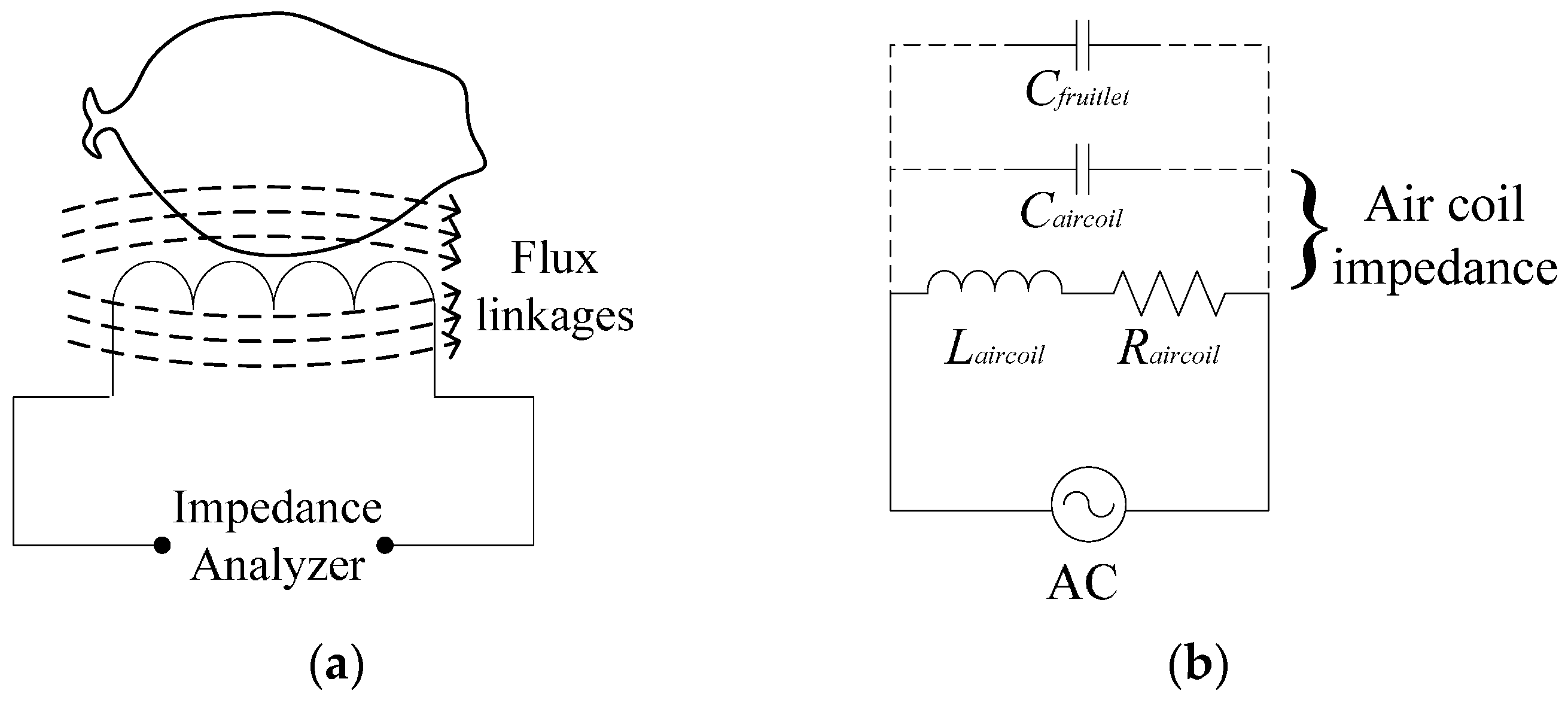
2.1. Electrical Diagram
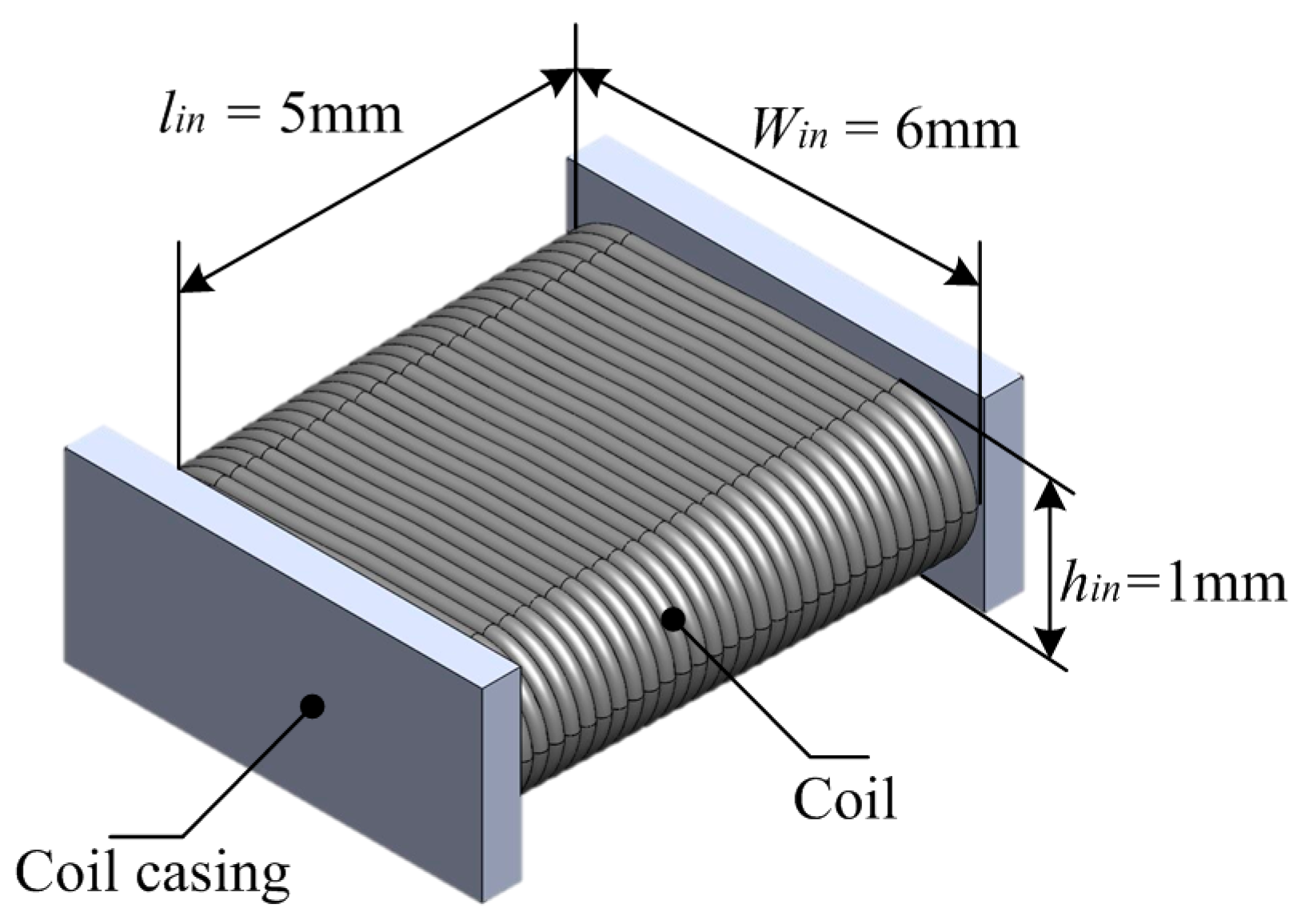
2.2. Sensor’s Structure
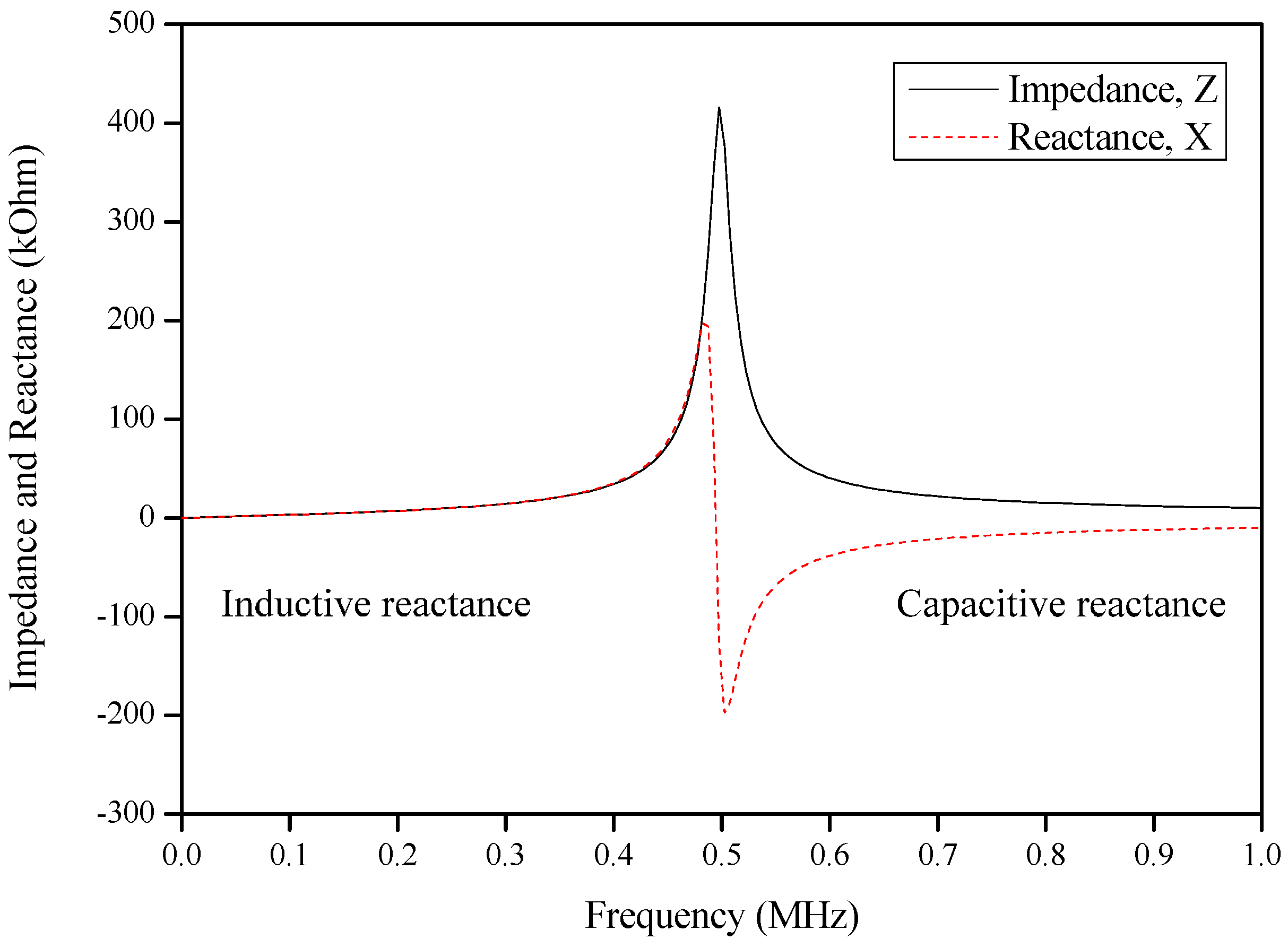
2.3. Resonance Characteristics
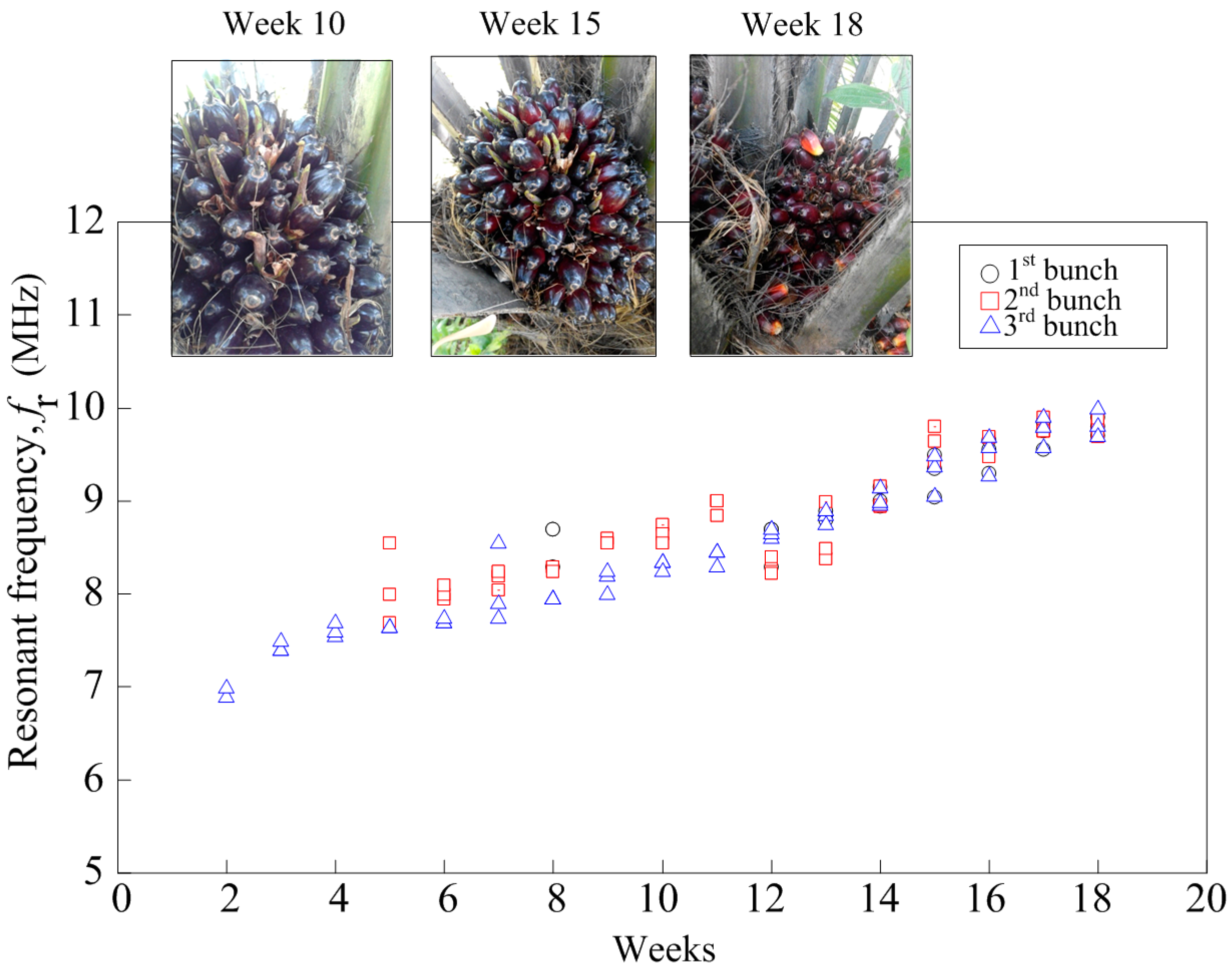
2.4. Fruit Sample
3. Mathematical Analysis
3.1. Inductance Estimation
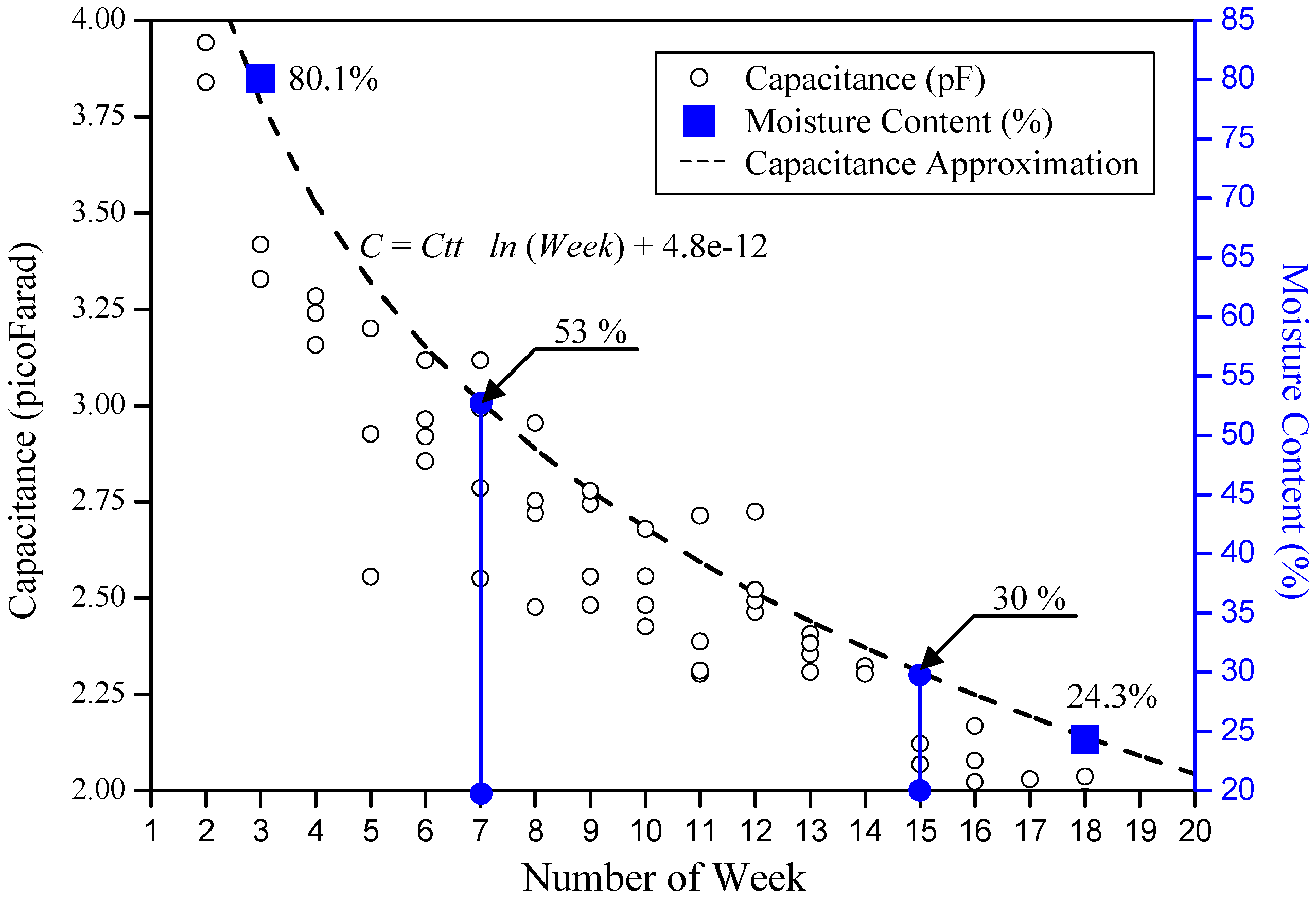
3.2. Self-Capacitance Estimation
4. Results and Discussions
4.1. Calculated Results
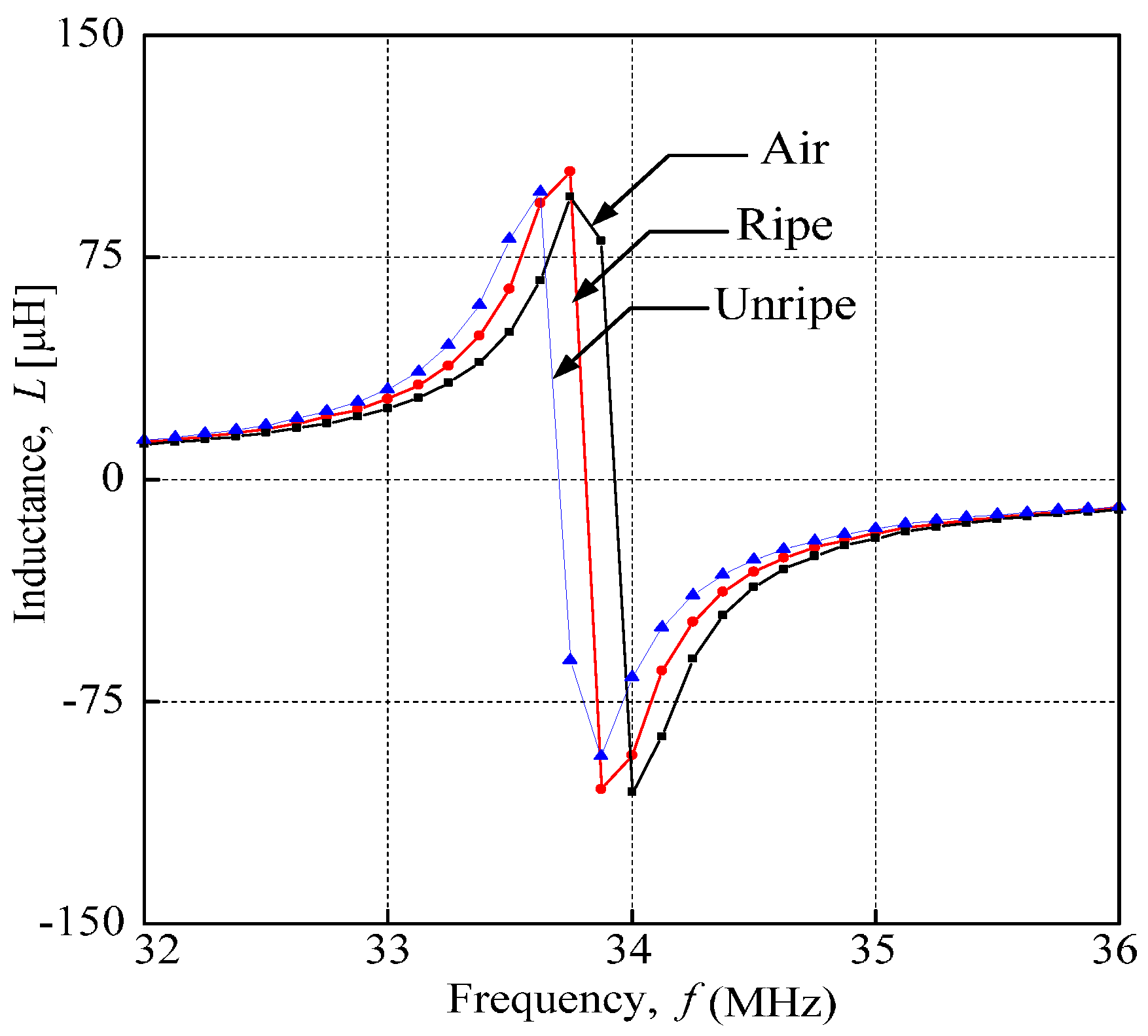
4.2. Field Testing Results and Analysis
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Malaysian Palm Oil Board. Oil Palm Fruit Grading Manual, 2nd ed.; Malaysian Palm Oil Board (MPOB): Bangi, Malaysia, 2003. [Google Scholar]
- Osama, M.B.S.; Sindhuja, S.; Abdul, R.M.S.; Helmi, Z.M.S.; Reza, E.; Meftah, S.A.; Mohd, H.M.H. Classification of oil palm fresh fruit bunches based on their maturity using portable four-band sensor system. Comput. Electron. Agric. 2012, 82, 55–60. [Google Scholar]
- Yeow, Y.K.; Abbas, Z.; Khalid, K. Application of microwave moisture sensor for determination of oil palm fruit ripeness. Meas. Sci. Rev. 2010, 10, 7–14. [Google Scholar] [CrossRef] [Green Version]
- Abbas, Z.; Yeow, Y.K.; Shaari, A.H.; Khalid, K.; Hassan, J.; Saion, E. Complex permittivity and moisture measurements of oil palm fruits using an open-ended coaxial sensor. IEEE Sens. J. 2005, 5, 1281–1287. [Google Scholar] [CrossRef]
- Sharifudin, M.S.; Cardenas-Blanco, A.; Gao Amin, M.H.; Soon, N.G.; Laurance, D.H. Monitoring development and ripeness of oil palm fruit (Elaeis guineensis) by MRI and bulk NMR. Int. J. Agric. Biolog. 2010, 12, 101–105. [Google Scholar]
- Bonnie, T.Y.P.; Mohtar, Y. Determination of palm oil residue in palm kernel and palm oil methyl ester using near infrared spectroscopy. J. Oil Palm Res. 2011, 23, 1055–1059. [Google Scholar]
- Massarini, A.; Kazimierczuk, M.K. Self-capacitance of inductors. IEEE Trans. Power Electron. 1997, 12, 671–676. [Google Scholar] [CrossRef]
- Jakoby, B.; Vellekoop, M.J. Physical sensors for water-in-oil emulsions. Sens. Actuators A. Phys. 2004, 110, 28–32. [Google Scholar] [CrossRef]
- Harun, N.H.; Misron, N.; Sidek, R.M.; Aris, I.; Ahmad, D.; Wakiwaka, H.; Tashiro, K. Investigations on a novel inductive oil palm fruit sensor. Sensors 2014, 14, 2431–2448. [Google Scholar]
- Tashiro, K.; Wakiwaka, H.; Mori, T.; Nakano, R.; Harun, N.H.; Misron, N. Experimental confirmation of cylindrical electromagnetic sensor design for liquid detection application. In Sensing Technology: Current Status and Future Trends IV, 1st ed.; Mason, A., Mukhopadhyay, S., Eds.; Springer International Publishing: Basel, Switzerland, 2015; Volume 12, pp. 119–137. [Google Scholar]


| Parameter/Part | Value/Type |
|---|---|
| Type of Measurement Setup | Series (Ls–Rs) |
| Voltage (mV) | 500 |
| Frequency (MHz) | 0.02–10 |
| Sweep (points) | 200 |
| Coil wire diameter, Do (mm) | 0.12 |
| Number of turns, N | 170 |
| Category | Surface Color | Age (WAA) |
|---|---|---|
| Unripe | Dark purple | After 7 |
| Ripe | Red orange | 18–21 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Misron, N.; Aliteh, N.A.; Harun, N.H.; Tashiro, K.; Sato, T.; Wakiwaka, H. Relative Estimation of Water Content for Flat-Type Inductive-Based Oil Palm Fruit Maturity Sensor. Sensors 2017, 17, 52. https://doi.org/10.3390/s17010052
Misron N, Aliteh NA, Harun NH, Tashiro K, Sato T, Wakiwaka H. Relative Estimation of Water Content for Flat-Type Inductive-Based Oil Palm Fruit Maturity Sensor. Sensors. 2017; 17(1):52. https://doi.org/10.3390/s17010052
Chicago/Turabian StyleMisron, Norhisam, Nor Aziana Aliteh, Noor Hasmiza Harun, Kunihisa Tashiro, Toshiro Sato, and Hiroyuki Wakiwaka. 2017. "Relative Estimation of Water Content for Flat-Type Inductive-Based Oil Palm Fruit Maturity Sensor" Sensors 17, no. 1: 52. https://doi.org/10.3390/s17010052
APA StyleMisron, N., Aliteh, N. A., Harun, N. H., Tashiro, K., Sato, T., & Wakiwaka, H. (2017). Relative Estimation of Water Content for Flat-Type Inductive-Based Oil Palm Fruit Maturity Sensor. Sensors, 17(1), 52. https://doi.org/10.3390/s17010052







