Tracking of Maneuvering Complex Extended Object with Coupled Motion Kinematics and Extension Dynamics Using Range Extent Measurements
Abstract
:1. Introduction
- (a)
- MCEOT using measurements of target’s range extent is first considered explicitly, our approach characterizes not only the evolution of the kinematic state over time, but also the object extension dynamics. More importantly, the coupling between the centroid kinematics and extension evolution (e.g., the close relationship between the turn maneuver of the centroid and the abrupt change of extension) is also explicitly involved.
- (b)
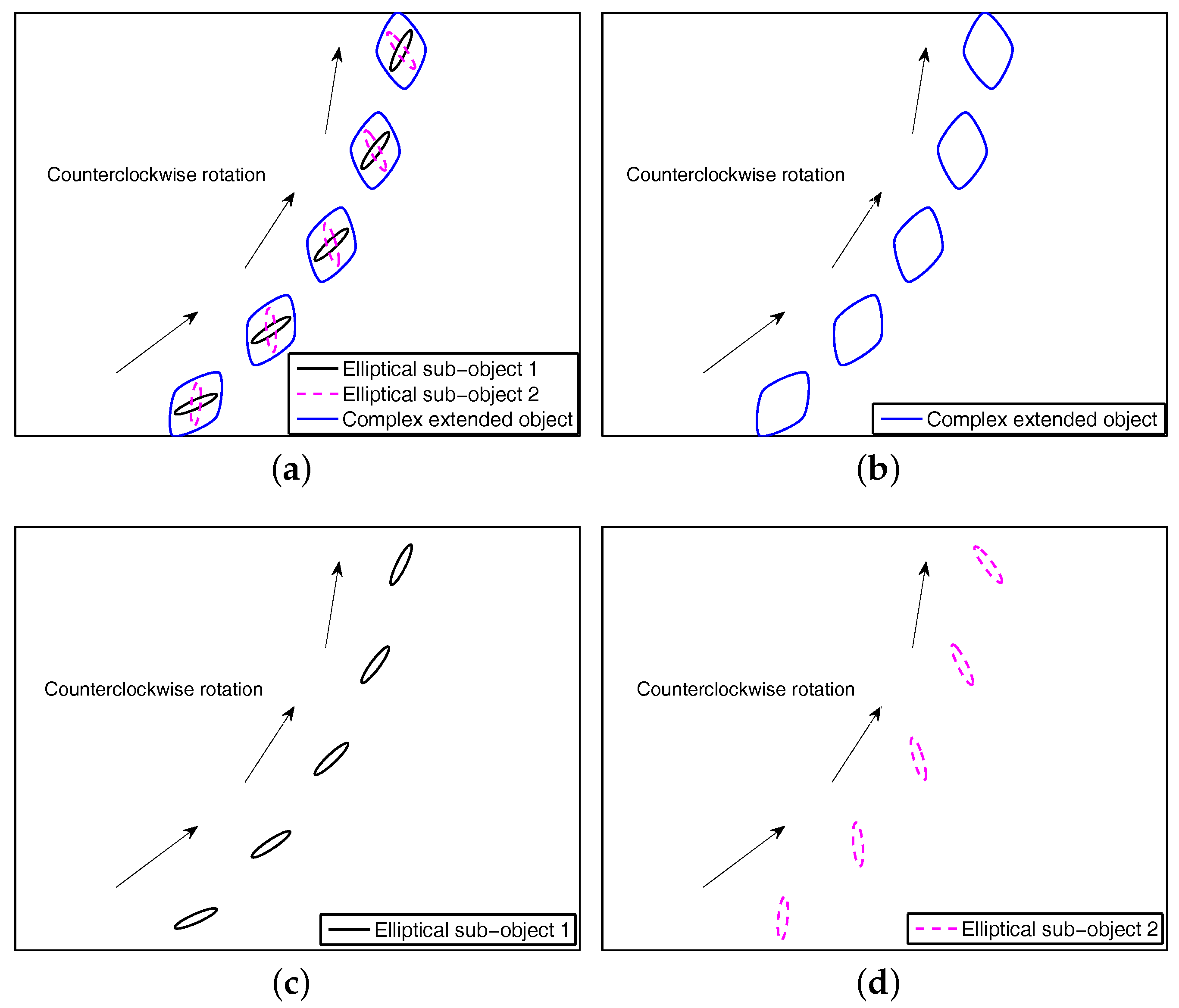
- The new model has a concise and unified form and it can accurately describe an MCEO with a turn maneuver in both the extension dynamics and the centroid kinematics, i.e., the maneuver model of a complex extended object can be obtained and directly represented by that of several simple sub-objects (decomposed using the Minkowski sum) jointly. In particular, the elliptical maneuvering object model is obtained in this paper, which is a by-product of the proposed approach.
- (c)
- Based on the Minkowski sum, different parameterizations can be adopted in our unified modeling framework if they are efficient to describe sub-objects’ extension dynamics. This does not affect the generality of the proposed approaches for solving MCEOT.
- (d)
- Due to the concise linear form, the proposed modeling is easily incorporated into a general tracking architecture, in which the exchange of information between centroid kinematics and extension dynamics are sufficiently utilized. This largely facilitates the derivation and design of an MCEOT algorithm for achieving much better estimation performance.
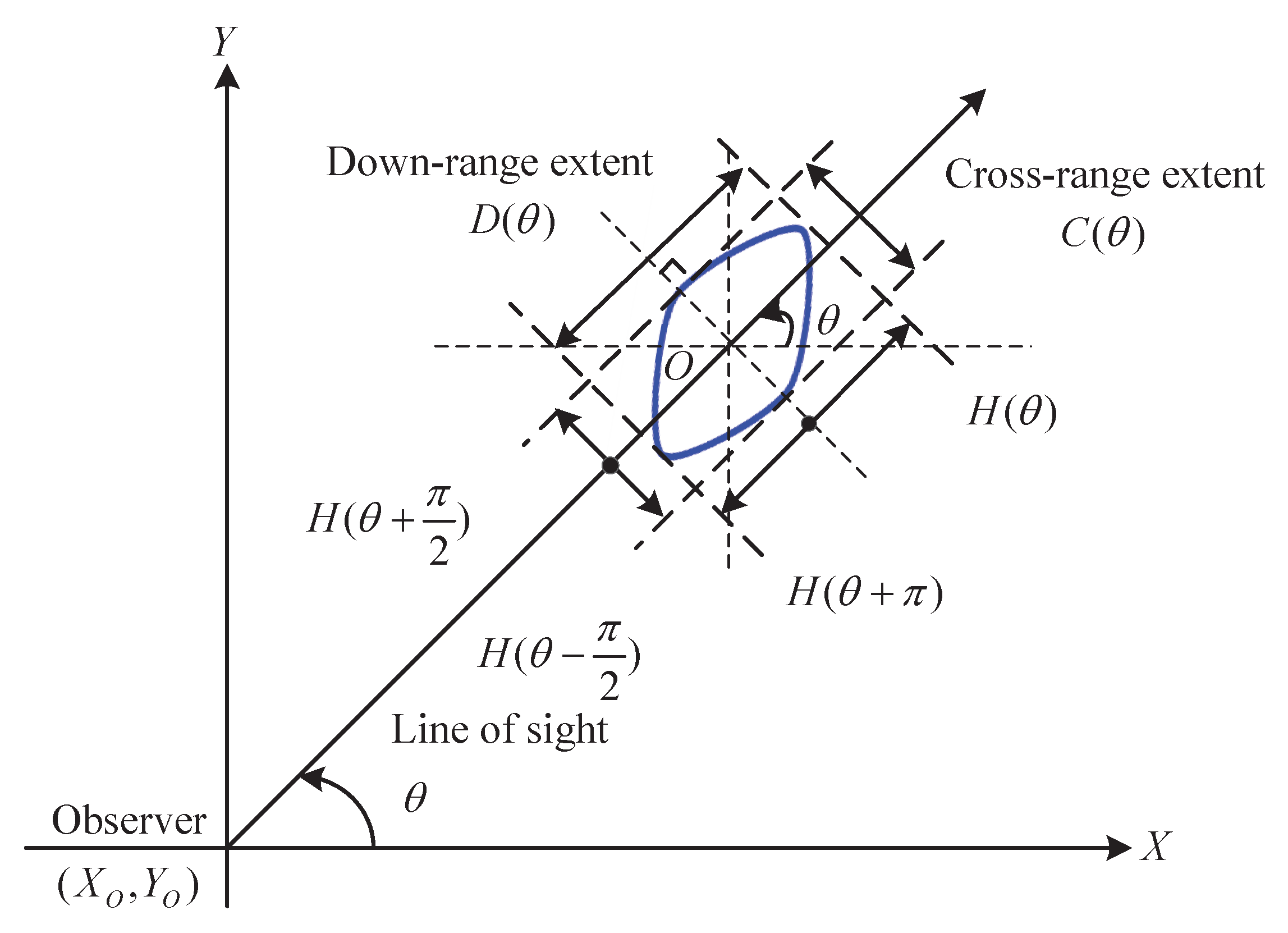
2. Problem Formulation
- (a)
- how to accurately describe the extension dynamics (change in size, shape, orientation, e.g., rotation) of an MCEO over time,
- (b)
- how to deal with the close coupling between the centroid kinematics and extension evolution, and how to embody it in the MCEO modeling.
3. MCEO Modeling Using Range Extent Measurements
3.1. The Unified Complex Extension Dynamics Based on Minkowski Sum
3.2. The Minkowski-Sum-Based Modeling and Estimation for CT Maneuvers with Known Turn Rates
3.3. The Minkowski-Sum-Based Modeling and Estimation for CT Maneuvers with Unknown Turn Rates
3.4. Complexity Analysis
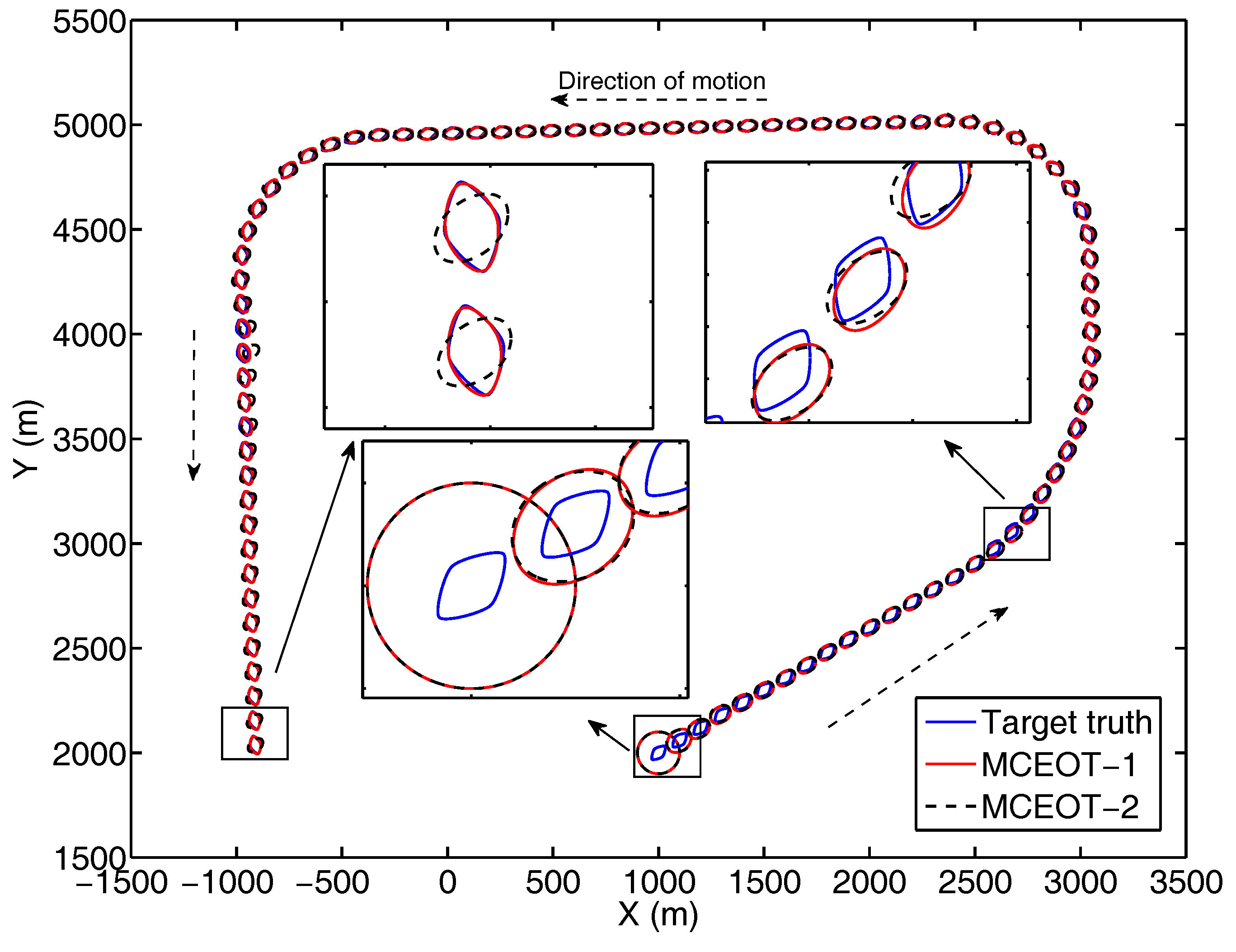
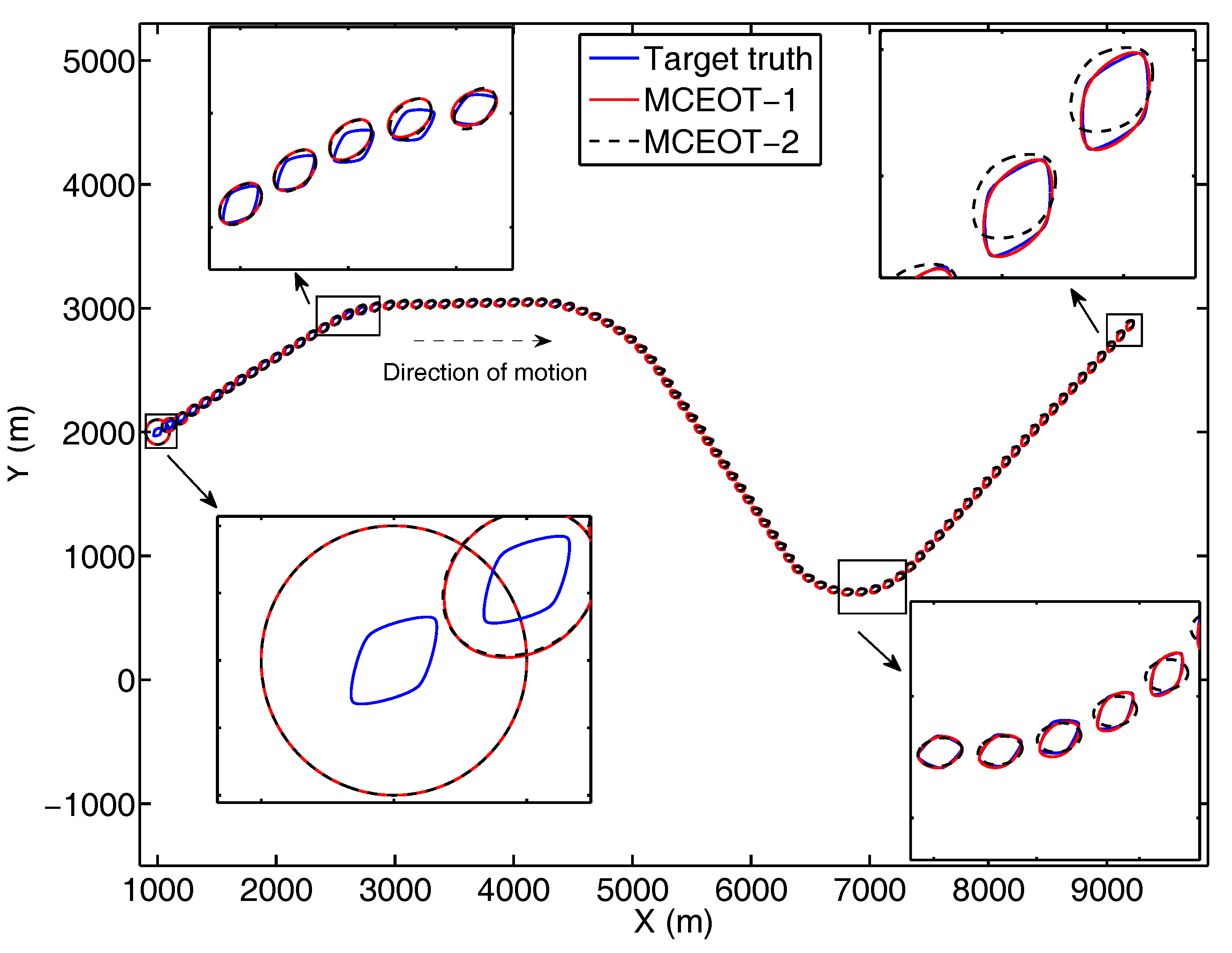
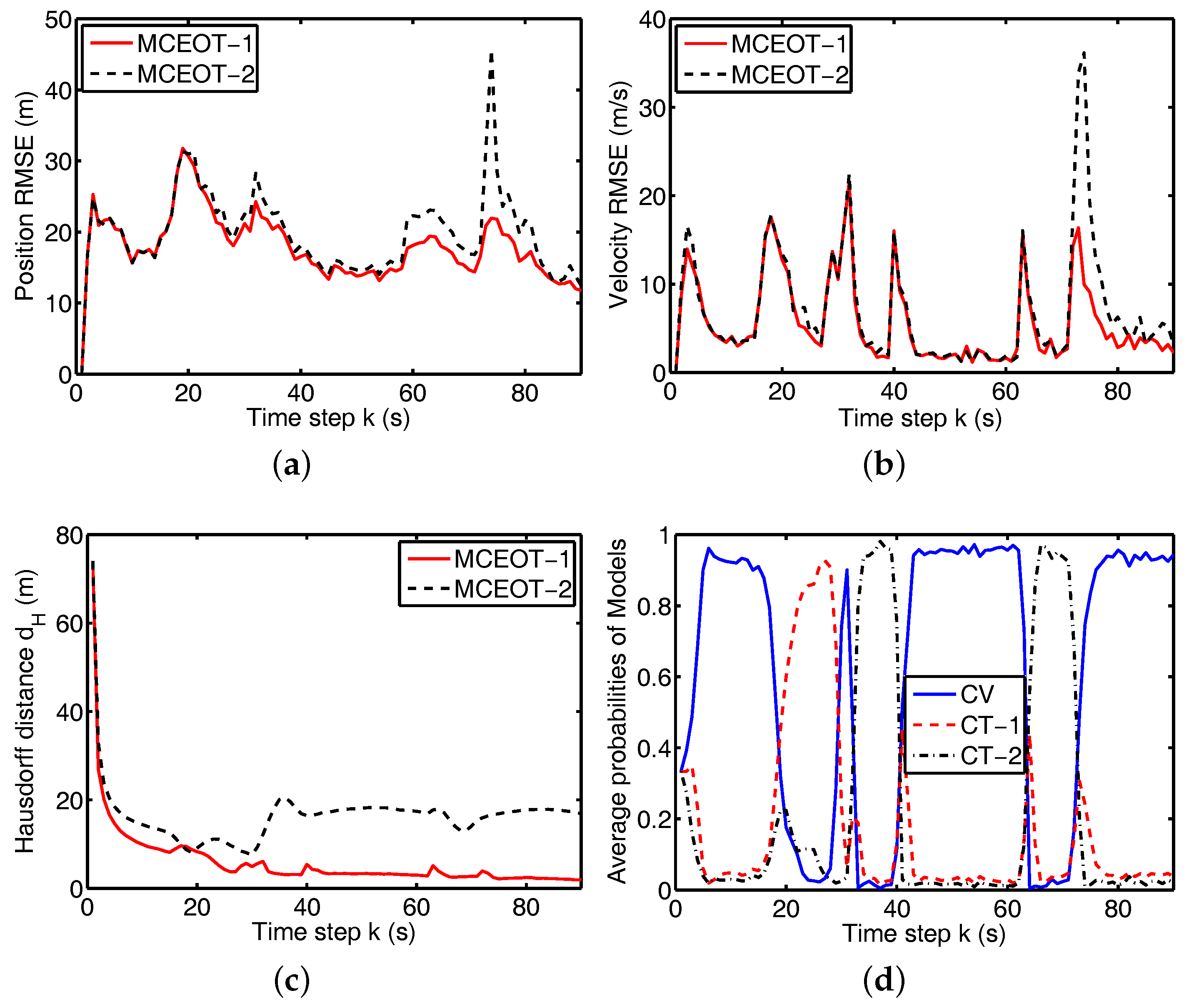
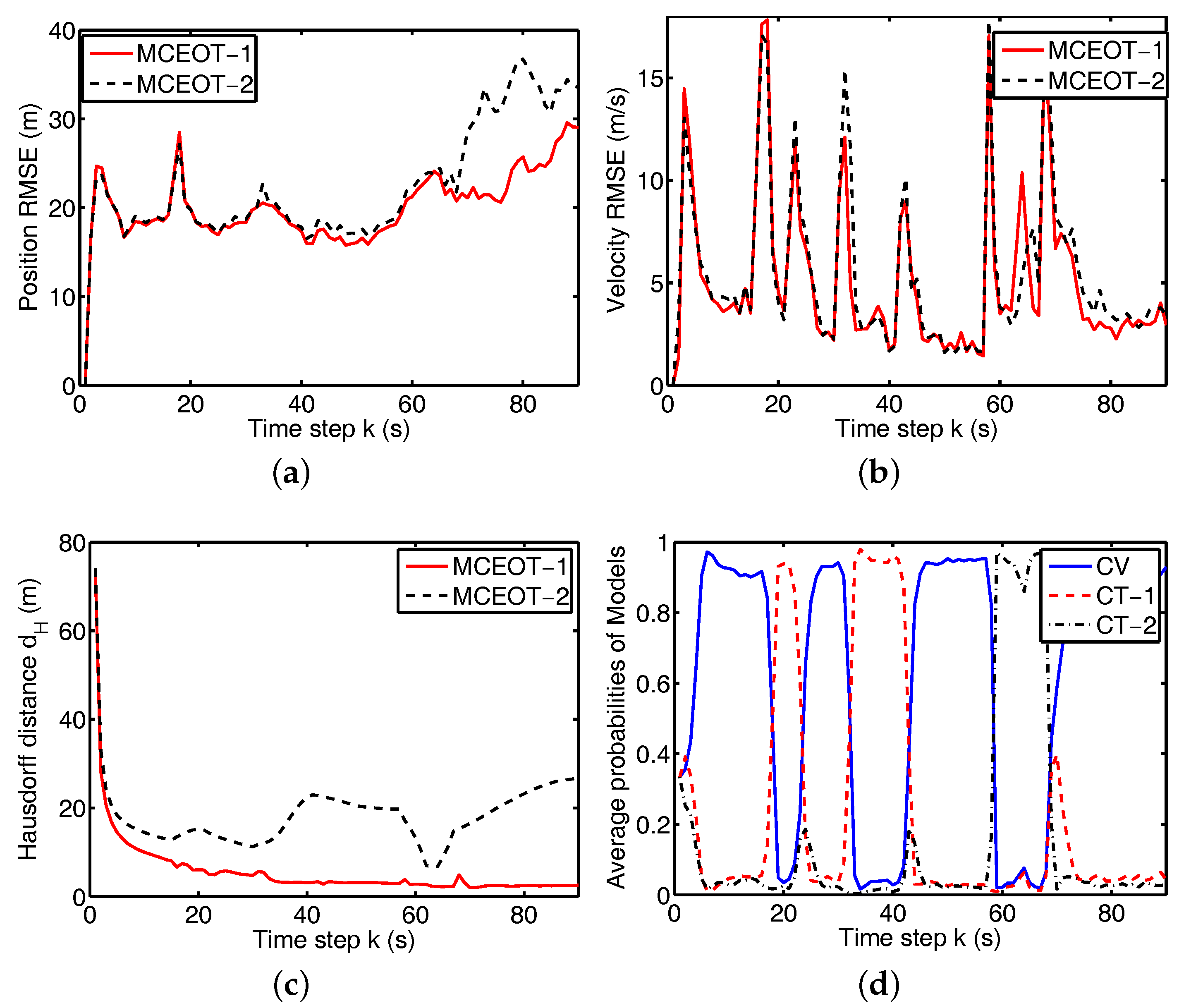
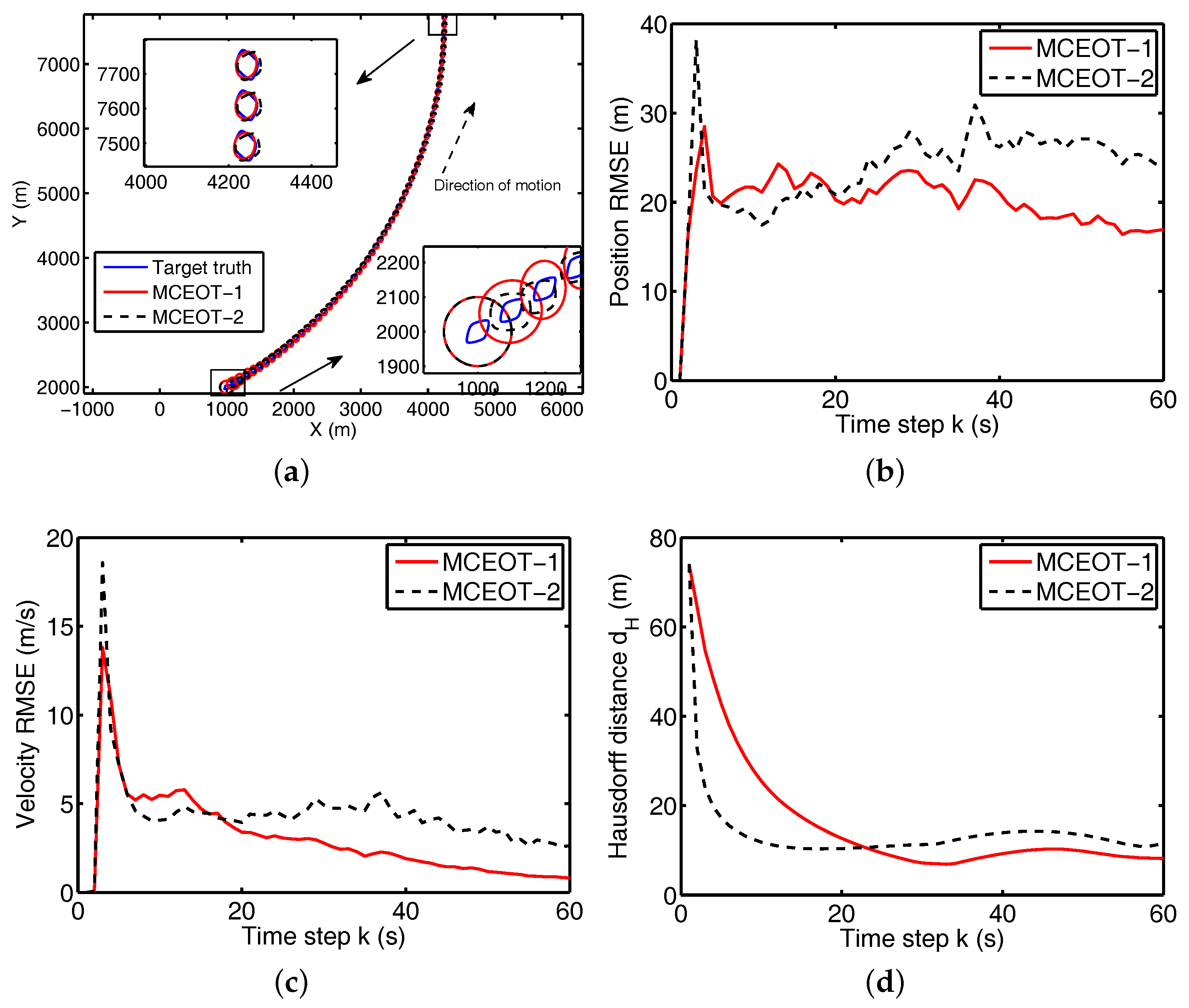
4. Simulation Results and Performance Evaluation
- (a)
- MCEOT-1: The proposed approach based on Minkowski sum considering the highly coupled dynamics of both the state and the extension.
- (b)
- MCEOT-2: The approach considering only the centroid state dynamics.
4.1. Tracking Performance Using Minkowski-Sum-Based CT Model with Known Rates
4.2. Tracking Performance Using Minkowski-Sum-Based CT Model with Unknown Rates
4.3. Performance Comparison and Complexity Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liu, Z.; Wu, D.; Xie, W.; Li, L. Tracking the turn maneuvering target using the multi-target Bayes filter with an adaptive estimation of turn rate. Sensors 2017, 17, 373. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Wu, R. Affinity propagation clustering of measurements for multiple extended target tracking. Sensors 2015, 15, 22646–22659. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Z.; Meng, H.; Zhang, H.; Wang, X. Performance bound for extended target tracking using high resolution sensors. Sensors 2010, 10, 11618–11632. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Mu, C.; Han, S.; Bai, T. Model parameter adaption-based multi-model algorithm for extended object tracking using a random matrix. Sensors 2014, 14, 7505–7523. [Google Scholar] [CrossRef] [PubMed]
- Koch, W.; van Keuk, G. Multiple hypothesis track maintenance with possibly unresolved measurements. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 883–892. [Google Scholar] [CrossRef]
- Gilholm, K.; Salmond, D. Spatial distribution model for tracking extended objects. IEE Proc. Radar Sonar Navig. 2005, 152, 364–371. [Google Scholar] [CrossRef]
- Mahler, R. PHD filters for nonstandard targets, I: Extended targets. In Proceedings of the 12th International Conference on Information Fusion (Fusion 2009), Seattle, WA, USA, 6–9 July 2009. [Google Scholar]
- Lian, F.; Han, C.; Liu, W.; Sun, J. Unified cardinalized probability hypothesis density filters for extended targets and unresolved targets. Signal Process. 2012, 92, 1729–1744. [Google Scholar] [CrossRef]
- Zhang, Y.; Ji, H. A novel fast partitioning algorithm for extended target tracking using a Gaussian mixture PHD filter. Signal Process. 2013, 93, 2975–2985. [Google Scholar] [CrossRef]
- Vo, B.-N.; Mallick, M.; Bar-Shalom, Y.; Coraluppi, S.; Osborne, R.; Mahler, R.; Vo, B.-T. Multitarget tracking. In Wiley Encyclopedia of Electrical and Electronics Engineering; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Koch, W. Bayesian approach to extended object and cluster tracking using random matrices. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 1042–1059. [Google Scholar] [CrossRef]
- Feldmann, M.; Franken, D.; Koch, W. Tracking of extended objects and group targets using random matrices. IEEE Trans. Signal Process. 2011, 59, 1409–1420. [Google Scholar] [CrossRef]
- Lan, J.; Li, X.R. Tracking of maneuvering non-ellipsoidal extended object or target group using random matrix. IEEE Trans. Signal Process. 2014, 62, 2450–2463. [Google Scholar] [CrossRef]
- Lan, J.; Li, X.R. Tracking of extended object or target group using random matrix: New model and approach. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2973–2989. [Google Scholar] [CrossRef]
- Baum, M.; Hanebeck, U.D. Extended object tracking with random hypersurface models. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 149–159. [Google Scholar] [CrossRef]
- Hong, L.; Cui, N.; Pronobis, M.; Scott, S. Local motion feature aided ground moving target tracking with GMTI and HRR measurements. IEEE Trans. Autom. Control 2005, 50, 127–133. [Google Scholar]
- Salmond, D.J.; Parr, M.C. Track maintenance using measurements of target extent. IEE Proc. Radar Sonar Navig. 2003, 150, 389–395. [Google Scholar] [CrossRef]
- Klemm, R. Recognition of convoys with array radar. IET Radar Sonar Navig. 2012, 6, 123–129. [Google Scholar] [CrossRef]
- Angelova, D.; Mihaylova, L. Extended object tracking using Monte Carlo methods. IEEE Trans. Signal Process. 2008, 56, 825–832. [Google Scholar] [CrossRef] [Green Version]
- Ristic, B.; Salmond, D.J. A study of a nonlinear filtering problem for tracking an extended target. In Proceedings of the 7th International Conference on Information Fusion (Fusion 2004), Stockholm, Sweden, 28 June–1 July 2004. [Google Scholar]
- Xu, L.; Li, X.R. Hybrid Cramer-Rao lower bound on tracking ground moving extended target. In Proceedings of the 12th International Conference on Information Fusion (Fusion 2009), Seattle, WA, USA, 6–9 July 2009. [Google Scholar]
- Sun, L.; Li, X.R.; Lan, J. Modeling of extended objects based on support functions and extended Gaussian images for target tracking. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 3021–3035. [Google Scholar] [CrossRef]
- Sun, L.; Lan, J.; Li, X.R. Modeling for tracking of complex extended object using Minkowski addition. In Proceedings of the 17th International Conference on Information Fusion (Fusion 2014), Salamanca, Spain, 7–10 July 2014. [Google Scholar]
- Sun, L.; Lan, J.; Li, X.R. Joint tracking and classification of extended object based on support functions. In Proceedings of the 17th International Conference on Information Fusion (Fusion 2014), Salamanca, Spain, 7–10 July 2014. [Google Scholar]
- Li, X.R.; Jilkov, V.P. Survey of maneuvering target tracking—Part I: Dynamic models. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1333–1364. [Google Scholar]
- Li, X.R.; Jilkov, V.P. Survey of maneuvering target tracking—Part V: Multiple-model methods. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1255–1321. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K. A new method for the nonlinear transformation of means and covariances in filters and estimators. IEEE Trans. Autom. Control. 2000, 45, 477–482. [Google Scholar] [CrossRef]
- Lan, J.; Li, X.R. Nonlinear estimation by LMMSE-based estimation with optimized uncorrelated augmentation. IEEE Trans. Signal Process. 2015, 63, 4270–4283. [Google Scholar] [CrossRef]
- Lan, J.; Li, X.R. Multiple Conversions of Measurements for Nonlinear Estimation. IEEE Trans. Signal Process. 2017, 65, 4956–4970. [Google Scholar] [CrossRef]
- Ito, K.; Xiong, K. Gaussian filters for nonlinear filtering problems. IEEE Trans. Autom. Control 2000, 45, 910–927. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S. Cubature Kalman filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef]
- Baheti, R.; O’Hallaron, D. Efficient parallel implementation of target tracking Kalman filter. In Proceedings of the 27th IEEE Conference on Decision & Control, Austin, TX, USA, 7–9 December 1988; Volume 1, pp. 376–381. [Google Scholar]
- Li, X.R.; Zhao, Z.-L. Evaluation of estimation algorithms. Part I: Incomprehensive performance measures. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 1340–1358. [Google Scholar] [CrossRef]
- Gardner, R.J.; Kiderlen, M.; Milanfar, P. Convergence of algorithms for reconstructing convex bodies and directional measures. Ann. Stat. 2006, 34, 1331–1374. [Google Scholar] [CrossRef]
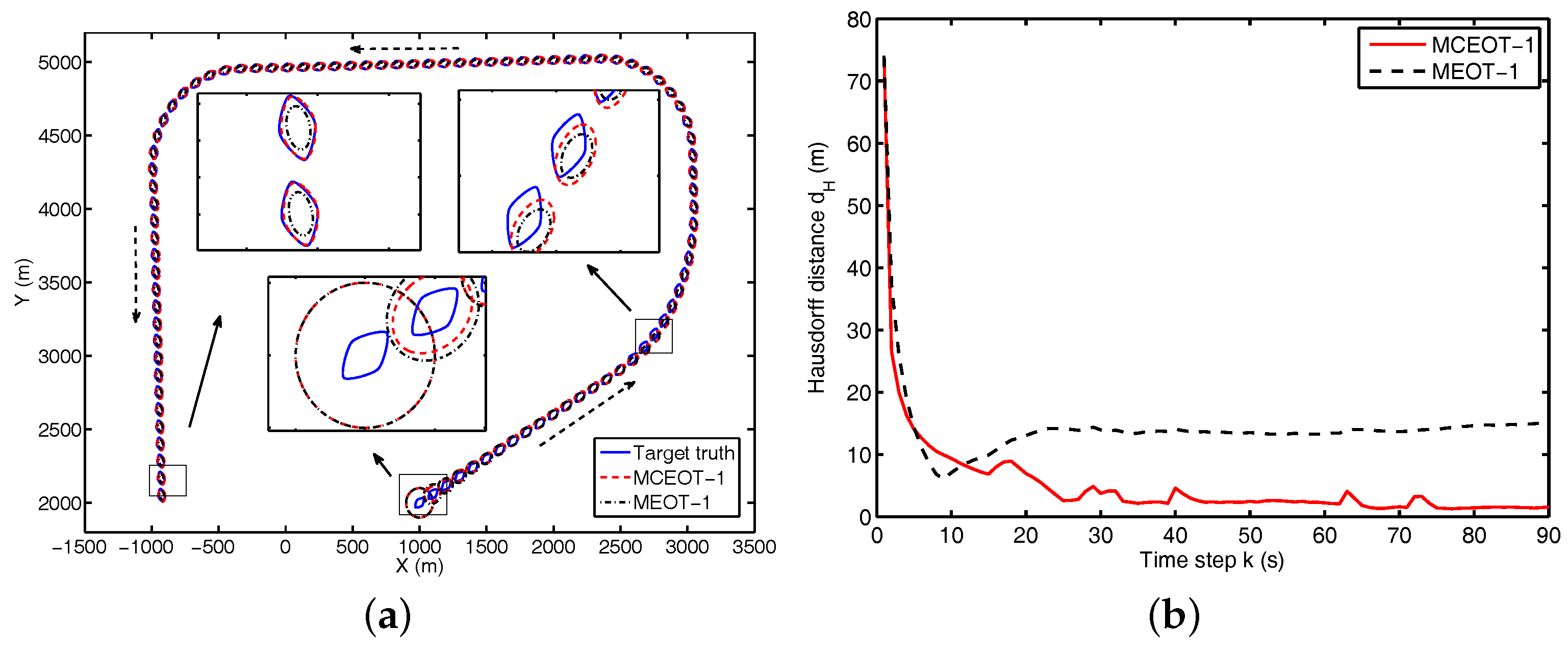
| MCOET-1 | MEOT-1 |
|---|---|
| 0.2971 | 0.1103 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Ji, B.; Lan, J.; He, Z.; Pu, J. Tracking of Maneuvering Complex Extended Object with Coupled Motion Kinematics and Extension Dynamics Using Range Extent Measurements. Sensors 2017, 17, 2184. https://doi.org/10.3390/s17102184
Sun L, Ji B, Lan J, He Z, Pu J. Tracking of Maneuvering Complex Extended Object with Coupled Motion Kinematics and Extension Dynamics Using Range Extent Measurements. Sensors. 2017; 17(10):2184. https://doi.org/10.3390/s17102184
Chicago/Turabian StyleSun, Lifan, Baofeng Ji, Jian Lan, Zishu He, and Jiexin Pu. 2017. "Tracking of Maneuvering Complex Extended Object with Coupled Motion Kinematics and Extension Dynamics Using Range Extent Measurements" Sensors 17, no. 10: 2184. https://doi.org/10.3390/s17102184




