Online Condition Monitoring of a Rail Fastening System on High-Speed Railways Based on Wavelet Packet Analysis
Abstract
:1. Introduction
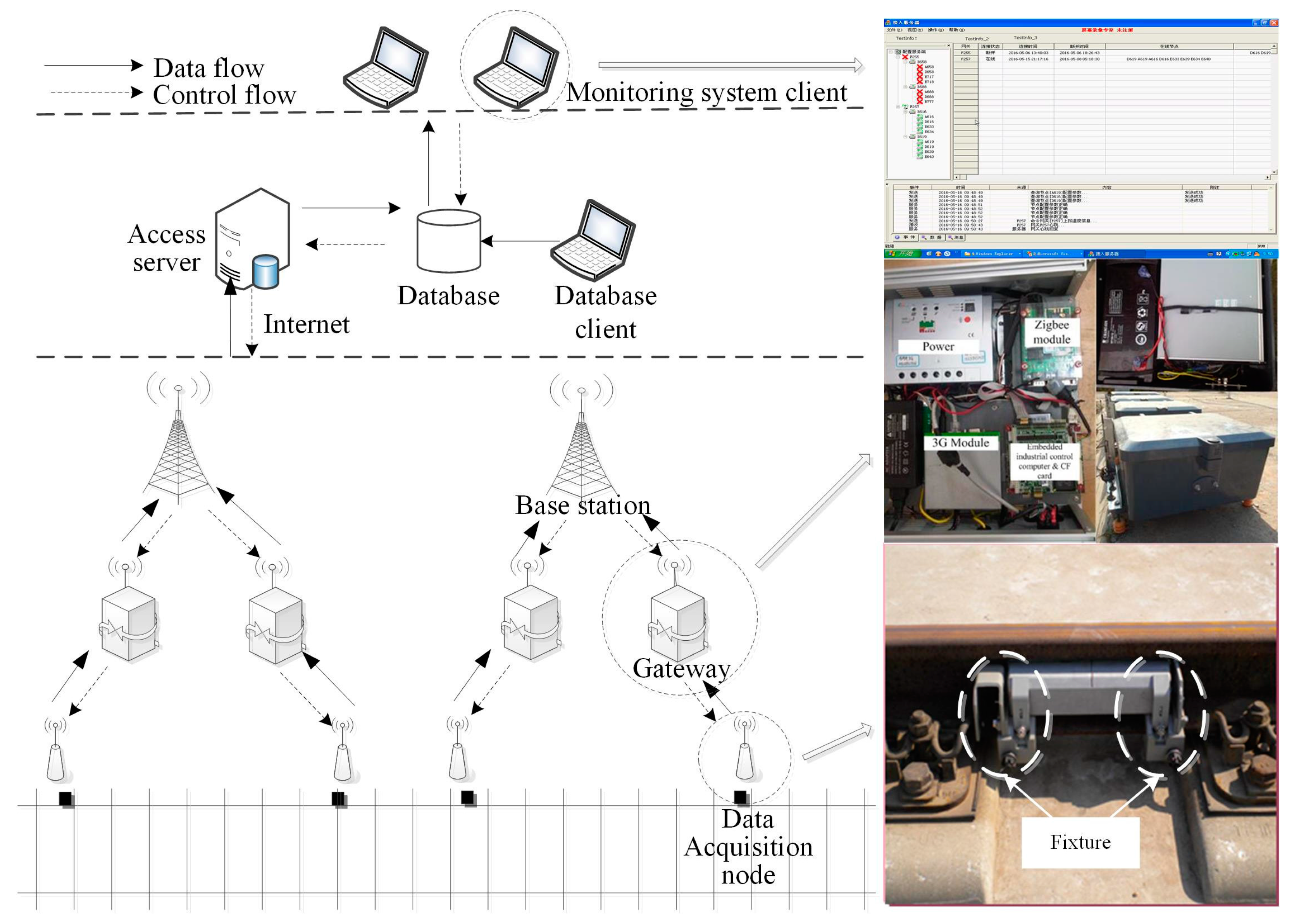
2. Monitoring System Overview
3. Materials and Methods
3.1. High-Speed Railway Experimental Platform
3.2. Wavelet Packet Theory
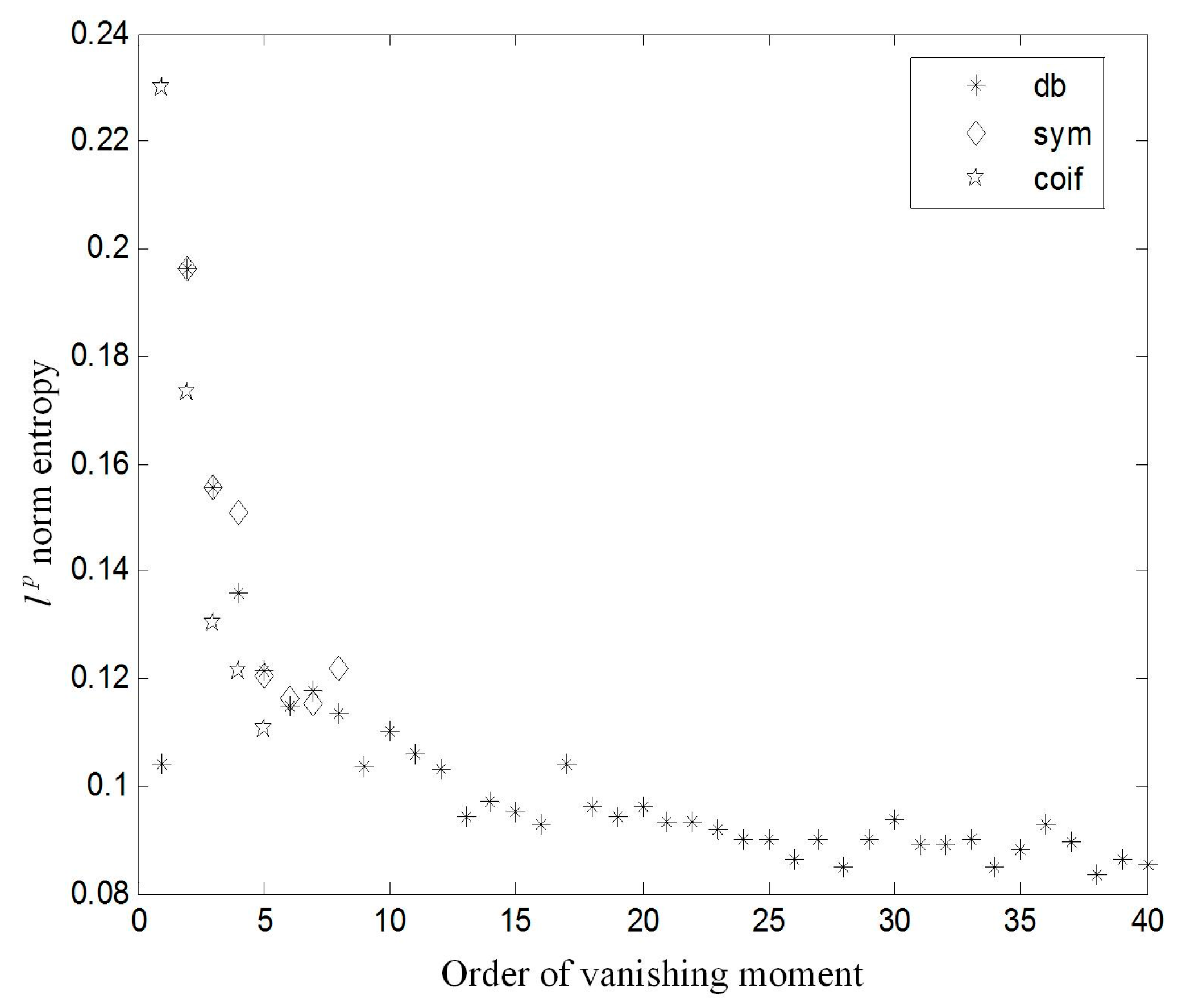
3.3. Choice of Wavelet Basis and the Level’s Number
3.4. Wavelet Packet Frequency Band Extraction
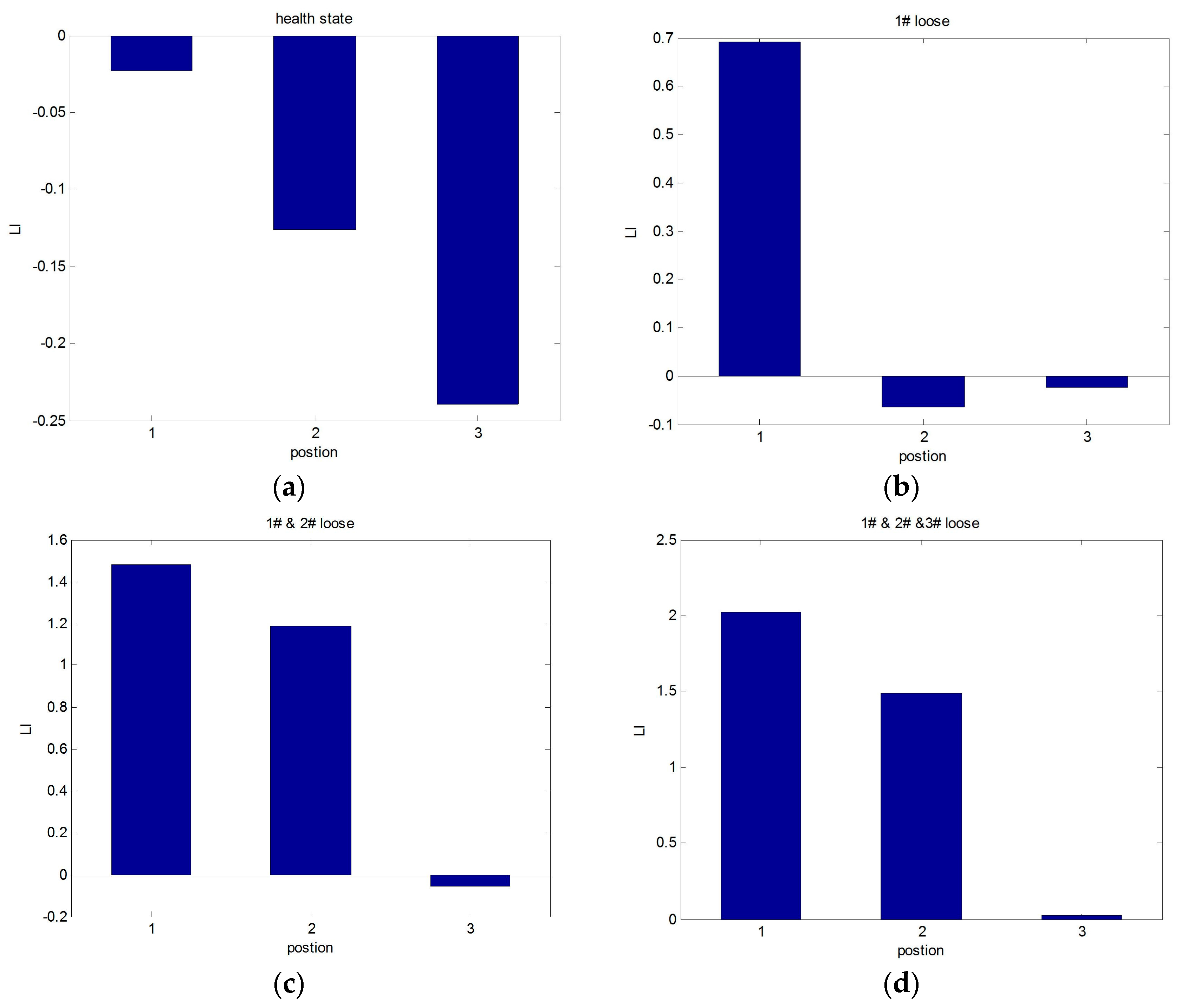
3.5. Damage Location Index Based on WPT
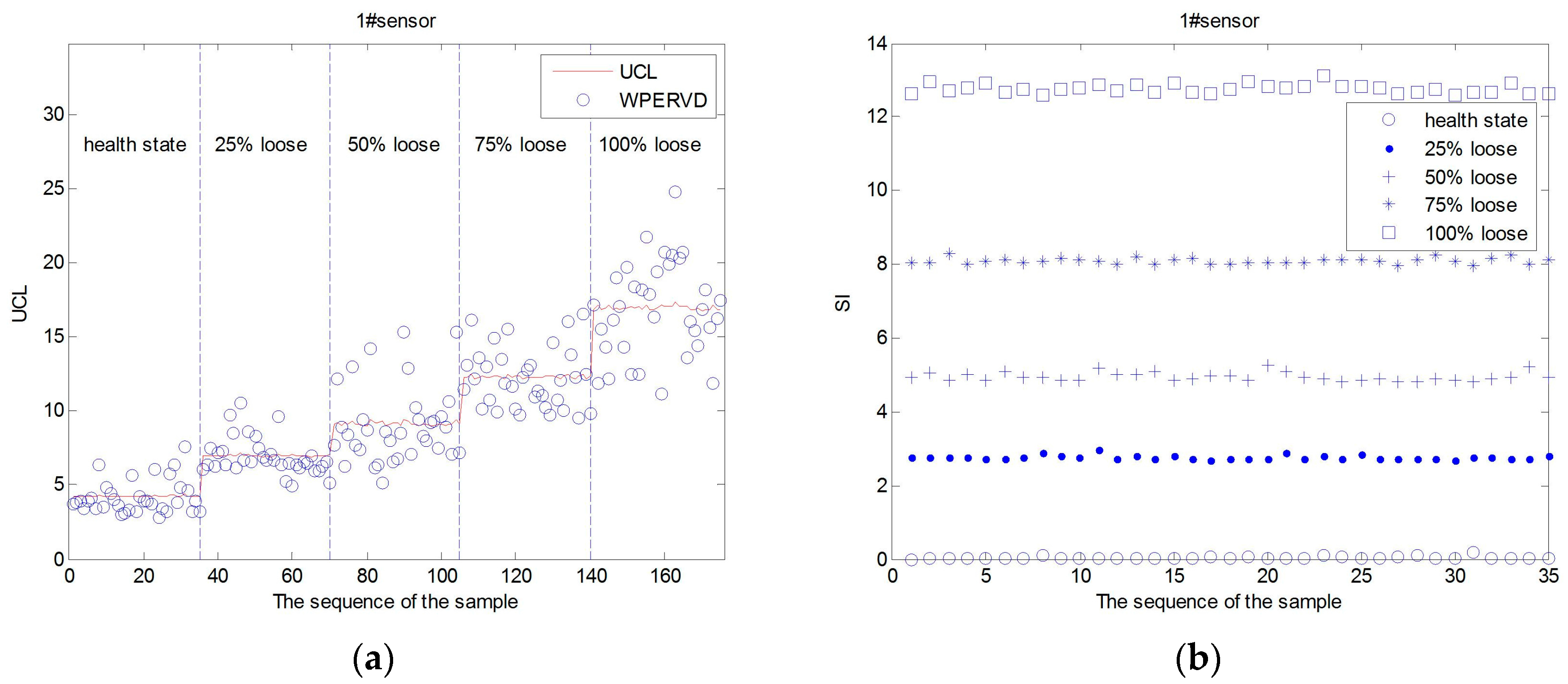
3.6. Damage Severity Index Based on WPT
4. Experimental Results
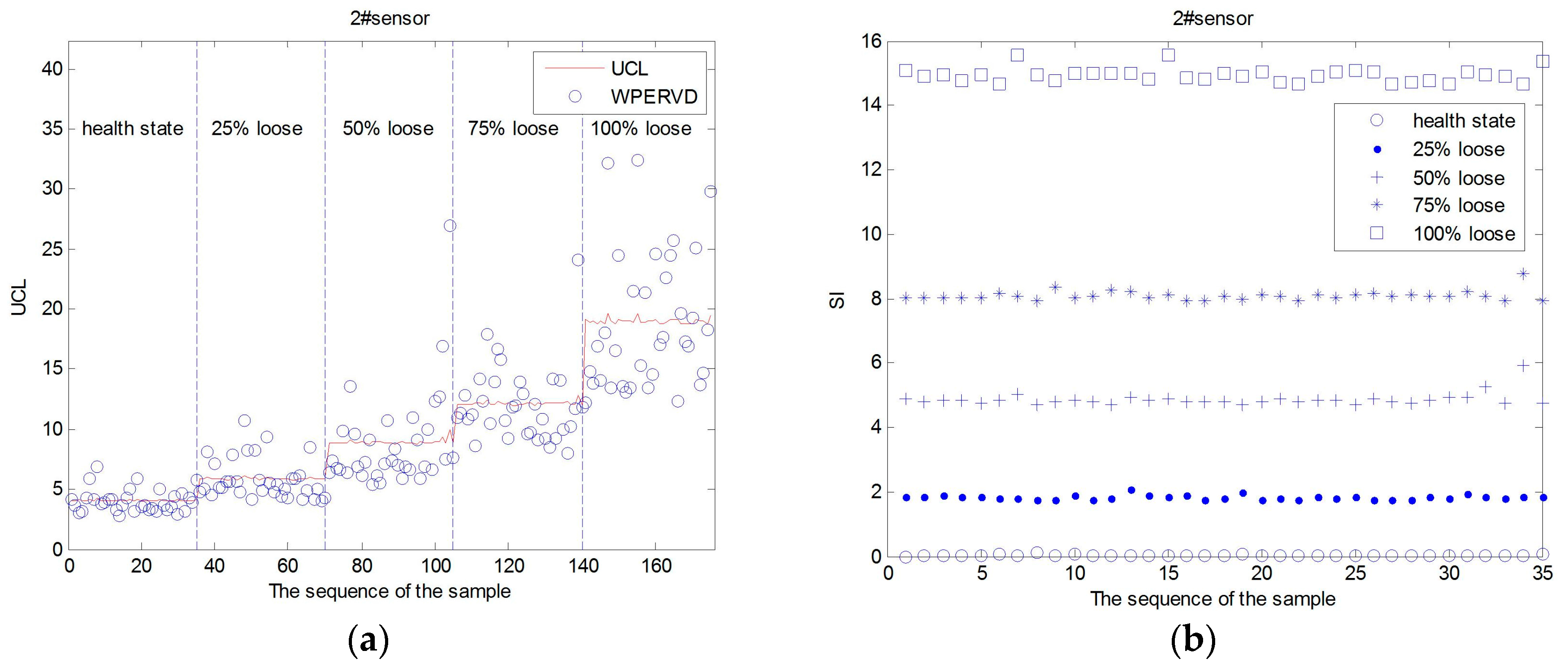
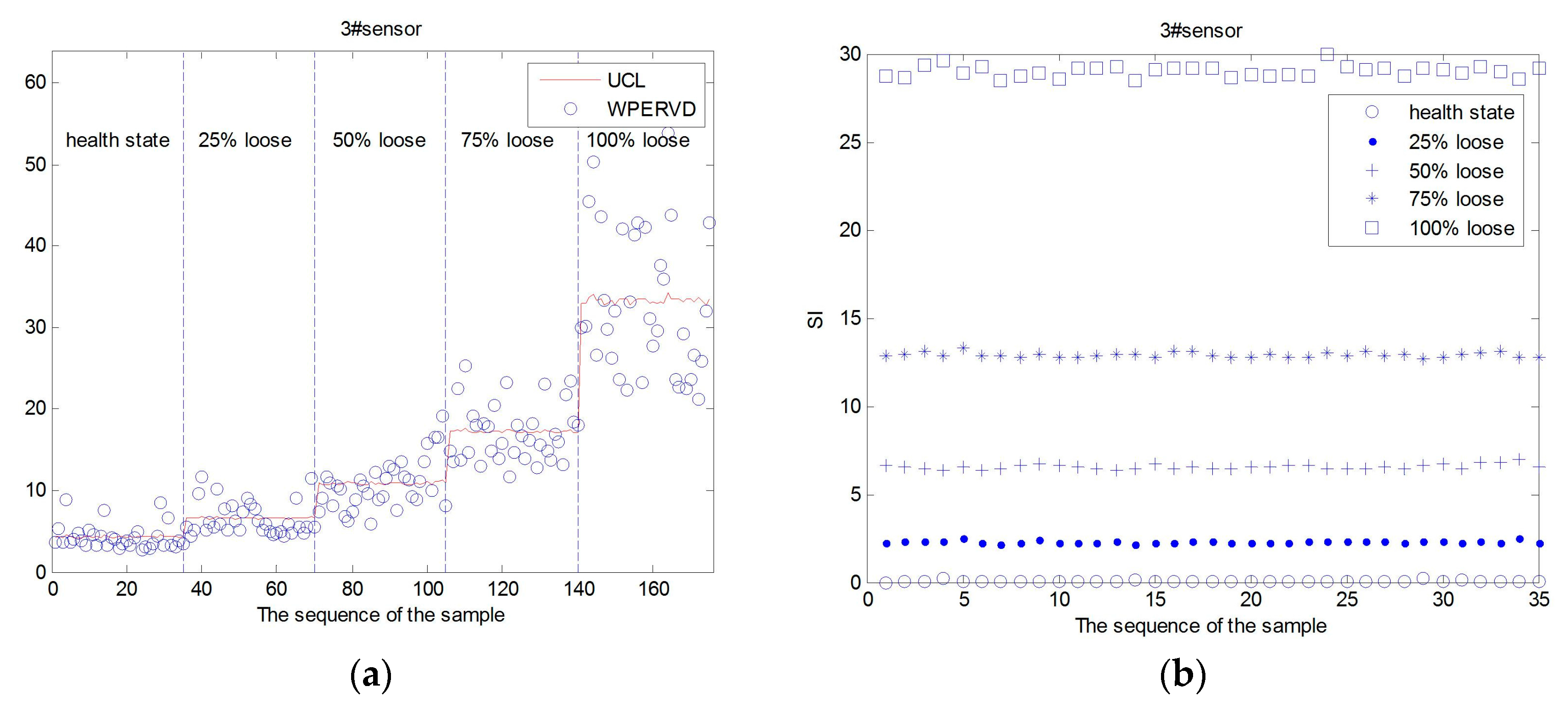
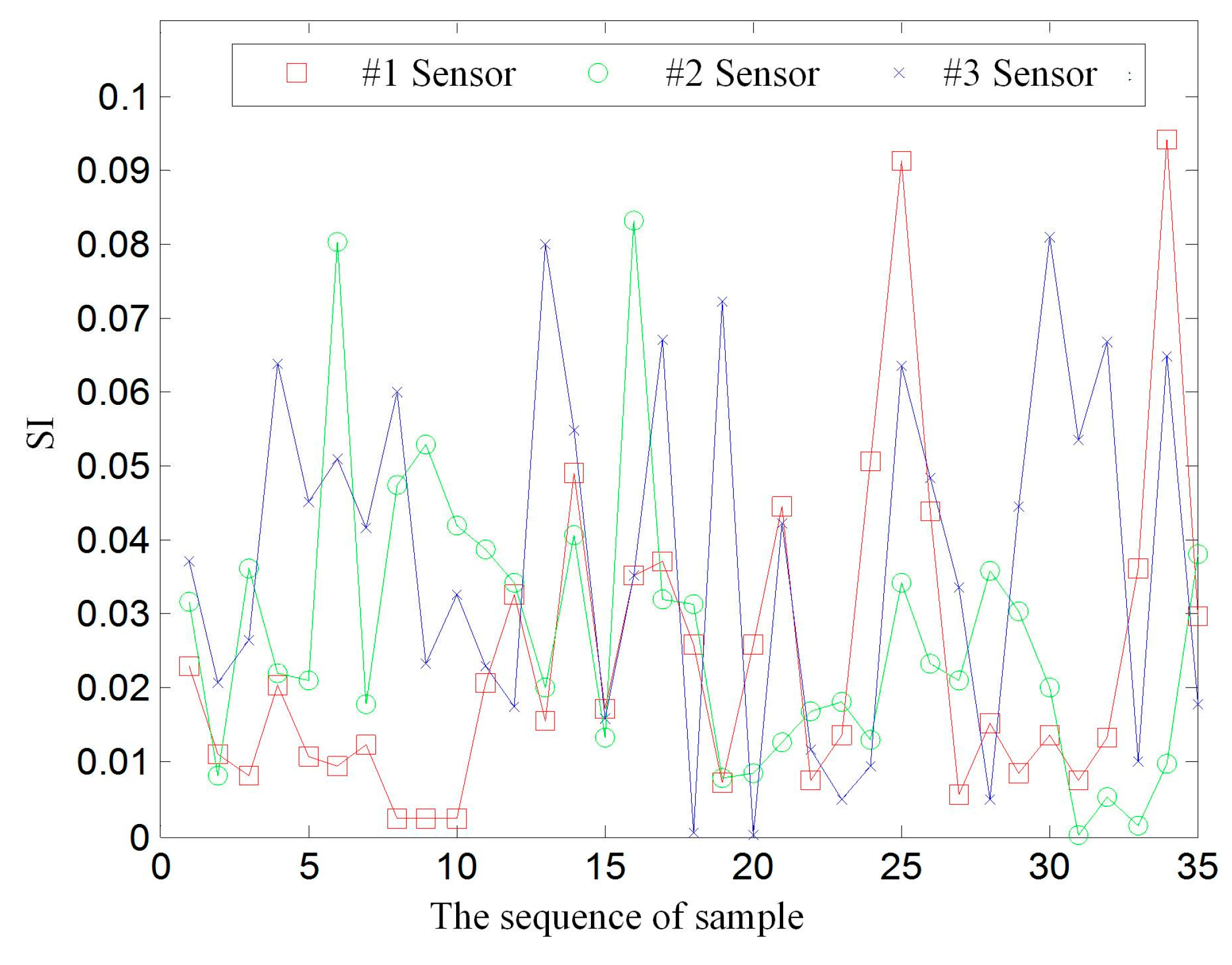
4.1. Damage Location Identification
4.2. Damage Severity Identification
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Diego, S.; Casado, J.A.; Carrascal, I.; Polanco, J.A.; Gutierrez-Solana, F. Experimental validation of an adjustable railway fastening for slab track. J. Test. Eval. 2010, 38, 1–11. [Google Scholar]
- Zhao, X.; Li, Z.L.; Dollevoet, R. Influence of the fastening modeling on the vehicle-track interaction at singular rail surface defects. J. Comput. Nonlinear Dyn. 2014, 9, 031002. [Google Scholar] [CrossRef]
- Anastasopoulos, I.; Gazetas, G. Analysis of failure of guardrail base-plates in scissors crossovers of the Athens Metro: The role of foundation-structure interaction. Eng. Fail. Anal. 2007, 14, 765–782. [Google Scholar] [CrossRef]
- Xiao, X.B.; Jin, X.S.; Wen, Z.F. Effect of disabled fastening systems and ballast on vehicle derailment. J. Vib. Acoust. 2007, 129, 217–229. [Google Scholar] [CrossRef]
- Mazzeo, P.L.; Nitti, M.; Stella, E.; Distante, A. Visual recognition of fastening bolts for railroad maintenance. Pattern Recogn. Lett. 2004, 25, 669–677. [Google Scholar] [CrossRef]
- Marino, F.; Distante, A.; Mazzeo, P.L.; Stella, E. A real-time visual inspection system for railway maintenance: Automatic hexagonal-headed bolts detection. IEEE Trans. Syst. Man Cybern. C 2007, 37, 418–428. [Google Scholar] [CrossRef]
- Aytekin, C.; Rezaeitabar, Y.; Dogru, S.; Ulusoy, I. Railway fastener inspection by real-time machine vision. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 1101–1107. [Google Scholar] [CrossRef]
- Yang, J.; Tao, W.; Liu, M.; Zhang, H.; Zhao, H. An efficient direction field-based method for the detection of fasteners on high-speed railways. Sensors 2011, 11, 7364–7381. [Google Scholar] [CrossRef] [PubMed]
- Feng, H.; Jiang, Z.; Xie, F.; Yang, P.; Shi, J. Automatic fastener classification and defect detection in vision-based railway inspection systems. IEEE Trans. Instrum. Meas. 2014, 63, 877–888. [Google Scholar] [CrossRef]
- Zhao, J.J.; Zhao, X.B.; Li, X.H.; Zhang, B.; Wang, B.; Zhang, W. Fasteners state detection system based on wireless data transfer module. Appl. Mech. Mater. 2014, 513, 3924–3927. [Google Scholar] [CrossRef]
- Fan, W.; Qiao, P. Vibration-based damage identification methods: A review and comparative study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Farrar, C.R.; Doebling, S.W.; Nix, D.A. Vibration-based structural damage identification. Struct. Health Monit. 2001, 359, 131–149. [Google Scholar] [CrossRef]
- Wang, W.J.; Zhang, J.; Li, X.H. Rail fastener looseness detection. Noise Vib. Control 2013, 33, 151–154. [Google Scholar]
- Ren, T.; He, L.; Wang, D.; Liang, J.; Hui, M. Structural state detection using quaternion-based three-channel joint transmissibility. J. Vibroeng. 2015, 17, 928–938. [Google Scholar]
- Liu, C.; Zhang, L.H.; Ren, T.Q.; Liang, J.S.; Wang, D.Z.; Wang, K.; Wang, T.R. Detection of rail fastener conditions using time-frequency entropy based on orthogonal empirical mode decomposition. Appl. Mech. Mater. 2013, 333–335, 1708–1712. [Google Scholar] [CrossRef]
- Oregui, M.; Li, S.; Núñez, A.; Carroll, R.; Dollevoet, R. Monitoring bolt tightness of rail joints using axle box acceleration measurements. Struct. Control Health Monit. 2016. [Google Scholar] [CrossRef]
- Ding, Y.L.; Li, A.Q.; Miao, C.Q. Theoretical research on structural damage alarming of long-span bridges using wavelet packet analysis. J. Southeast Univ. (Engl. Ed.) 2005, 21, 459–462. [Google Scholar]
- Liu, C.; Wei, J.H.; Zhang, Z.X.; Liang, J.S.; Ren, T.Q.; Xu, H.Q. Design and evaluation of a remote measurement system for the online monitoring of rail vibration signals. Proc. Inst. Mech. Eng. F 2016, 230, 724–733. [Google Scholar]
- Oregui, M.; Molodova, M.; Núñez, A.; Dollevoet, R.; Li, Z. Experimental investigation into the condition of insulated rail joints by impact excitation. Exp. Mech. 2015, 55, 1597–1612. [Google Scholar] [CrossRef]
- Oregui, M.; Li, Z.; Dollevoet, R. An investigation into the vertical dynamics of tracks with monoblock sleepers with a 3D finite-element model. Proc. Inst. Mech. Eng. F 2016, 230, 891–908. [Google Scholar] [CrossRef]
- Ravanfar, S.A.; Razak, H.A.; Ismail, Z.; Monajemi, H. An improved method of parameter identification and damage detection in beam structures under flexural vibration using wavelet multi-resolution analysis. Sensors 2015, 15, 22750–22775. [Google Scholar] [CrossRef] [PubMed]
- Shao, R.; Hu, W.; Wang, Y.; Qi, X. The fault feature extraction and classification of gear using principal component analysis and kernel principal component analysis based on the wavelet packet transform. Measurement 2014, 54, 118–132. [Google Scholar] [CrossRef]
- Poornachandra, S. Wavelet-based denoising using subband dependent threshold for ECG signals. Digit. Signal Process. 2008, 18, 49–55. [Google Scholar] [CrossRef]
- To, A.C.; Moore, J.R.; Glaser, S.D. Wavelet denoising techniques with applications to experimental geophysical data. Signal Process. 2008, 89, 144–160. [Google Scholar] [CrossRef]
- Parameswariah, C.; Cox, M. Frequency characteristics of wavelets. IEEE Power Eng. Rev. 2002, 17, 800–804. [Google Scholar]



| Decomposition Level | Cost Function | Computation Time (s) |
|---|---|---|
| 1 | 3.085 | 0.055 |
| 2 | 1.861 | 0.056 |
| 3 | 1.492 | 0.063 |
| 4 | 0.938 | 0.075 |
| 5 | 0.589 | 0.102 |
| 6 | 0.307 | 0.172 |
| 7 | 0.159 | 0.291 |
| 8 | 0.085 | 0.600 |
| 9 | 0.046 | 1.375 |
| 10 | 0.030 | 3.504 |
| 11 | 0.027 | 9.892 |
| 12 | 0.018 | 31.135 |
| Operating Condition | m = 128 | m = 154 | m = 180 | m = 192 |
|---|---|---|---|---|
| 1 | 0.732 | 0.749 | 0.808 | 0.877 |
| 2 | 0.740 | 0.760 | 0.783 | 0.886 |
| 3 | 0.718 | 0.738 | 0.826 | 0.864 |
| 4 | 0.718 | 0.747 | 0.819 | 0.871 |
| 5 | 0.712 | 0.743 | 0.797 | 0.871 |
| Serial Number | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Number of loose fasteners | 0 | 1 | 2 | 3 |
| Location of loose fasteners | Null | #1 | #1 and #2 | #1 and #2 and #3 |
| Serial Number | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Tightening torque (N·m) | 140 | 105 | 70 | 35 | 0 |
| Damage severity (%) | Null | 25 | 50 | 75 | 100 |
| Serial Number | SI | Calculated Looseness Degree (%) | Actual Looseness Degree (%) | Relative Error (%) |
|---|---|---|---|---|
| 1 | 2.241 | 24.960 | 25 | 0.160 |
| 2 | 2.221 | 24.816 | 25 | 0.736 |
| 3 | 6.431 | 50.434 | 50 | 0.868 |
| 4 | 6.394 | 50.241 | 50 | 0.482 |
| 5 | 13.245 | 74.835 | 75 | 0.220 |
| 6 | 13.211 | 74.752 | 75 | 0.331 |
| 7 | 30.159 | 99.879 | 100 | 0.121 |
| 8 | 30.581 | 100.285 | 100 | 0.285 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, J.; Liu, C.; Ren, T.; Liu, H.; Zhou, W. Online Condition Monitoring of a Rail Fastening System on High-Speed Railways Based on Wavelet Packet Analysis. Sensors 2017, 17, 318. https://doi.org/10.3390/s17020318
Wei J, Liu C, Ren T, Liu H, Zhou W. Online Condition Monitoring of a Rail Fastening System on High-Speed Railways Based on Wavelet Packet Analysis. Sensors. 2017; 17(2):318. https://doi.org/10.3390/s17020318
Chicago/Turabian StyleWei, Jiahong, Chong Liu, Tongqun Ren, Haixia Liu, and Wenjing Zhou. 2017. "Online Condition Monitoring of a Rail Fastening System on High-Speed Railways Based on Wavelet Packet Analysis" Sensors 17, no. 2: 318. https://doi.org/10.3390/s17020318
APA StyleWei, J., Liu, C., Ren, T., Liu, H., & Zhou, W. (2017). Online Condition Monitoring of a Rail Fastening System on High-Speed Railways Based on Wavelet Packet Analysis. Sensors, 17(2), 318. https://doi.org/10.3390/s17020318






