Intelligent Diagnosis Method for Rotating Machinery Using Dictionary Learning and Singular Value Decomposition
Abstract
:1. Introduction
2. Dictionary Learning Scheme
2.1. Sparse Representation Theory
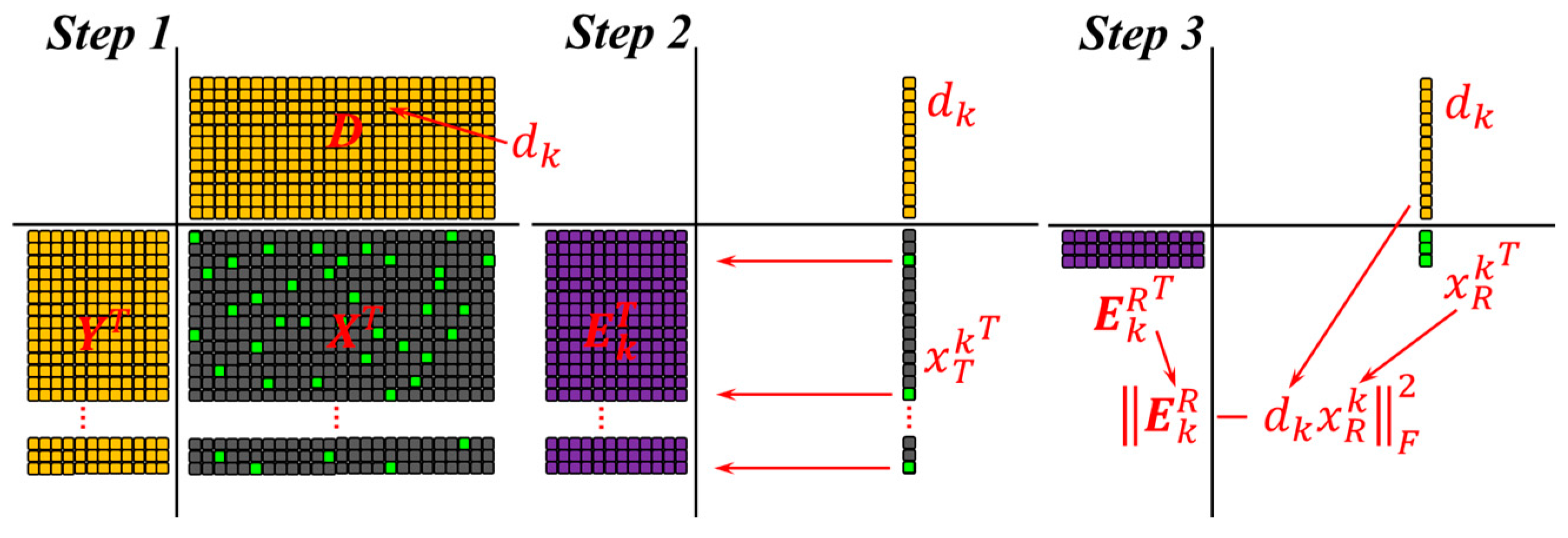
2.2. K-SVD Dictionary Learning
3. Singular Value Decomposition
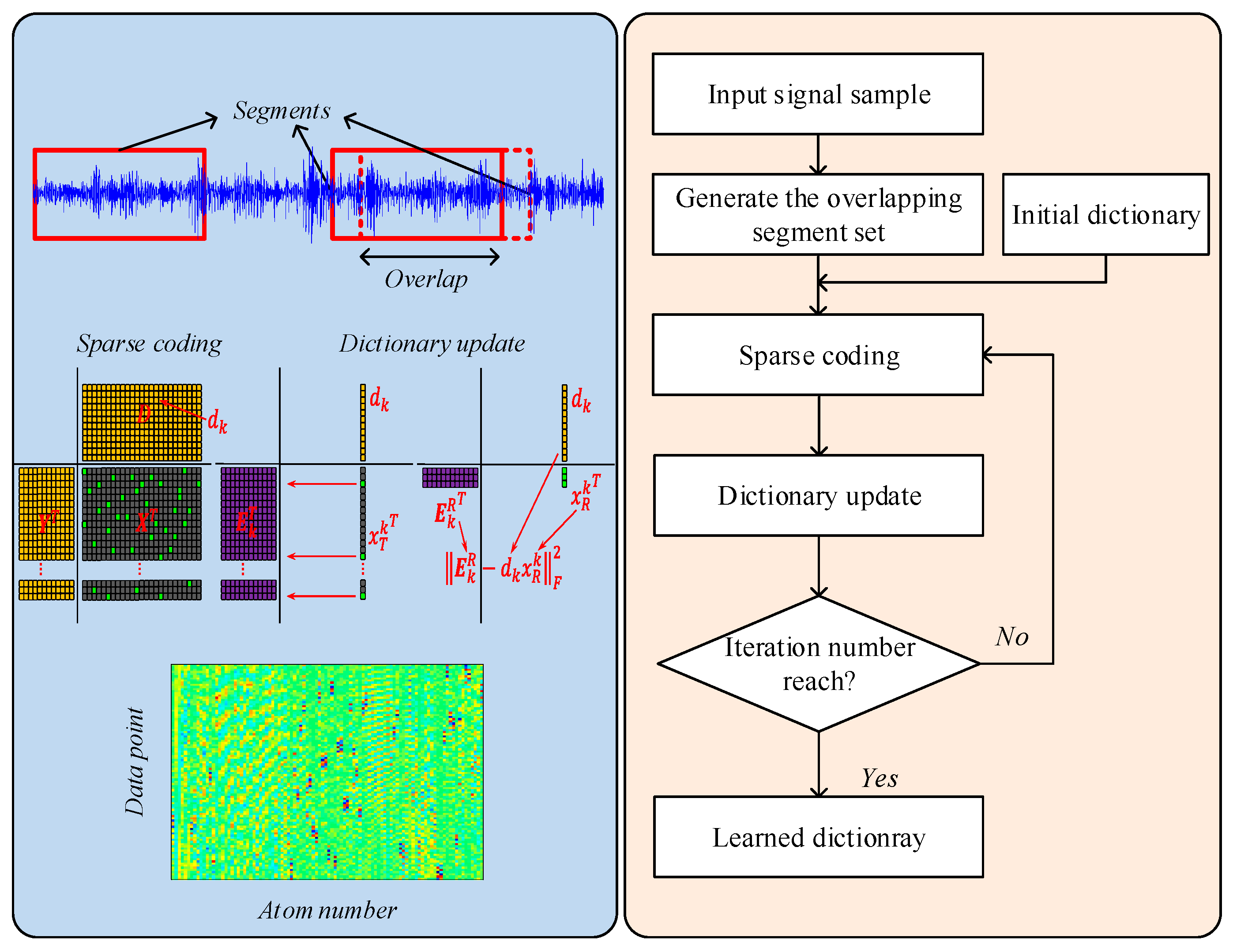
4. Proposed Method
- (1).
- Given a signal sample, partition the signal into an amount of overlapping segments and generate the dataset for dictionary learning.
- (2).
- Set the initial parameters, i.e., initial dictionary , iteration number , noise level .
- (3).
- Sparse coding: use the OMP algorithm in Section 2.1 to find the sparse representation coefficient.
- (4).
- Dictionary update: update the atoms in the dictionary according to the learning algorithm in Section 2.2.
- (5).
- Repeat the step (3) and (4) until the number of iteration reach.
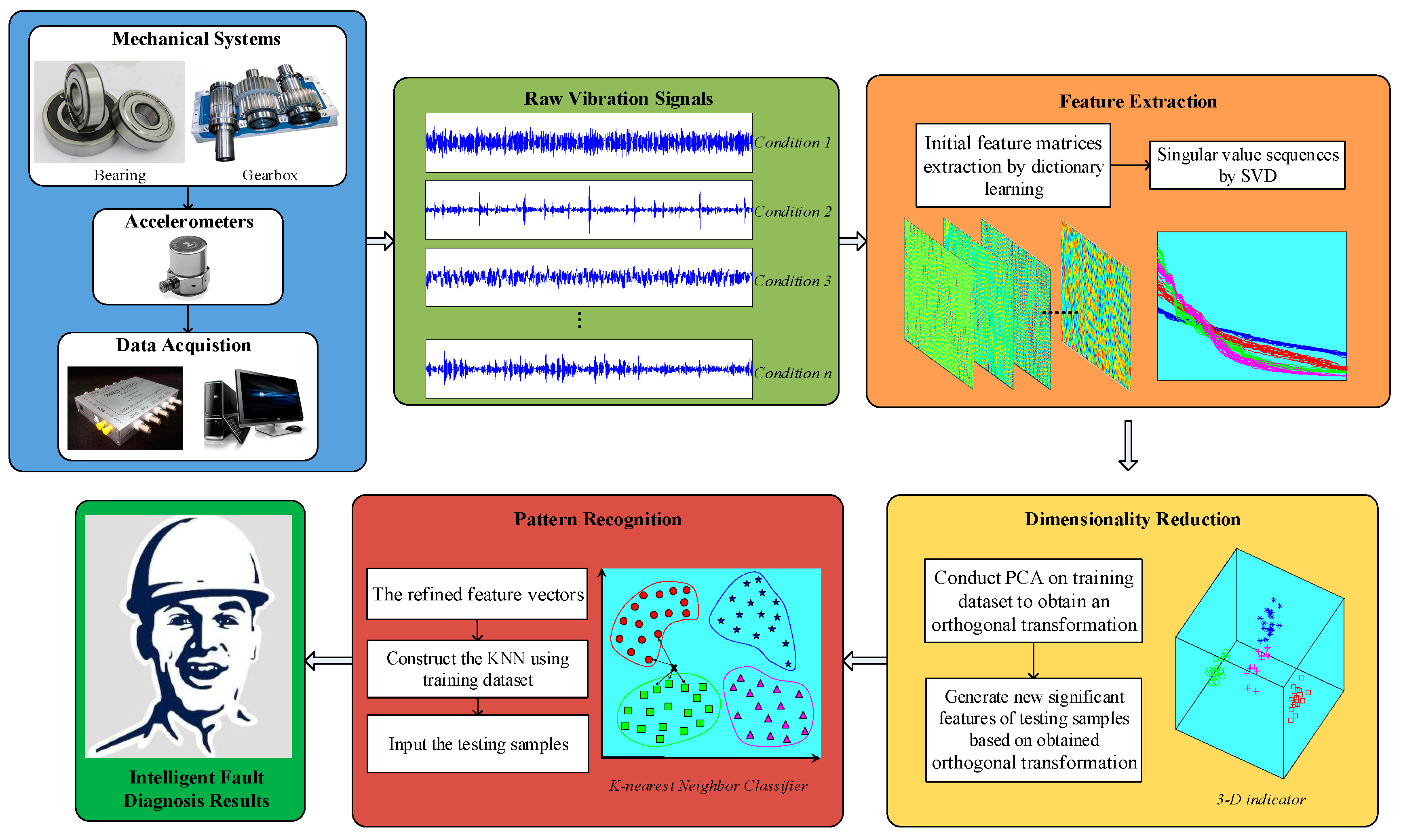
5. Experimental Results and Comparisons
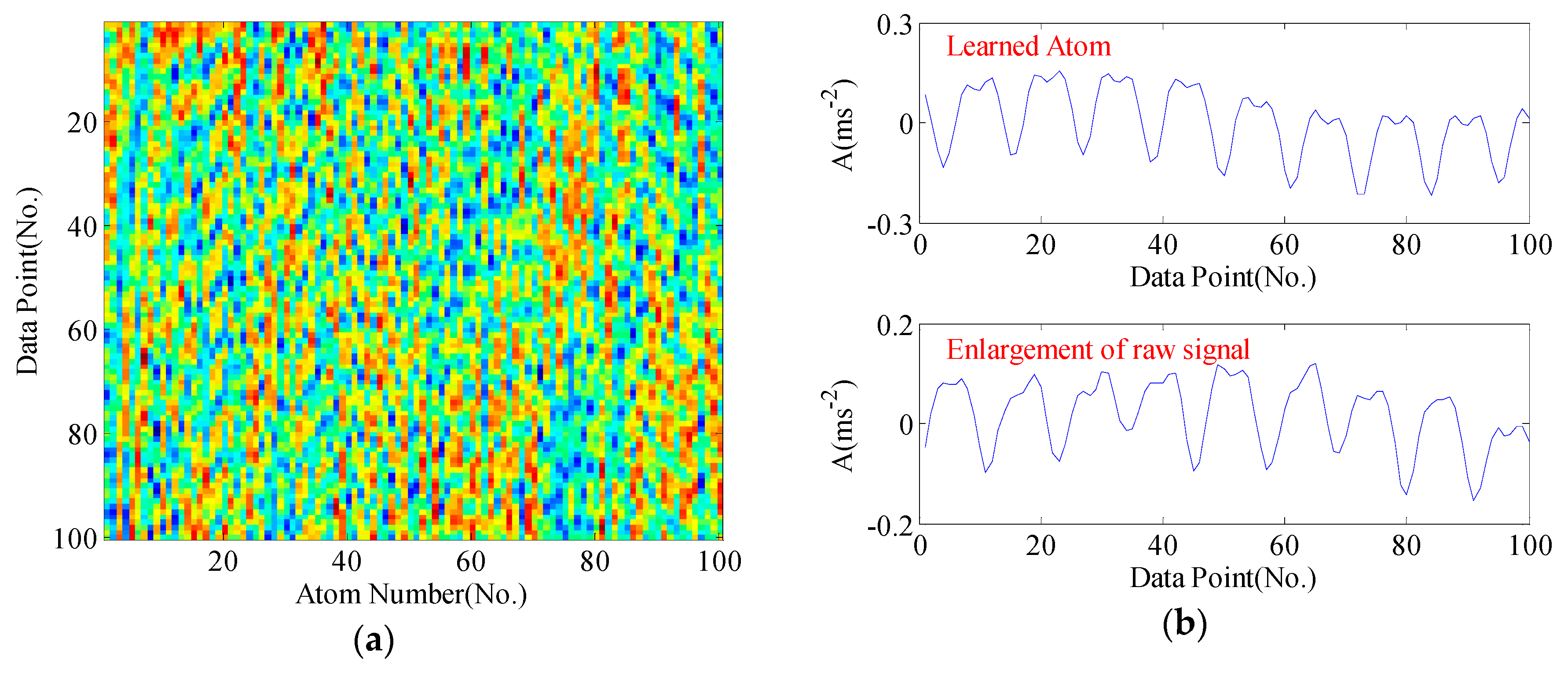
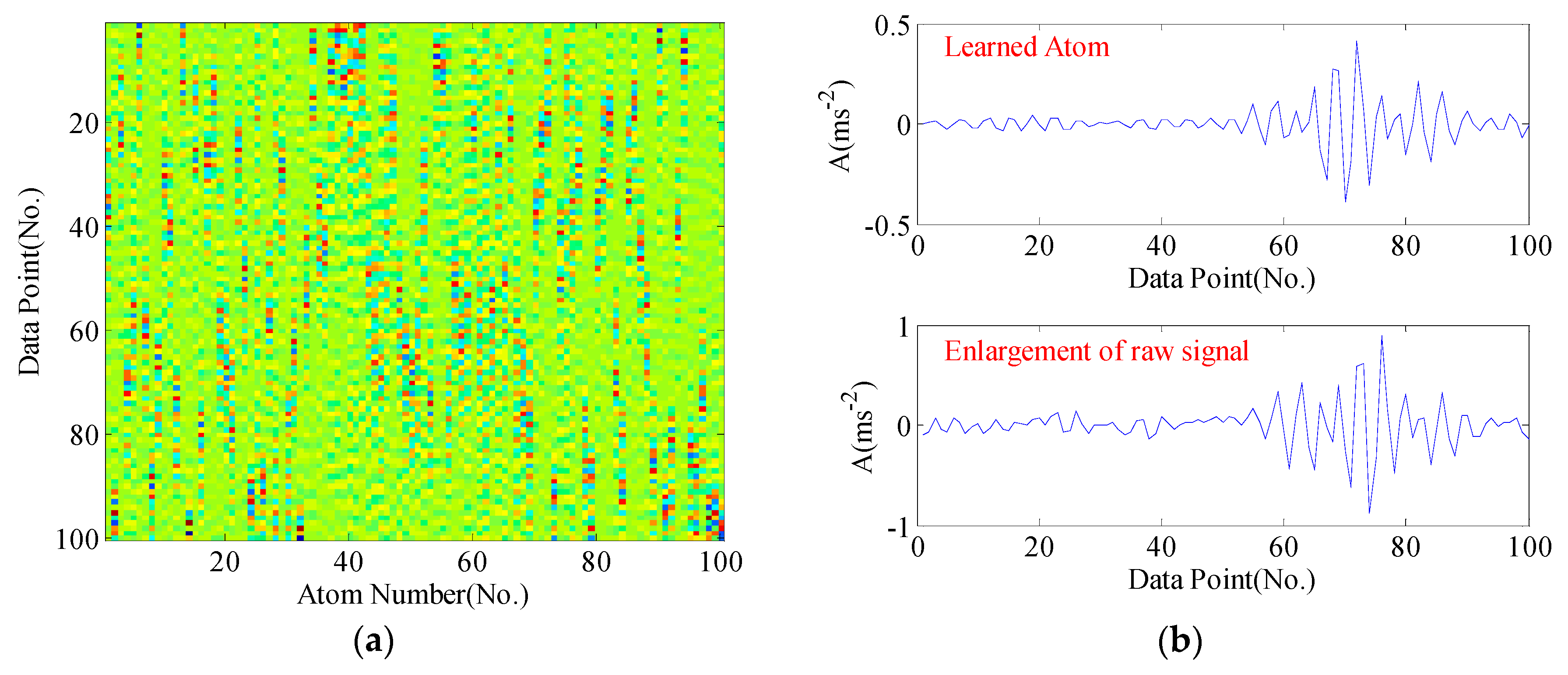
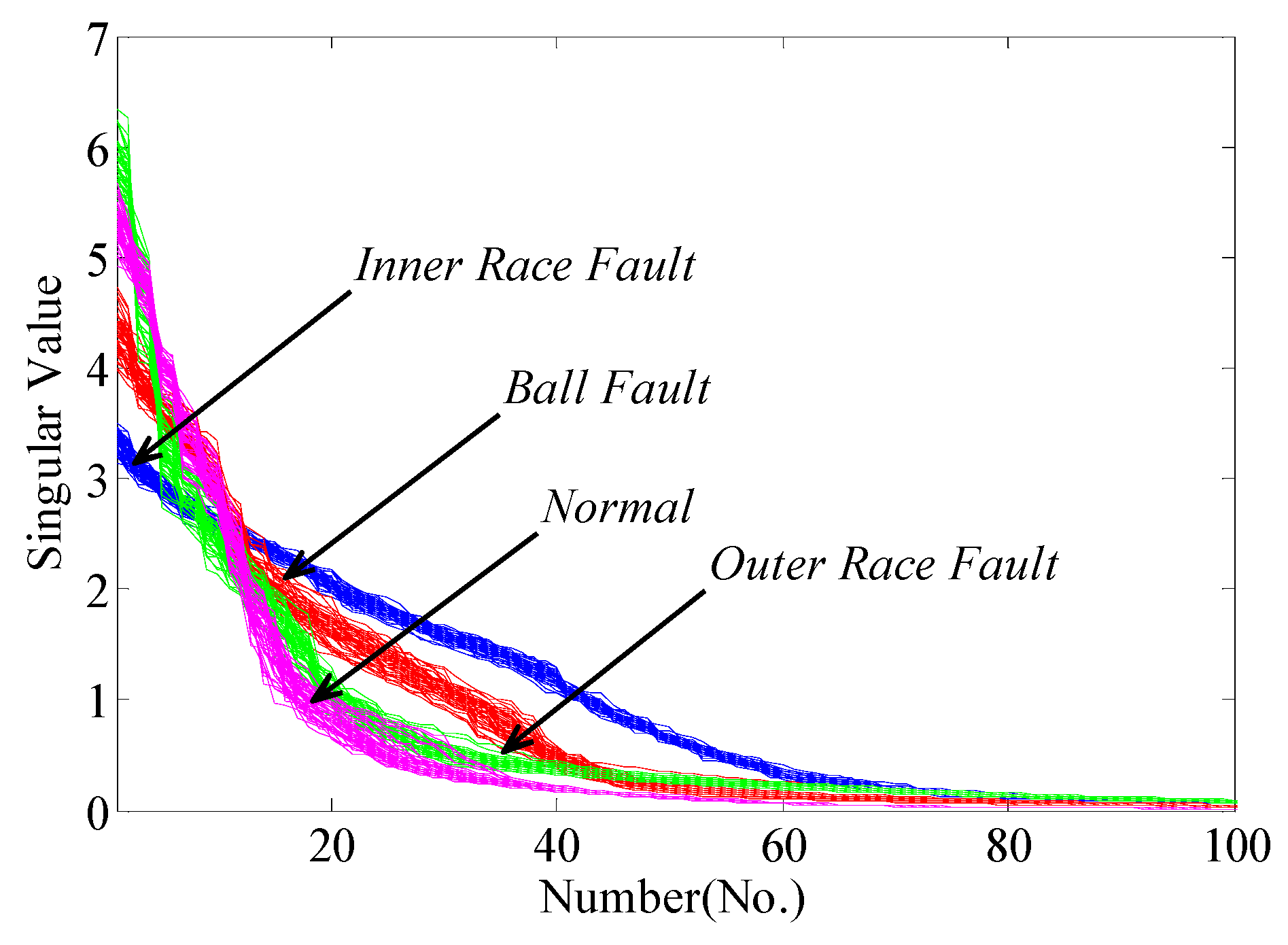
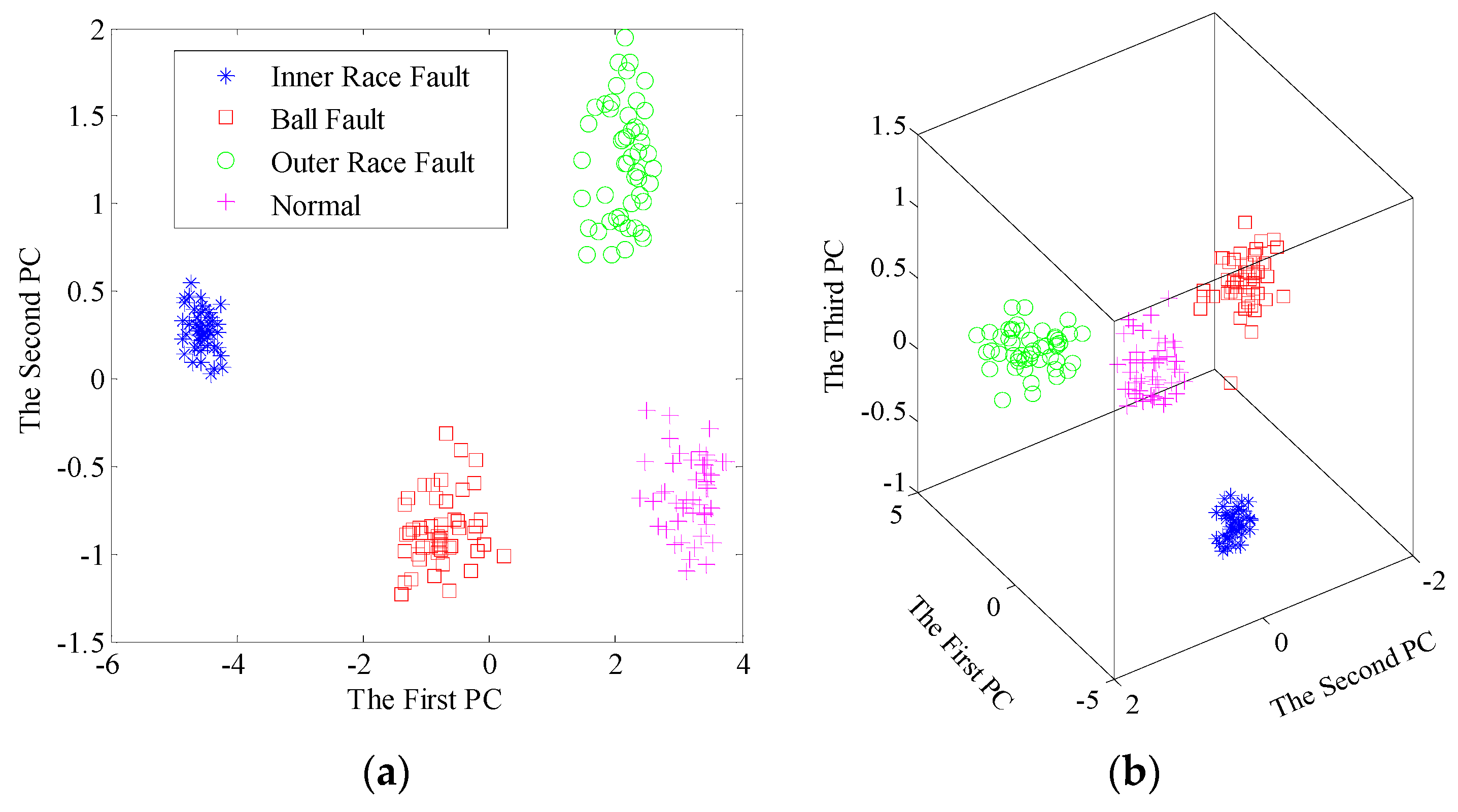
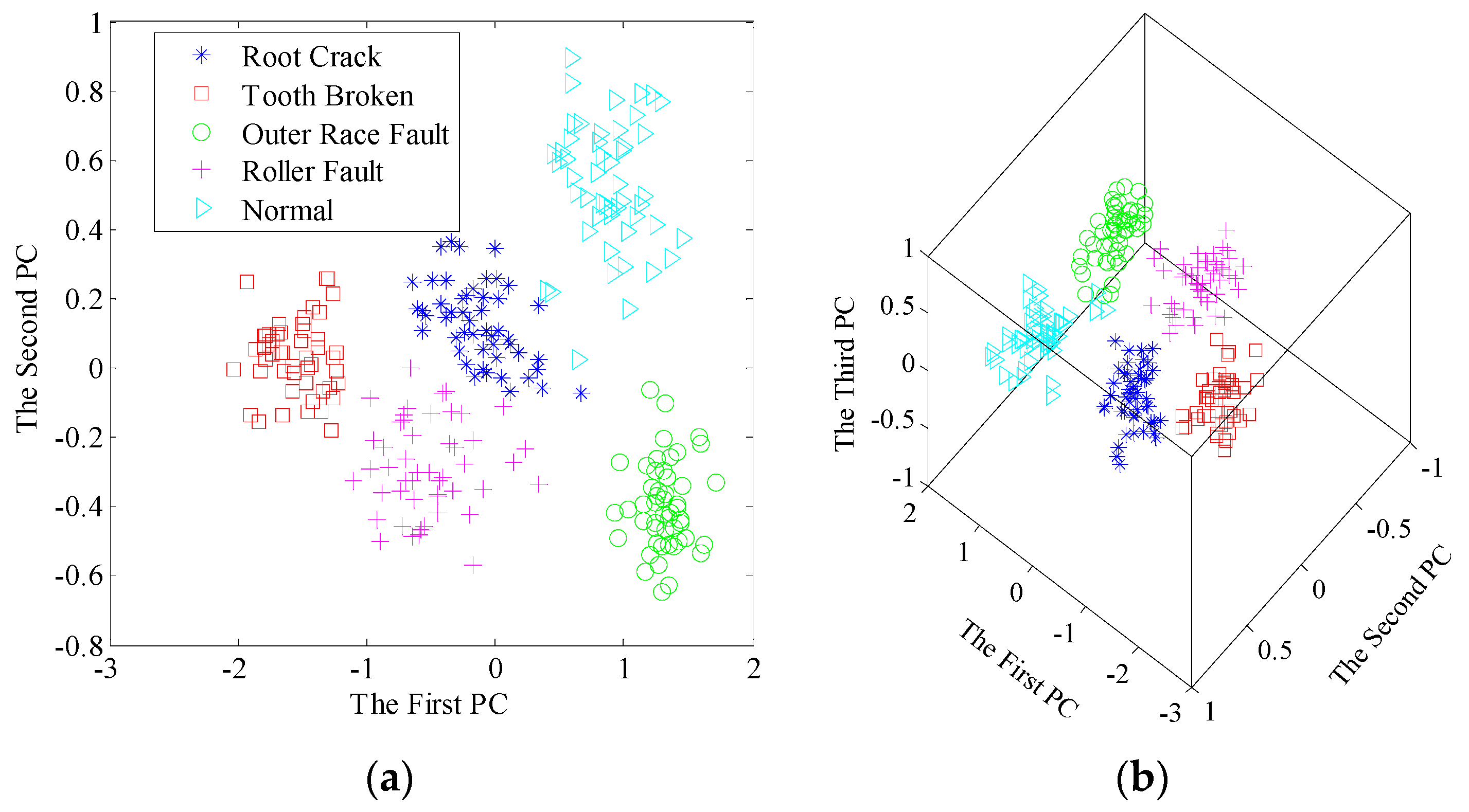
5.1. Case 1: Rolling Bearing Fault Diagnosis
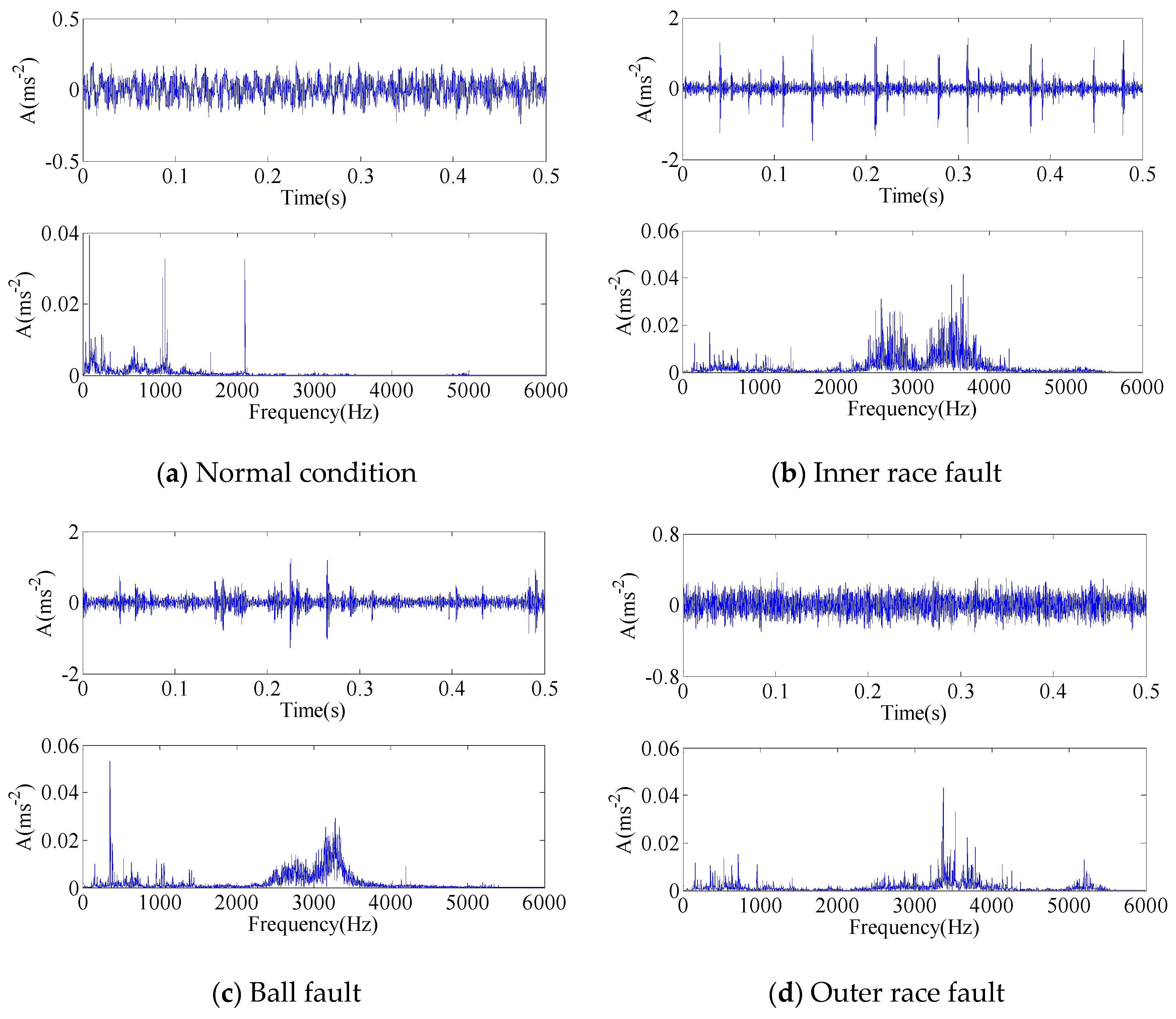
5.1.1. Experimental Data
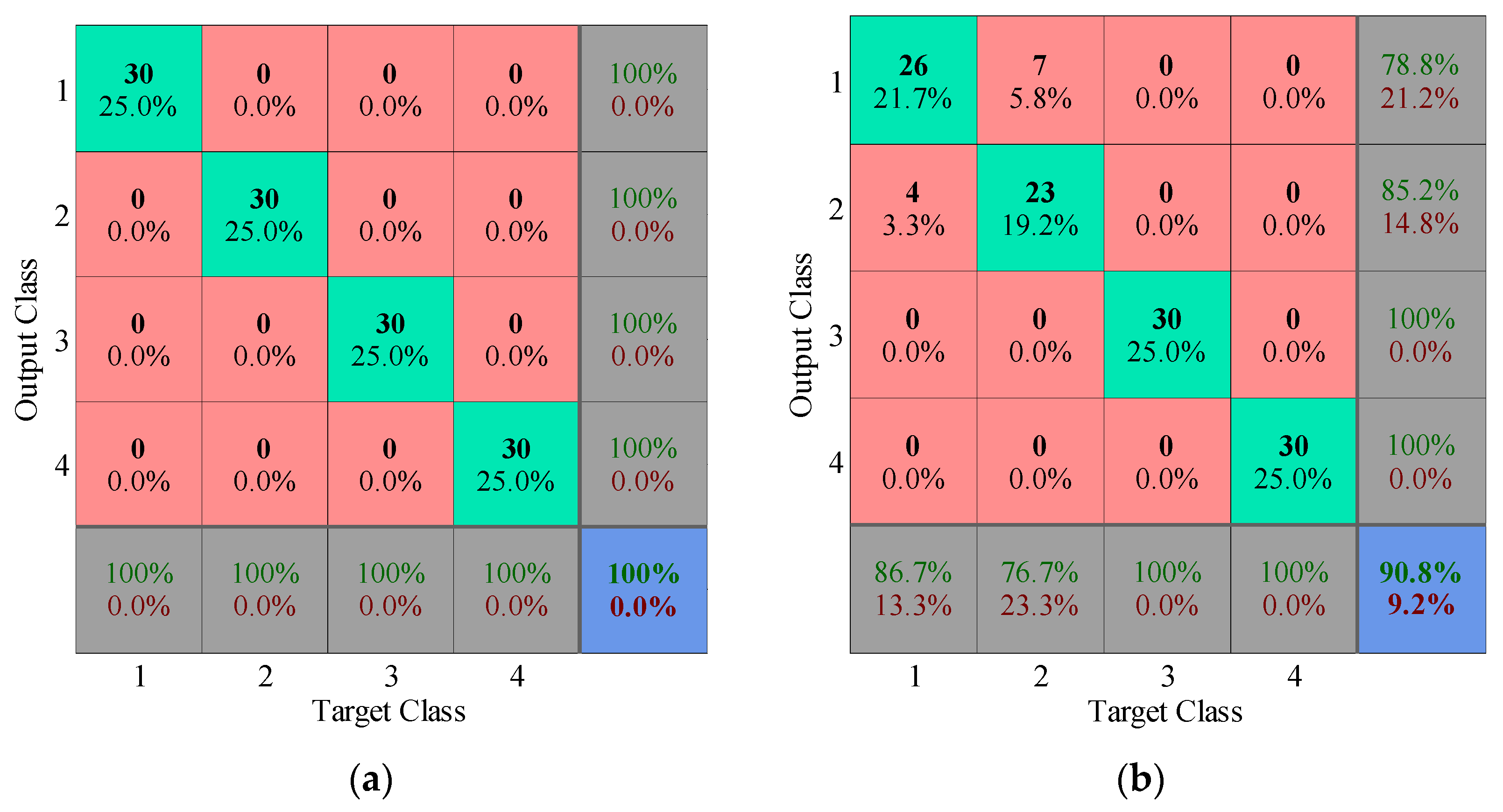
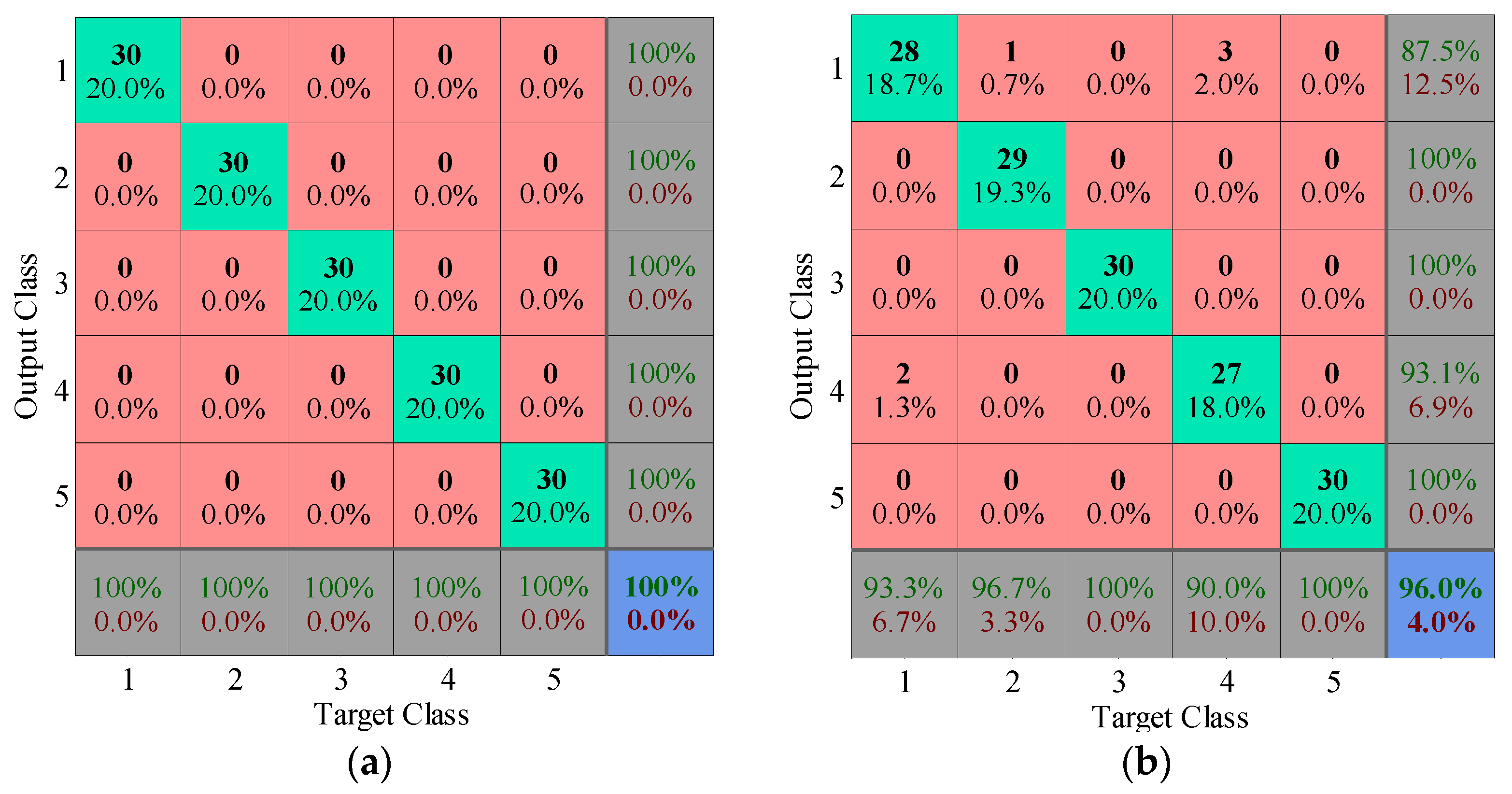
5.1.2. Diagnosis Procedure and Results
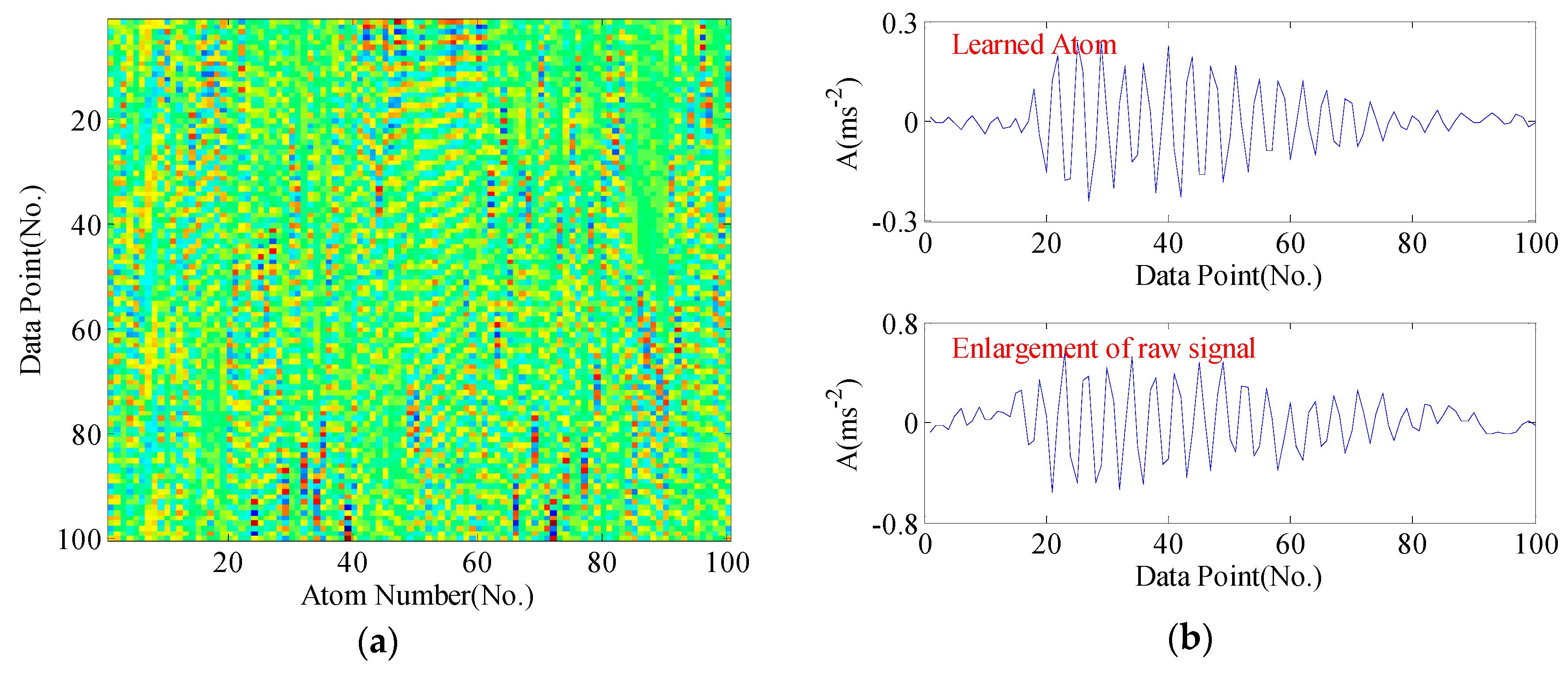
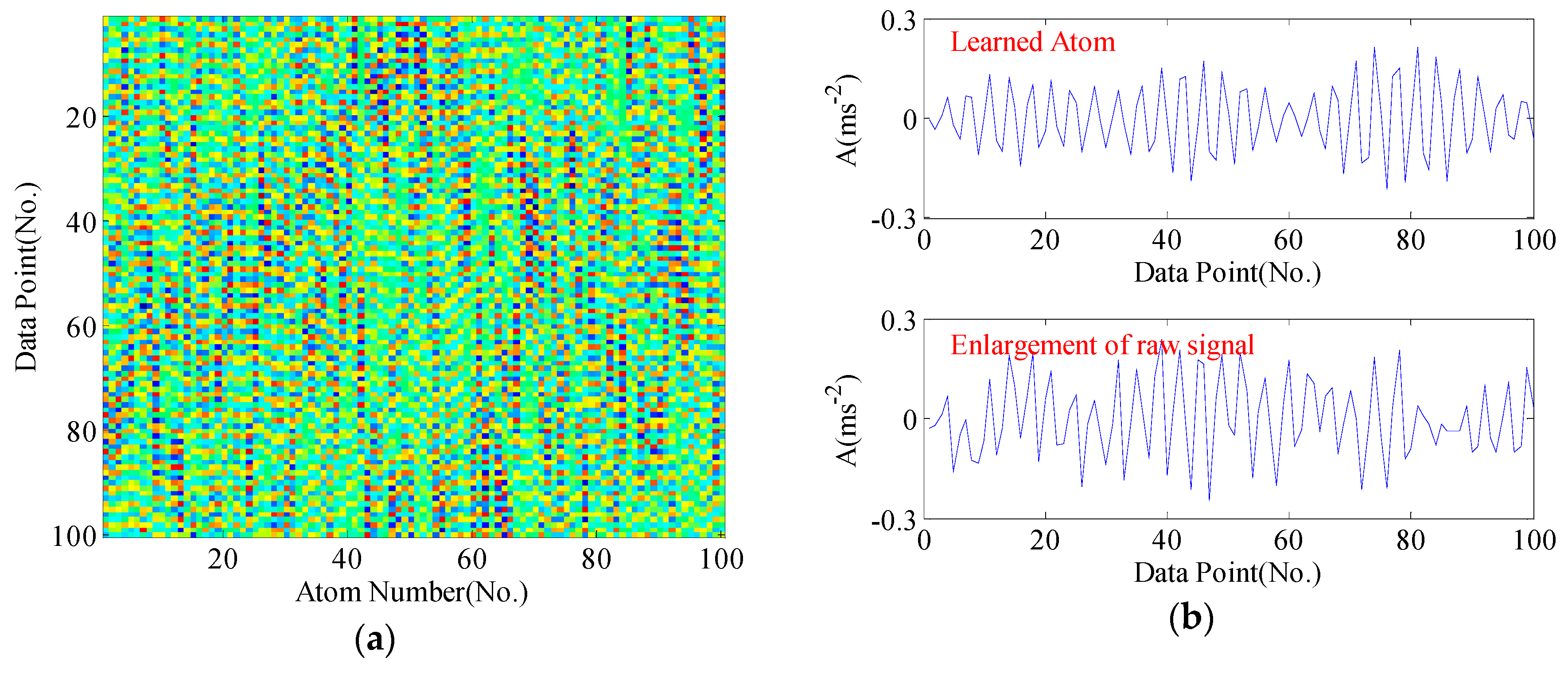
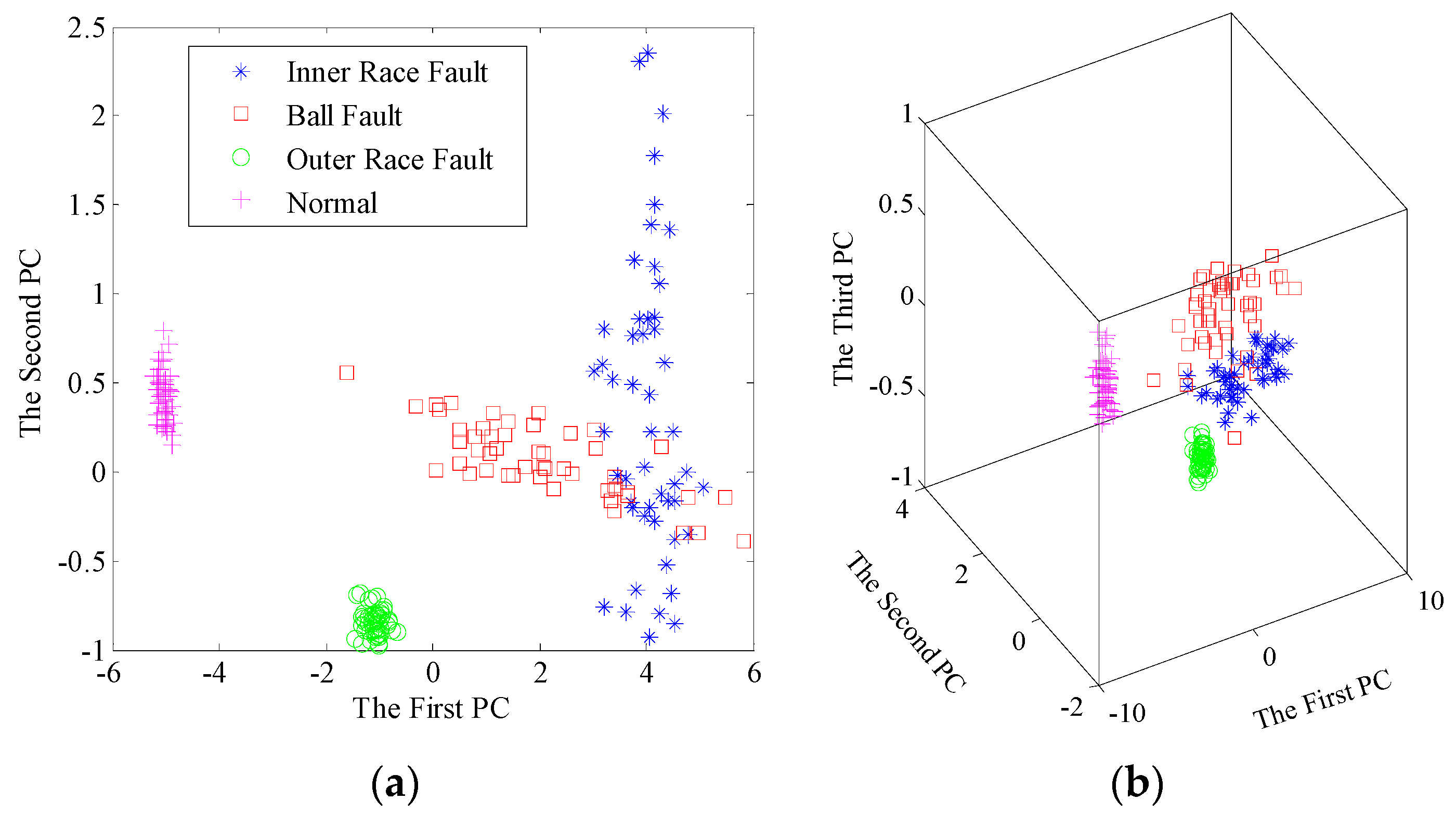
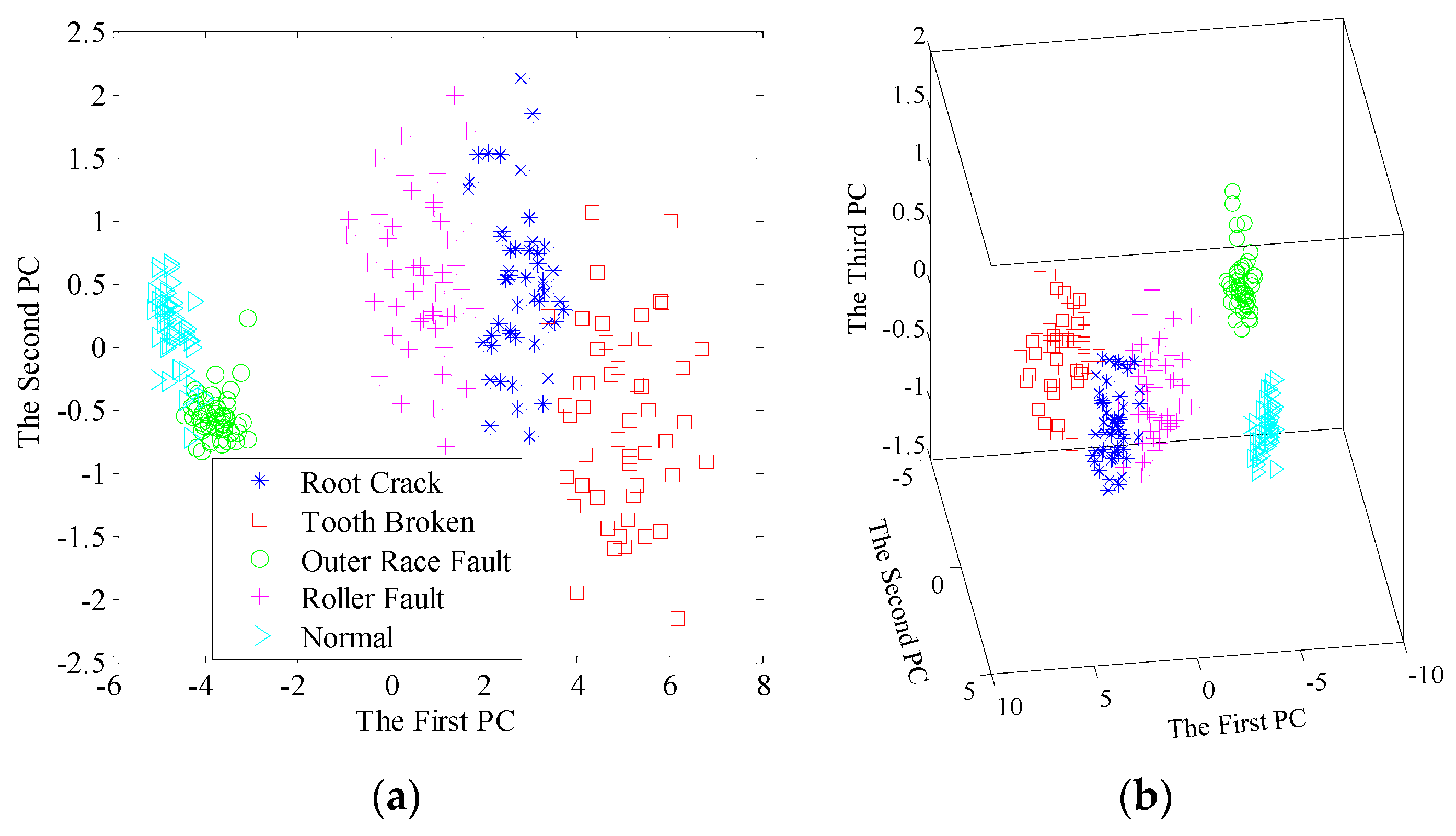
5.2. Case 2: Gearbox Fault Diagnosis Results
5.2.1. Experimental Data
5.2.2. Diagnosis Procedure and Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Guo, L.; Li, N.; Jia, F.; Lei, Y.; Lin, J. A recurrent neural network based health indicator for remaining useful life prediction of bearings. Neurocomputing 2017, 240, 98–109. [Google Scholar] [CrossRef]
- Lei, Y.; Li, N.; Lin, J.; He, Z. Two new features for condition monitoring and fault diagnosis of planetary gearboxes. J. Vib. Control 2013, 21, 755–764. [Google Scholar] [CrossRef]
- Nembhard, A.D.; Sinha, J.K.; Yunusa-Kaltungo, A. Development of a generic rotating machinery fault diagnosis approach insensitive to machine speed and support type. J. Sound Vib. 2015, 337, 321–341. [Google Scholar] [CrossRef]
- Yunusa-Kaltungo, A.; Sinha, J.K. Sensitivity analysis of higher order coherent spectra in machine faults diagnosis. Struct. Health Monit. 2016, 15, 555–567. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A survey of fault diagnosis and fault-tolerant techniques—Part I: Fault diagnosis with model-based and signal-based approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part II: Fault Diagnosis With Knowledge-Based and Hybrid/Active Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3768–3774. [Google Scholar] [CrossRef]
- Liu, W.; Han, J.; Lu, X. A new gear fault feature extraction method based on hybrid time–frequency analysis. Neural Comput. Appl. 2013, 25, 387–392. [Google Scholar] [CrossRef]
- Wang, D.; Shen, C.; Tse, P.W. A novel adaptive wavelet stripping algorithm for extracting the transients caused by bearing localized faults. J. Sound Vib. 2013, 332, 6871–6890. [Google Scholar] [CrossRef]
- An, X.; Jiang, D.; Li, S.; Zhao, M. Application of the ensemble empirical mode decomposition and Hilbert transform to pedestal looseness study of direct-drive wind turbine. Energy 2011, 36, 5508–5520. [Google Scholar] [CrossRef]
- Chen, X.; Feng, F.; Zhang, B. Weak fault feature extraction of rolling bearings based on an improved kurtogram. Sensors 2016, 16, 1482. [Google Scholar] [CrossRef] [PubMed]
- Lei, Y.; He, Z.; Zi, Y. EEMD method and WNN for fault diagnosis of locomotive roller bearings. Expert Syst. Appl. 2011, 38, 7334–7341. [Google Scholar] [CrossRef]
- Lei, Y.; Jia, F.; Lin, J.; Xing, S.; Ding, S.X. An intelligent fault diagnosis method using unsupervised feature learning towards mechanical big data. IEEE Trans. Ind. Electron. 2016, 63, 3137–3147. [Google Scholar] [CrossRef]
- Li, K.; Zhang, Q.; Wang, K.; Chen, P.; Wang, H. Intelligent condition diagnosis method based on adaptive statistic test filter and diagnostic bayesian network. Sensors 2016, 16, 76. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Xu, M.; Wei, Y.; Huang, W. A new rolling bearing fault diagnosis method based on multiscale permutation entropy and improved support vector machine based binary tree. Measurement 2016, 77, 80–94. [Google Scholar] [CrossRef]
- An, X.; Tang, Y. Application of variational mode decomposition energy distribution to bearing fault diagnosis in a wind turbine. Trans. Inst. Meas. Control 2016, 5, 753–772. [Google Scholar] [CrossRef]
- Han, T.; Jiang, D. Rolling bearing fault diagnostic method based on VMD-AR model and random forest classifier. Shock Vib. 2016, 2016, 1–11. [Google Scholar] [CrossRef]
- Elad, M.; Aharon, M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar] [CrossRef] [PubMed]
- Bin, Y.; Shutao, L. Multifocus image fusion and restoration with sparse representation. IEEE Trans. Instrum. Meas. 2010, 59, 884–892. [Google Scholar]
- Yang, S.; Wang, M.; Chen, Y.; Sun, Y. Single-image super-resolution reconstruction via learned geometric dictionaries and clustered sparse coding. IEEE Trans. Image Process. 2012, 21, 4016–4028. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Du, Z.; Li, J.; Li, X.; Zhang, H. Compressed sensing based on dictionary learning for extracting impulse components. Signal Process. 2014, 96, 94–109. [Google Scholar] [CrossRef]
- Tang, H.; Chen, J.; Dong, G. Sparse representation based latent components analysis for machinery weak fault detection. Mech. Syst. Signal Process. 2014, 46, 373–388. [Google Scholar] [CrossRef]
- Liu, H.; Liu, C.; Huang, Y. Adaptive feature extraction using sparse coding for machinery fault diagnosis. Mech. Syst. Signal Process. 2011, 25, 558–574. [Google Scholar] [CrossRef]
- Zhou, H.; Chen, J.; Dong, G.; Wang, R. Detection and diagnosis of bearing faults using shift-invariant dictionary learning and hidden Markov model. Mech. Syst. Signal Process. 2016, 72, 65–79. [Google Scholar] [CrossRef]
- Guo, L.; Gao, H.; Li, J.; Huang, H.; Zhang, X. Machinery vibration signal denoising based on learned dictionary and sparse representation. J. Phys. Conf. Ser. 2015, 628, 012124. [Google Scholar] [CrossRef]
- Donoho, D.L.; Elad, M.; Temlyakov, V.N. Stable recovery of sparse overcomplete representations in the presence of noise. IEEE Trans. Inf. Theory 2006, 52, 6–18. [Google Scholar] [CrossRef]
- Bruckstein, A.M.; Donoho, D.L.; Elad, M. From sparse solutions of systems of equations to sparse modeling of signals and images. SIAM Rev. 2009, 51, 34–81. [Google Scholar] [CrossRef]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Sulam, J.; Ophir, B.; Zibulevsky, M.; Elad, M. Trainlets: Dictionary learning in high dimensions. IEEE Trans. Signal Process. 2016, 64, 3180–3193. [Google Scholar] [CrossRef]
- Kilundu, B.; Chiementin, X.; Dehombreux, P. Singular spectrum analysis for bearing defect detection. J. Vib. Acoust. 2011, 133, 051007. [Google Scholar] [CrossRef]
- Muruganatham, B.; Sanjith, M.A.; Krishnakumar, B.; Satya Murty, S.A.V. Roller element bearing fault diagnosis using singular spectrum analysis. Mech. Syst. Signal Process. 2013, 35, 150–166. [Google Scholar] [CrossRef]
- Han, T.; Jiang, D.; Wang, N. The fault feature extraction of rolling bearing based on EMD and difference spectrum of singular value. Shock Vib. 2016, 2016, 1–14. [Google Scholar] [CrossRef]
- Cheng, J.; Yu, D.; Tang, J. Application of SVM and SVD technique based on EMD to the fault diagnosis of the rotating machinery. Shock Vib. 2009, 16, 89–98. [Google Scholar] [CrossRef]
- Luo, S.; Cheng, J.; Ao, H. Application of LCD-SVD technique and CRO-SVM method to fault diagnosis for roller bearing. Shock Vib. 2015, 2015, 1–8. [Google Scholar] [CrossRef]
- Tian, Y.; Ma, J.; Lu, C.; Wang, Z. Rolling bearing fault diagnosis under variable conditions using LMD-SVD and extreme learning machine. Mech. Mach. Theory 2015, 90, 175–186. [Google Scholar] [CrossRef]
- Huang, N.; Chen, H.; Cai, G.; Fang, L.; Wang, Y. Mechanical fault diagnosis of high voltage circuit breakers based on variational mode decomposition and multi-layer classifier. Sensors 2016, 16, 1887. [Google Scholar] [CrossRef] [PubMed]
- Yunusa-Kaltungo, A.; Sinha, J.K.; Nembhard, A.D. A novel fault diagnosis technique for enhancing maintenance and reliability of rotating machines. Struct. Health Monit. 2015, 14, 604–621. [Google Scholar] [CrossRef]
- Wang, D.; Tsui, K.-L.; Tse, P.W.; Zuo, M.J. Principal components of superhigh-dimensional statistical features and support vector machine for improving identification accuracies of different gear crack levels under different working conditions. Shock Vib. 2015, 2015, 1–14. [Google Scholar] [CrossRef]
- Van Der Maaten, L.; Postma, E.; van den Herik, J. Dimensionality reduction: A comparative review. J. Mach. Learn. Res. 2009, 10, 66–71. [Google Scholar]


| Initial Dictionary | Overlap Size | Sparse Coding | Noise Level | Update Iterations |
|---|---|---|---|---|
| DCT | Maximum overlap ratio | OMP | Wavelet coefficient estimator | 20 |
| Pre-Processor | First PC | First Two PCs | First Three PCs |
|---|---|---|---|
| Dictionary learning | 0.881 | 0.955 | 0.976 |
| EMD | 0.952 | 0.988 | 0.994 |
| Pre-Processor | First PC | First Two PCs | First Three PCs |
|---|---|---|---|
| Dictionary learning | 0.747 | 0.843 | 0.907 |
| EMD | 0.935 | 0.973 | 0.989 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, T.; Jiang, D.; Zhang, X.; Sun, Y. Intelligent Diagnosis Method for Rotating Machinery Using Dictionary Learning and Singular Value Decomposition. Sensors 2017, 17, 689. https://doi.org/10.3390/s17040689
Han T, Jiang D, Zhang X, Sun Y. Intelligent Diagnosis Method for Rotating Machinery Using Dictionary Learning and Singular Value Decomposition. Sensors. 2017; 17(4):689. https://doi.org/10.3390/s17040689
Chicago/Turabian StyleHan, Te, Dongxiang Jiang, Xiaochen Zhang, and Yankui Sun. 2017. "Intelligent Diagnosis Method for Rotating Machinery Using Dictionary Learning and Singular Value Decomposition" Sensors 17, no. 4: 689. https://doi.org/10.3390/s17040689







