Spectroscopic Diagnosis of Arsenic Contamination in Agricultural Soils
Abstract
:1. Introduction
2. Materials and Methods
2.1. Soil Samples
2.2. Laboratory Spectrum and Soil Arsenic Content Measurement
2.3. Pre-Processing Transformations
2.4. Feature Selection
2.5. Multivariate Diagnosis Analysis
2.5.1. Random Forests (RF)
2.5.2. Artificial Neural Network (ANN)
2.5.3. Support Vector Machine (SVM)
2.6. Validation and Comparison of Diagnosis Models
3. Results
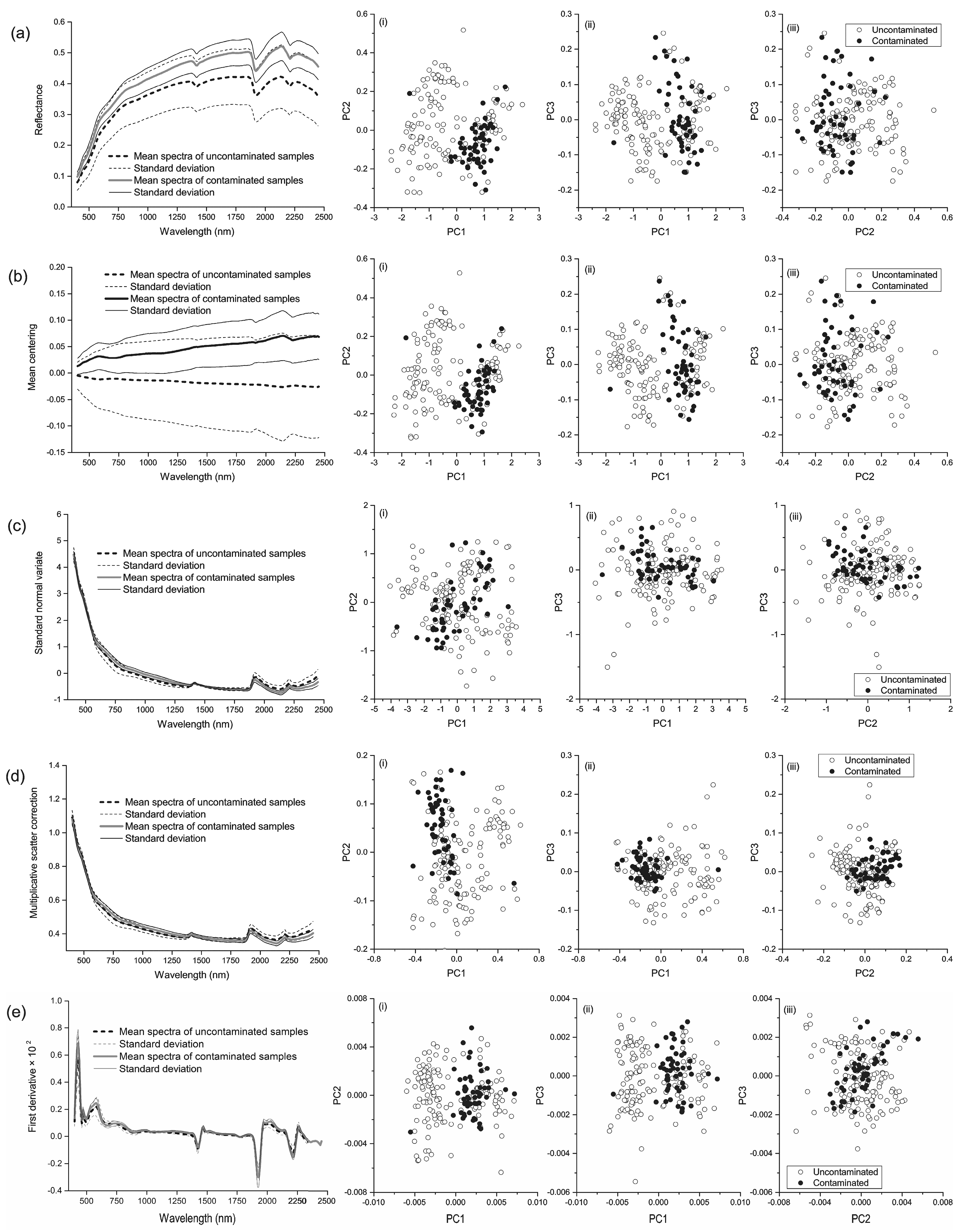
3.1. Soil Arsenic and the Spectra
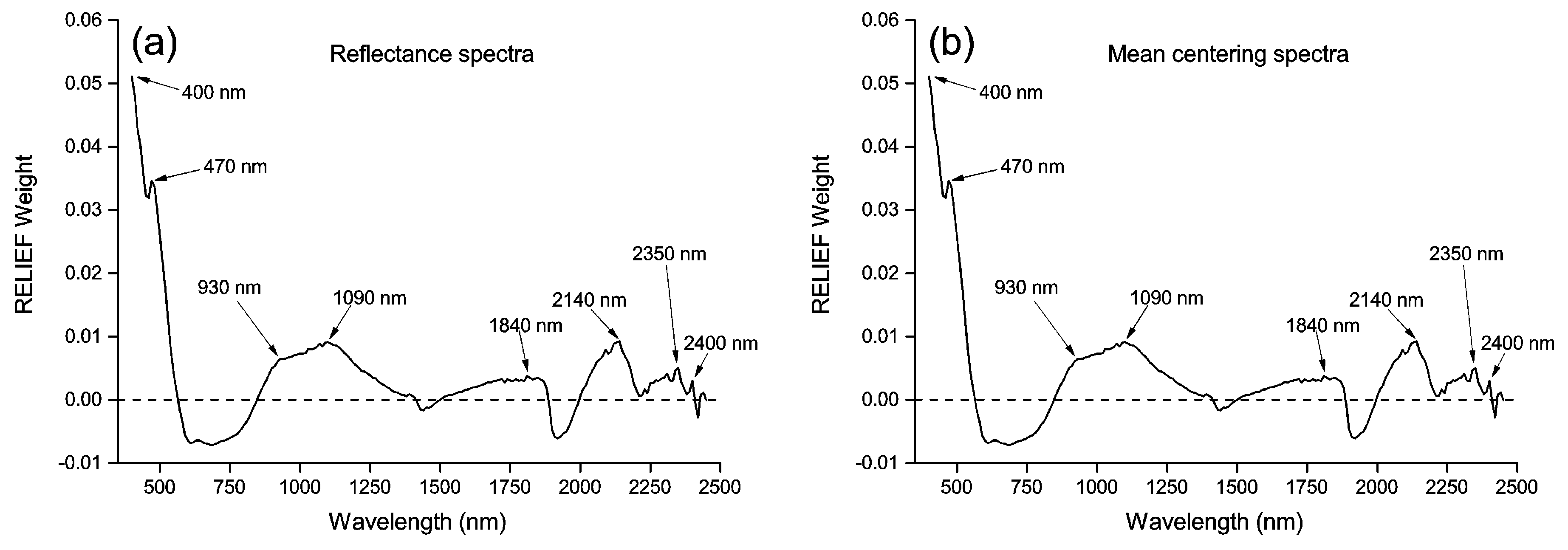
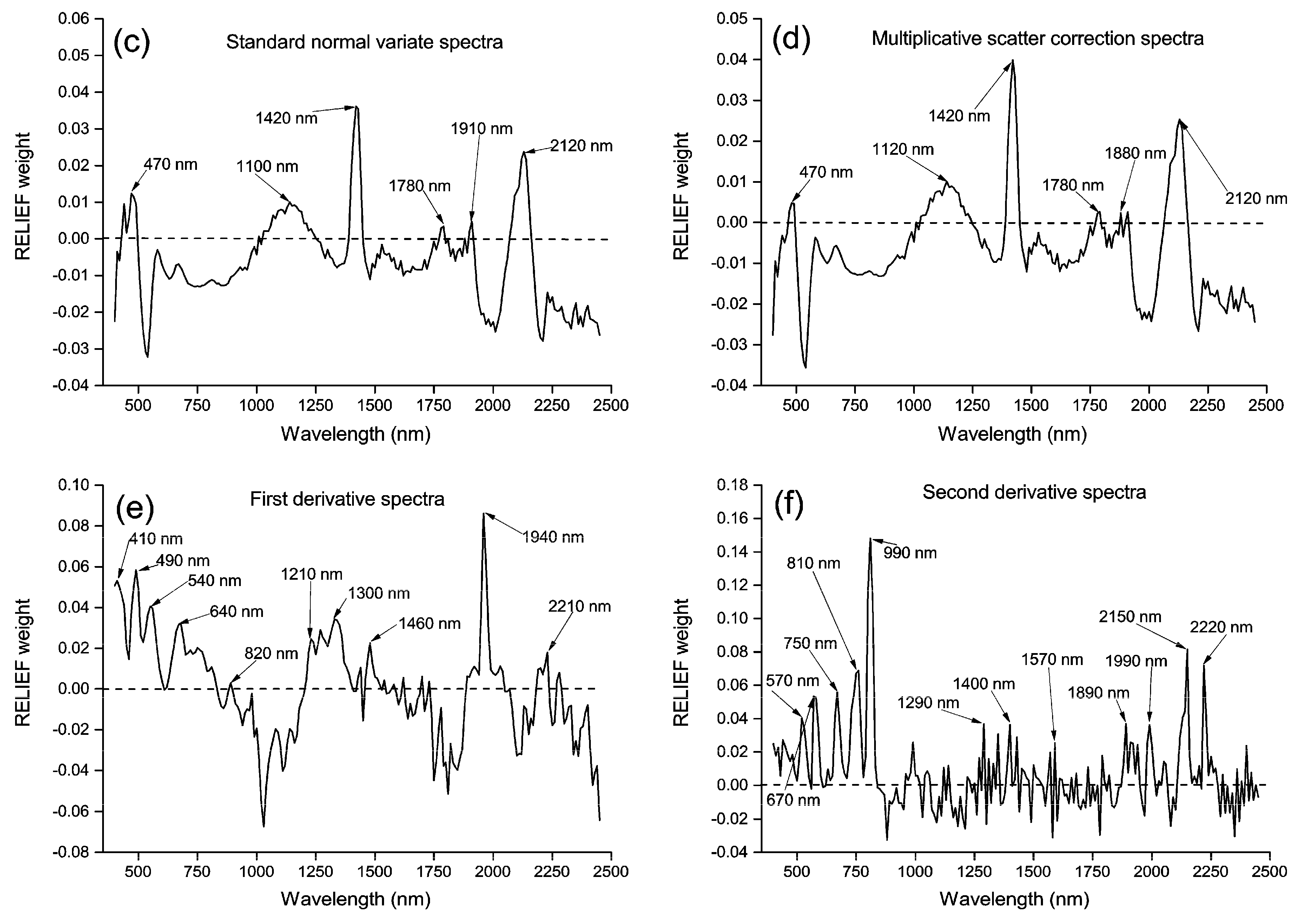
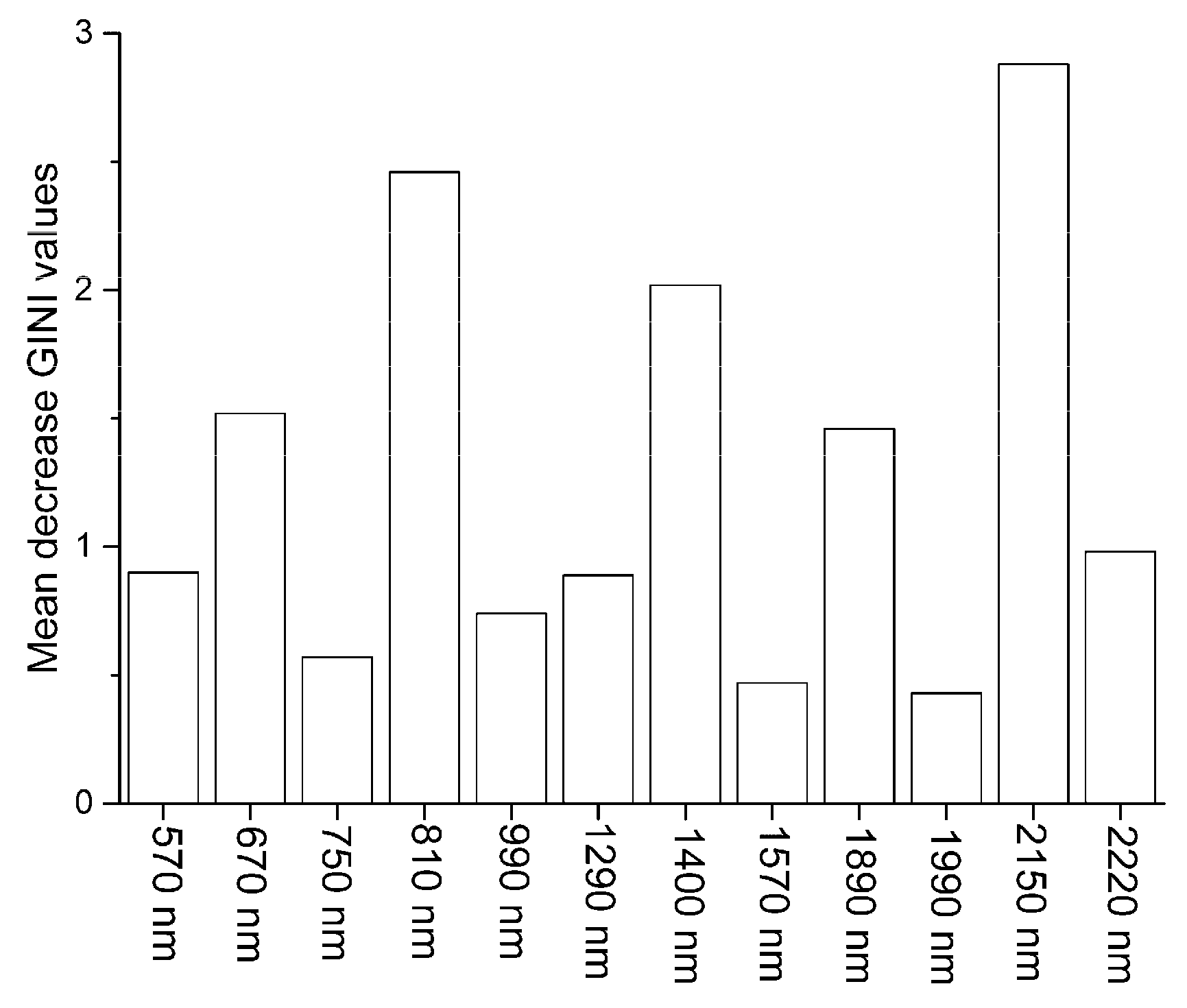
3.2. Principal Components and RELIEF Selected Features
3.3. Comparison of the Abilities of Different Methods
3.3.1. RF
3.3.2. ANN
3.3.3. SVM
3.3.4. Model Comparison
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shi, T.Z.; Chen, Y.Y.; Liu, Y.L.; Wu, G.F. Visible and near-infrared reflectance spectroscopy—An alternative for monitoring soil contamination by heavy metal. J. Hazard. Mater. 2014, 265, 166–176. [Google Scholar] [CrossRef] [PubMed]
- Viscarra Rossel, R.A.; Walvoort, D.J.J.; McBratney, A.B.; Janik, L.J.; Skjemstad, J.O. Visible, near infrared, mid infrared or combined diffuse reflectance spectroscopy for simultaneous assessment of various soil properties. Geoderma 2006, 131, 59–75. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Irons, J.R.; Epema, G.F. Remote Sensing of the Earth Sciences: Manual of Remote Sensing; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Kemper, T.; Sommer, S. Estimate of heavy metal contamination in soils after a mining accident using reflectance spectroscopy. Environ. Sci. Technol. 2002, 36, 2742–2747. [Google Scholar] [CrossRef] [PubMed]
- Chu, X.L.; Yuan, H.F.; Lu, W.Z. Progress and application of spectral data pretreatment and wavelength selection methods in nir analytical technique. Prog. Chem. 2004, 16, 528–542. (In Chinese) [Google Scholar]
- Stenberg, B.; Viscarra Rossel, R.A.; Mouazen, A.M.; Wetterlind, J. Visible and Near Infrared Spectroscopy in Soil Science; Agronomy, A.I., Ed.; Academic Press: Burlington, VT, USA, 2010; Volume 107, pp. 163–215. [Google Scholar]
- Vohland, M.; Emmerling, C. Determination of total soil organic c and hot water-extractable c from vis-nir soil reflectance with partial least squares regression and spectral feature selection techniques. Eur. J. Soil Sci. 2011, 62, 598–606. [Google Scholar] [CrossRef]
- Shi, T.Z.; Chen, Y.Y.; Liu, H.Z.; Wang, J.J.; Wu, G.F. Soil organic carbon content estimation with laboratory-based visible-near-infrared reflectance spectroscopy: Feature selection. Appl. Spectrosc. 2014, 68, 831–837. [Google Scholar] [CrossRef] [PubMed]
- Araújo, M.C.U.; Saldanha, T.C.B.; Galvão, R.K.H.; Yoneyama, T.; Chame, H.C.; Visani, V. The successive projections algorithm for variable selection in spectroscopic multicomponent analysis. Chemom. Intell. Lab. Syst. 2001, 57, 65–73. [Google Scholar] [CrossRef]
- Zou, X.B.; Zhao, J.W.; Malcolm, J.W.; Holmes, M.; Mao, H.P. Variables selection methods in near-infrared spectroscopy. Anal. Chim. Acta 2010, 667, 14–32. [Google Scholar]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Witten, I.H.; Frank, E. Data Mining: Practical Machine Learning Tools and Techniques; Elsevier: San Francisco, CA, USA, 2005. [Google Scholar]
- Wu, Y.Z.; Chen, J.; Ji, J.F.; Tian, Q.J.; Wu, X.M. Feasibility of reflectance spectroscopy for the assessment of soil mercury contamination. Environ. Sci. Technol. 2005, 39, 873–878. [Google Scholar] [CrossRef] [PubMed]
- Kooistra, L.; Wehrens, R.; Leuven, R.S.E.W.; Buydens, L.M.C. Possibilities of visible-near-infrared spectroscopy for the assessment of soil contamination in river floodplains. Anal. Chim. Acta 2001, 446, 97–105. [Google Scholar] [CrossRef]
- Wu, Y.Z.; Chen, J.; Wu, X.M.; Tian, Q.J.; Ji, J.F.; Qin, Z.H. Possibilities of reflectance spectroscopy for the assessment of contaminant elements in suburban soils. Appl. Geochem. 2005, 20, 1051–1059. [Google Scholar] [CrossRef]
- Chen, T.; Chang, Q.R.; Clevers, J.G.P.W.; Kooistra, L. Rapid identification of soil cadmium pollution risk at regional scale based on visible and near-infrared spectroscopy. Environ. Pollut. 2015, 206, 217–226. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.Z.; Zhang, X.; Liao, Q.L.; Ji, J.F. Can contaminant elements in soils be assessed by remote sensing technology: A case study with simulated data. Soil Sci. 2011, 176, 196–205. [Google Scholar] [CrossRef]
- Tan, K.; Ye, Y.Y.; Du, P.J.; Zhang, Q.Q. Estimation of heavy metal concentrations in reclaimed mining soils using reflectance spectroscopy. Spectrosc. Spectr. Anal. 2014, 34, 3317–3322. [Google Scholar]
- Lucà, F.; Conforti, M.; Castrignanò, A.M.; Matteucci, G.; Buttafuoco, G. Effect of calibration set size on prediction at local scale of soil carbon by vis-nir spectroscopy. Geoderma 2017, 288, 175–183. [Google Scholar] [CrossRef]
- Shi, T.Z.; Cui, L.J.; Wang, J.J.; Fei, T.; Chen, Y.Y.; Wu, G.F. Comparison of multivariate methods for estimating soil total nitrogen with visible/near-infrared spectroscopy. Plant Soil 2013, 366, 363–375. [Google Scholar] [CrossRef]
- Heung, B.; Ho, H.C.; Zhang, J.; Knudby, A.; Bulmer, C.E.; Schmidt, M.G. An overview and comparison of machine-learning techniques for classification purposes in digital soil mapping. Geoderma 2016, 265, 62–77. [Google Scholar] [CrossRef]
- Brungard, C.W.; Boettinger, J.L.; Duniway, M.C.; Wills, S.A.; Edwards, T.C. Machine learning for predicting soil classes in three semi-arid landscapes. Geoderma 2015, 239–240, 68–83. [Google Scholar] [CrossRef]
- Bray, J.G.P.; Viscarra Rossel, R.A.; McBratney, A.B. Diagnostic screening of urban soil contaminations using diffuse reflectance spectroscopy. Aust. J. Soil Sci. 2009, 47, 433–442. [Google Scholar] [CrossRef]
- Ren, H.Y.; Zhuang, D.F.; Singh, A.N.; Pan, J.J.; Qiu, D.S.; Shi, R.H. Estimation of as and cu contamination in agricultural soils around a mining area by reflectance spectroscopy: A case study. Pedosphere 2009, 19, 719–726. [Google Scholar] [CrossRef]
- Vohland, M.; Besold, J.; Hill, J.; Frund, H.C. Comparing different multivariate calibration methods for the determination of soil organic carbon pools with visible to near infrared spectroscopy. Geoderma 2011, 166, 198–205. [Google Scholar] [CrossRef]
- Huang, R.Q.; Gao, S.F.; Wang, W.L.; Staunton, S.; Wang, G. Soil arsenic availability and the transfer of soil arsenic to crops in suburban areas in fujian province, southeast China. Sci. Total Environ. 2006, 368, 531–541. [Google Scholar] [CrossRef] [PubMed]
- Santra, S.C.; Samal, A.C.; Bhattacharya, P.; Banerjee, S.; Biswas, A.; Majumdar, J. Arsenic in foodchain and community health risk: A study in gangetic west bengal. Procedia Environ. Sci. 2013, 18, 2–13. [Google Scholar] [CrossRef]
- Shi, T.Z.; Liu, H.Z.; Wang, J.J.; Chen, Y.Y.; Fei, T.; Wu, G.F. Monitoring arsenic contamination in agricultural soils with reflectance spectroscopy of rice plants. Environ. Sci. Technol. 2014, 48, 6264–6272. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.J.; Cui, L.J.; Gao, W.X.; Shi, T.Z.; Chen, Y.Y.; Gao, Y. Prediction of low heavy metal concentrations in agricultural soils using visible and near-infrared reflectance spectroscopy. Geoderma 2014, 216, 1–9. [Google Scholar] [CrossRef]
- Guo, J.H.; Ma, H.; Wang, S.F. Determination of arsenic in national standard reference soil and stream sediment samples by atomic fluorescence spectrometry. Rock Miner. Anal. 2009, 28, 182–184. (In Chinese) [Google Scholar]
- Loska, K.; Wiechula, D.; Korus, I. Metal contamination of farming soils affected by industry. Environ. Int. 2004, 30, 159–165. [Google Scholar] [CrossRef]
- Kennard, R.W.; Stone, L.A. Computer aided design of experiments. Technometrics 1969, 11, 137–148. [Google Scholar] [CrossRef]
- Kira, K.; Rendell, L. A practical appoach to feature selection. In The Ninth International Workshop on Machine Learning; Sleeman, D., Edwards, P., Eds.; Morgan Kaufmann: Aberdeen, UK, 1992. [Google Scholar]
- Williams, G.J. Rattle: A data mining gui for R. R J. 2009, 1, 45–55. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 54, 115–133. [Google Scholar] [CrossRef]
- Behrens, T.; Förster, H.; Scholten, T.; Steinrücken, U.; Spies, E.D.; Goldschmitt, M. Digital soil mapping using artificial neural networks. J. Plant Nutri. Soil Sci. 2005, 168, 21–33. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Kampichler, C.; Wieland, R.; Calme, S.; Weissenberger, H.; Arriaga-Weiss, S. Classification in conservation biology: A comparison of five machine-learning methods. Ecol. Inf. 2010, 5, 441–450. [Google Scholar] [CrossRef]
- Foody, G.M. Thematic map comparison: Evaluating the statistical significance of differences in classification accuracy. Photogramm. Eng. Remote Sensing 2004, 70, 623–633. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.; Behrens, T. Using data mining to model and interpret soil diffuse reflectance spectra. Geoderma 2010, 158, 46–54. [Google Scholar] [CrossRef]
- Van Groenigen, J.W.; Mutters, C.S.; Horwath, W.R.; van Kessel, C. Nir and drift-mir spectrometry of soils for predicting soil and crop parameters in a flooded field. Plant Soil 2003, 250, 155–165. [Google Scholar] [CrossRef]
- Vinterbo, S.A.; Kim, E.Y.; Ohno-Machado, L. Small, fuzzy and interpretable gene expression based classifiers. Bioinformatics 2005, 21, 1964–1970. [Google Scholar] [CrossRef] [PubMed]
- Choe, E.; van der Meer, F.; van Ruitenbeek, F.; van der Werff, H.; de Smeth, B.; Kim, K.W. Mapping of heavy metal pollution in stream sediments using combined geochemistry, field spectroscopy, and hyperspectral remote sensing: A case study of the rodalquilar mining area, se spain. Remote Sensing Environ. 2008, 112, 3222–3233. [Google Scholar] [CrossRef]
- Kemper, T.; Sommer, S. Use fo airborne hyperspectral data to estimate residual heavy metal contamination and acidification potential in the guadiamar floodplain andalusia, spain after the aznacollar mining accident. Proc. SPIE 2004, 5574, 224–234. [Google Scholar]
- Stevens, A.; Udelhoven, T.; Denis, A.; Tychon, B. Measuring soil organic carbon in croplands at regional scale using airborne imaging spectroscopy. Geoderma 2010, 158, 32–45. [Google Scholar] [CrossRef]



| Allocation | Observed | ||
|---|---|---|---|
| Contaminated (Positive, Value = 1) | Uncontaminated (Negative, Value = 0) | ||
| Predicted | Contaminated (positive, value = 1) | pp | np |
| Uncontaminated (negative, value = 0) | pn | nn | |
| Allocation | Diagnosis Model 2 | ||
|---|---|---|---|
| Correct | Incorrect | ||
| Diagnosis model 1 | Correct | f11 | f12 |
| Incorrect | f21 | f22 | |
| No. | Minimum | Maximum | Mean | Std. | Per % | |
|---|---|---|---|---|---|---|
| Total data set | 195 | 1.91 | 133.36 | 18.13 | 18.67 | 27 |
| Training data set | 98 | 1.91 | 106.10 | 12.70 | 16.81 | 26 |
| Test data set | 97 | 4.40 | 133.36 | 19.00 | 20.43 | 29 |
| Machine-Learning Methods | Pre-Processing Methods | Feature Selection Methods | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No Feature Selection | PCA | RELIEF | ||||||||||||||||||||||
| Parameters | time (s) | OA (%) | nPC | Parameters | time (s) | OA (%) | nfeature | Parameters | time (s) | OA (%) | ||||||||||||||
| nt | nv | nt | nv | nt | nv | |||||||||||||||||||
| RF | none | 70 | 5 | 0.32 | 80 | 5 | 60 | 7 | 0.22 | 82 | 8 | 150 | 5 | 0.04 | 85 | |||||||||
| MC | 270 | 4 | 0.27 | 74 | 7 | 160 | 2 | 0.17 | 83 | 8 | 130 | 3 | 0.03 | 71 | ||||||||||
| SNV | 290 | 3 | 0.32 | 84 | 7 | 20 | 2 | 0.05 | 70 | 6 | 60 | 3 | 0.03 | 82 | ||||||||||
| MSC | 150 | 4 | 0.25 | 71 | 6 | 30 | 2 | 0.03 | 71 | 6 | 30 | 2 | 0.03 | 71 | ||||||||||
| 1st | 50 | 2 | 0.25 | 77 | 8 | 80 | 4 | 0.05 | 79 | 10 | 30 | 3 | 0.03 | 81 | ||||||||||
| 2nd | 200 | 2 | 0.28 | 85 | 6 | 50 | 4 | 0.05 | 71 | 12 | 50 | 2 | 0.05 | 86 | ||||||||||
| Parameters | time (s) | OA (%) | nPC | Parameters | time (s) | OA (%) | nfeature | Parameters | time (s) | OA (%) | ||||||||||||||
| nlayer | nlayer | nlayer | ||||||||||||||||||||||
| ANN | none | 1 | 0.34 | 86 | 6 | 9 | 0.05 | 71 | 8 | 3 | 0.02 | 84 | ||||||||||||
| MC | 2 | 0.48 | 76 | 8 | 2 | 0.04 | 71 | 8 | 10 | 0.05 | 76 | |||||||||||||
| SNV | 1 | 0.27 | 81 | 6 | 2 | 0.03 | 64 | 6 | 6 | 0.03 | 86 | |||||||||||||
| MSC | 1 | 0.28 | 29 | 8 | 2 | 0.03 | 40 | 6 | 3 | 0.02 | 52 | |||||||||||||
| 1st | 3 | 0.67 | 87 | 8 | 3 | 0.03 | 89 | 10 | 1 | 0.03 | 81 | |||||||||||||
| 2nd | 1 | 0.30 | 82 | 5 | 2 | 0.03 | 62 | 12 | 1 | 0.03 | 75 | |||||||||||||
| Parameters | time (s) | OA (%) | nPC | Parameters | time (s) | OA (%) | nfeature | Parameters | time (s) | OA (%) | ||||||||||||||
| γ | C | nsv | γ | C | nsv | γ | C | nsv | ||||||||||||||||
| RBF-SVM | none | 0.01 | 1 | 32 | 0.11 | 80 | 7 | 0.04 | 1 | 32 | 0.05 | 85 | 8 | 0.17 | 1 | 32 | 0.02 | 82 | ||||||
| MC | 0.01 | 1 | 32 | 0.14 | 70 | 7 | 0.08 | 1 | 35 | 0.05 | 87 | 8 | 0.38 | 1 | 31 | 0.03 | 76 | |||||||
| Machine-learning methods | Pre-processing methods | Feature selection methods | ||||||||||||||||||||||
| No feature selection | PCA | RELIEF | ||||||||||||||||||||||
| Parameters | time (s) | OA (%) | nPC | Parameters | time (s) | OA (%) | nfeature | Parameters | time (s) | OA (%) | ||||||||||||||
| γ | C | nsv | γ | C | nsv | γ | C | nsv | ||||||||||||||||
| RBF-SVM | SNV | 0.01 | 1 | 36 | 0.09 | 81 | 9 | 0.04 | 1 | 42 | 0.04 | 66 | 6 | 0.28 | 1 | 36 | 0.03 | 80 | ||||||
| MSC | 0.01 | 1 | 37 | 0.08 | 71 | 5 | 0.23 | 1 | 38 | 0.03 | 71 | 6 | 0.31 | 1 | 37 | 0.02 | 71 | |||||||
| 1st | 0.01 | 1 | 46 | 0.06 | 79 | 8 | 0.05 | 1 | 43 | 0.05 | 75 | 10 | 0.09 | 1 | 33 | 0.33 | 82 | |||||||
| 2nd | 0.01 | 1 | 53 | 0.08 | 81 | 5 | 0.07 | 1 | 41 | 0.03 | 71 | 12 | 0.06 | 1 | 42 | 0.05 | 89 | |||||||
| Parameters | time (s) | OA (%) | nPC | Parameters | time (s) | OA (%) | nfeature | Parameters | time (s) | OA (%) | ||||||||||||||
| C | nsv | C | nsv | C | nsv | |||||||||||||||||||
| LF-SVM | none | 1 | 36 | 0.16 | 84 | 7 | 1 | 35 | 0.05 | 81 | 8 | 1 | 37 | 0.05 | 80 | |||||||||
| MC | 1 | 36 | 0.12 | 85 | 7 | 1 | 35 | 0.05 | 85 | 8 | 1 | 35 | 0.03 | 79 | ||||||||||
| SNV | 1 | 33 | 0.11 | 86 | 5 | 1 | 27 | 0.06 | 56 | 6 | 1 | 39 | 0.06 | 72 | ||||||||||
| MSC | 1 | 34 | 0.11 | 29 | 5 | 1 | 39 | 0.06 | 29 | 6 | 1 | 39 | 0.04 | 73 | ||||||||||
| 1st | 1 | 26 | 0.09 | 80 | 8 | 1 | 27 | 0.05 | 80 | 10 | 1 | 29 | 0.05 | 87 | ||||||||||
| 2nd | 1 | 36 | 0.10 | 76 | 4 | 1 | 30 | 0.06 | 63 | 12 | 1 | 26 | 0.05 | 81 | ||||||||||
| Second + RELIEF + RF | First + PCA + ANN | Second + RELIEF + RBF-SVM | |
|---|---|---|---|
| First + PCA + ANN | 0.24 | ||
| Second + RELIEF + RBF-SVM | 0.90 | 0.00 | |
| First + RELIEF + LF-SVM | 0.30 | 0.26 | 0.41 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, T.; Liu, H.; Chen, Y.; Fei, T.; Wang, J.; Wu, G. Spectroscopic Diagnosis of Arsenic Contamination in Agricultural Soils. Sensors 2017, 17, 1036. https://doi.org/10.3390/s17051036
Shi T, Liu H, Chen Y, Fei T, Wang J, Wu G. Spectroscopic Diagnosis of Arsenic Contamination in Agricultural Soils. Sensors. 2017; 17(5):1036. https://doi.org/10.3390/s17051036
Chicago/Turabian StyleShi, Tiezhu, Huizeng Liu, Yiyun Chen, Teng Fei, Junjie Wang, and Guofeng Wu. 2017. "Spectroscopic Diagnosis of Arsenic Contamination in Agricultural Soils" Sensors 17, no. 5: 1036. https://doi.org/10.3390/s17051036
APA StyleShi, T., Liu, H., Chen, Y., Fei, T., Wang, J., & Wu, G. (2017). Spectroscopic Diagnosis of Arsenic Contamination in Agricultural Soils. Sensors, 17(5), 1036. https://doi.org/10.3390/s17051036







