1. Introduction
Two-wheeled inverted pendulum (TWIP) vehicles are a popular test platform to validate the performance of advanced control algorithms, such as the control capacity for nonlinear, instability and rapidity situations. The motion of a TWIP vehicle is governed by its under-actuated configuration, which makes it difficult to control by simply applying traditional robotics approaches [
1]. In recent years, control design for the stability and robustness of TWIP vehicles has attracted great research interest. In [
2], a neural network control method was proposed for an under-actuated wheeled inverted pendulum model with small overshoot and quick response to changes in the desired trajectories. In [
3], adaptive backstepping control for a two-wheeled autonomous robot around an operating point was investigated. In [
4], an adaptation concept was brought into neural network control, which demonstrated the yaw angle and pitch angle convergence time was less than 0.4 s with an initial value of 0.3 rad.
The sliding mode control (SMC) method was first proposed by Soviet scholars in the 1960s. The SMC method has some advantages such as robustness to parameter uncertainty, insensitivity to bounded disturbances, fast dynamic response, a remarkable computational simplicity with respect to other robust control approaches, and easy implementation of the controller [
5,
6]. However, the chattering caused by the discontinuous sliding controller more or less limits its application in practice [
7].
The high-order sliding mode control (HOSMC) method is the further improvement of the traditional sliding mode control, yielding less chattering and better convergence accuracy while preserving its robustness properties [
8,
9]. Consequently, HOSMC methods have been actively investigated in recent years for chattering attenuation and robust control of unknown uncertainties and perturbations, respectively. Levant put forward the 2-SMC method based on a differentiation and output-feedback control system in [
10], and there are many different 2-SMC algorithms that have been presented such as the ‘twisting’ and ‘super-twisting’ ones put forward by Levant, the ‘sub-optimal’ and ‘global’ ones developed by Bartolini and so on.
The objective of this paper is to sustain the self-balance and trajectory tracking of a TWIP vehicle in a GPS denied environment. Nakano et al. have proposed an estimation/control structure in a two-wheeled vehicle where both a camera and a target object are attached to the vehicle [
11]. The major drawback of the approach based on camera is that it may produce a heavy computational load and lead to a low real-time performance. Accuracy and precision are the two main performance parameters of the indoor localization system. Portable UWB radio ranging technology was introduced in [
12,
13]. The UWB local positioning system can be used as a standalone system or as a complementary system where the GPS is unavailable or denied, can meet high real-time requirements and even penetrate through objects (such as walls, obstacles, bodies, etc.) to a certain extent.
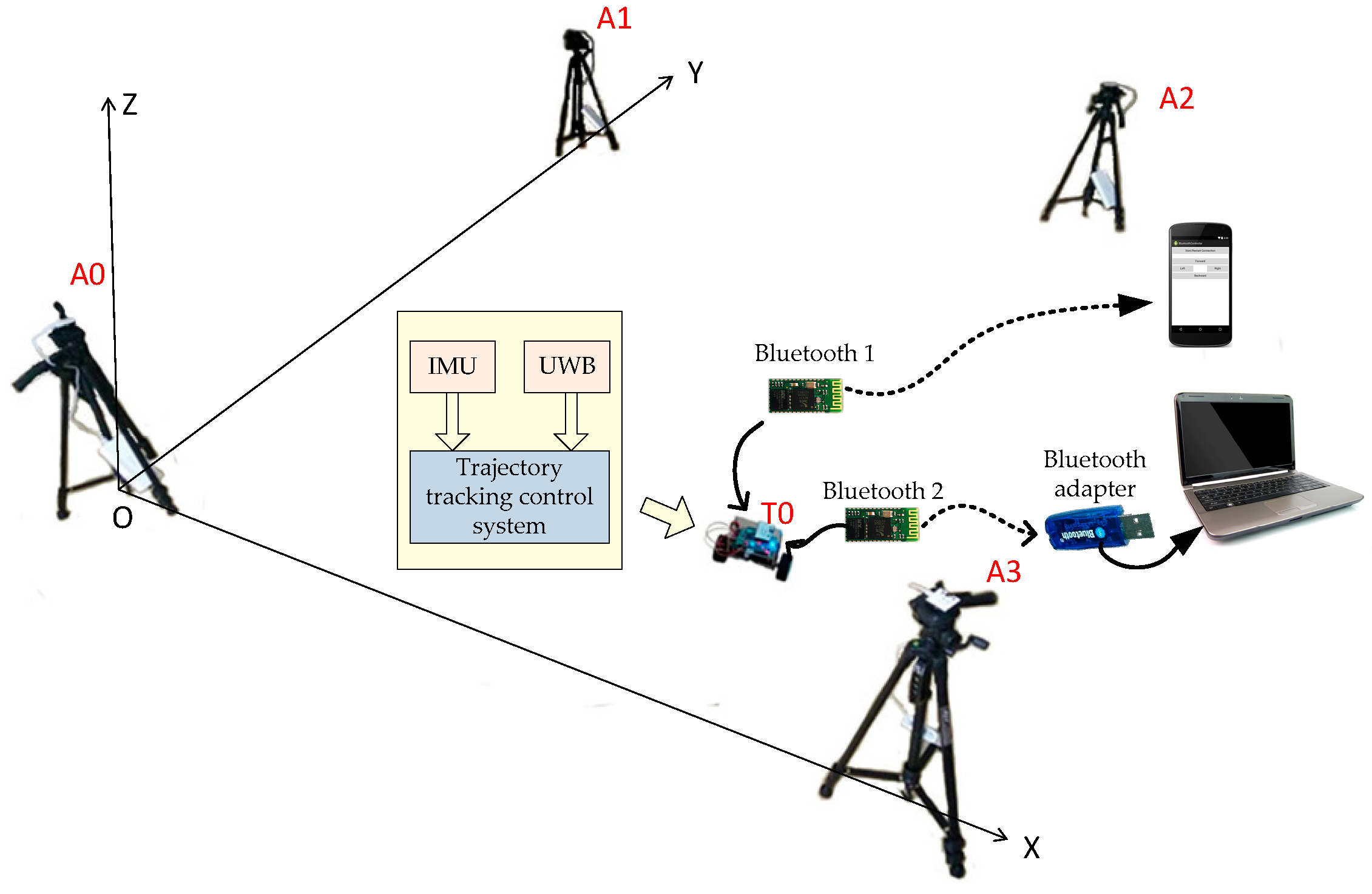
In this paper, a prototype TWIP vehicle (shown in
Figure 1) was built in our lab. The TWIP vehicle consists of two independent drive wheels on the same axle, two rotary encoders, a car body and other auxiliary devices such as a sensor (MPU-6050) which has an embedded 3-axis MEMS gyroscope, a 3-axis MEMS accelerometer (MEMS sensors have the advantages of miniaturization and high-performance [
14]) and a portable I-UWB locating tag.
The control system configuration of our testbed is illustrated in
Figure 2. The attitude data of the TWIP vehicle is measured via the onboard IMU, the location information of the TWIP vehicle is measured by an onboard UWB receiver and used to control the motion of the vehicle. In
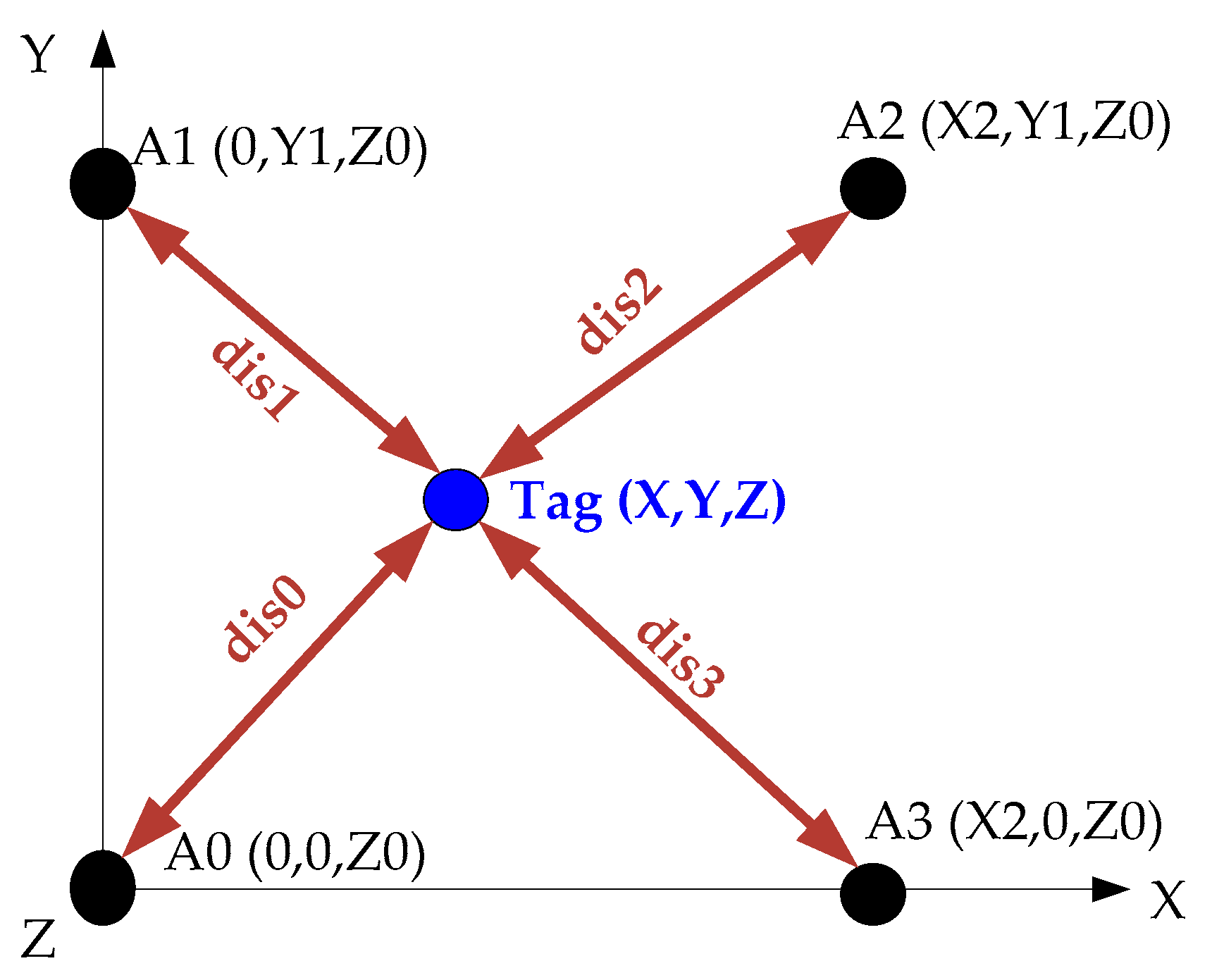
Figure 2, A0, A1, A2 and A3 are four UWB positioning technology anchors, T0 is a UWB receiver used as an onboard tag. The TWIP vehicle can communicate with both cellphones and laptops via Bluetooth devices.
This paper is organized as follows: in
Section 2, the nonlinear dynamic model of the TWIP vehicle is established using a Lagrange energy equation. In
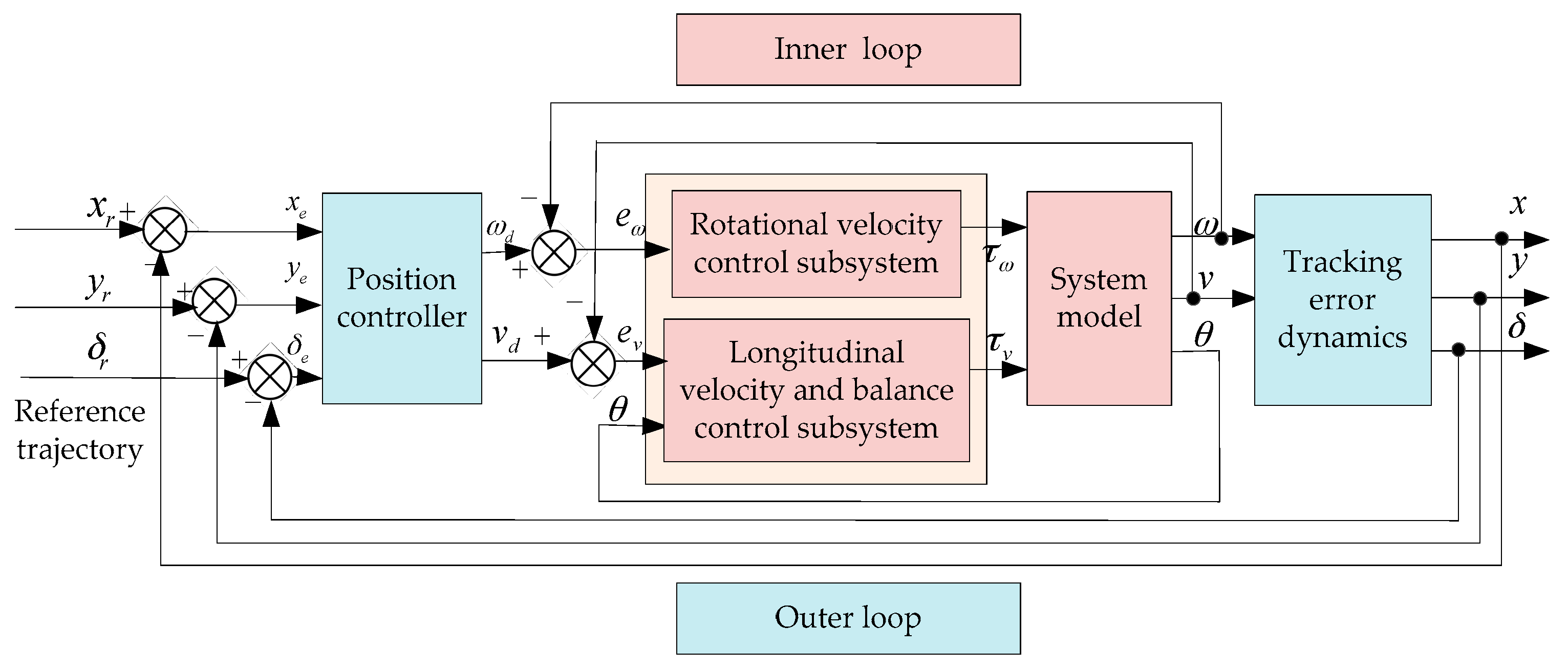
Section 3, inner and outer loop controllers are designed, and necessary stability considerations are discussed. Then the feasibility and effectiveness of the different control methods are compared by MATLAB simulation in
Section 4, followed by the conclusions in
Section 5. The configuration of an experimental set-up of the TWIP vehicle and the results are given in
Section 6.
3. System Description and Modeling
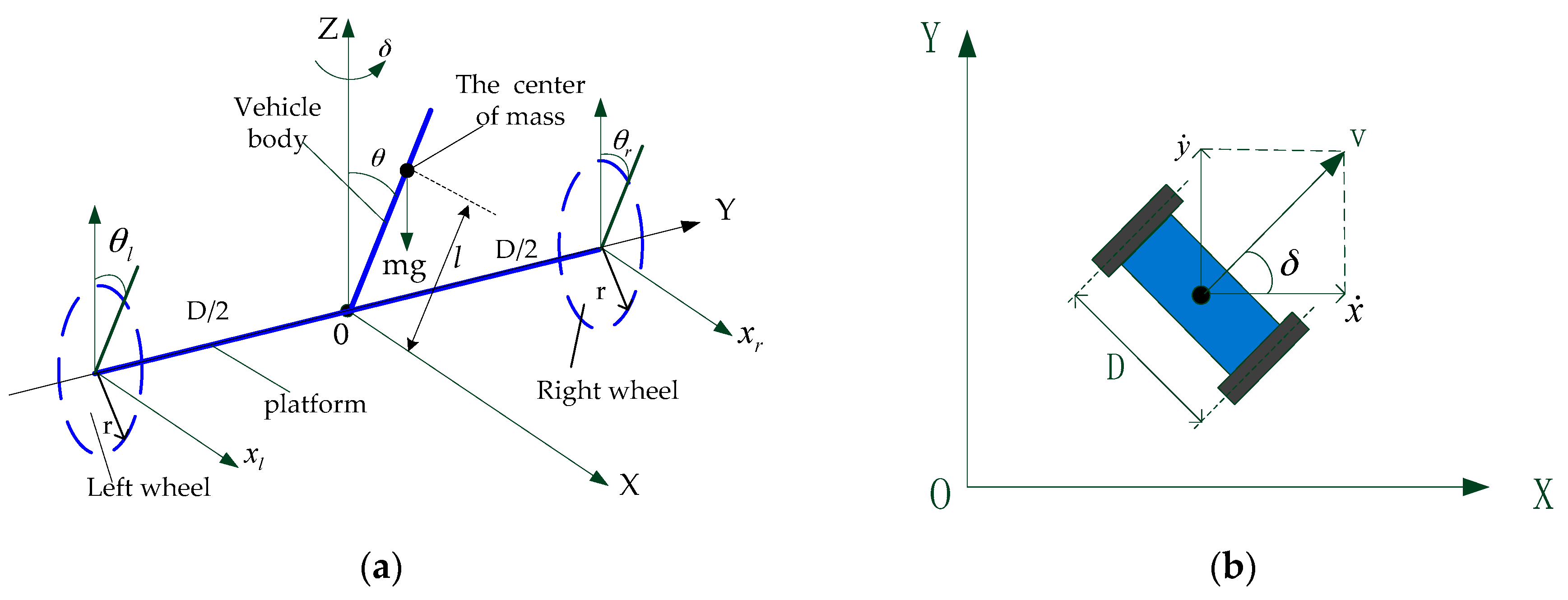
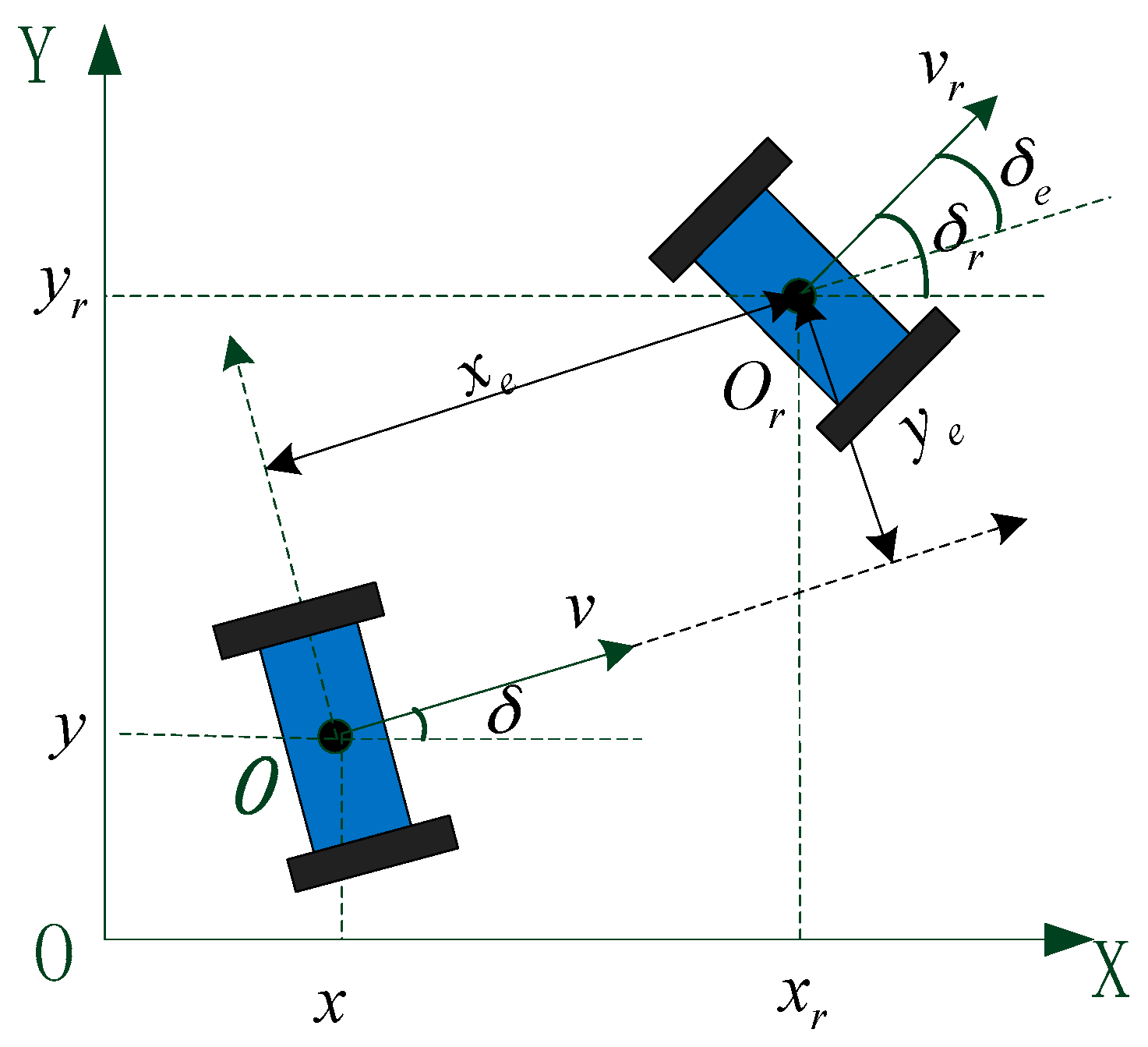
The motion of the TWIP vehicle is described under an inertial coordinate system. The simplified schematic diagram and the two-dimensional plan view of the vehicle are shown in
Figure 3.
The origin O of the fixed coordinate system OXY is the center of the axle, the positive direction of OX-axis is the forward motion of TWIP, OY-axis is coincident with the axle, the positive direction of OZ-axis is vertically upward. The parameters and variables of the system are shown in
Table 1. During the motion process of our two-wheeled vehicle, since there are only two points contacting with the ground, and the body has a motion similar to inverted pendulum motion, we can make a few assumptions in order to build dynamic model for the system:
- (1)
There exists sufficient friction between the wheels and the ground, which makes the system subject to non-holonomic constraints, i.e., the assumption of no sliding and skidding holds throughout.
- (2)
Take the TWIP vehicle as a perfectly rigid body, the distance from the center of mass of the body to the axle is ;
- (3)
The influence caused by the dynamic characteristics of DC motors is ignored;
- (4)
Ignore the effects caused by friction and damping force of bearings and revolute pairs to the motion state of the system.
In the paper, we adopt the Lagrange energy equation to build the kinematic model of the two-wheeled car. In order to eliminate the effect caused by the non-holonomic constraint, we choose
as the generalized coordinates system, then the kinematic model of the two-wheeled car can be written in the following form:
where,
denotes the inertia matrix,
is the vector of coriolis and centrifugal forces
is the vector of gravitational forces,
denotes the matrix of control coefficients,
is the vector of control inputs.
Defining a new velocity vector
, then the relationship between a new coordinate vector
and the generalized coordinate vector
can be written as follows:
Then the dynamics of the system can be formulated as follows:
where:
In order to simplify the controller design, the state-space equations can be derived from (3):
where:
is known as the system state. is the system control input, and , .
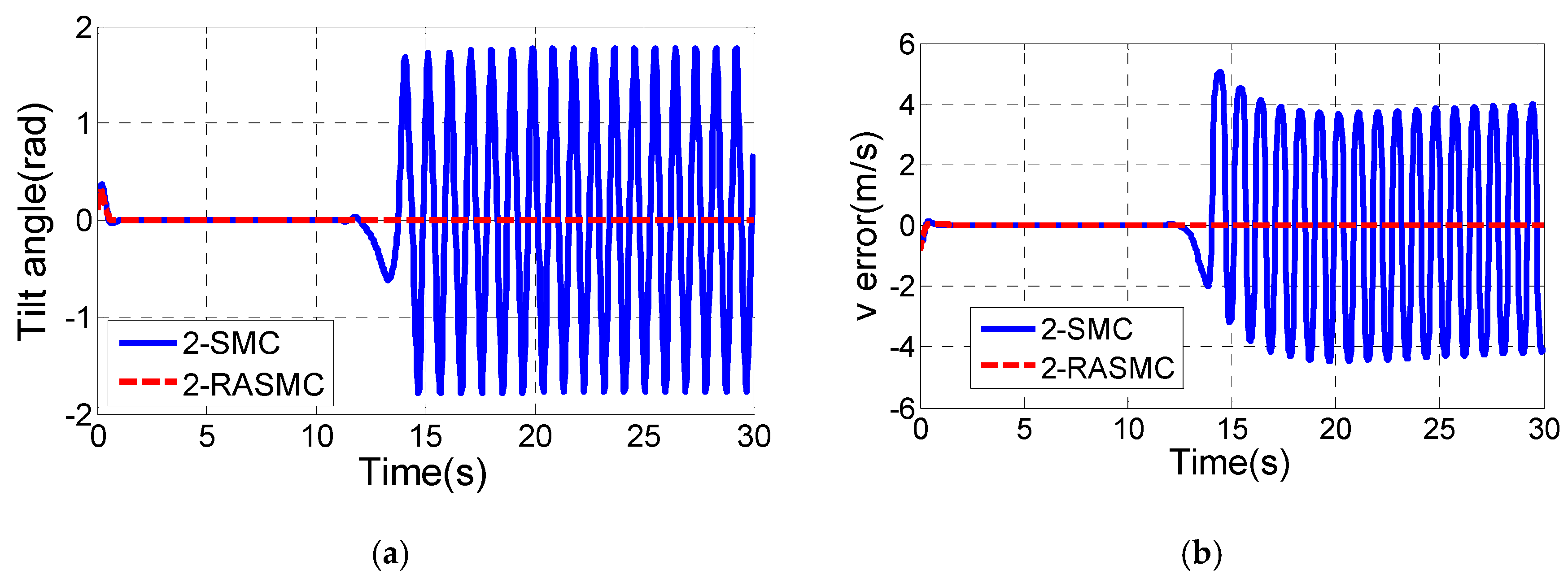
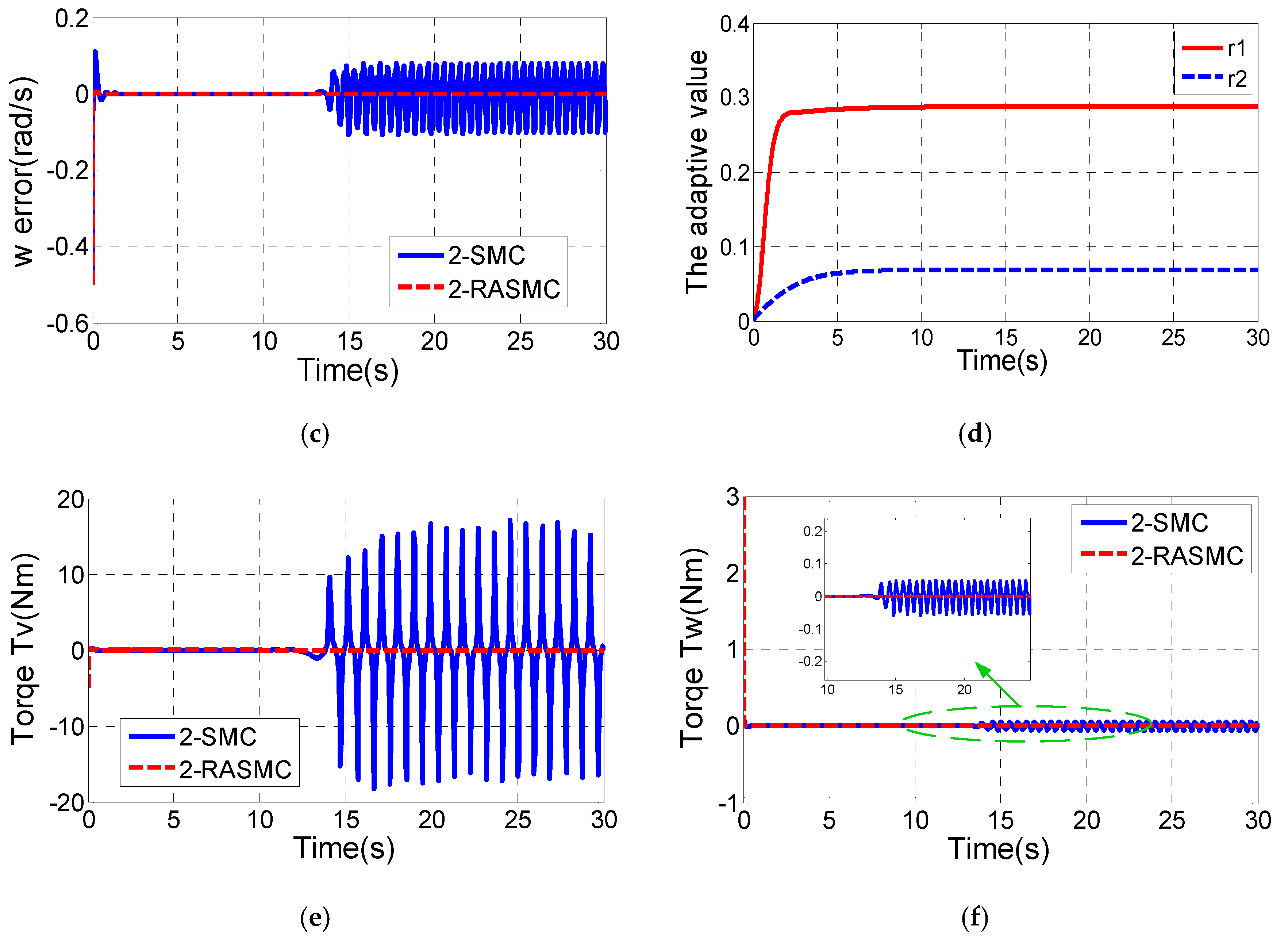
5. Simulation and Discussion
In this section, a lot of comparative simulations have been done to verify the validity of the proposed control methods. We have done a lot of simulations and found the appropriate control parameters of the designed outer loop controller as shown in
Table 4.
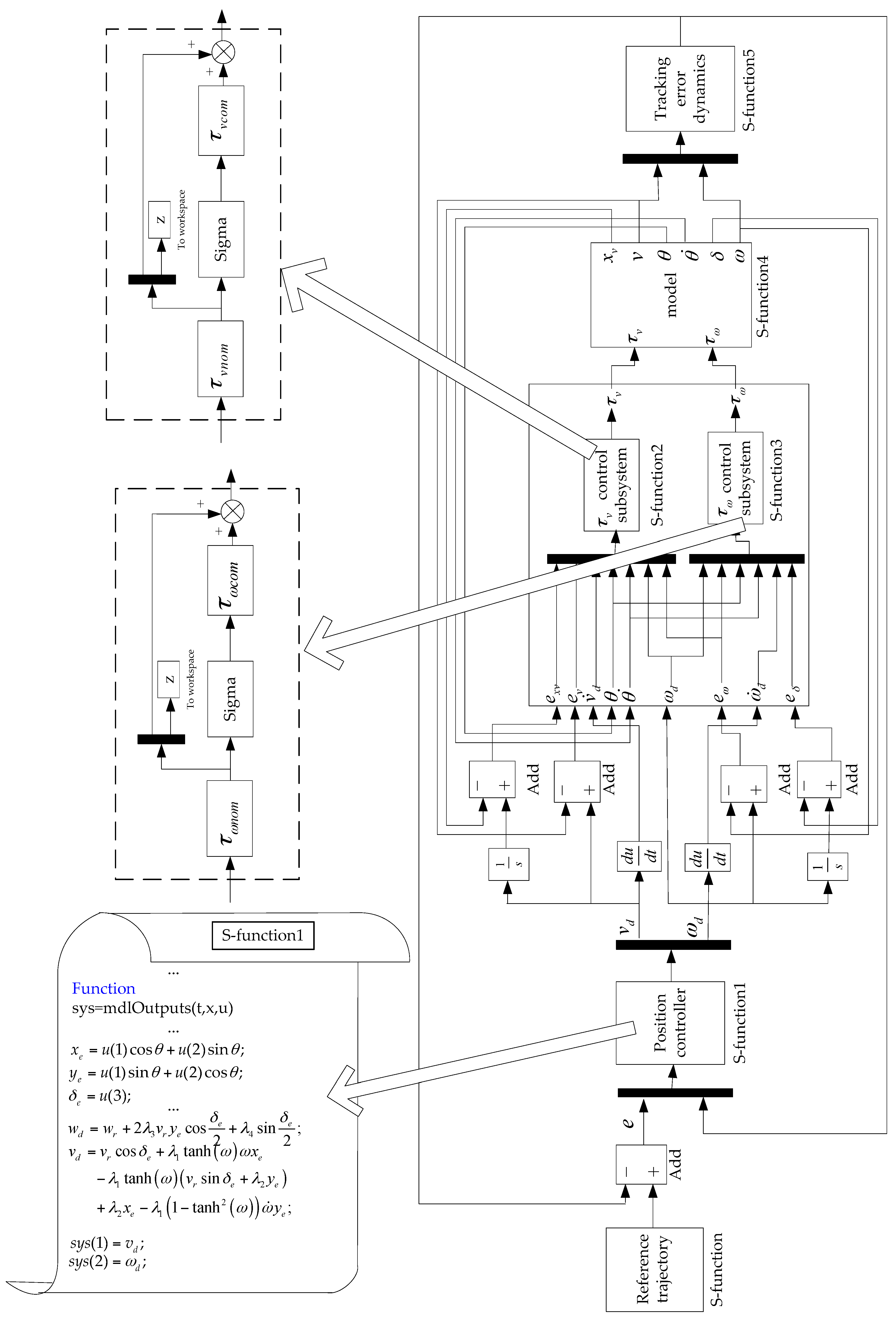
Table 5 exhibits several different algorithmic approaches combined by diverse control methods of inner and outer loop controllers. The simulation framework for 2S-B controller is shown in
Figure A1 of the
Appendix.
The control parameters of the PID controller used for comparison in this paper are settled by the Ziegler-Nichols method and shown in
Table 6.
First, a reference circular trajectory with
rad/s,
m/s is given and the radius of the desired trajectory
is 1 m. Furthermore, we assume that the vehicle start point is
, and the initial state variables are supposed as
.
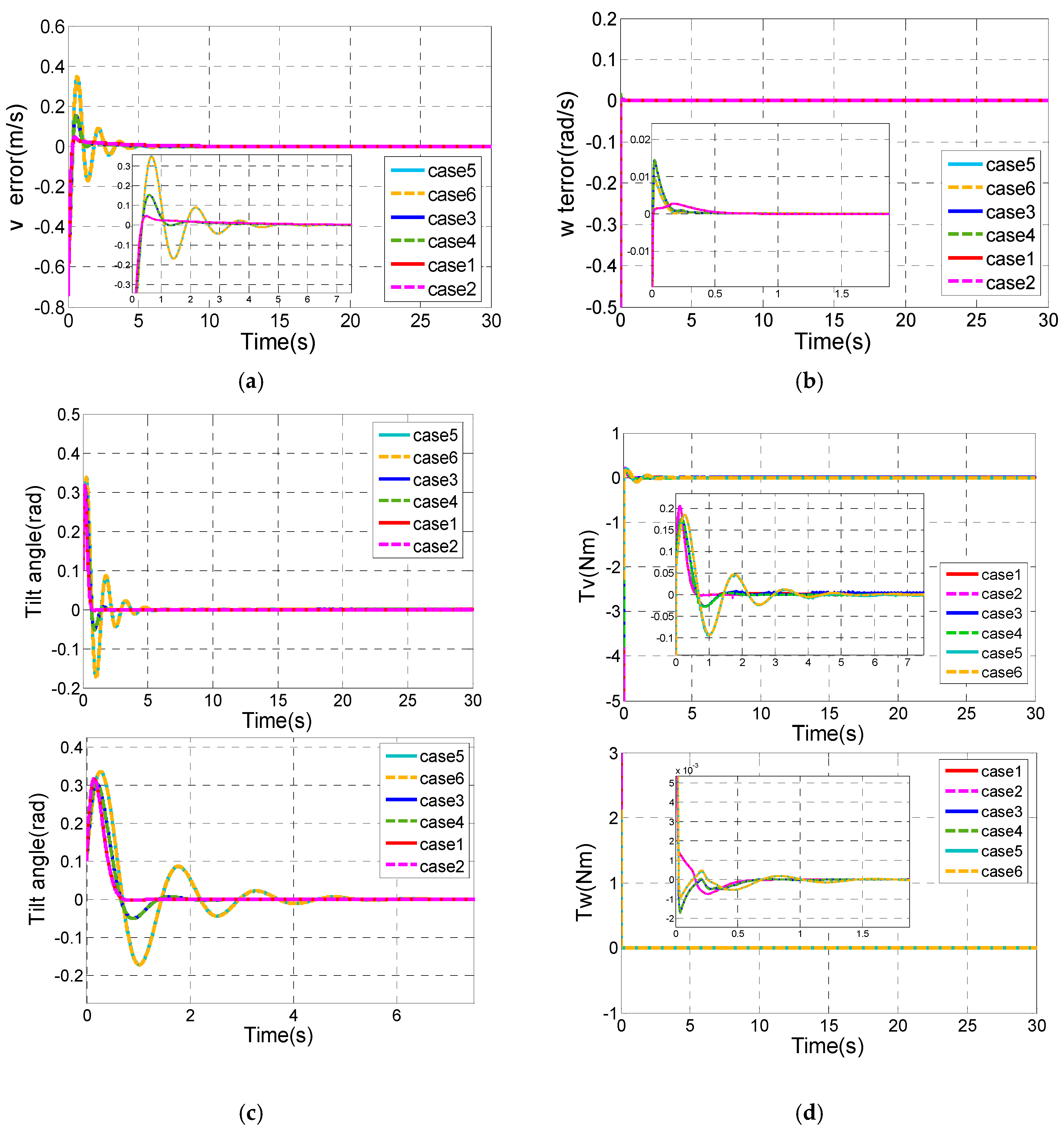
Figure 10 shows the practical tracking for the circle mentioned above with six different control combinations.
From
Figure 10a, it is clearly shown that the 2S-B controller has the shortest settling time of the tilt angle (about 1.55 s), while the worst settling time of the tilt angle is about 7.06 s in the P-D controller. The tracking error of x decreases to zero after t = 0.95 s by the 2S-B controller. When it comes to the P-D controller, the tracking error of x has the longest settling time of 4.44 s (
Figure 10d). Moreover, the overshoots of θ and
in the 2S-B controller are smallest among them.
Figure 10d indicates that the DMLF method has better response about the tracking error of δ, but worse performances of
and
than the backstepping method. Considering these simulation results, the 2S-B controller is the most effective control combination strategy.
To further verify the effectiveness of the proposed controllers, a more sophisticated trifolium trajectory is used as a reference trajectory.
A trifolium trajectory can be designed as , . Here, the desired length of each leaf ρ is chosen as ρ = 5, = 0.05. Then, the reference longitudinal velocity and the reference rotational velocity can be calculated in prior. Furthermore, we assume that the vehicle start point is , and the initial state variables are the same as that of tracking a circle.
The system states are divergent for tracking a trifolium trajectory using the P-D controller and P-B controller. The reason why it diverges is the error of the longitudinal velocity
converges more slowly than the acceleration of the reference longitudinal velocity
. Moreover, the simulation results are shown in the
Appendix A.
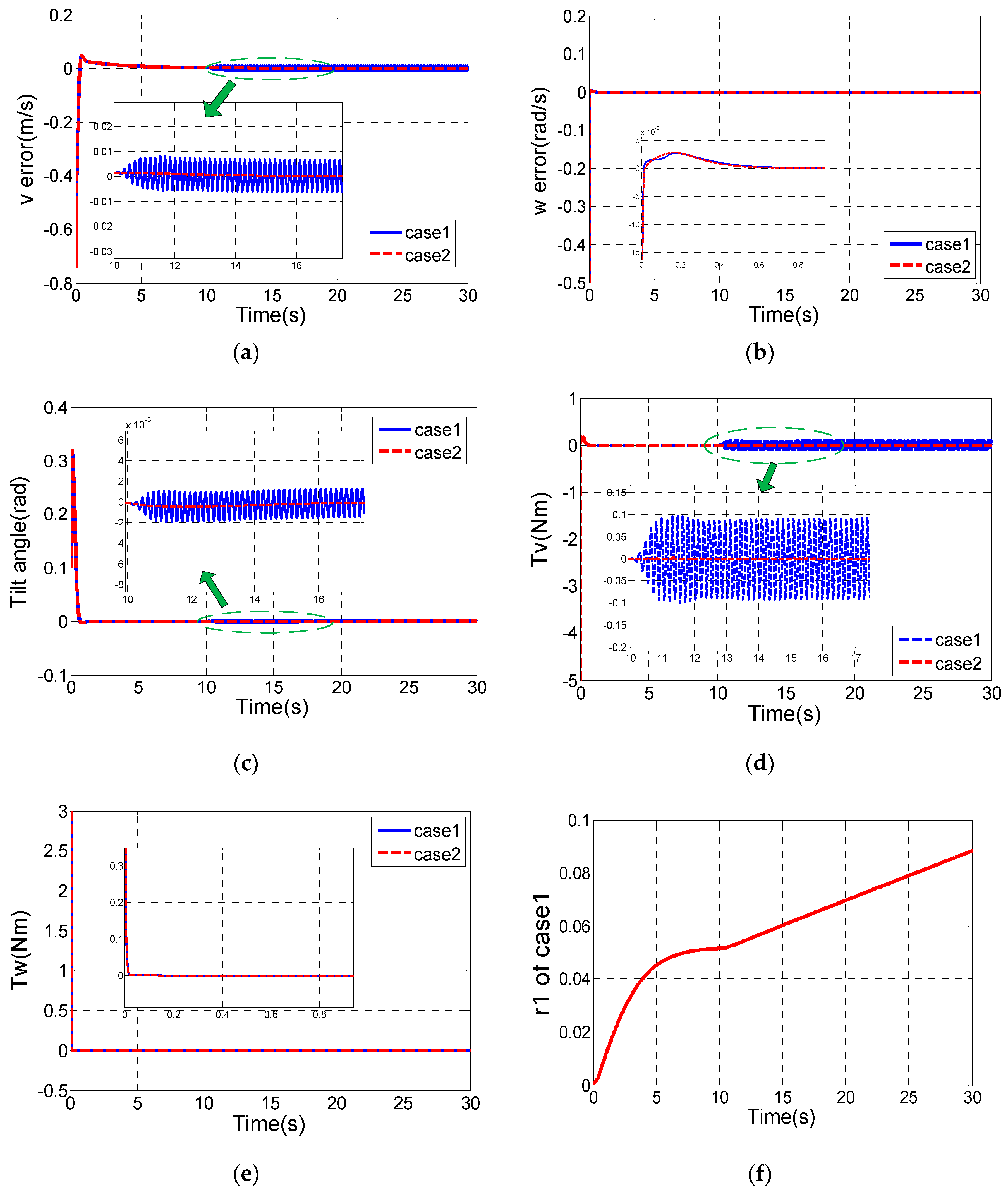
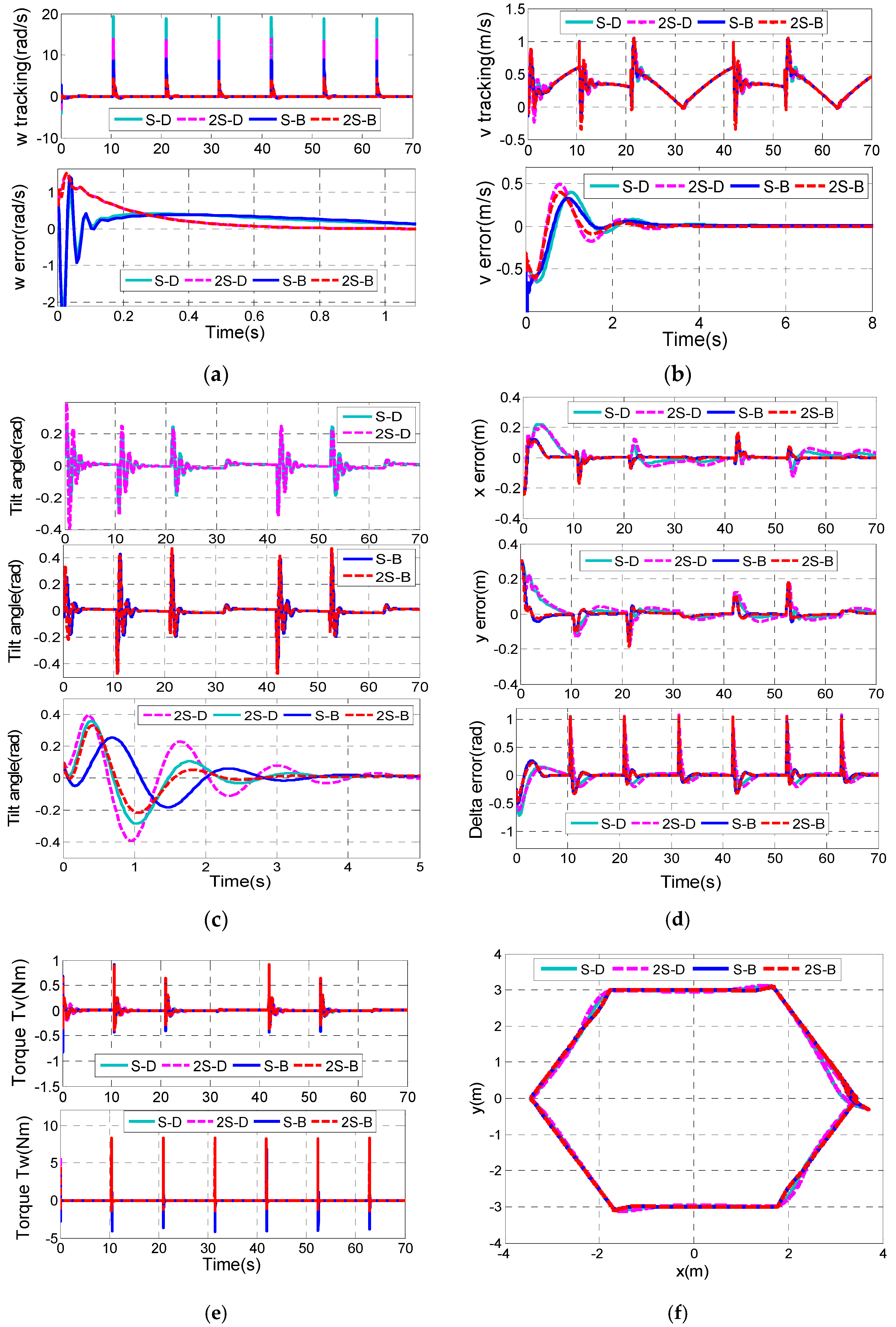
Figure 11 shows the comparison information of the four remaining control combinations, S-D controller, 2S-D controller, S-B controller and 2S-B controller.
It is clearly shown in
Figure 11a that the S-D controller has the shortest settling time of the tilt angle (about 2.3 s), while the longest settling time of the tilt angle is about 4.37 s in the S-B controller. In
Figure 11e, S-D and 2S-D have high rotational control torque
up to around 20 Nm, while the rotational control torque
in S-B controller is smaller than 2 Nm. The tracking errors of x and y are much smaller in the S-B controller and 2S-B controller than those of the S-D controller and 2S-D controller (
Figure 11d). Moreover, the overshoots of
and
in the 2S-B controller are smallest among them.
Finally, a hexagon trajectory, which contains an abrupt variation of longitudinal velocity and rotational velocity, is more difficult to track than the trifolium one. The hexagon trajectory we adopt is described by piecewise linear functions. Furthermore, assume that the vehicle start point is , and the initial state variables are set as .
Similarly, the system states are divergent for tracking a hexagon using P-D controller and P-B controller. Moreover, the simulation results are shown in the
Appendix A.
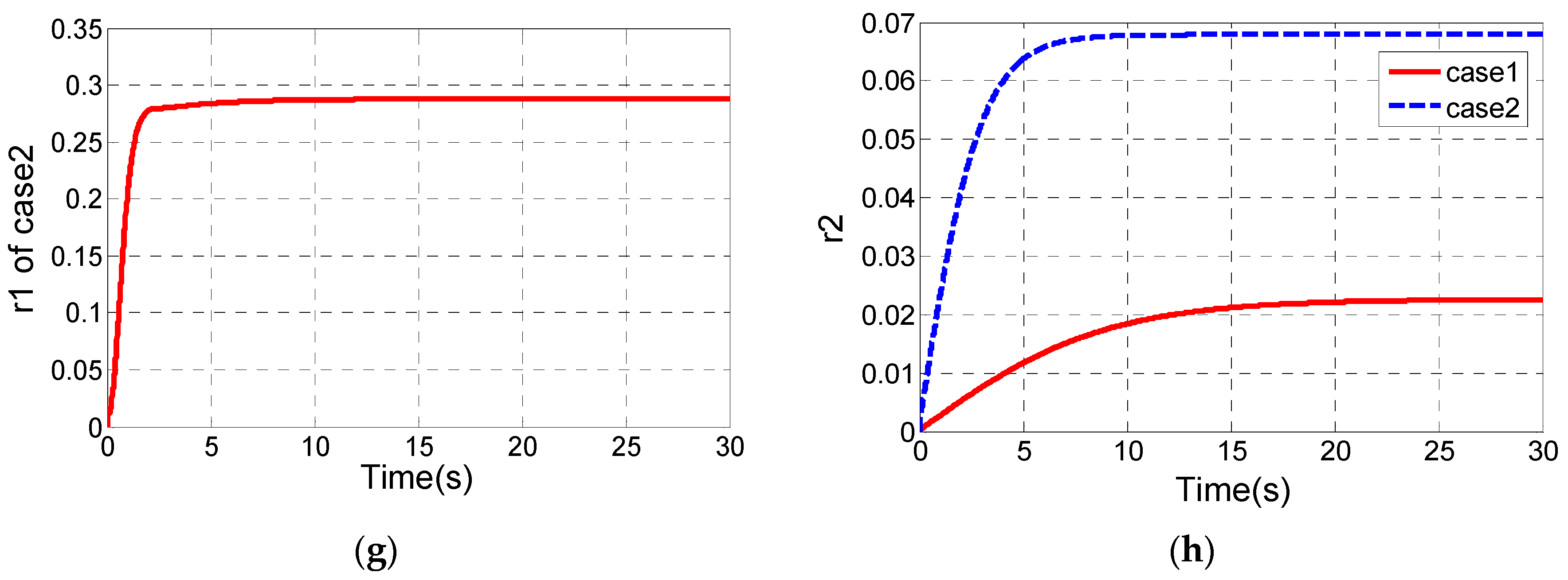
Figure 12 shows the practical tracking performances for the hexagon mentioned above with four different control combinations.
Figure 12c shows that the 2S-B controller has the shortest settling time of the tilt angle (about 2.3 s), while the longest settling time of the tilt angle is about 3.3 s in the S-D controller. The tracking errors of x and y decrease most quickly to zero in the 2S-B controller. When it comes to the S-D controller and 2S-D controller, the settling time of
and
is up to about 7 s (
Figure 12d). Moreover, the overshoots of
,
and
in the 2S-B controller are the smallest.
Although the hexagon trajectory seems to be tracked effectively, the torque performance is actually terrible due to the abrupt variation of the trajectory of longitudinal velocity and rotational velocity, and this situation is undesirable in practice.
Table 7 shows the different control effects of the six control combinations, such as the overshoot and the settling time of θ,
,
,
, and a coincidence factor indicator (CFI) which illustrates the trajectory tracking performance.
We define a coincidence factor indicator (CFI) to describe the tracking performance. The CFI is obtained as follows:
where, ()* means the normalization of expressions in brackets, min is the minimum of
from
i = 1 to
i =
N, max is the maximum of
from
i = 1 to
i =
N,
is the number of samples, and T is the total time of simulation.
Different control effects of the six control combinations are clearly shown in
Table 7, where we can see that the P-D and the P-B controller have poor adaptability to different trajectories. The convergence rates of
,
and
are much faster by using the backstepping method than using the DMLF method. It can be clearly seen that 2S-B method has the best CFI as well as shortest settling time of the tilt angle for all three trajectories, so it can be concluded that among the six control combinations, 2S-B controller has the best control performance for its fast convergence speed, small overshoot and best trajectory coincidence.
6. Experimental Results
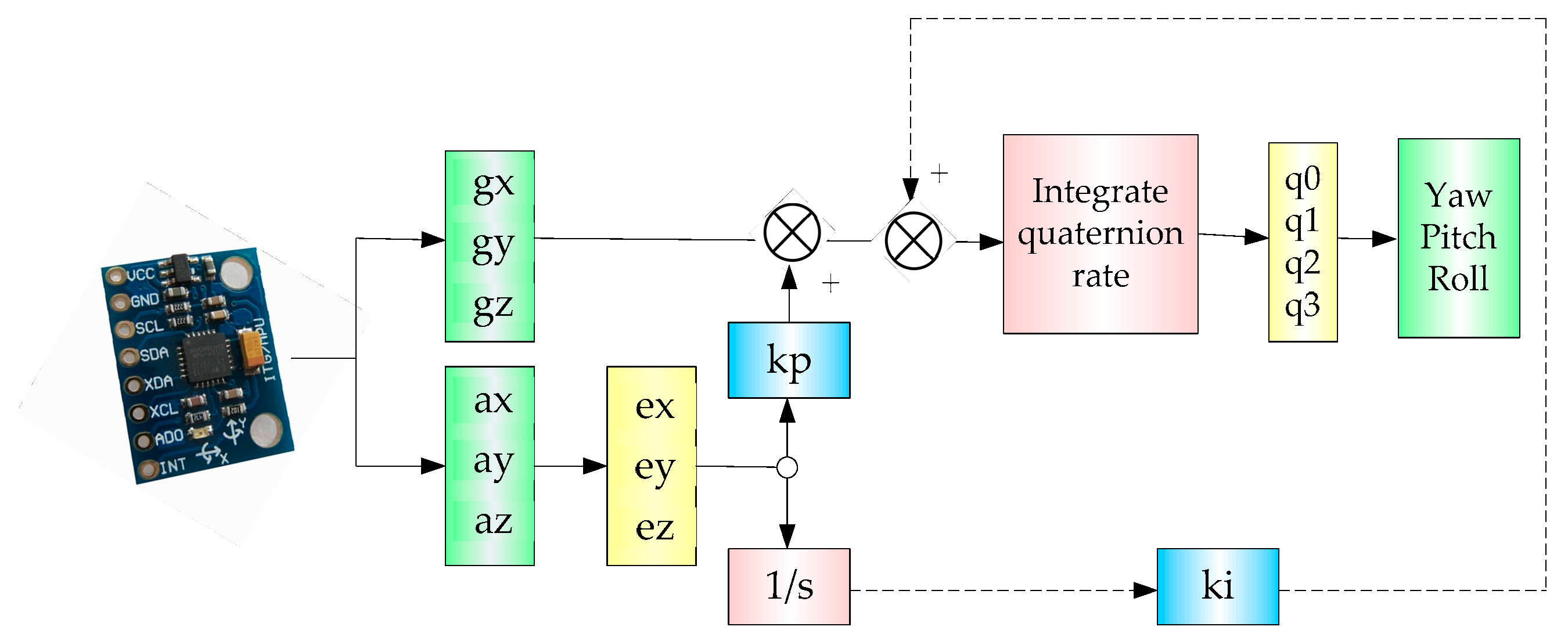
Since the sensor (MPU-6050) has an embedded 3-axis MEMS gyroscope and a 3-axis MEMS accelerometer, we need to utilize an information fusion algorithm to obtain relatively accurate information.
Figure 13 shows the frame of the complementary filter for information fusion.
The attitude data of the TWIP vehicle is measured via the onboard IMU, the velocity data is measured by two rotary encoders, and the location information of the TWIP vehicle is measured by the UWB positioning technology just as shown in
Figure 2. The placement of anchors in space is shown in
Figure 14.
The position of the Tag can be expressed as follows:
To verify the tracking performance of the proposed design, an indoor tracking test was implemented. The desired trajectory was set to be a circle with
rad/s,
m/s. The radius of the desired trajectory
was 1 m. Considering the existence of mismatch between the real-time system model and the mathematical model, the feedback gains obtained from simulations may not function well on the real-time platform, thus the control design parameters need to be adjusted through experiments on the prototype. In practice, we use the control design parameters as
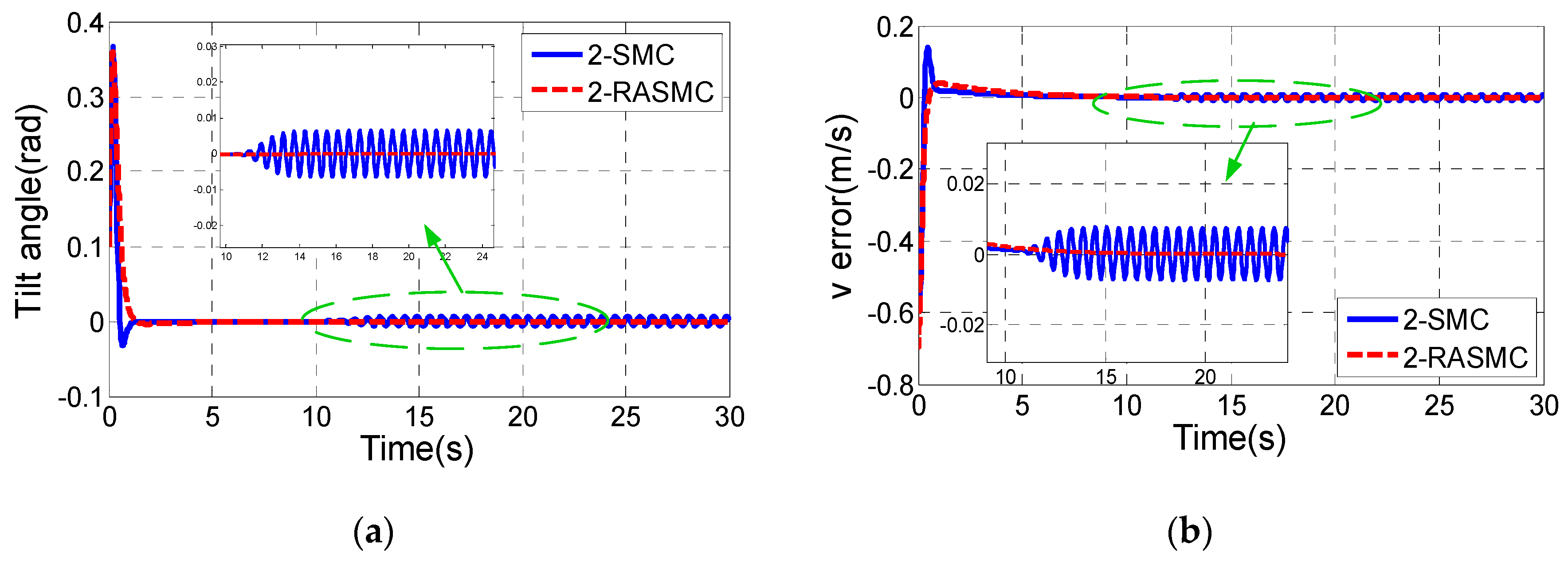
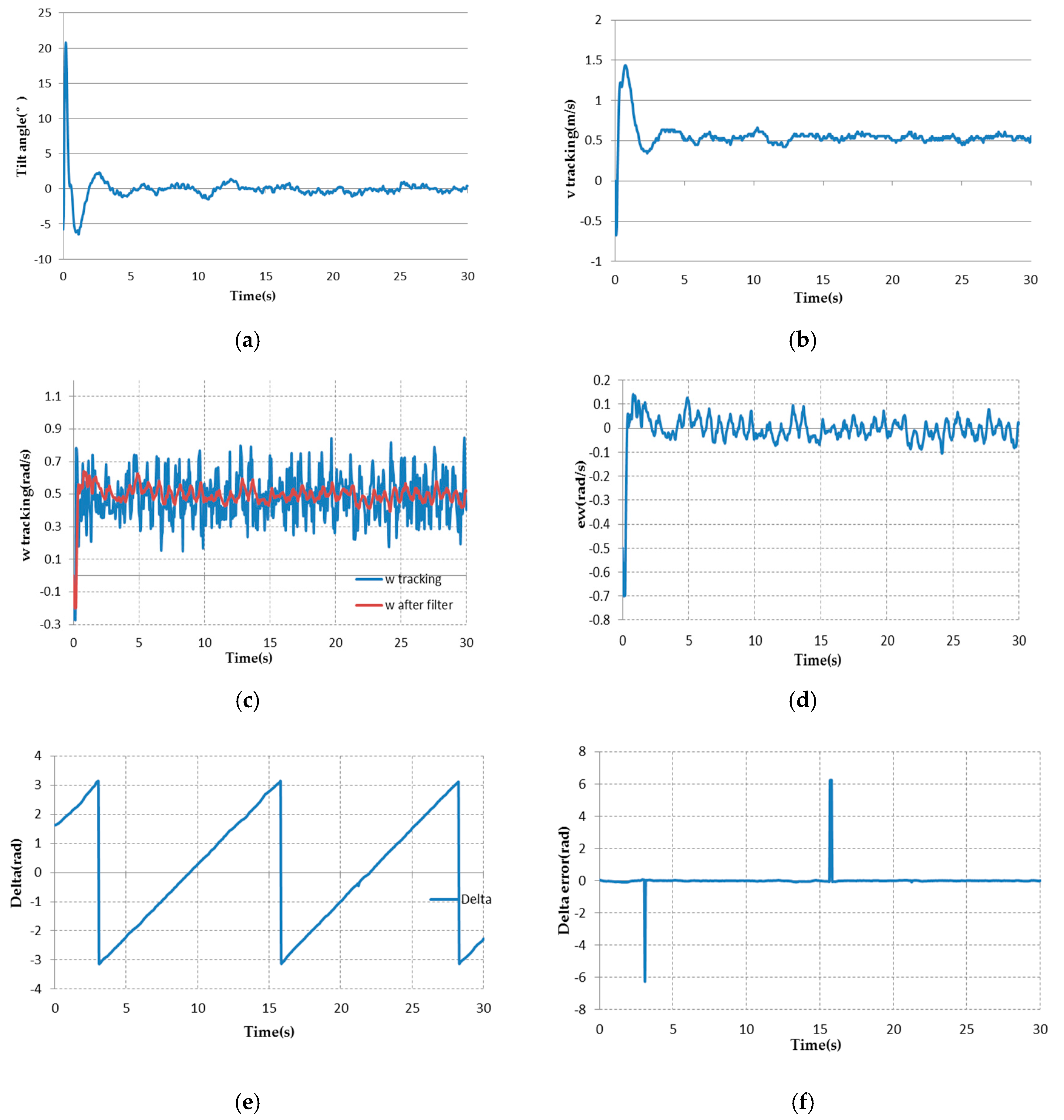
Figure 15 shows the indoor experimental results using the 2S-B controller for tracking the circle.
After the battery is fully charged, the TWIP vehicle can run continuously for about 30 min. The test of tracking a circle lasts about 30 s, and the TWIP vehicle finished the trajectory tracking for more than two rounds.
Figure 15a shows the tilt angle of the TWIP vehicle.
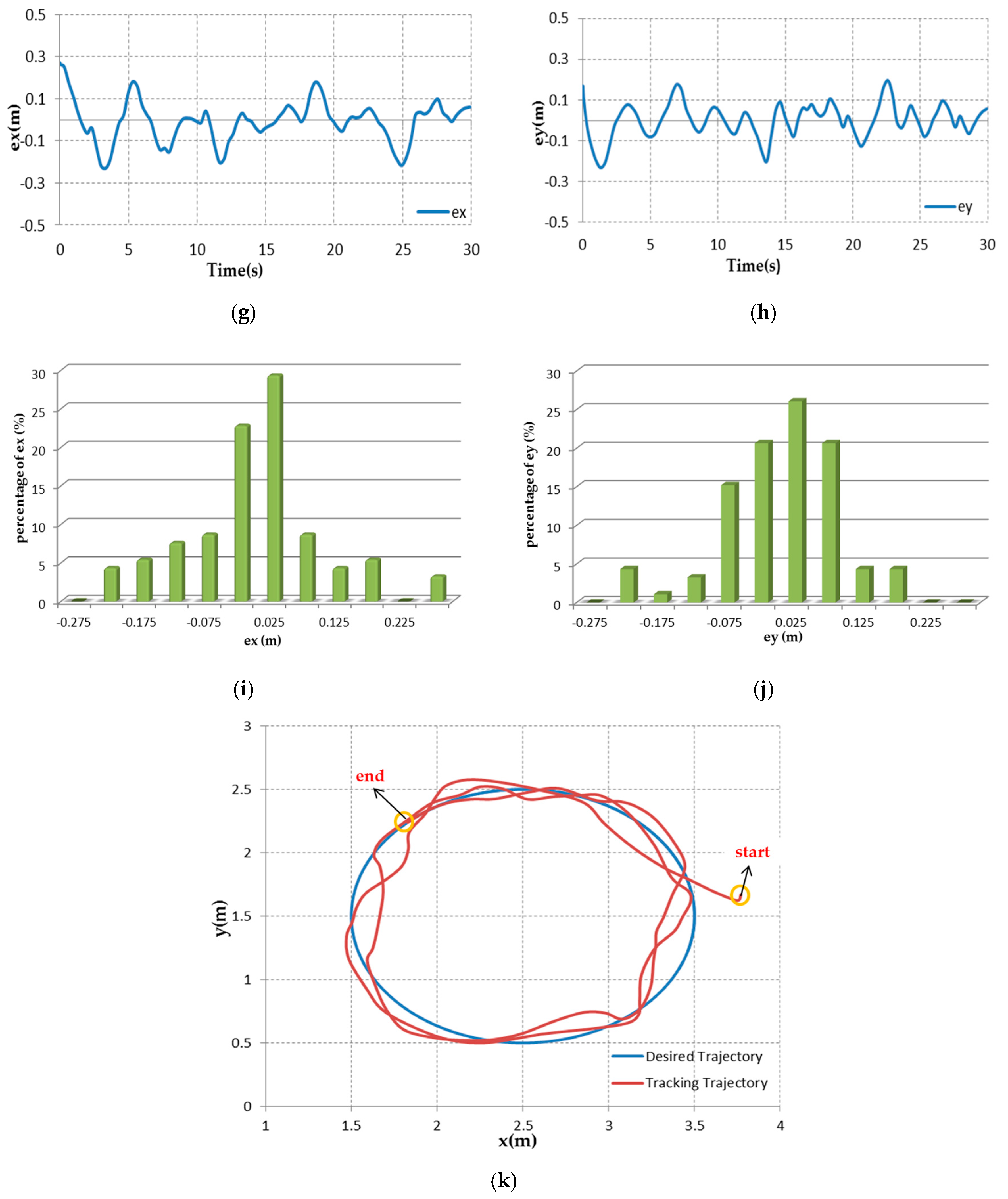
Figure 15g,h shows the position tracking errors. Because there is a cm-level measure error in the position measurement by UWB technology, the position tracking errors cannot converge to zero. The maximum position tracking error is about ±0.27 m for x-direction and about ±0.23 m for y-direction, but more than 80% of the all recorded horizontal points remain in a circle with a radius of 0.1 m. The RMS value of the position error is 0.1036 m in x-direction, and 0.0841 m in y-direction. The settling time of the tilt angle is about 3.5 s. Td the tilt angle is controlled within ±1.5°. This demonstrates the good tracking performance achieved in the indoor environment.