An Artificial Bee Colony-Based Green Routing Mechanism in WBANs for Sensor-Based E-Healthcare Systems
Abstract
1. Introduction
2. Related Works
3. Network Model
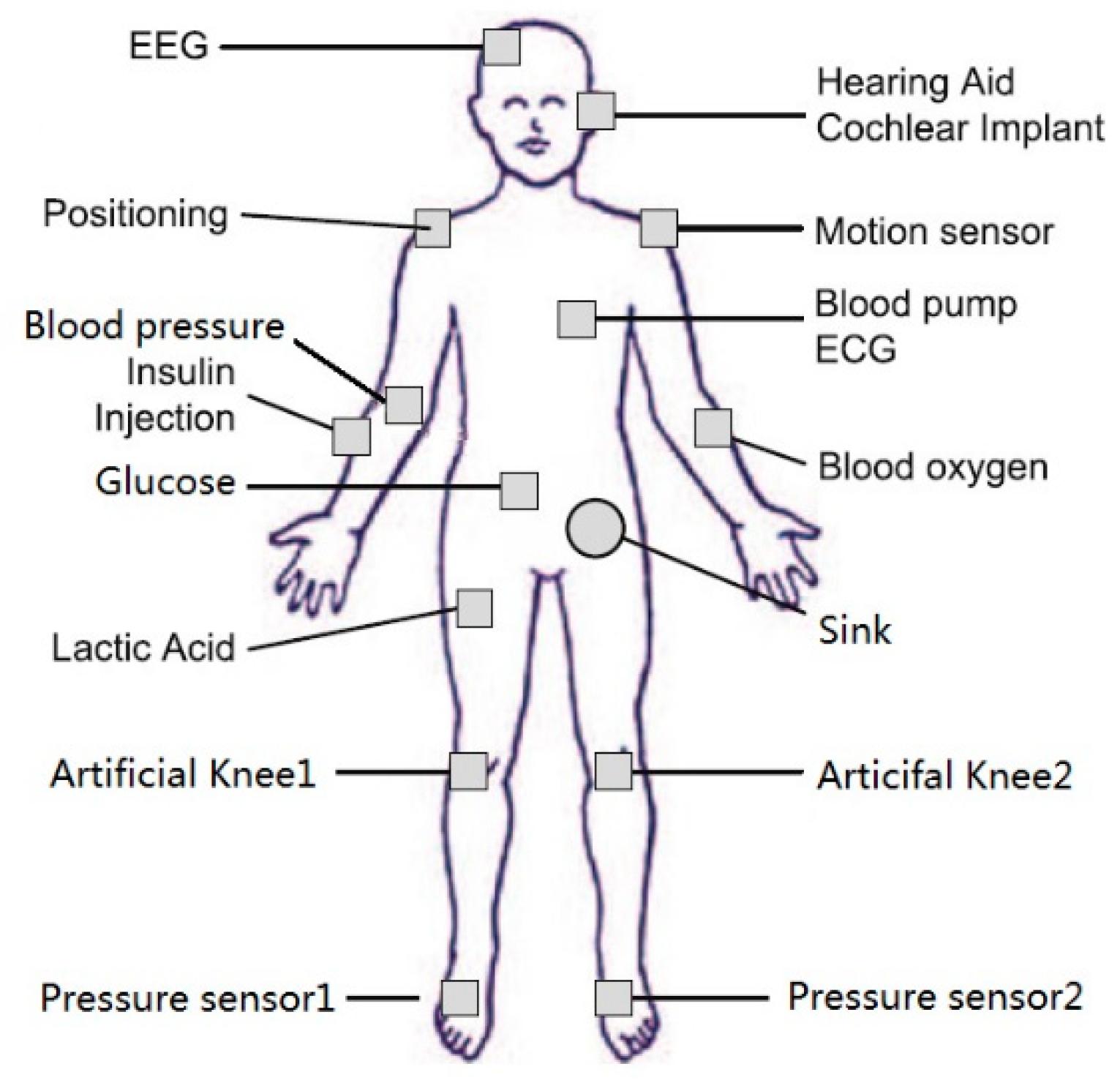
3.1. Mathematical Description of WBANs
3.2. The Important Level Factor α
4. The Optimal Path of Energy Consumption (OPEC)
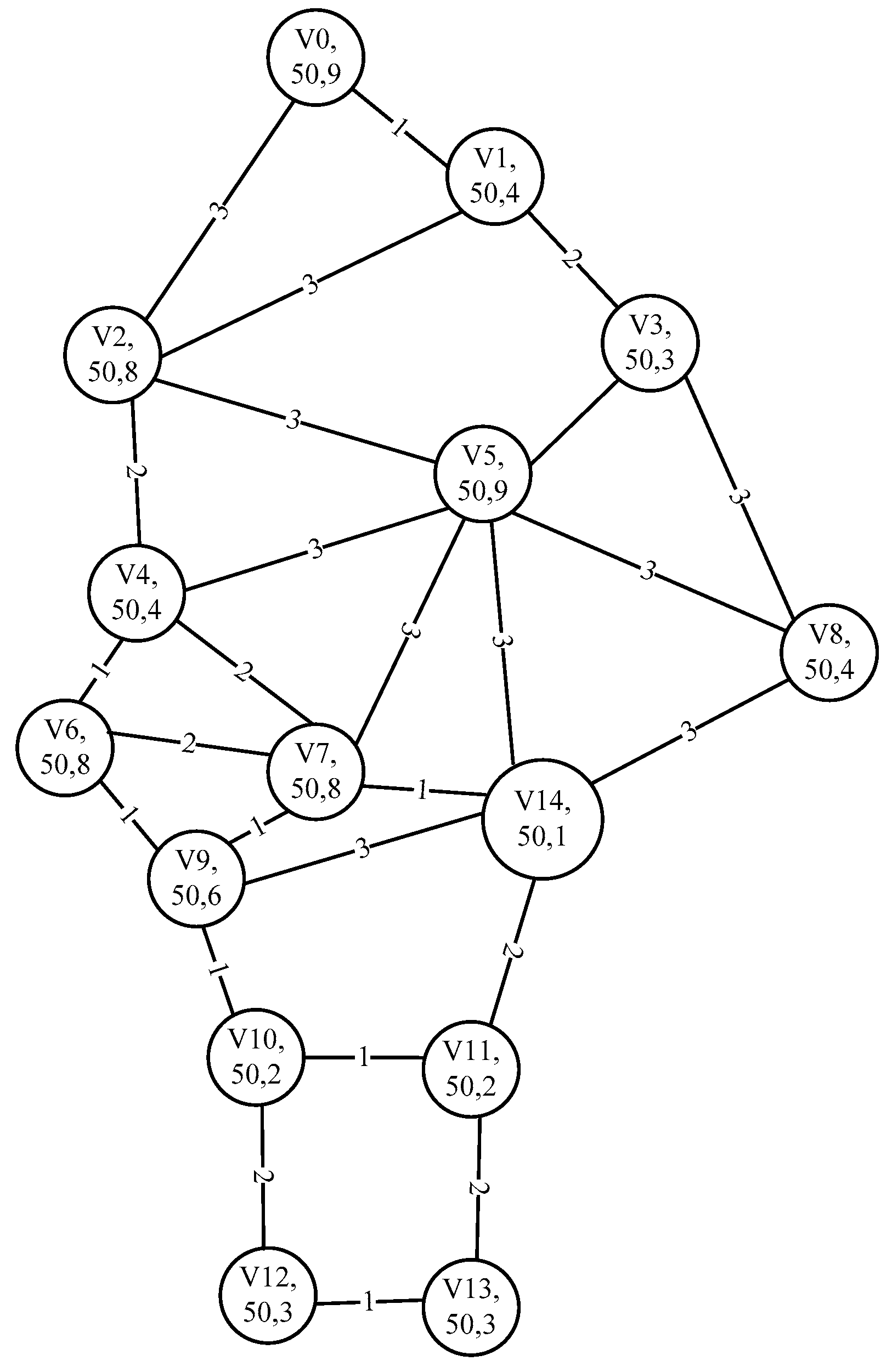
4.1. Mathematical Description of Path Energy Consumption
4.2. Definition of the OPEC
5. Introduction to the Artificial Bee Colony (ABC) Algorithm
6. The Optimal Energy Consumption Artificial Bee Colony-Based WBAN (OEABC)
6.1. The Fitness Function of the Path
6.2. Initial Path Generation Formula
6.3. The Generation Formula of the New Path
| Algorithm 1. OEABC Algorithm |
| Input: Network topology, starting point, end point Output: Optimal energy consumption path
|
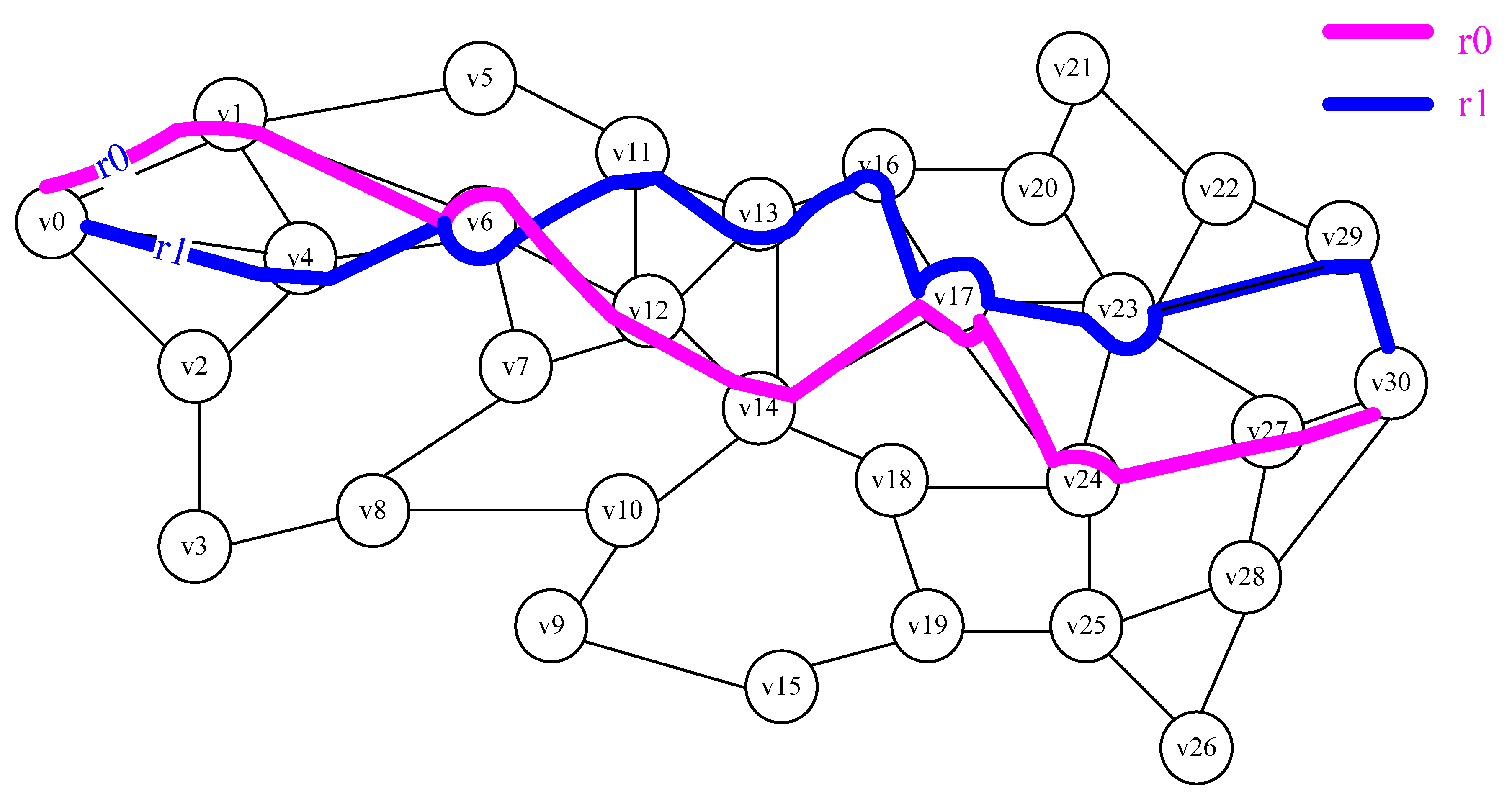
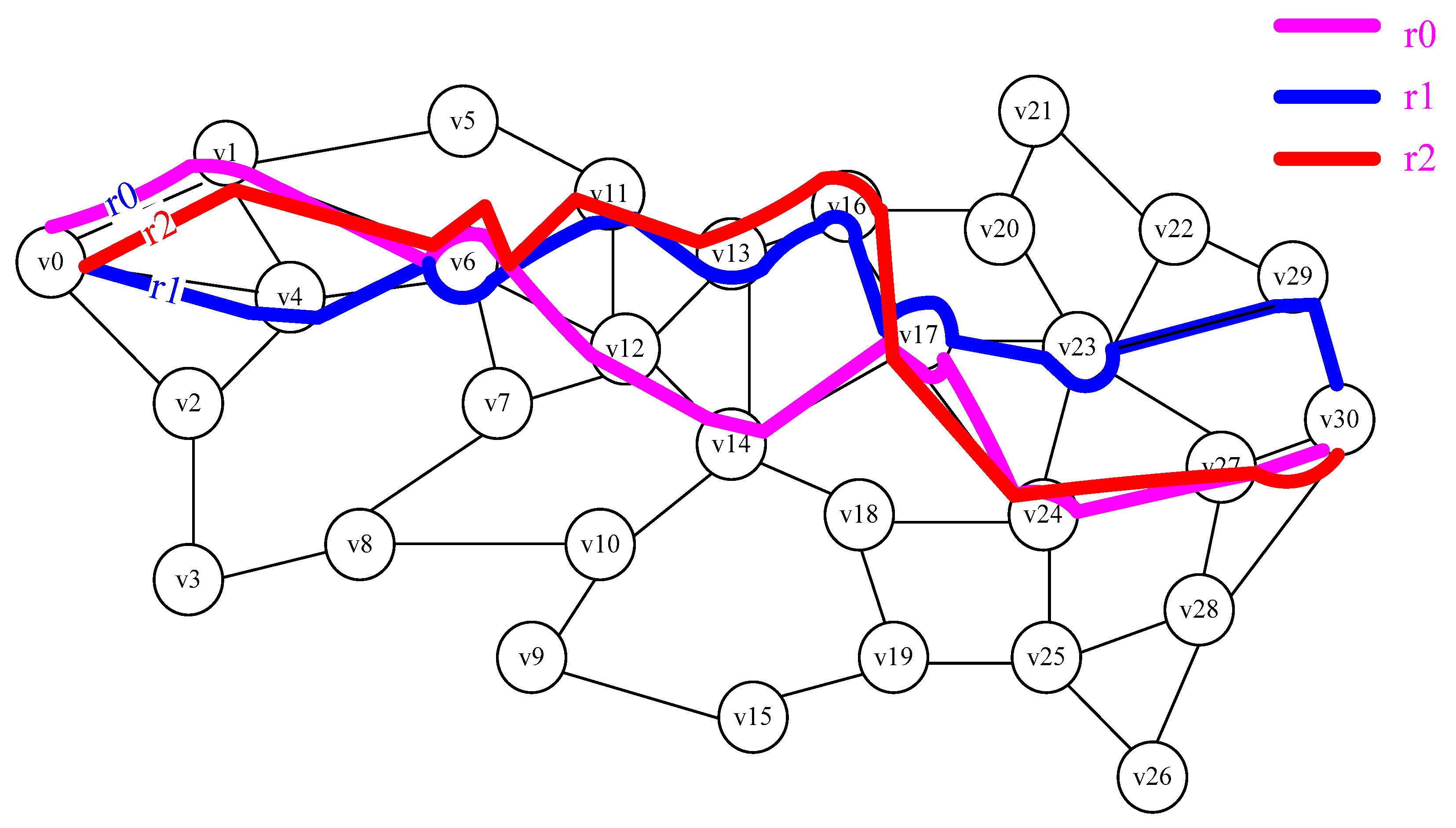
7. Experiments and Results Analysis
7.1. Fitness Analysis of the Path
7.2. Parameter Analysis
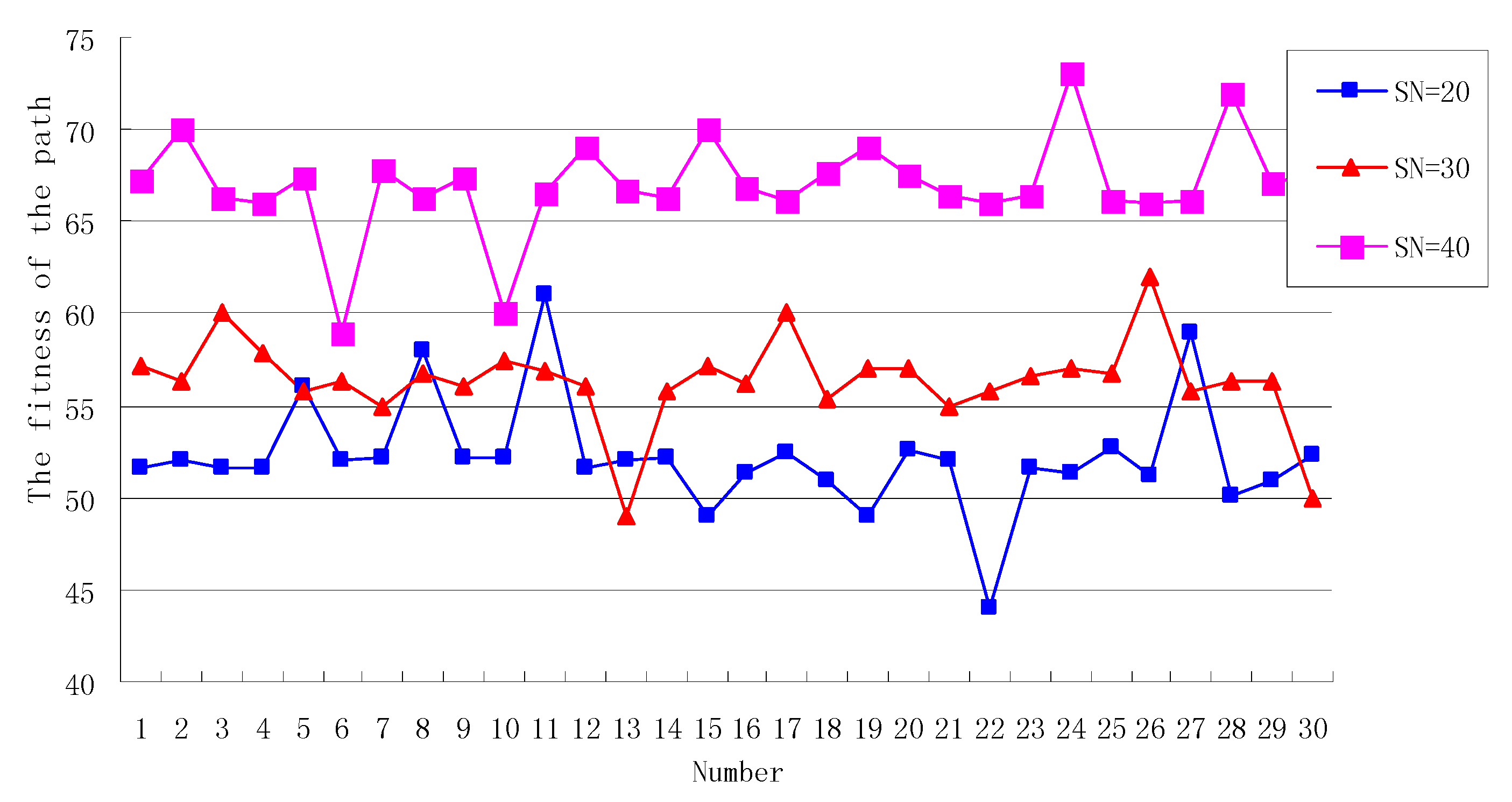
7.2.1. The Analysis of SN
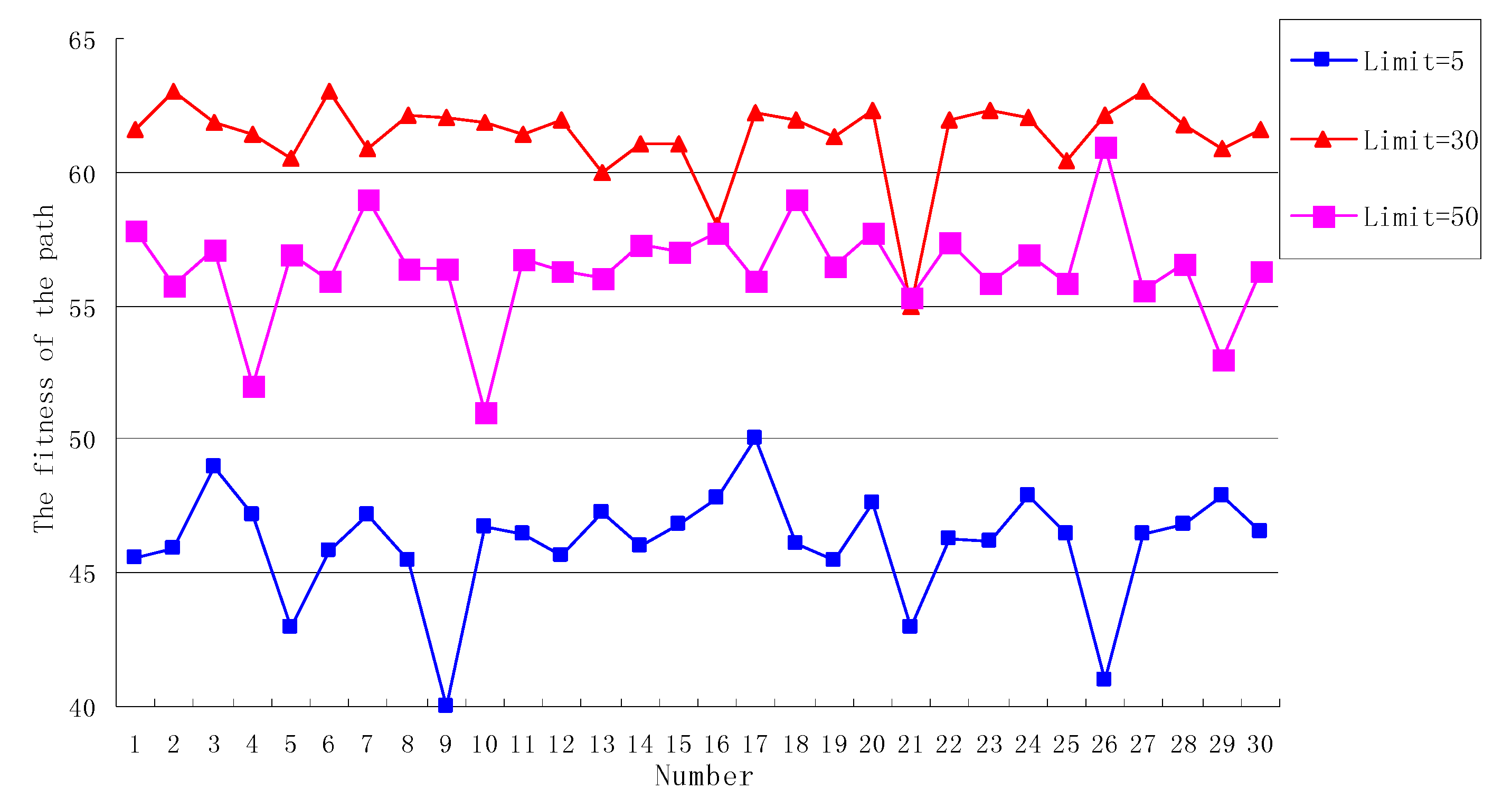
7.2.2. The Analysis of Limit
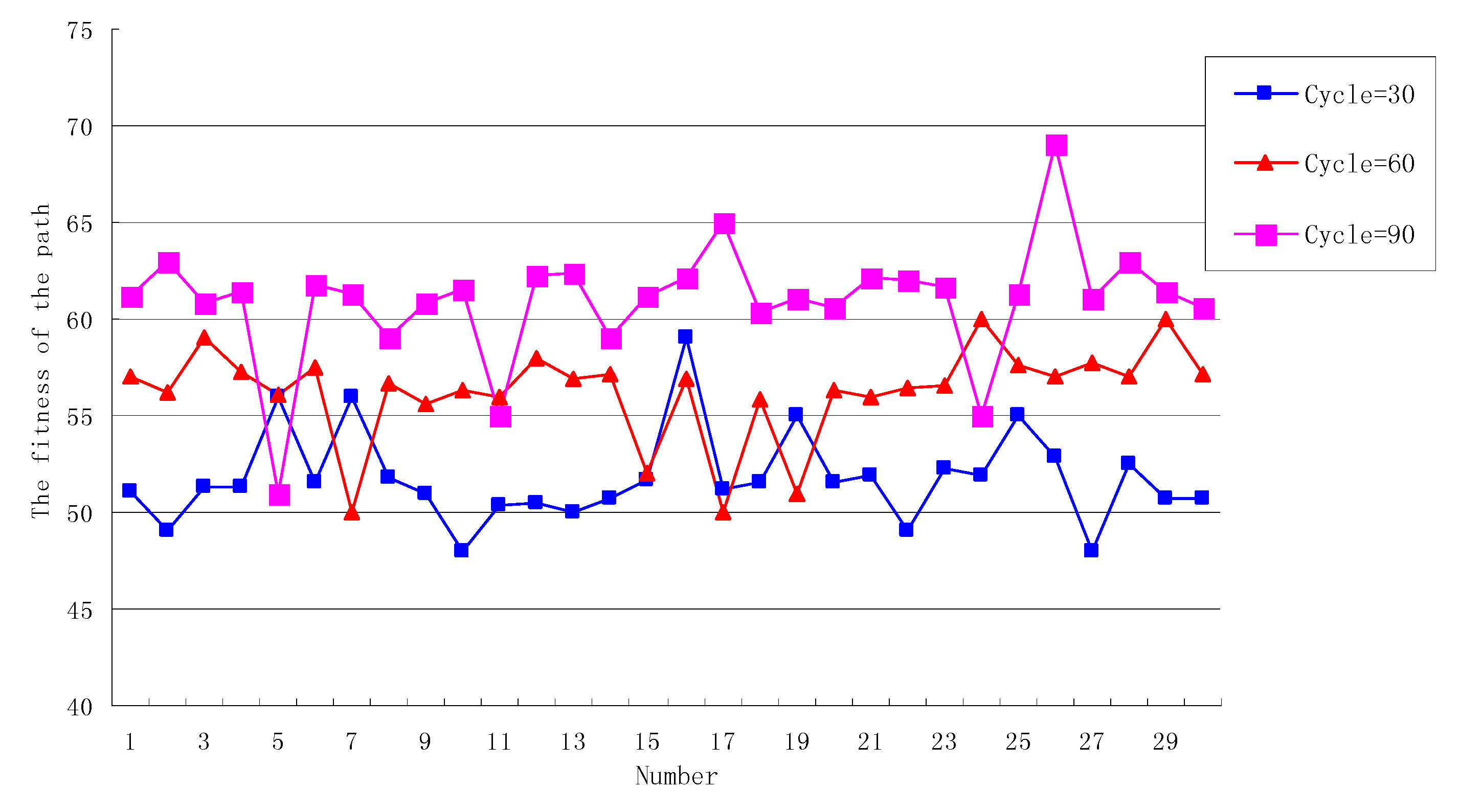
7.2.3. The Analysis of Cycle
7.3. Comparative Analysis
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- IEEE. IEEE Standard for Local and Metropolitan Area Networks—Part 15.6: Wireless Body Area Networks; IEEE Std.: Piscataway Township, NJ, USA, 2012; pp. 1–271. [Google Scholar]
- Otto, C.; Milenkovi, A.; Sanders, C.; Jovanov, E. System architecture of a wireless body area sensor network for ubiquitous health monitoring. J. Mob. Multimed. 2006, 1, 307–326. [Google Scholar]
- Hanson, M.A.; Powell, H.C.; Barth, A.T.; Ringgenberg, K.; Calhoun, B.H.; Aylor, J.H.; Lach, J. Body Area Sensor Networks: Challenges and Opportunities. Computer 2009, 42, 58–65. [Google Scholar] [CrossRef]
- Patel, M.; Wang, J. Applications, challenges, and prospective in emerging body area networking technologies. IEEE Wirel. Commun. 2010, 17, 80–88. [Google Scholar] [CrossRef]
- Ning, Z.; Xia, F.; Hu, X.; Chen, Z.; Obaidat, M.S. Social-oriented adaptive transmission in opportunistic Internet of smartphones. IEEE Trans. Ind. Inform. 2017, 13, 810–820. [Google Scholar] [CrossRef]
- Scanlon, W.G.; Conway, G.A.; Cotton, S.L. Antennas, propagation considerations for robust wireless communications in medical body area networks. Proc. IET Semin. Antennas Propag. Body Cent. Wirel. Commun. 2007, 11803, 37. [Google Scholar]
- Kiourti, A.; Nikita, K.S. A Review of Implantable Patch Antennas for Biomedical Telemetry: Challenges and Solutions [Wireless Corner]. IEEE Antennas Propag. Mag. 2012, 54, 210–228. [Google Scholar] [CrossRef]
- Quwaider, M.; Biswas, S. DTN routing in body sensor networks with dynamic postural partitioning. Ad Hoc Netw. 2010, 8, 824–841. [Google Scholar] [CrossRef] [PubMed]
- Tachtatzis, C.; Franco, F.D.; Tracey, D.C.; Timmins, N.; Morrison, J. An energy analysis of IEEE 802.15.6 scheduled access modes. In Proceedings of the 2010 IEEE Globecom Workshops, Miami, FL, USA, 6–10 October 2012; pp. 1270–1275. [Google Scholar]
- Movassaghi, S.; Abolhasan, M.; Lipman, J. A Review of Routing Protocols in Wireless Body Area Networks. J. Netw. 2013, 8, 559–575. [Google Scholar] [CrossRef]
- Bangash, J.I.; Abdullah, A.H.; Anisi, M.H.; Khan, A.W. A Survey of Routing Protocols in Wireless Body Sensor Networks. Sensors 2014, 14, 1322–1357. [Google Scholar] [CrossRef] [PubMed]
- Ning, Z.; Liu, L.; Xia, F.; Jedari, B.; Lee, I.; Zhang, W. CAIS: A copy adjustable incentive scheme in community-based socially-aware networking. IEEE Trans. Veh. Technol. 2017, 66, 3406–3419. [Google Scholar] [CrossRef]
- Ning, Z.; Xia, F.; Ullah, N.; Kong, X.; Hu, X. Vehicular social networks: Enabling smart mobility. IEEE Commun. Mag. 2017, 55, 49–55. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Karaboga, D.; Akay, B. A comparative study of Artificial Bee Colony algorithm. Appl. Math. Comput. 2009, 214, 108–132. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. On the performance of artificial bee colony (ABC) algorithm. Appl. Soft Comput. 2008, 8, 687–697. [Google Scholar] [CrossRef]
- Watteyne, T.; Auge-Blum, S.; Dohler, M.; Barthel, D. Anybody: A self-organization protocol for body area networks. In Proceedings of the ICST 2nd international conference on Body area networks, Florence, Italy, 11–13 June 2007. [Google Scholar]
- Culpepper, B.J.; Dung, L.; Moh, M. Design and analysis of hybrid indirect transmissions (HIT) for data gathering in wireless micro sensor networks. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2004, 8, 61–83. [Google Scholar] [CrossRef]
- Moh, M.; Culpepper, B.; Dung, L.; Moh, T.-S.; Hamada, T.; Su, C.F. On data gathering protocols for in-body biomedical sensor networks. In Proceedings of the IEEE Global Telecommunications Conference, St. Louis, MO, USA, 28 November–2 December 2005. [Google Scholar]
- Braem, B.; Latre, B.; Moerman, I.; Blondia, C.; Demeester, P. The wireless autonomous spanning tree protocol for multihop wireless body area networks. In Proceedings of the Third Annual International Conference on Mobile and Ubiquitous Systems: Networking Services, San Jose, CA, USA, 17–21 July 2006; pp. 1–8. [Google Scholar]
- Braem, B.; Latre, B.; Blondia, C.; Moerman, I.; Demeester, P. Improving reliability in multi-hop body sensor networks. In Proceedings of the 2008 Second International Conference on Sensor Technologies and Applications, Cap Esterel, France, 25–31 August 2008; pp. 342–347. [Google Scholar]
- Latre, B.; Braem, B.; Moerman, I.; Blondia, C.; Reusens, E.; Joseph, W.; Demeester, P. A low-delay protocol for multihop wireless body area networks. In Proceedings of the Fourth Annual International Conference on Mobile and Ubiquitous Systems: Networking Services, Philadelphia, PA, USA, 6–10 August 2007; pp. 1–8. [Google Scholar]
- Braem, B.; Latr, B.; Moerman, I.; Blondia, C.; Reusens, E.; Joseph, W. The Need for Cooperation and Relaying in Short-Range High Path Loss Sensor Networks. In Proceedings of the International Conference on Sensor Technologies and Applications, Valencia, Spain, 14–20 October 2007; pp. 566–571. [Google Scholar]
- Joseph, W.; Braem, B.; Reusens, E. Design of Energy Efficient Topologies for Wireless On-Body Channel. In Proceedings of the Seventeenth Wireless Conference-Sustainable Wireless Technologies, Vienna, Austria, 27–29 April 2011; pp. 1–7. [Google Scholar]
- Ferrand, P.; Maman, M.; Goursaud, C. Performance evaluation of direct and cooperative transmissions in body area networks. Ann. Telecommun. 2011, 66, 213–228. [Google Scholar] [CrossRef]
- Maskooki, A.; Soh, C.B.; Gunawan, E.; Low, K.S. Opportunistic routing for body area network. In Proceedings of the IEEE Consumer Communications and Networking Conference (CCNC), Las Vegas, NV, USA, 8–11 January 2011; pp. 237–241. [Google Scholar]
- Liang, X.; Li, X.; Shen, Q.; Lu, R.; Lin, X.; Shen, X.; Zhang, W. Exploiting Prediction to Enable Secure and Reliable Routing in Wireless Body Area Networks. In Proceedings of the Thirty-First IEEE International Conference on Computer Communications (INFOCOM), Orlando, FL, USA, 25–30 March 2012; pp. 388–396. [Google Scholar]
- Quwaider, M.; Biswas, S. Probabilistic routing in on-body sensor networks with postural disconnections. In Proceedings of the Seventh ACM International Symposium on Mobility Management and Wireless Access, Tenerife, Canary Islands, Spain, 26–27 October 2009; pp. 149–158. [Google Scholar]
- Quwaider, M.; Biswas, S. On-body packet routing algorithms for body sensor networks. In Proceedings of the First International Conference on Networks and Communications (NETCOM ’09), Washington, DC, USA, 27–29 December 2009; pp. 171–177. [Google Scholar]
- Djenouri, D.; Balasingham, I. New QoS and geographical routing in wireless biomedical sensor networks. In Proceedings of the Sixth International Conference on Broadband Communications, Networks, and Systems (BROADNETS), Madrid, Spain, 14–16 September 2009; pp. 1–8. [Google Scholar]
- Razzaque, M.A.; Hong, C.S.; Lee, S. Data-centric multiobjective QoS-aware routing protocol for body sensor networks. Sensors 2011, 11, 917–937. [Google Scholar] [CrossRef] [PubMed]
- Zuhra, F.; Bakar, K.; Ahmed, A.; Tunio, M. Routing protocols in wireless body sensor networks: A comprehensive survey. J. Netw. Comput. Appl. 2017, 99, 73–97. [Google Scholar] [CrossRef]
- Takahashi, D.; Xiao, Y.; Hu, F.; Chen, J.; Sun, Y. Temperature aware routing for telemedicine applications in embedded biomedical sensor networks. EURASIP J. Wirel. Commun. Netw. 2008, 26. [Google Scholar] [CrossRef]
- Shah, R.; Yarvis, M. TARA: Thermal-aware routing algorithm for implanted sensor networks. In International Conference on Distributed Computing in Sensor Systems; Springer: Berlin/Heidelberg, Germany, 2005; pp. 206–217. [Google Scholar]
- Bag, A.; Bassiouni, M.A. Energy efficient thermal aware routing algorithms for embedded biomedical sensor networks. In Proceedings of the IEEE International Conference on Mobile Adhoc and Sensor Systems (MASS), Vancouver, BC, Canada, 9–12 October 2006; pp. 604–609. [Google Scholar]
- Mitra, R.; Sharma, S. Proactive data routing using controlled mobility of a mobile sink in Wireless Sensor Networks. Comput. Electr. Eng. 2018, 70, 21–36. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Holland, J.H. Genetic algorithms and machine learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Dorigo, M.; Blum, C. Ant colony optimization theory: A survey. Theor. Comput. Sci. 2005, 344, 243–278. [Google Scholar] [CrossRef]

| Routing Protocol | Routing Mechanism | Advantage | Disadvantage | Energy Consumption |
|---|---|---|---|---|
| Star topology | Single Hop | Low delay | High energy consumption | High |
| AnyBody [17] | Cluster-Based Multi Hop | Reliable, low load | More complex | Medium |
| HIT [18,19] | Cluster-Based Multi Hop | Reliable, low load | More complex | Medium |
| WASP [20] | Cross-Layer Multi Hop | Reliable, low load | Large network delay | Medium |
| CICADA [21,22] | Cross-Layer Multi Hop | Reliable, low load | Large network delay | Medium |
| [23,24,25] | Collaborative | Low packet loss rate and low network delay | Unable to adapt to frequent network topology changes | Low |
| Parameter | Value |
|---|---|
| Simulation area: | 100 m × 100 m |
| Energy model: | Generic radio energy model |
| Attenuation model: | Two ray |
| Signal transmission range: | 10 m |
| Signal interference range: | 20 m |
| Packet size: | 512 Byte |
| Output queue type: | First-In First-Out (FIFO) |
| Channel capacity: | 1 Mbit/s |
| Cache capacity: | 50 packets |
| No. | Path | η | C | E | Fitness |
|---|---|---|---|---|---|
| 1 | v0, v6, v19, v35, v53, v67, v88, v100, v112, v133, v140, v150 | 0.57 | 0.63 | 26 | 46.97 |
| 2 | v0, v5, v28, v37, v60, v75, v84, v100, v118, v132, v138, v150 | 0.49 | 0.56 | 29 | 45.26 |
| 3 | v0, v13, v28, v35, v49, v71, v81, v97, v107, v123, v136, v150 | 0.67 | 0.48 | 31 | 57.43 |
| 4 | v0, v10, v23, v43, v48, v74, v85, v93, v114, v134, v139, v150 | 0.68 | 0.45 | 22 | 58.42 |
| 5 | v0, v7, v27, v41, v56, v73, v90, v93, v109, v131, v149, v150 | 0.49 | 0.44 | 19 | 49.13 |
| No. | Path | η | C | E | Fitness |
|---|---|---|---|---|---|
| 1 | v0, v6, v19, v35, v53, v67, v88, v100, v112, v133, v140, v150 | 0.63 | 0.61 | 23 | 50.19 |
| 2 | v0, v5, v28, v37, v60, v75, v84, v100, v118, v132, v138, v150 | 0.49 | 0.56 | 29 | 45.26 |
| 3 | v0, v13, v28, v35, v49, v71, v81, v97, v107, v123, v136, v150 | 0.67 | 0.48 | 31 | 57.43 |
| 4 | v0, v10, v23, v43, v48, v74, v85, v93, v114, v134, v139, v150 | 0.69 | 0.43 | 20 | 59.76 |
| 5 | v0, v7, v27, v41, v56, v73, v90, v93, v109, v131, v149, v150 | 0.49 | 0.44 | 19 | 49.13 |
| No. | Path | η | C | E | Fitness |
|---|---|---|---|---|---|
| 1 | v0, v6, v19, v35, v53, v67, v88, v100, v112, v133, v140, v150 | 0.63 | 0.61 | 23 | 50.19 |
| 2 | v0, v5, v28, v37, v60, v75, v84, v100, v118, v132, v138, v150 | 0.51 | 0.56 | 29 | 46.26 |
| 3 | v0, v13, v28, v35, v49, v71, v81, v97, v107, v123, v136, v150 | 0.66 | 0.45 | 23 | 57.52 |
| 4 | v0, v10, v23, v43, v48, v74, v85, v93, v114, v134, v139, v150 | 0.69 | 0.43 | 20 | 59.76 |
| 5 | v0, v7, v27, v41, v56, v73, v90, v93, v109, v131, v149, v150 | 0.49 | 0.44 | 19 | 49.13 |
| No. | Path | η | C | E | Fitness |
|---|---|---|---|---|---|
| 1 | v0, v6, v19, v35, v53, v67, v88, v100, v112, v133, v140, v150 | 0.69 | 0.51 | 21 | 56.21 |
| 2 | v0, v5, v28, v37, v60, v75, v84, v100, v118, v132, v138, v150 | 0.51 | 0.42 | 27 | 52.01 |
| 3 | v0, v13, v28, v35, v49, v71, v81, v97, v107, v123, v136, v150 | 0.75 | 0.31 | 17 | 71.46 |
| 4 | v0, v10, v23, v43, v48, v74, v85, v93, v114, v134, v139, v150 | 0.73 | 0.33 | 18 | 68.60 |
| 5 | v0, v7, v27, v41, v56, v73, v90, v93, v109, v131, v149, v150 | 0.54 | 0.39 | 17 | 54.34 |
| Run Times | OEABC | Genetic Algorithm | Ant Colony Algorithm |
|---|---|---|---|
| 50 | 16.00% | 14.00% | 18.00% |
| 100 | 15.00% | 16.00% | 11.00% |
| 150 | 16.67% | 13.33% | 17.33% |
| Average | 15.89% | 14.44% | 15.44% |
| Population Size | OEABC | Genetic Algorithm | Ant Colony Algorithm |
|---|---|---|---|
| 20 | 0.81 | 0.76 | 0.83 |
| 30 | 0.89 | 0.92 | 0.89 |
| 40 | 1.17 | 1.08 | 1.01 |
| Average | 0.96 | 0.92 | 0.91 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, J.; Peng, Y.; Shen, D.; Yan, X.; Deng, Q. An Artificial Bee Colony-Based Green Routing Mechanism in WBANs for Sensor-Based E-Healthcare Systems. Sensors 2018, 18, 3268. https://doi.org/10.3390/s18103268
Yan J, Peng Y, Shen D, Yan X, Deng Q. An Artificial Bee Colony-Based Green Routing Mechanism in WBANs for Sensor-Based E-Healthcare Systems. Sensors. 2018; 18(10):3268. https://doi.org/10.3390/s18103268
Chicago/Turabian StyleYan, Jian, Yuhuai Peng, Dawei Shen, Xinxin Yan, and Qingxu Deng. 2018. "An Artificial Bee Colony-Based Green Routing Mechanism in WBANs for Sensor-Based E-Healthcare Systems" Sensors 18, no. 10: 3268. https://doi.org/10.3390/s18103268
APA StyleYan, J., Peng, Y., Shen, D., Yan, X., & Deng, Q. (2018). An Artificial Bee Colony-Based Green Routing Mechanism in WBANs for Sensor-Based E-Healthcare Systems. Sensors, 18(10), 3268. https://doi.org/10.3390/s18103268





