High Precision Position Measurement Method for Laguerre-Gaussian Beams Using a Quadrant Detector
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theoretical Analyses of L-G Beams and Quadrant Detector
2.1.1. Intensity Distribution of L-G Beams
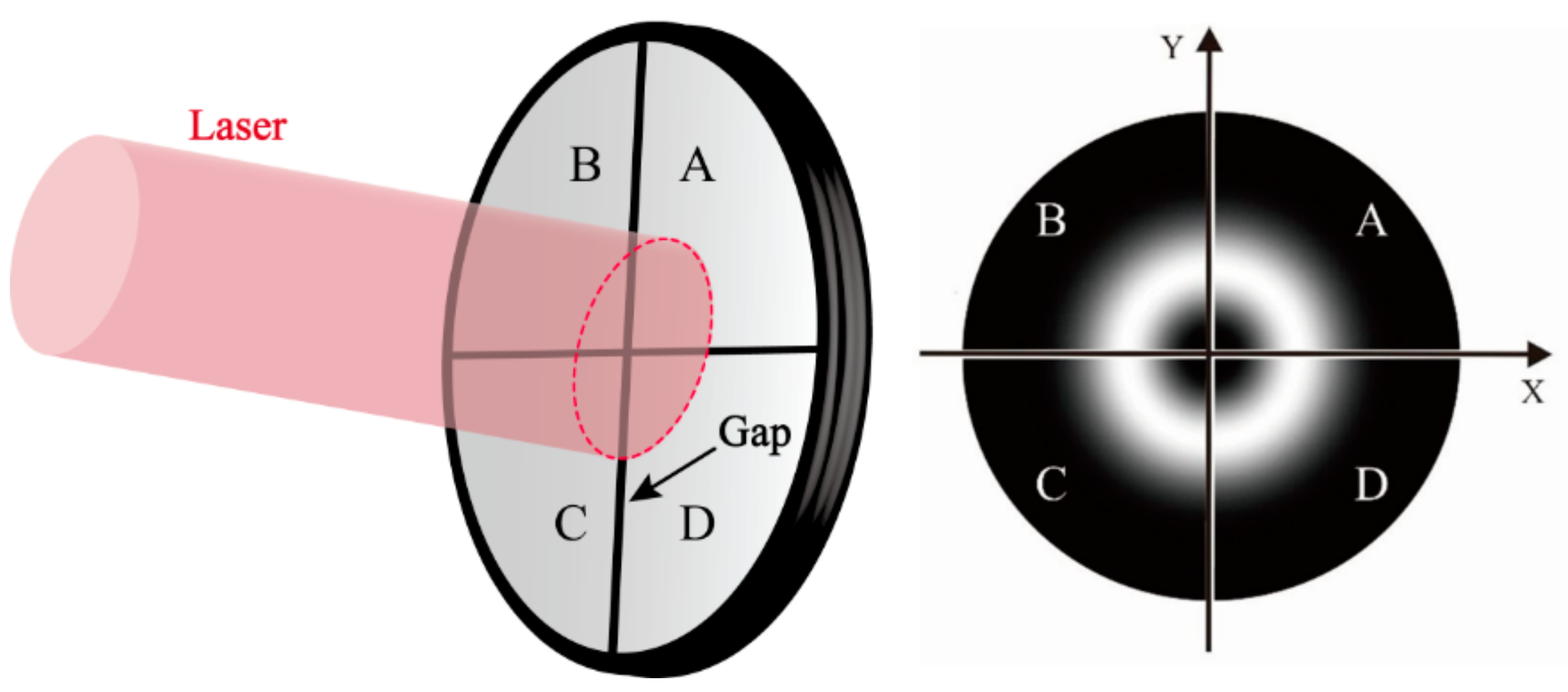
2.1.2. Position Measurement Principle of the QD
2.2. Improved New Estimation Method
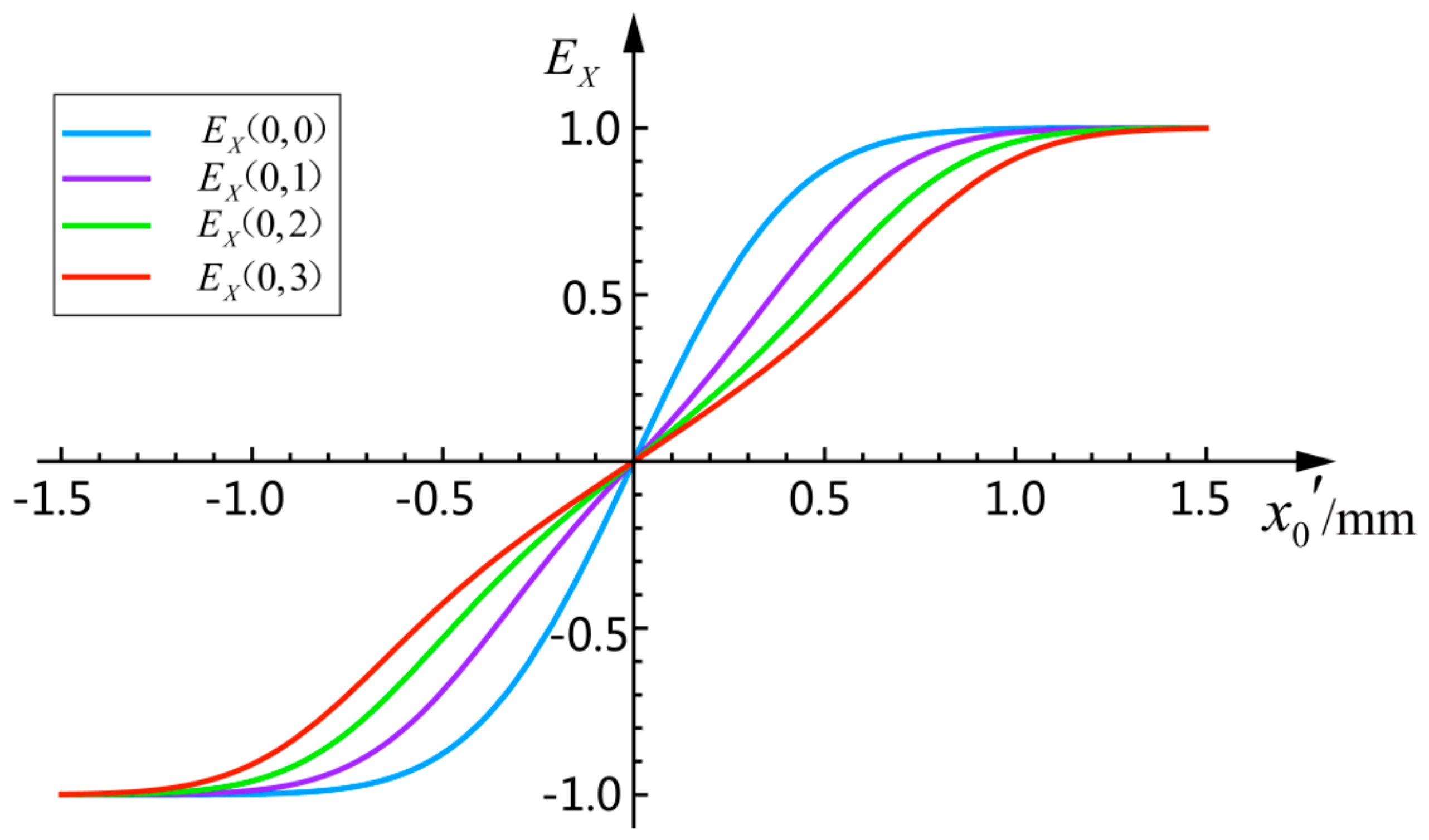
2.2.1. Infinite Integral Method
2.2.2. Improved New Estimation Method
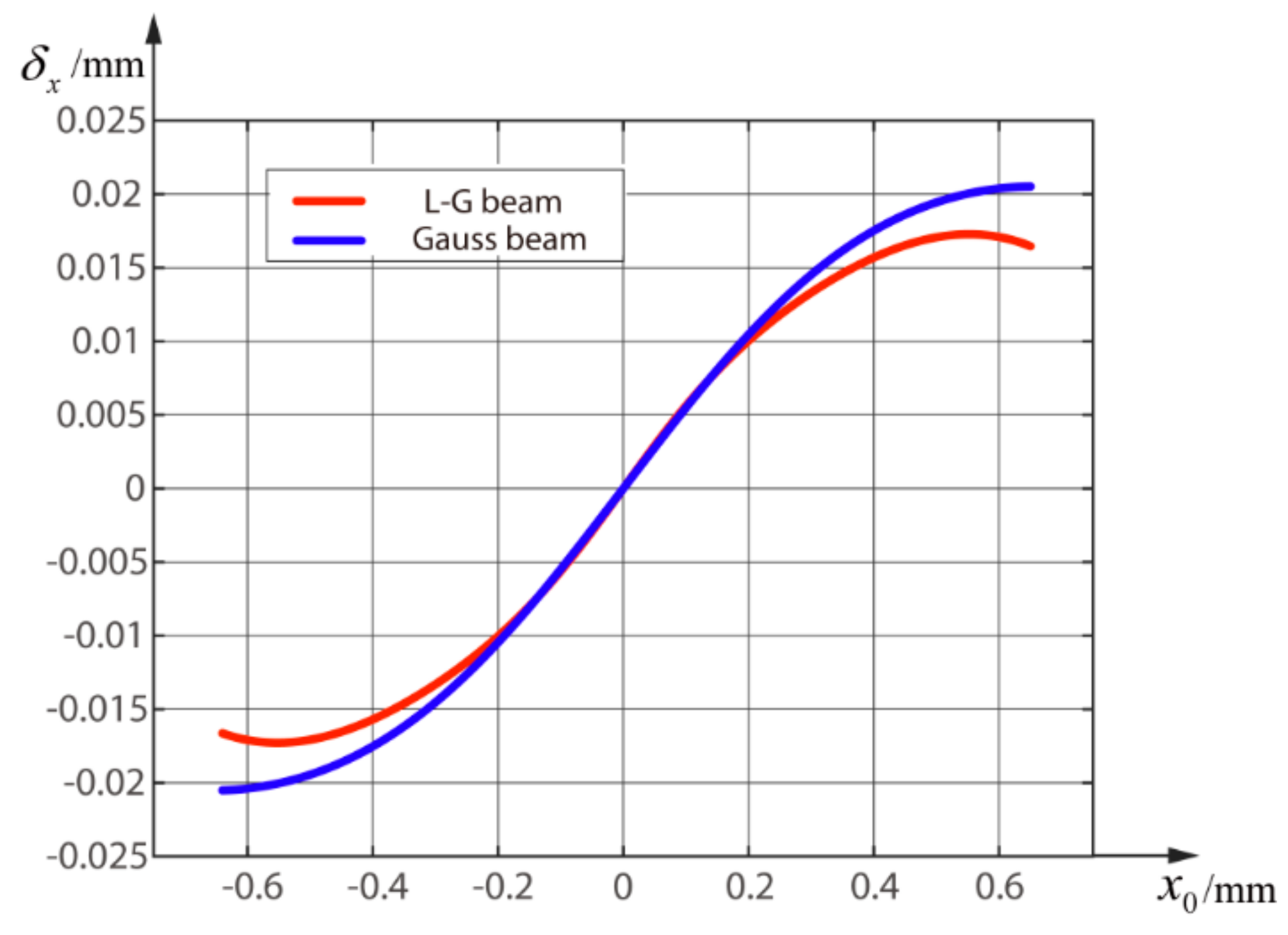
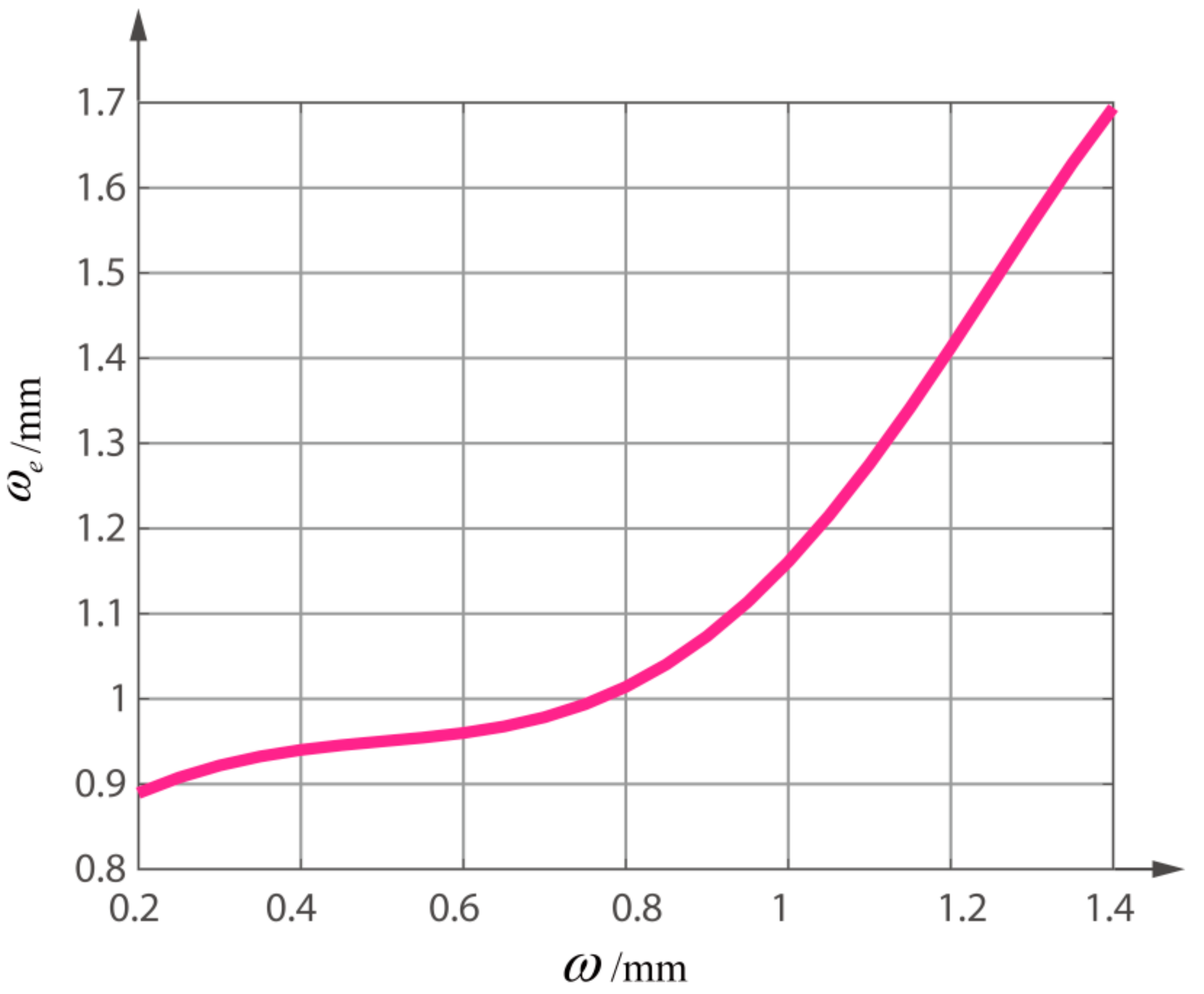
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, R.; Wang, H. Propagation of Laguerre–Gaussian beams in cubic-quantic nonlinear media by variational approach. Opt. Laser Technol. 2010, 42, 1318–1322. [Google Scholar] [CrossRef]
- Zhu, J.; Li, X.; Tang, H.; Zhu, K. Propagation of multi-cosine-Laguerre Gaussian correlated Schell-model beams in free space and atmospheric turbulence. Opt. Express 2017, 25, 20071–20086. [Google Scholar] [CrossRef] [PubMed]
- Saad, F.; Mostafa, E.; Halba, E.; Belafhal, A. Diffraction by a radial phase modulated spiral zone plate of abruptly autofocusing beams generated with multiple Bessel-like beams. Opt. Laser Technol. 2018, 107, 366–371. [Google Scholar] [CrossRef]
- Picón, A.; Benseny, A.; Mompart, J.; de Aldana, J.R.V.; Plaja, L.; Calvo, G.F.; Roso, L. Transferring orbital and spin angular momenta of light to atoms. New J. Phys. 2010, 12, 083053. [Google Scholar] [CrossRef] [Green Version]
- Willner, A.E.; Wang, J.; Huang, H. A Different Angle on Light Communications. Science 2012, 337, 655–656. [Google Scholar] [CrossRef] [PubMed]
- Pilát, Z.; Jonáš, A.; Ježek, J.; Zemánek, P. Effects of Infrared Optical Trapping on Saccharomyces cerevisiae in a Microfluidic System. Sensors 2017, 17, 2640. [Google Scholar] [CrossRef] [PubMed]
- Leach, J.; Sinclair, G.; Jordan, P.; Courtial, J.; Padgett, M.J.; Cooper, J.; Laczik, Z.J. 3D manipulation of particles into crystal structures using holographic optical tweezers. Opt. Express 2004, 12, 220–226. [Google Scholar] [CrossRef] [PubMed]
- Morris, J.E.; Carruthers, A.E.; Mazilu, M.; Reece, P.J.; Cizmar, T.; Fischer, P.; Dholakia, K. Optical micromanipulation using supercontinuum Laguerre-Gaussian and Gaussian beams. Opt. Express 2008, 16, 10117–10129. [Google Scholar] [CrossRef] [PubMed]
- Sinclair, G.; Jordan, P.; Courtial, J.; Padgett, M.; Cooper, J.; Laczik, Z.J. Assembly of 3-dimensional structures using programmable holographic optical tweezers. Opt. Express 2004, 12, 5475–5480. [Google Scholar] [CrossRef] [PubMed]
- Grier, D. A revolution in optical manipulation. Nature 2003, 424, 810–816. [Google Scholar] [CrossRef] [PubMed]
- Nugrowati, A.M.; Stam, W.G.; Woerdman, J.P. Position Sensitive Detection Techniques for Manufacturing Accuracy Control. Opt. Express 2012, 20, 27429–27441. [Google Scholar] [CrossRef] [PubMed]
- Manojlović, L.M. Quadrant photodetector sensitivity. Appl. Opt. 2011, 50, 3461–3469. [Google Scholar] [CrossRef] [PubMed]
- Dang, L.; Zhou, Z.; Tang, S. The characteristic analysis and optimization of quadrant detector signal. In Proceedings of the IEEE International Conference on Intelligent Computing and Intelligent Systems, Shanghai, China, 28 December 2009. [Google Scholar]
- Hermosa, N.; Aiello, A.; Woerdman, J.P. Quadrant detector calibration for vortex beams. Opt. Lett. 2011, 36, 409–411. [Google Scholar] [CrossRef] [PubMed]
- Garbin, V.; Volpe, G.; Ferrari, E.; Versluis, M.; Cojoc, D.; Petrov, D. Mie scattering distinguishes the topological charge of an optical vortex: A homage to Gustav Mie. New J. Phys. 2009, 11, 013046. [Google Scholar] [CrossRef]
- Cui, S.; Soh, Y.C. Linearity Indices and Linearity Improvement of 2-D Tetralateral Position-Sensitive Detector. IEEE Trans. Electron Devices 2010, 57, 2310–2316. [Google Scholar] [CrossRef]
- Cui, S.; Soh, Y.C. Analysis and improvement of Laguerre-Gaussian beam position estimation using quadrant detectors. Opt. Lett. 2011, 36, 1692–1694. [Google Scholar] [CrossRef] [PubMed]
- Jing, X.; Cheng, H.; Xu, C.; Feng, Y. Method to measure the position offset of multiple light spots in a distributed aperture laser angle measurement system. Appl. Opt. 2017, 56, 1740–1747. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Chen, Y.; Gao, S.; Li, Y.; Wu, Z. Improved measurement accuracy of spot position on a n In GaAs quadrant detector. Appl. Opt. 2015, 54, 8049–8054. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Zhang, R.; Xie, G.; Ren, Y.; Zhao, Z.; Wang, Z.; Liu, C.; Song, H.; Pang, K.; Bock, R.; et al. Experimental demonstration of beaconless beam displacement tracking for an orbital angular momentum multiplexed free-space optical link. Opt. Lett. 2018, 43, 2392–2395. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Zhang, R.; Zhao, Z.; Xie, G.; Liao, P.; Pang, K.; Song, H.; Liu, C.; Ren, Y.; Labroille, G.; et al. High-Capacity Free-Space Optical Communications Between a Ground Transmitter and a Ground Receiver via a UAV Using Multipl exing of Multiple Orbital Angular-Momentum Beams. Sci. Rep. 2017, 7, 17427. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.; Zhai, Y.; Wang, X.; Guo, Y.; Du, Y.; Yang, G. A novel method to improve detecting sensitivity of quadrant detector. Optik 2014, 125, 3519–3523. [Google Scholar] [CrossRef]
- Li, D.; Liu, S. Research on four-quadrant detector and its precise detection. Int. J. Digit. Content Technol. Appl. 2011, 5, 138–143. [Google Scholar]
- Chen, M.; Yang, Y.; Jia, X.; Gao, H. Investigation of positioning algorithm and method for increasing the linear measurement range for four-quadrant detector. Optik 2013, 124, 6806–6809. [Google Scholar] [CrossRef]




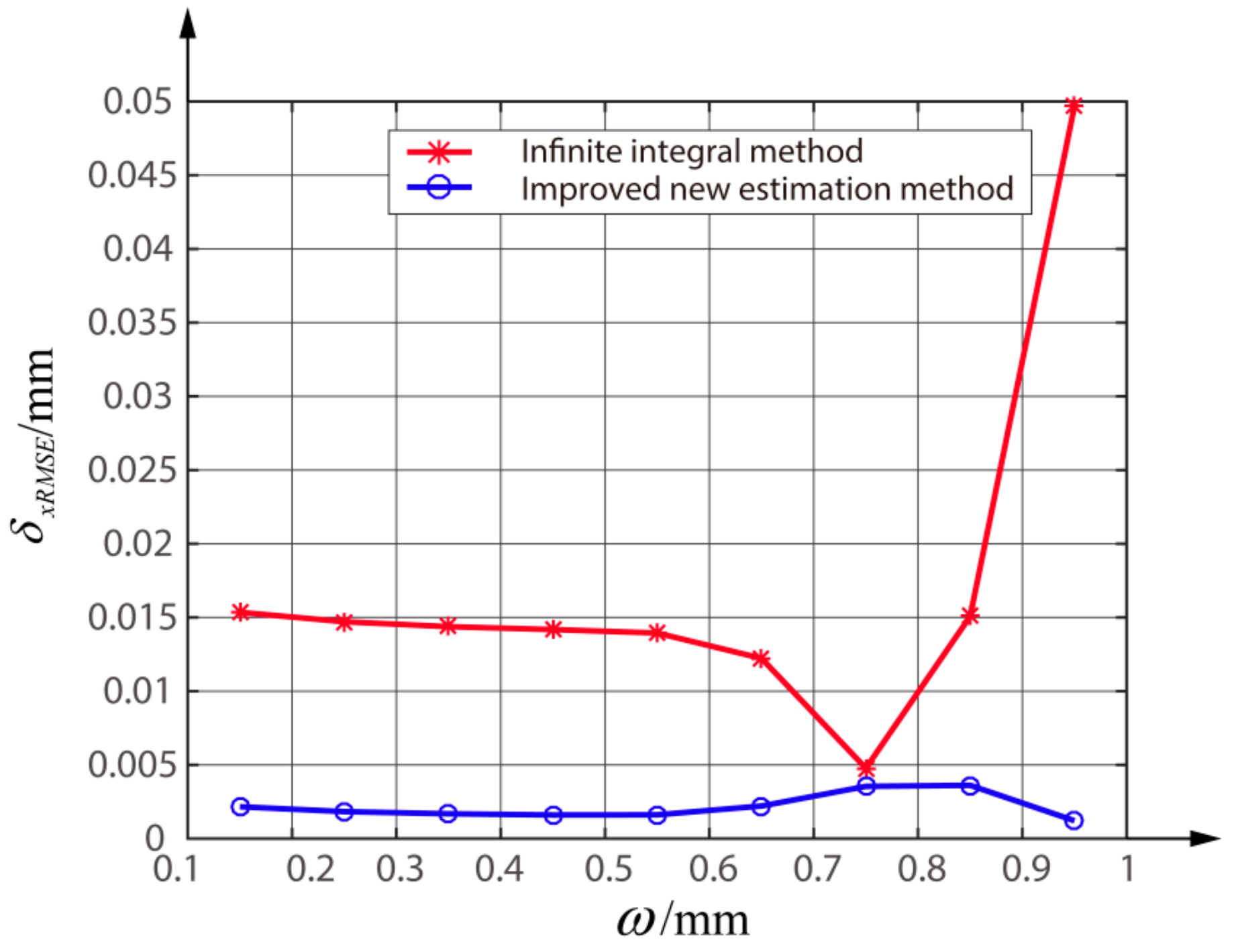
| 0.15 | 0.9057 | 0.0225 | 0.0047 | 79.1% |
| 0.25 | 0.9216 | 0.0227 | 0.0039 | 82.8% |
| 0.35 | 0.9359 | 0.0228 | 0.0036 | 84.2% |
| 0.45 | 0.9463 | 0.0228 | 0.0035 | 84.6% |
| 0.55 | 0.9556 | 0.0223 | 0.0037 | 83.4% |
| 0.65 | 0.9696 | 0.0173 | 0.0057 | 67.1% |
| 0.75 | 0.9957 | 0.0095 | 0.0076 | 25.0% |
| 0.85 | 1.0414 | 0.0419 | 0.0097 | 76.8% |
| 0.95 | 1.1124 | 0.0960 | 0.0025 | 97.4% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Wu, J.; Chen, Y.; Wang, J.; Gao, S.; Wu, Z. High Precision Position Measurement Method for Laguerre-Gaussian Beams Using a Quadrant Detector. Sensors 2018, 18, 4007. https://doi.org/10.3390/s18114007
Li Q, Wu J, Chen Y, Wang J, Gao S, Wu Z. High Precision Position Measurement Method for Laguerre-Gaussian Beams Using a Quadrant Detector. Sensors. 2018; 18(11):4007. https://doi.org/10.3390/s18114007
Chicago/Turabian StyleLi, Qian, Jiabin Wu, Yunshan Chen, Jingyuan Wang, Shijie Gao, and Zhiyong Wu. 2018. "High Precision Position Measurement Method for Laguerre-Gaussian Beams Using a Quadrant Detector" Sensors 18, no. 11: 4007. https://doi.org/10.3390/s18114007






