Multiband Envelope Spectra Extraction for Fault Diagnosis of Rolling Element Bearings
Abstract
:1. Introduction
2. Multiband Envelope Spectra Extraction
2.1. Frequency Band Segmentation
2.2. Narrow Band Selection
2.3. Blind Source Separation
2.4. Summary of the Proposed Method
3. Simulation
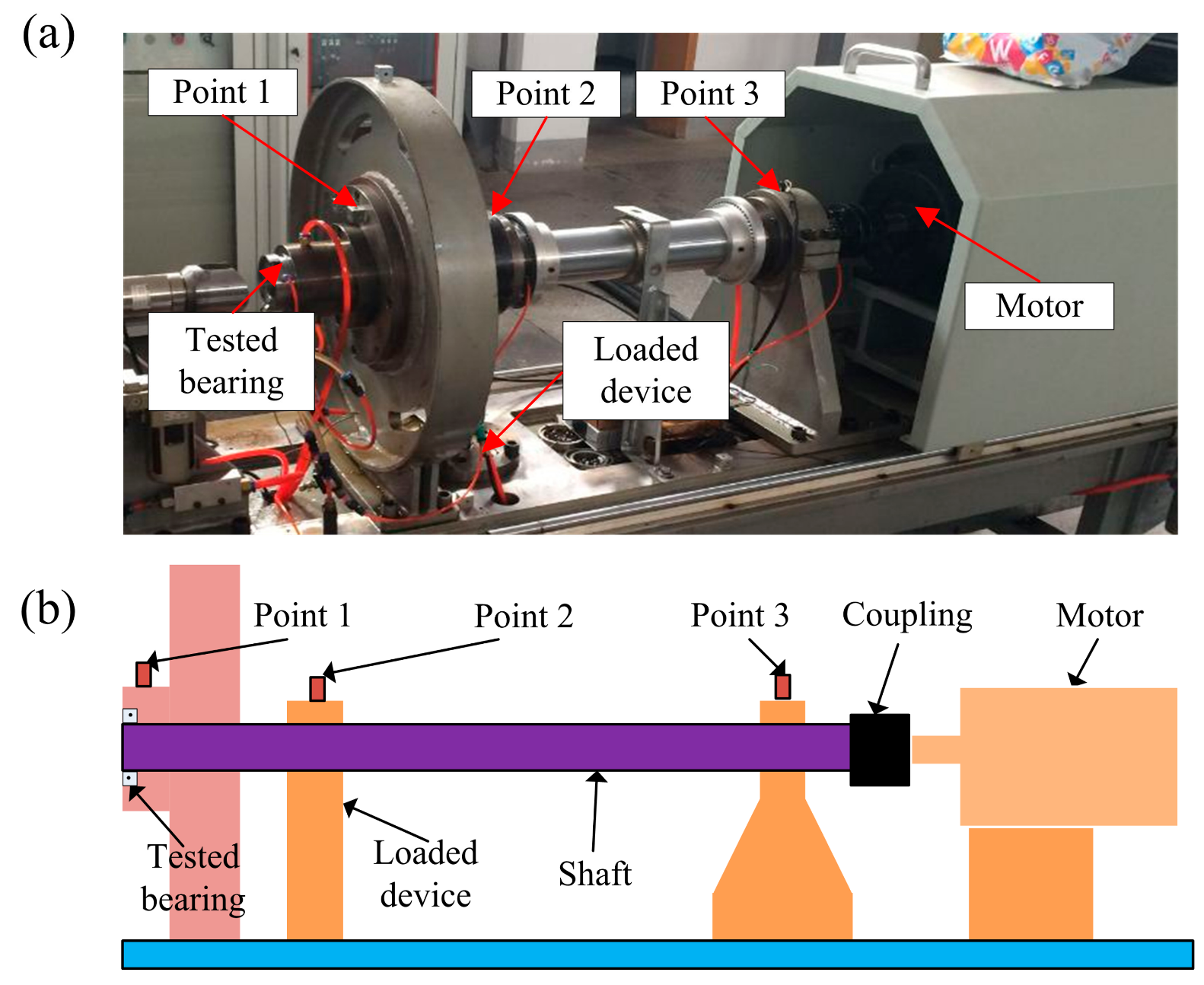
4. Experiment
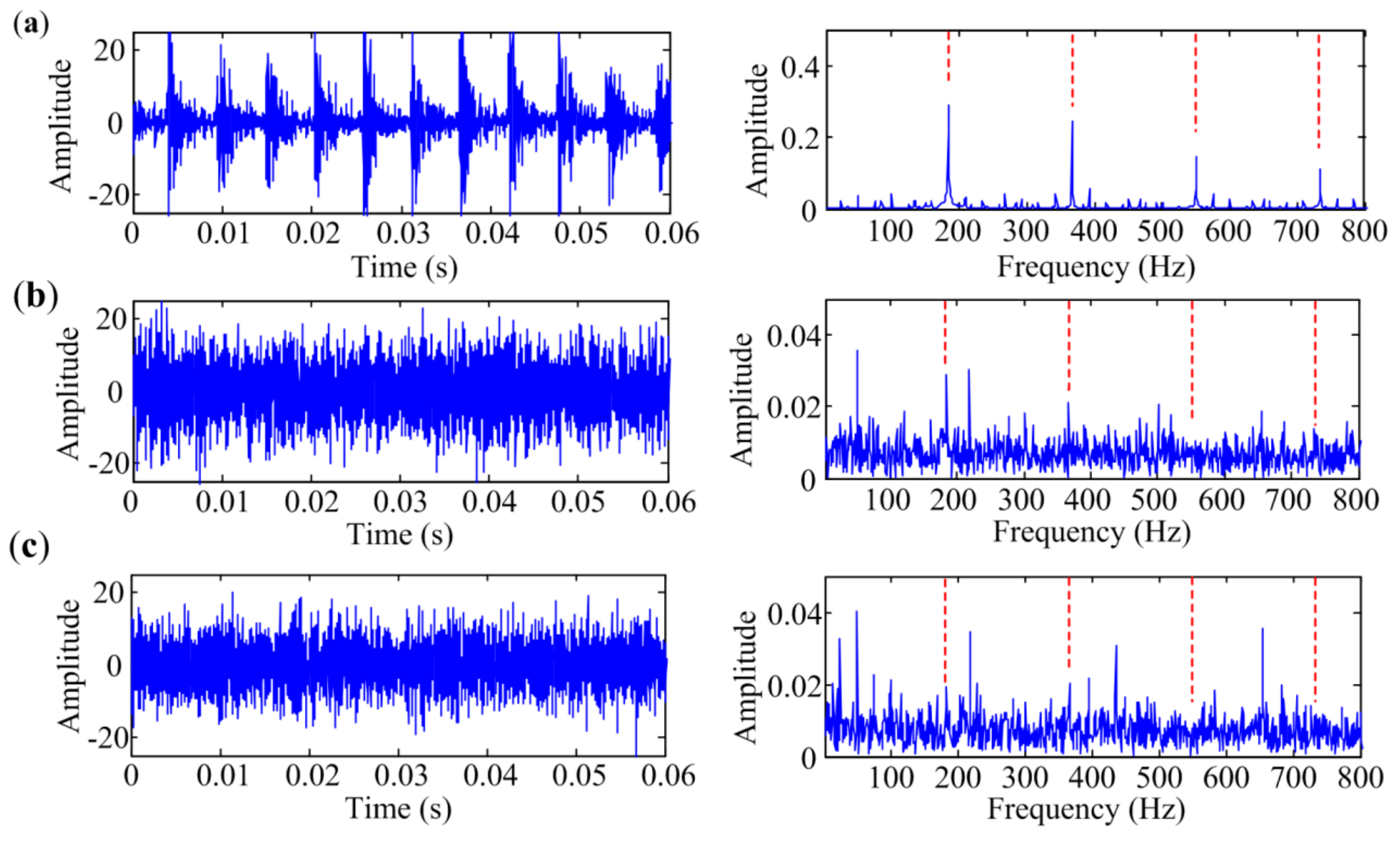
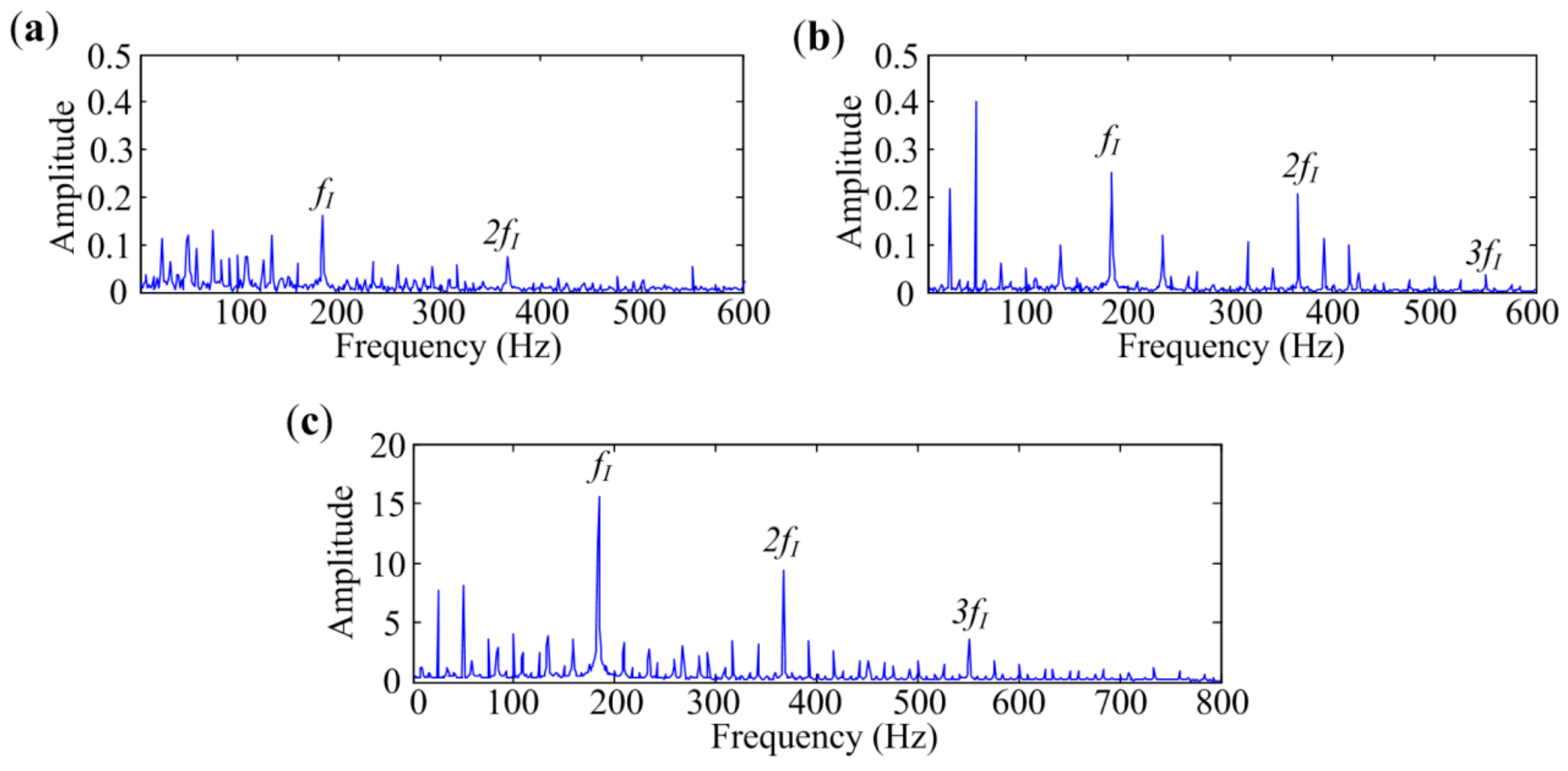
4.1. Bearing Inner-Race Defect Identification
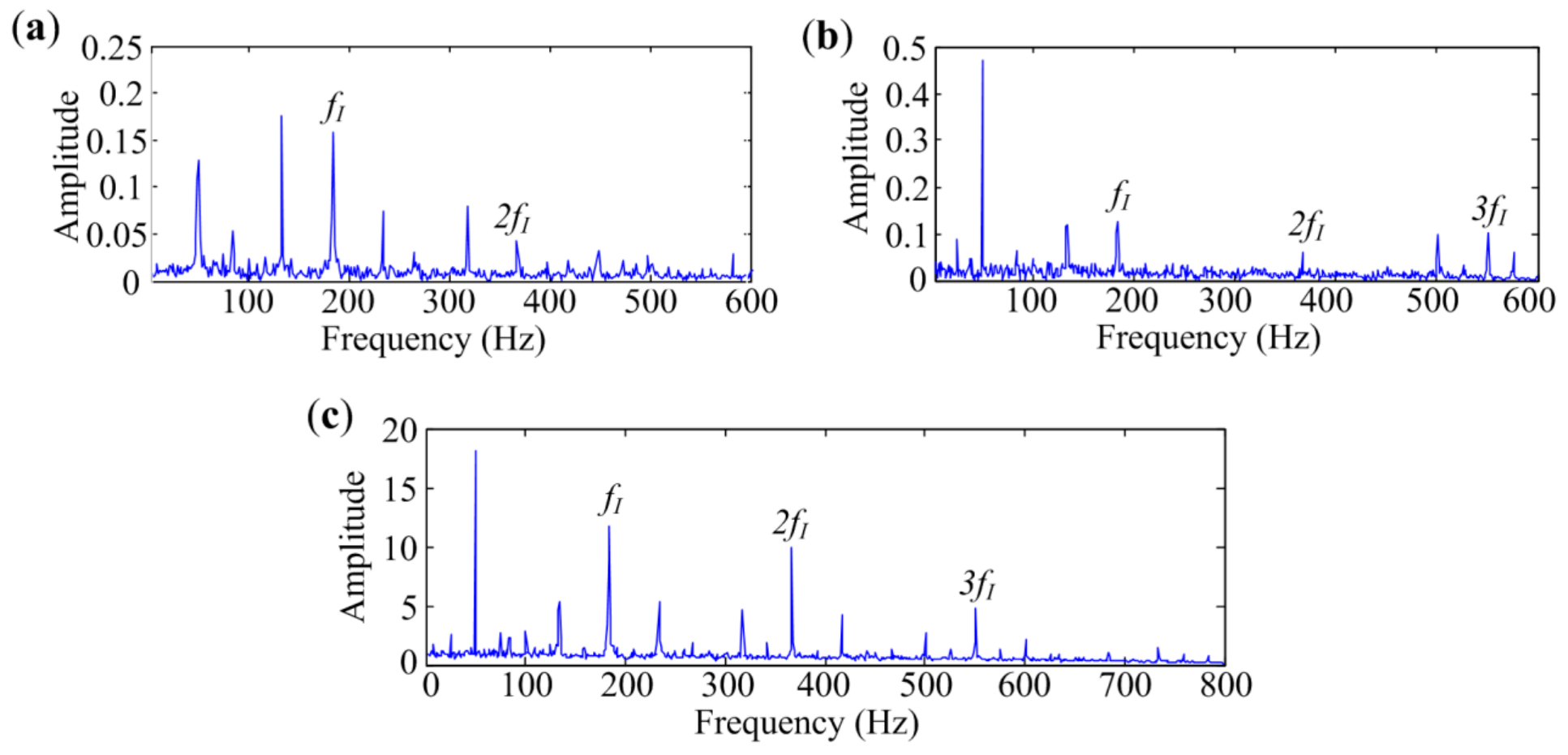
4.2. Bearing Outer-Race Defect Identification
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, C.; Wang, G.; Xie, Q.; Zhang, Y. Vibration sensor-based bearing fault diagnosis using ellipsoid-artmap and differential evolution algorithms. Sensors 2014, 14, 10598–10618. [Google Scholar] [CrossRef] [PubMed]
- Rai, A.; Upadhyay, S.H. A review on signal processing techniques utilized in the fault diagnosis of rolling element bearings. Tribol. Int. 2016, 96, 289–306. [Google Scholar] [CrossRef]
- Zhou, H.; Shi, T.; Liao, G.; Xuan, J.; Duan, J. Weighted kernel entropy component analysis for fault diagnosis of rolling bearings. Sensors 2017, 17, 625. [Google Scholar] [CrossRef] [PubMed]
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Nikolaou, N.G.; Antoniadis, I.A. Demodulation of vibration signals generated by defects in rolling element bearings using complex shifted morlet wavelets. Mech. Syst. Signal Process. 2002, 16, 677–694. [Google Scholar] [CrossRef]
- Feldman, M. Hilbert transform in vibration analysis. Mech. Syst. Signal Process. 2011, 25, 735–802. [Google Scholar] [CrossRef]
- Rubini, R.; Meneghetti, U. Application of the envelope and wavelet transform analyses for the diagnosis of incipient faults in ball bearings. Mech. Syst. Signal Process. 2001, 15, 287–302. [Google Scholar] [CrossRef]
- Tse, P.W.; Yang, W.X.; Tam, H.Y. Machine fault diagnosis through an effective exact wavelet analysis. J. Sound Vib. 2004, 277, 1005–1024. [Google Scholar] [CrossRef]
- Su, W.; Wang, F.; Zhu, H.; Zhang, Z.; Guo, Z. Rolling element bearing faults diagnosis based on optimal morlet wavelet filter and autocorrelation enhancement. Mech. Syst. Signal Process. 2010, 24, 1458–1472. [Google Scholar] [CrossRef]
- Guo, W.; Tse, P.W.; Djordjevich, A. Faulty bearing signal recovery from large noise using a hybrid method based on spectral kurtosis and ensemble empirical mode decomposition. Measurement 2012, 45, 1308–1322. [Google Scholar] [CrossRef]
- Antoni, J. The spectral kurtosis: A useful tool for characterising non-stationary signals. Mech. Syst. Signal Process. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Dwyer, R.F. A technique for improving detection and estimation of signals contaminated by under ice noise. J. Acoust. Soc. Am. 1983, 74, 124–130. [Google Scholar] [CrossRef]
- Antoni, J. Fast computation of the kurtogram for the detection of transient faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, M. An adaptive SK technique and its application for fault detection of rolling element bearings. Mech. Syst. Signal Process. 2011, 25, 1750–1764. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, M. Identification of multiple transient faults based on the adaptive spectral kurtosis method. J. Sound Vib. 2012, 331, 470–486. [Google Scholar] [CrossRef]
- Li, C.; Liang, M.; Wang, T. Criterion fusion for spectral segmentation and its application to optimal demodulation of bearing vibration signals. Mech. Syst. Signal Process. 2015, 64, 132–148. [Google Scholar] [CrossRef]
- Barszcz, T.; Jabłoński, A. A novel method for the optimal band selection for vibration signal demodulation and comparison with the kurtogram. Mech. Syst. Signal Process. 2011, 25, 431–451. [Google Scholar] [CrossRef]
- Wang, D.; Tse, P.W.; Tsui, K.L. An enhanced kurtogram method for fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2013, 35, 176–199. [Google Scholar] [CrossRef]
- Antoni, J. The infogram: Entropic evidence of the signature of repetitive transients. Mech. Syst. Signal Process. 2016, 74, 73–94. [Google Scholar] [CrossRef]
- Tse, P.W.; Wang, D. The design of a new sparsogram for fast bearing fault diagnosis: Part 1 of the two related manuscripts that have a joint title as “two automatic vibration-based fault diagnostic methods using the novel sparsity measurement”. Mech. Syst. Signal Process. 2013, 40, 499–519. [Google Scholar] [CrossRef]
- Tse, P.W.; Wang, D. The automatic selection of an optimal wavelet filter and its enhancement by the new sparsogram for bearing fault detection: Part 2 of the two related manuscripts that have a joint title as “two automatic vibration-based fault diagnostic methods using the novel sparsity measurement”. Mech. Syst. Signal Process. 2013, 40, 520–544. [Google Scholar]
- Chen, X.; Zhang, B.; Feng, F.; Jiang, P. Optimal resonant band demodulation based on an improved correlated kurtosis and its application in bearing fault diagnosis. Sensors 2017, 17, 360. [Google Scholar] [CrossRef] [PubMed]
- Ming, A.B.; Qin, Z.Y.; Zhang, W.; Chu, F.L. Spectrum auto-correlation analysis and its application to fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2013, 41, 141–154. [Google Scholar] [CrossRef]
- Cong, F.; Chen, J.; Dong, G.; Zhao, F. Short-time matrix series based singular value decomposition for rolling bearing fault diagnosis. Mech. Syst. Signal Process. 2013, 34, 218–230. [Google Scholar] [CrossRef]
- Obuchowski, J.; Wyłomańska, A.; Zimroz, R. Selection of informative frequency band in local damage detection in rotating machinery. Mech. Syst. Signal Process. 2014, 48, 138–152. [Google Scholar]
- Jutten, C.; Herault, J. Blind separation of sources, part i: An adaptive algorithm based on neuromimetic architecture. Signal Process. 1991, 24, 1–10. [Google Scholar] [CrossRef]
- Karhunen, J.; Joutsensalo, J. Representation and separation of signals using nonlinear pca type learning. Neural Netw. 1994, 7, 113–127. [Google Scholar] [CrossRef]
- Comon, P. Independent component analysis, a new concept? Signal Process. 1994, 36, 287–314. [Google Scholar] [CrossRef] [Green Version]
- Bell, A.J.; Sejnowski, T.J. An information-maximization approach to blind separation and blind deconvolution. Neural Comput. 1995, 7, 1129–1159. [Google Scholar] [CrossRef] [PubMed]
- Cardoso, J.F.; Laheld, B.H. Equivariant adaptive source separation. IEEE Trans. Signal Process. 1996, 44, 3017–3030. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Oja, E. A fast fixed-point algorithm for independent component analysis. Neural Comput. 1997, 9, 1483–1492. [Google Scholar] [CrossRef]
- Hyvärinen, A. Fast and robust fixed-point algorithms for independent component analysis. IEEE Trans. Neural Netw. 1999, 10, 626–634. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Li, H.; Li, R. Applications of Wavelet to Independent Component Analysis. In Proceedings of the 6th World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; pp. 2930–2934. [Google Scholar]
- Zhao, X.; Ye, B. Selection of effective singular values using difference spectrum and its application to fault diagnosis of headstock. Mech. Syst. Signal Process. 2011, 25, 1617–1631. [Google Scholar] [CrossRef]
- Jiang, H.; Chen, J.; Dong, G.; Liu, T.; Chen, G. Study on hankel matrix-based svd and its application in rolling element bearing fault diagnosis. Mech. Syst. Signal Process. 2015, 52–53, 338–359. [Google Scholar] [CrossRef]
- Tang, M.; Wu, X.; Cong, M.; Guo, K. A method based on svd for detecting the defect using the magnetostrictive guided wave technique. Mech. Syst. Signal Process. 2016, 70–71, 601–612. [Google Scholar] [CrossRef]
- Cong, F.; Zhong, W.; Tong, S.; Tang, N.; Chen, J. Research of singular value decomposition based on slip matrix for rolling bearing fault diagnosis. J. Sound Vib. 2015, 344, 447–463. [Google Scholar] [CrossRef]
- Ho, D.; Randall, R.B. Optimisation of bearing diagnostic techniques using simulated and actual bearing fault signals. Mech. Syst. Signal Process. 2000, 14, 763–788. [Google Scholar] [CrossRef]


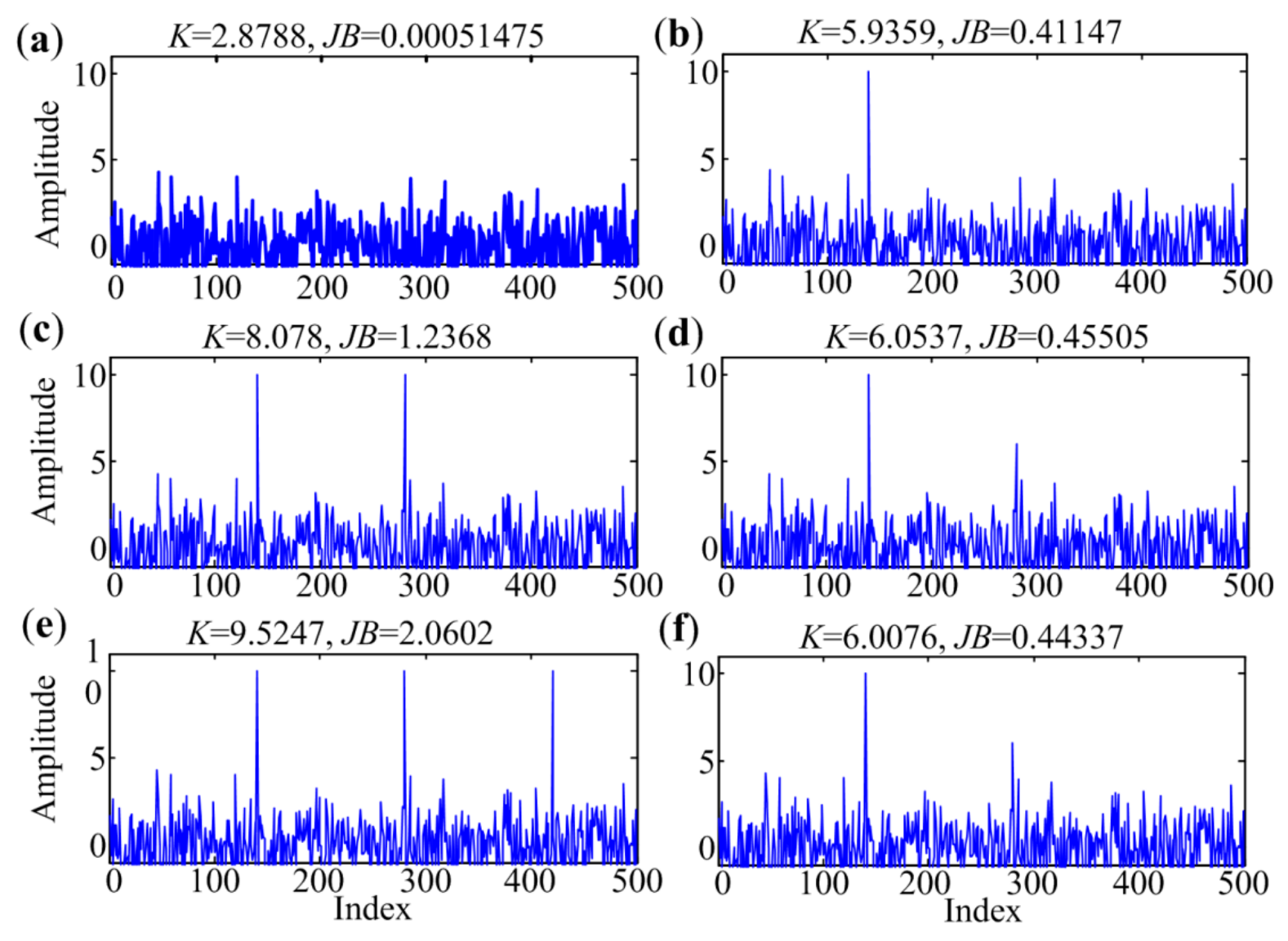


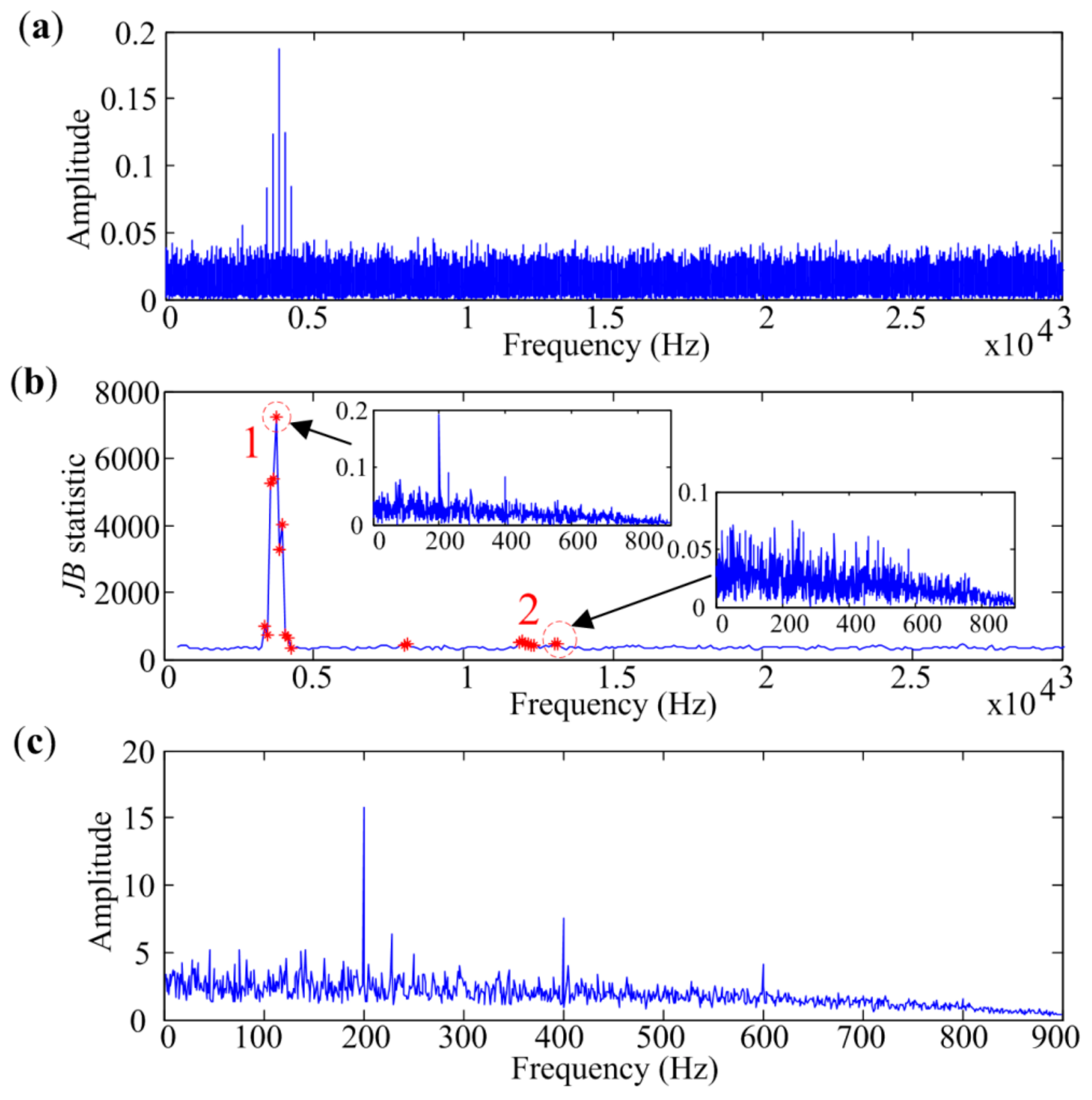
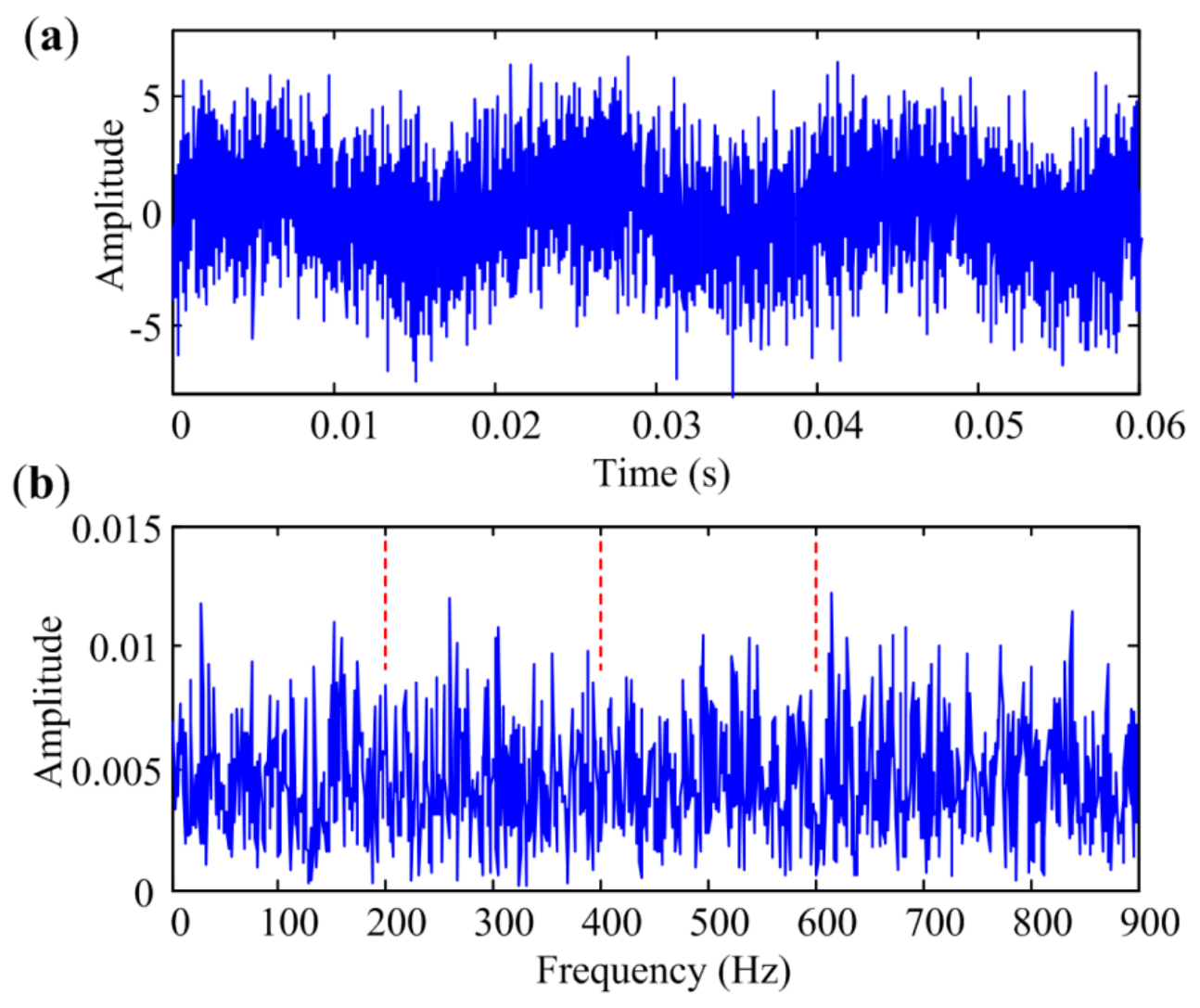
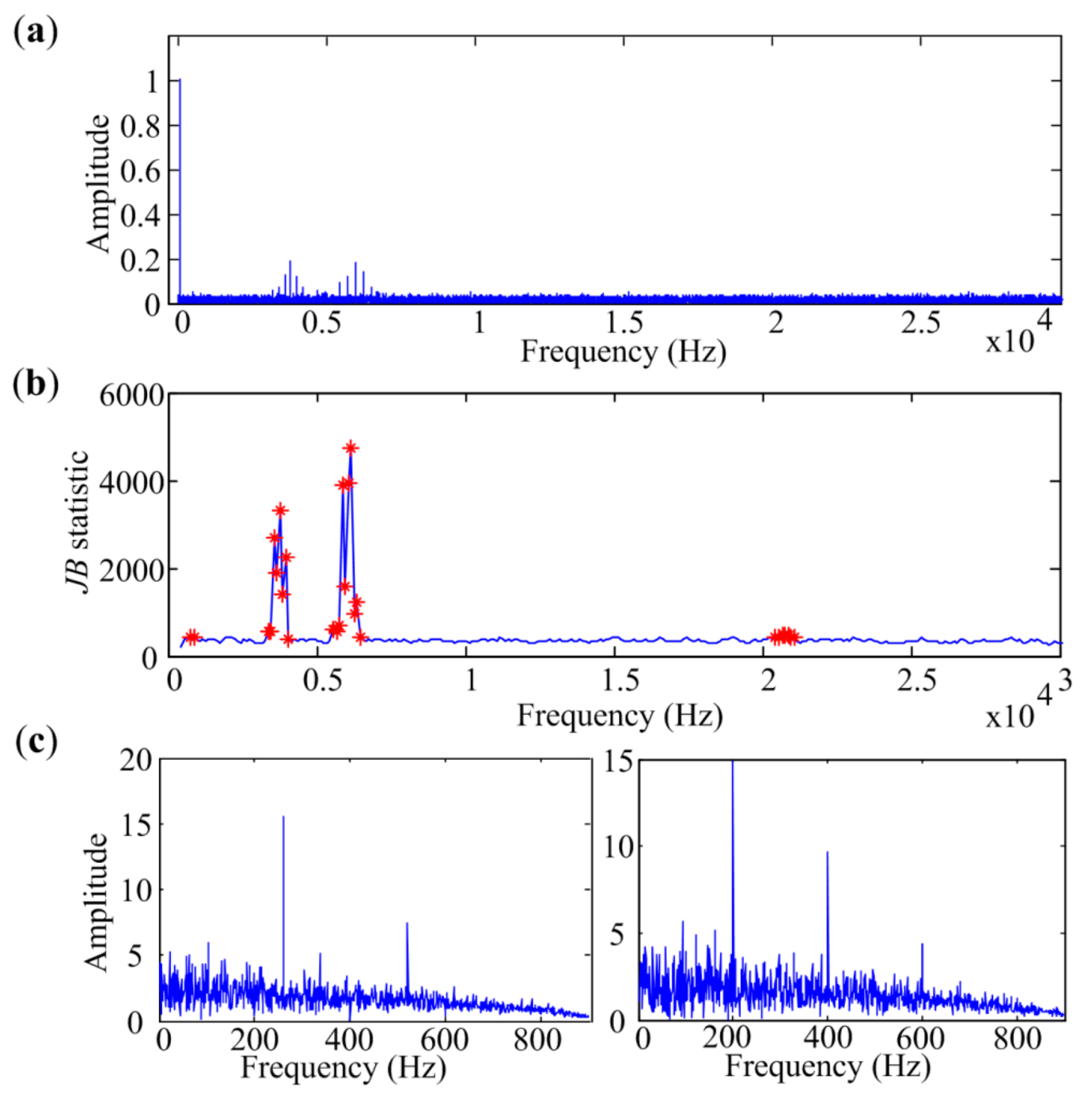

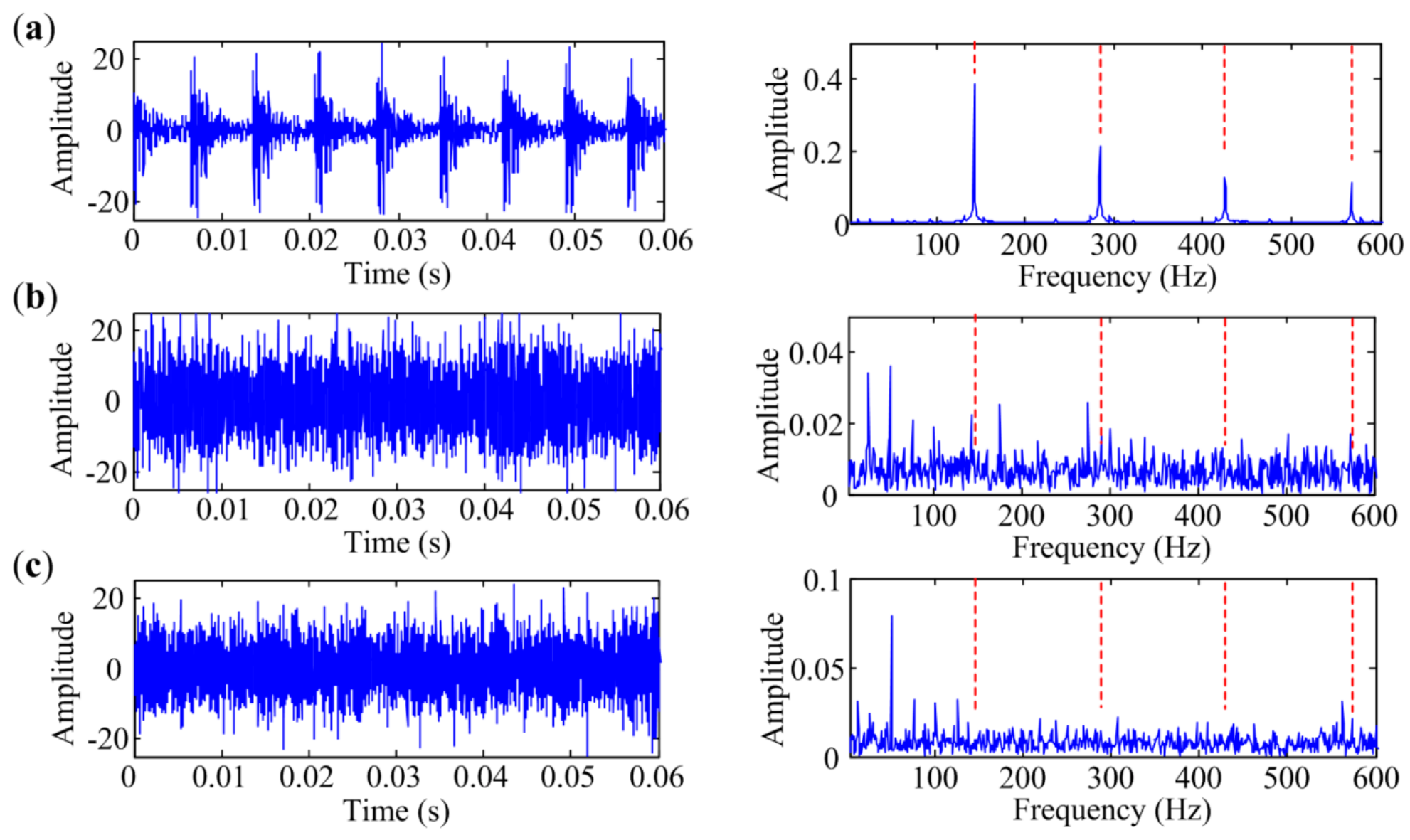


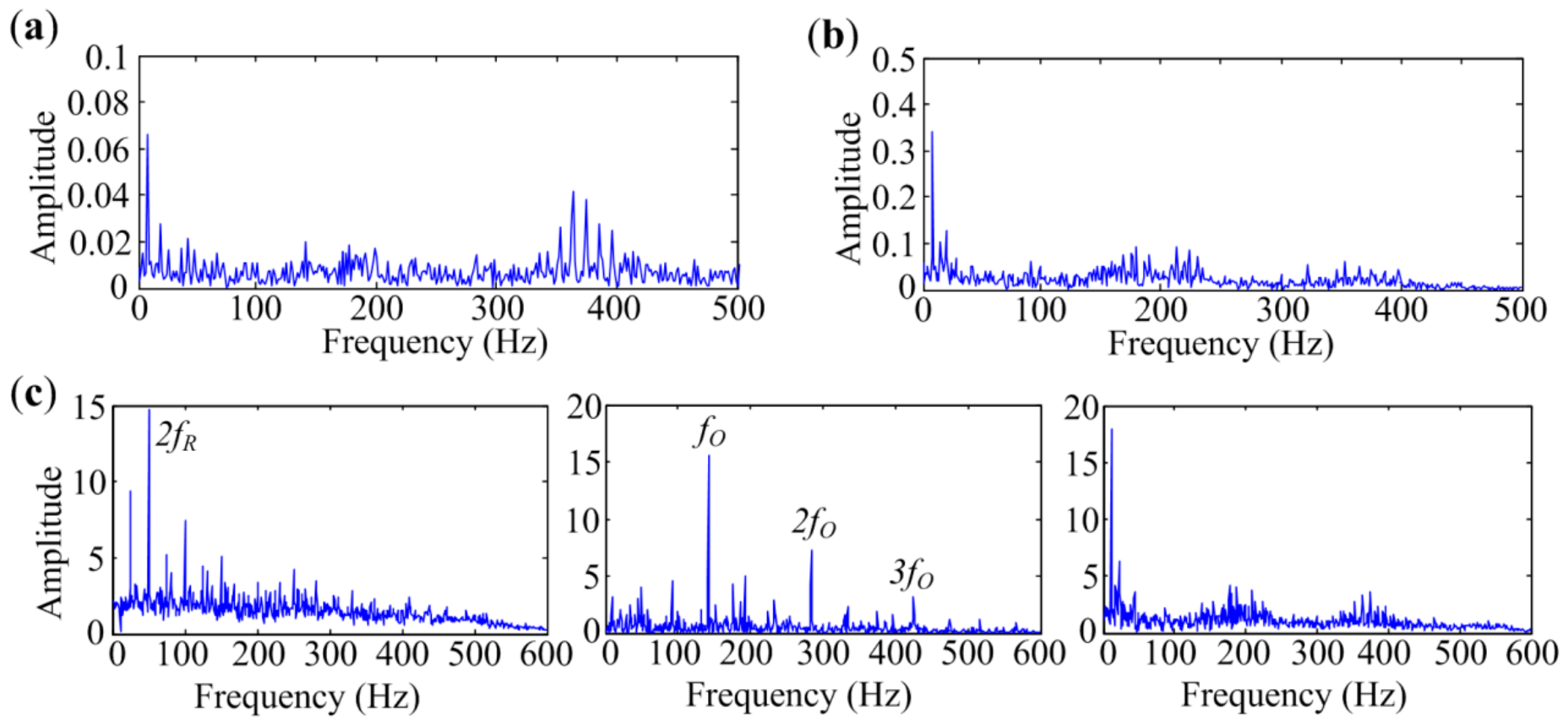
| Parameters | fs (Hz) | fr (Hz) | Aj | Β | T (s) | SNR (dB) |
|---|---|---|---|---|---|---|
| values | 65,536 | 3800 | 1.0 | 1000 | 0.005 | −20 |
| Type | Inside Diameter | Outside Diameter | Ball Diameter | Number of Balls | BPFI fI (Hz) | BPFO fO (Hz) |
|---|---|---|---|---|---|---|
| 6010 | 50 | 80 | 9 | 13 | 7.4fR | 5.6fR |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, J.; Shi, T.; Zhou, H.; Xuan, J.; Zhang, Y. Multiband Envelope Spectra Extraction for Fault Diagnosis of Rolling Element Bearings. Sensors 2018, 18, 1466. https://doi.org/10.3390/s18051466
Duan J, Shi T, Zhou H, Xuan J, Zhang Y. Multiband Envelope Spectra Extraction for Fault Diagnosis of Rolling Element Bearings. Sensors. 2018; 18(5):1466. https://doi.org/10.3390/s18051466
Chicago/Turabian StyleDuan, Jie, Tielin Shi, Hongdi Zhou, Jianping Xuan, and Yongxiang Zhang. 2018. "Multiband Envelope Spectra Extraction for Fault Diagnosis of Rolling Element Bearings" Sensors 18, no. 5: 1466. https://doi.org/10.3390/s18051466
APA StyleDuan, J., Shi, T., Zhou, H., Xuan, J., & Zhang, Y. (2018). Multiband Envelope Spectra Extraction for Fault Diagnosis of Rolling Element Bearings. Sensors, 18(5), 1466. https://doi.org/10.3390/s18051466






