A Novel Nonlinear Piezoelectric Energy Harvesting System Based on Linear-Element Coupling: Design, Modeling and Dynamic Analysis
Abstract
:1. Introduction
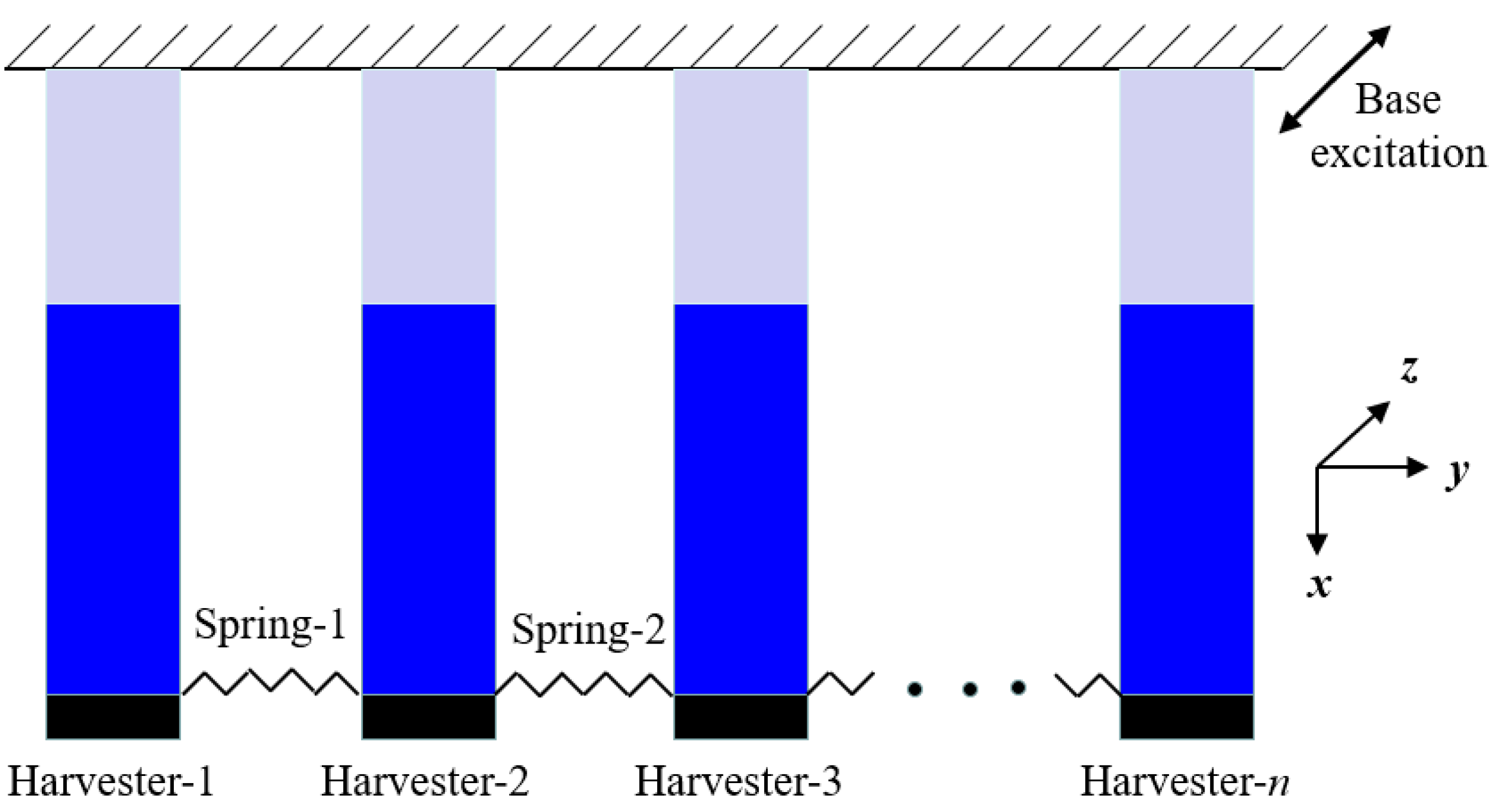
2. Concept and Modeling
3. Case Study for Verifying Energy Harvesting Improvement
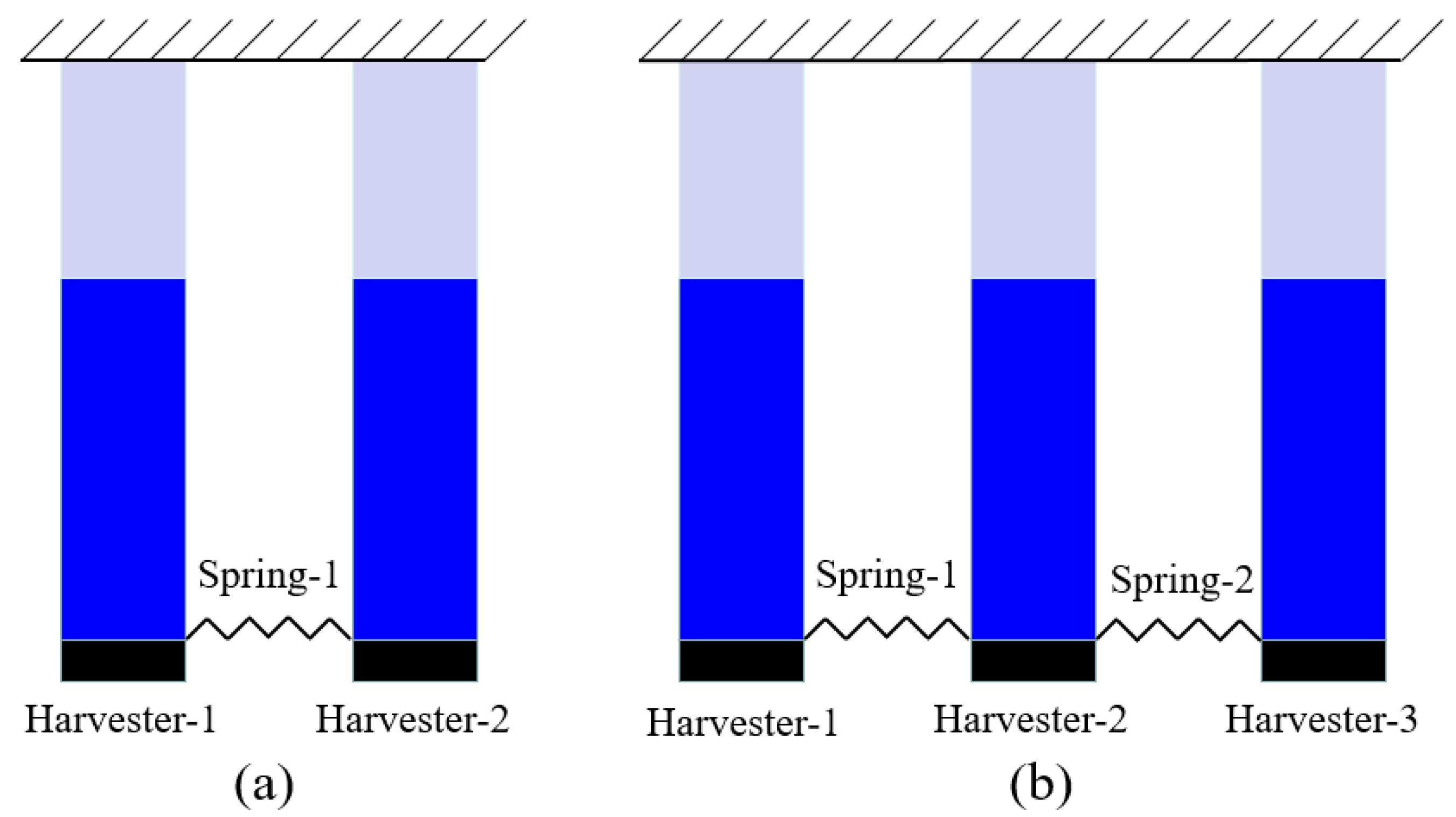
3.1. The NPEHS-1 with Two Energy Harvesters
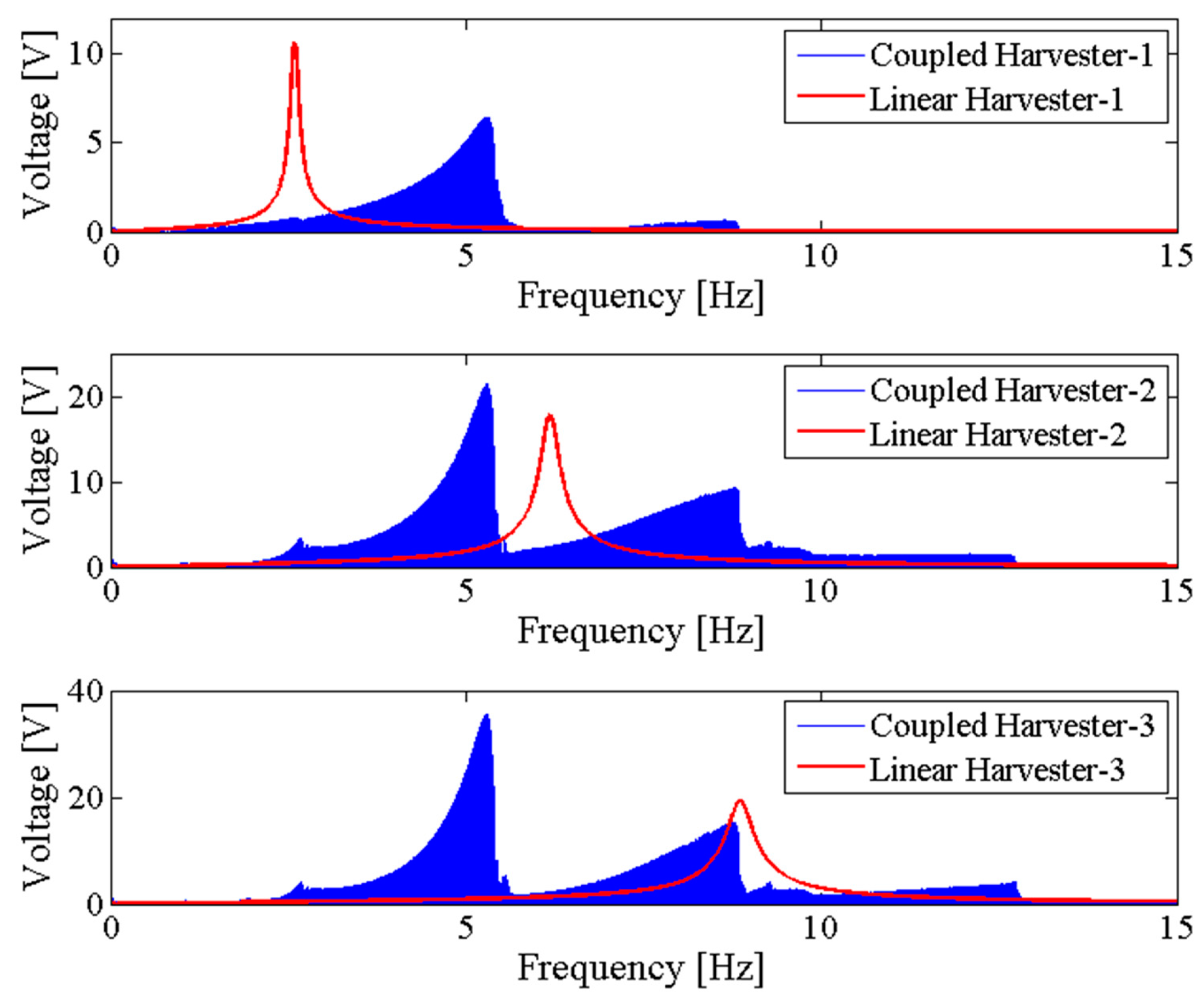
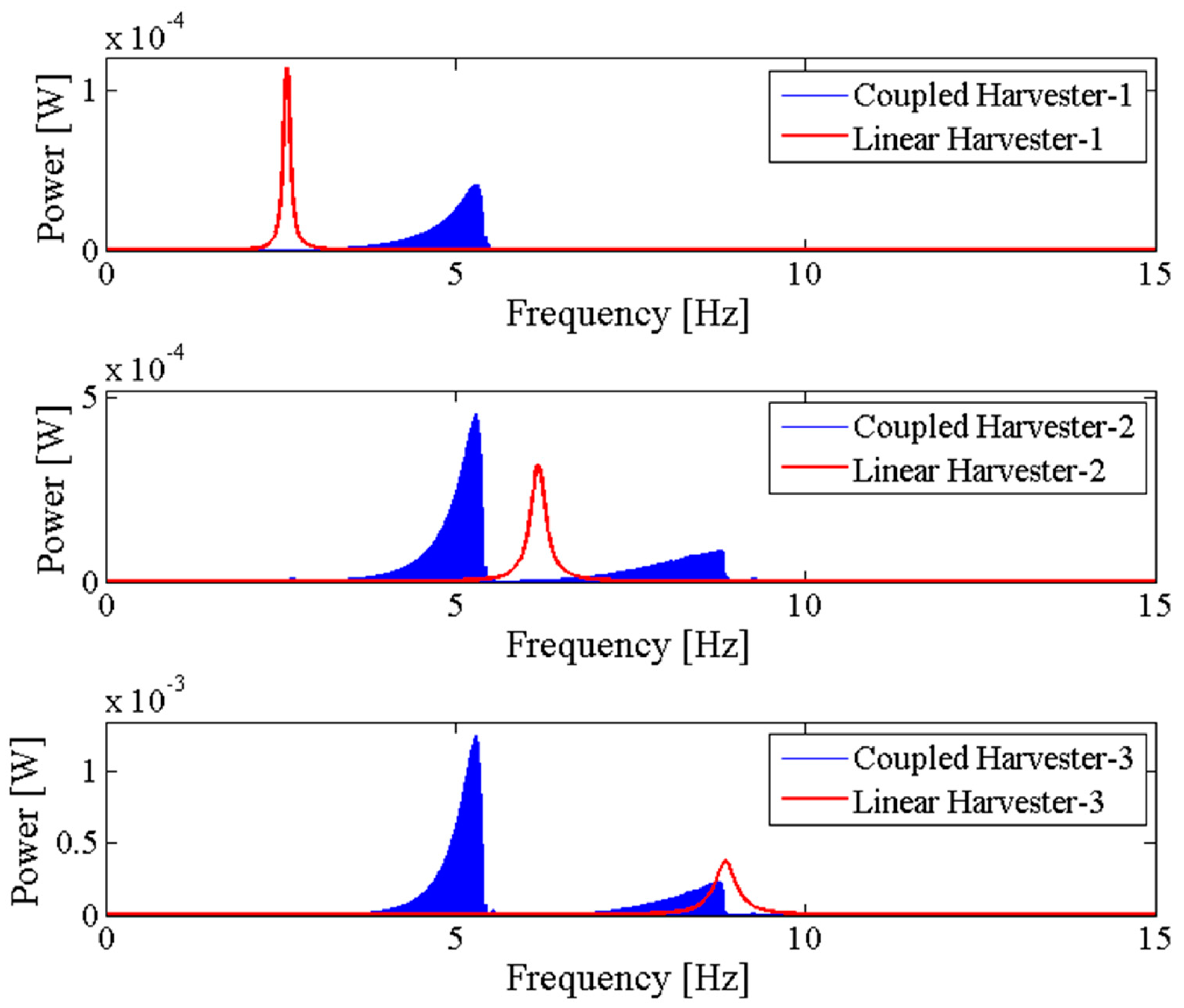
3.2. The NPEHS-2 with Three Energy Harvesters
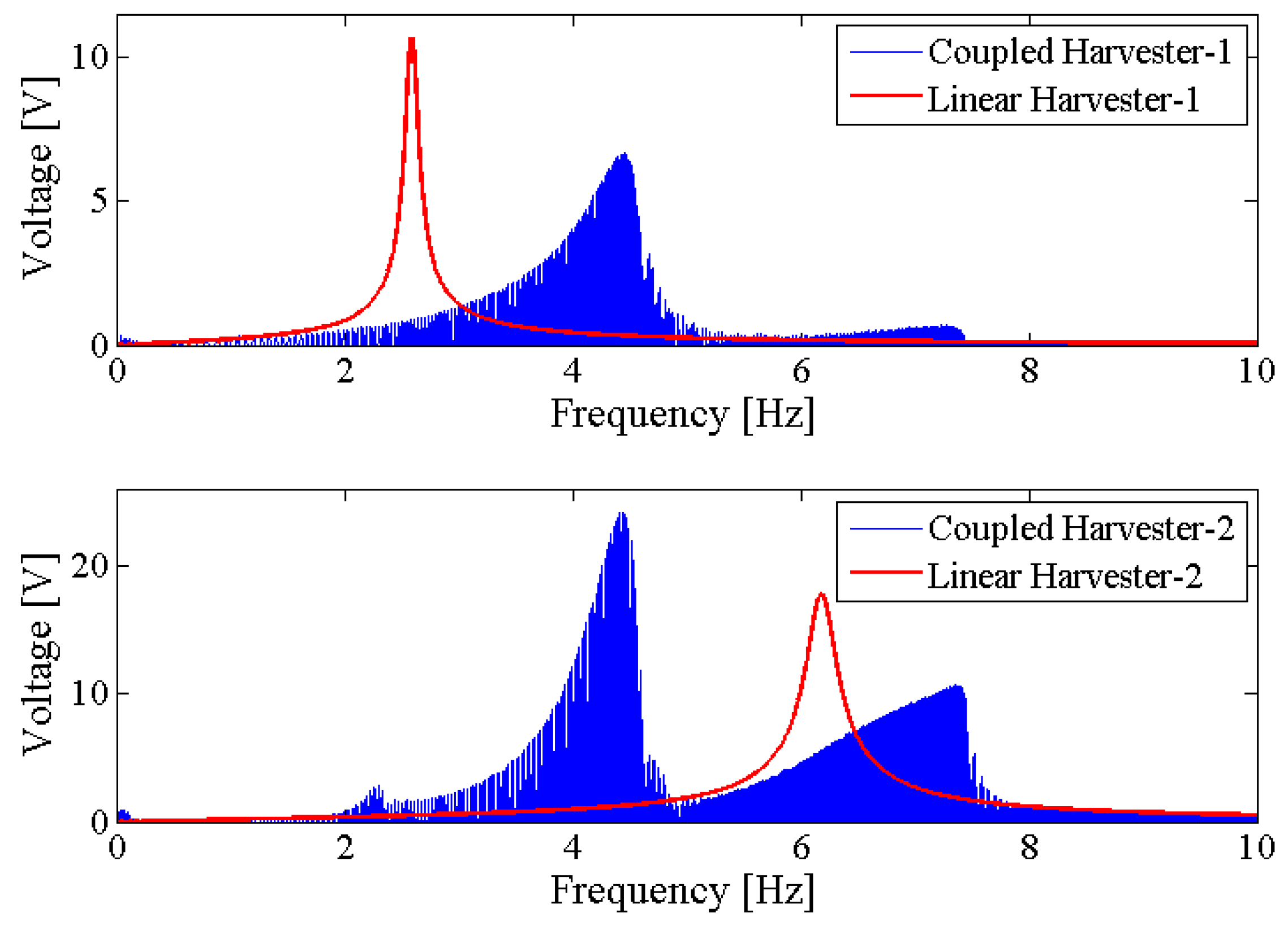
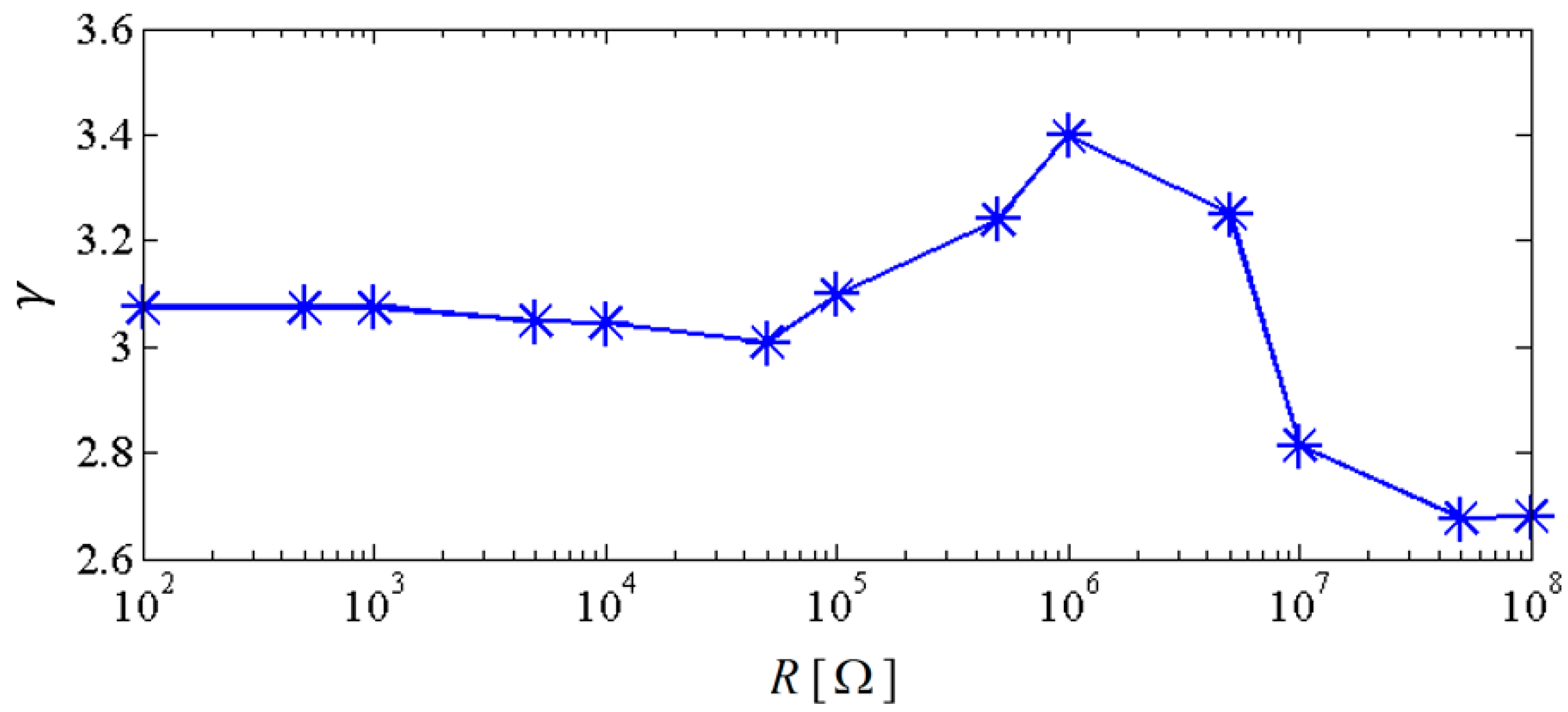
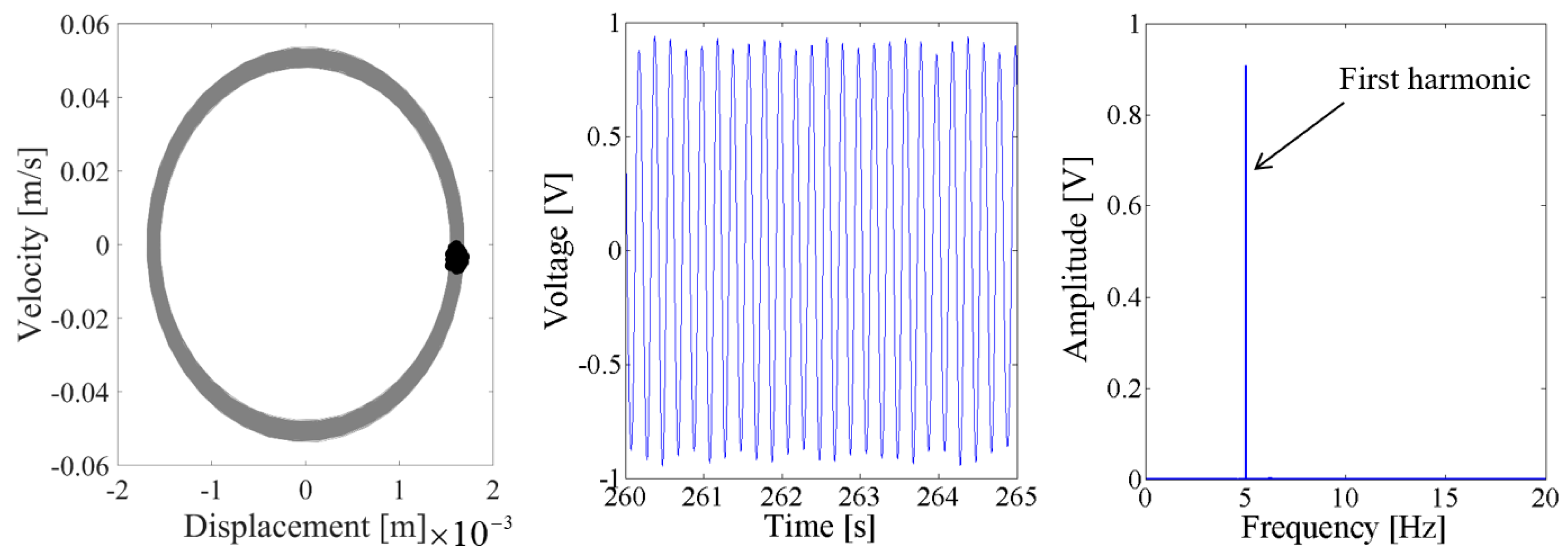
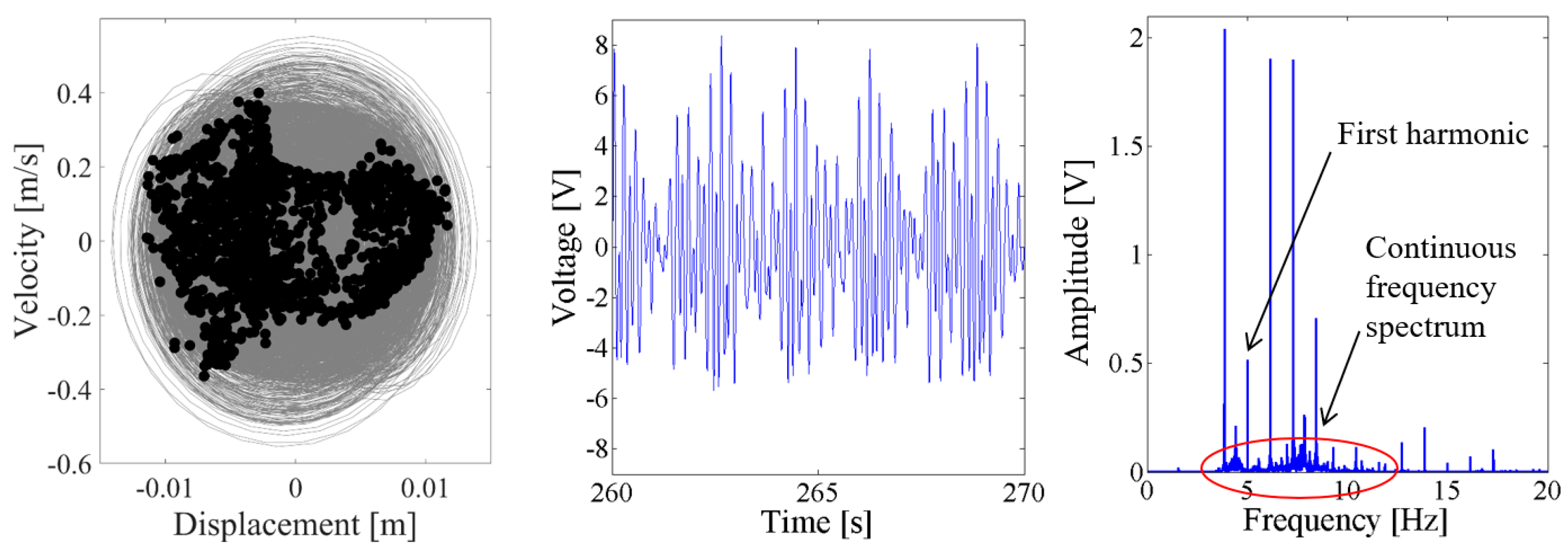
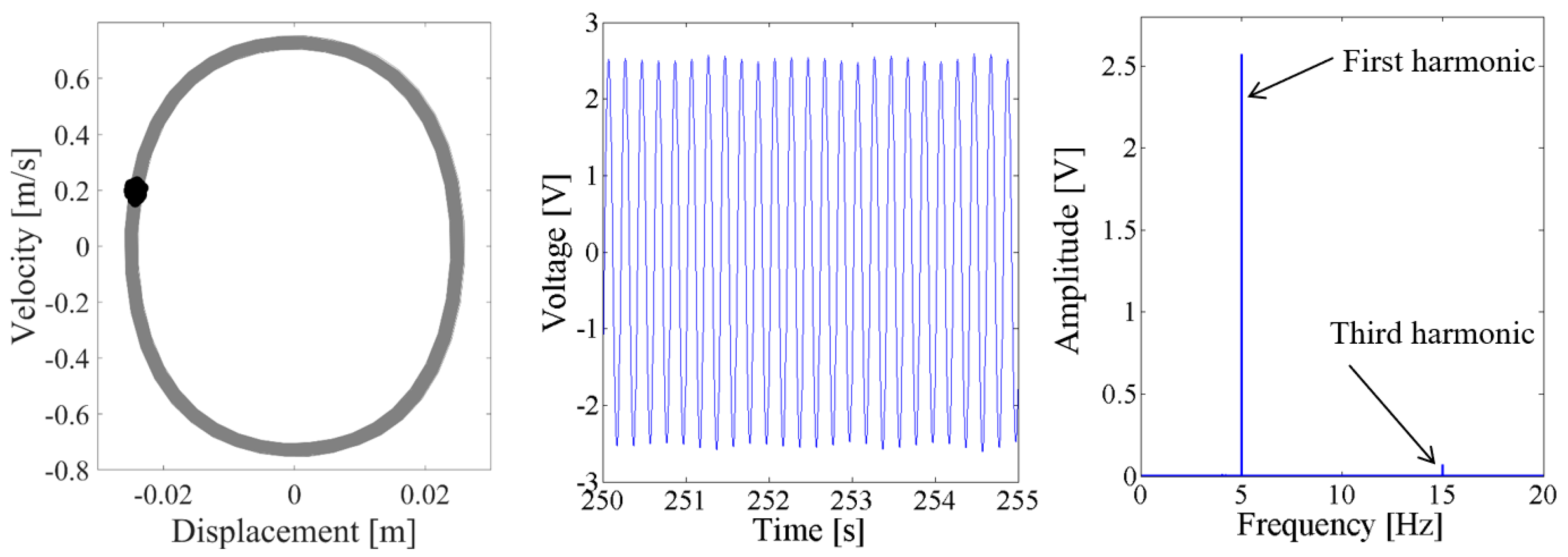
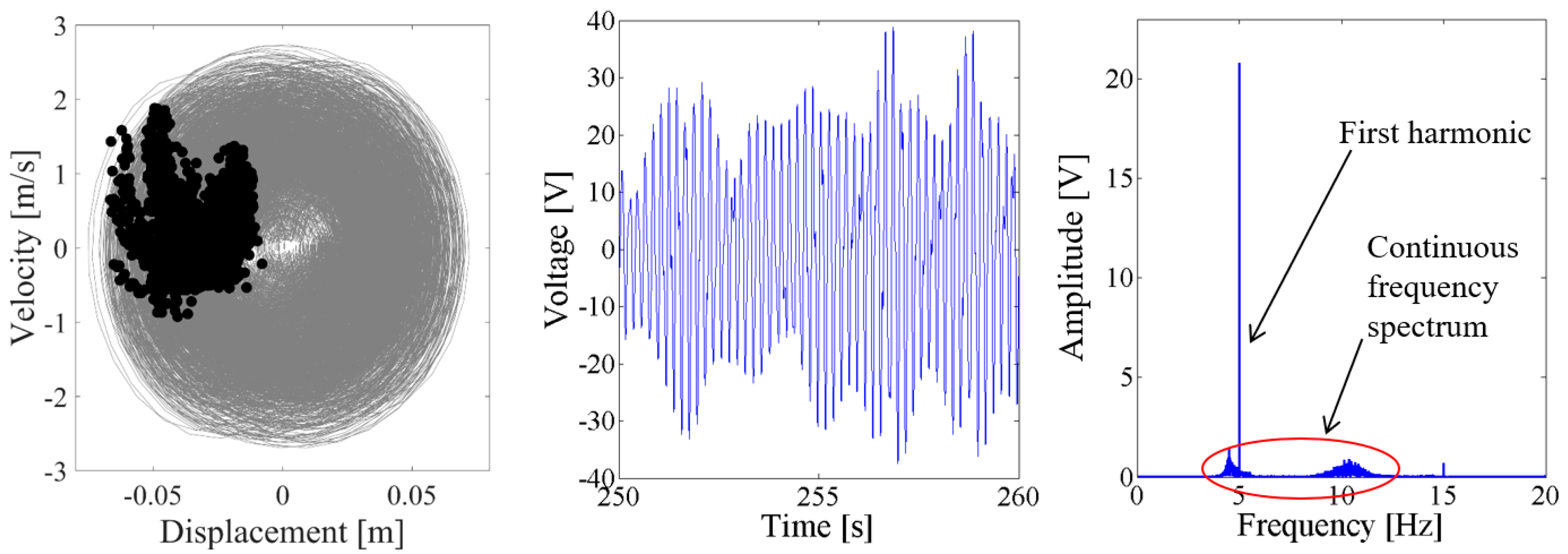
4. Nonlinear Dynamic Analysis
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
References
- Roundy, S.; Wright, P.K. A piezoelectric vibration based generator for wireless electronics. Smart Mater. Struct. 2004, 13, 1131. [Google Scholar] [CrossRef]
- Ho, S.C.M.; Li, W.; Wang, B.; Song, G. A load measuring anchor plate for rock bolt using fiber optic sensor. Smart Mater. Struct. 2017, 26, 057003. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Piezoelectric Energy Harvesting; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Luo, M.; Li, W.; Wang, B.; Fu, Q.; Song, G. Measurement of the Length of Installed Rock Bolt Based on Stress Wave Reflection by Using a Giant Magnetostrictive (GMS) Actuator and a PZT Sensor. Sensors 2017, 17, 444. [Google Scholar] [CrossRef] [PubMed]
- Hou, Q.; Ren, L.; Jiao, W.; Zou, P.; Song, G. An improved negative pressure wave method for natural gas pipeline leak location using FBG based strain sensor and wavelet transform. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Fu, H.; Chen, G.; Bai, N. Electrode Coverage Optimization for Piezoelectric Energy Harvesting from Tip Excitation. Sensors 2018, 18, 804. [Google Scholar] [CrossRef] [PubMed]
- Tao, K.; Tang, L.; Wu, J.; Lye, S.W.; Chang, H.; Miao, J. Investigation of multimodal electret-based MEMS energy harvester with impact-induced nonlinearity. J. Microelectromech. Syst. 2018, 27, 276–288. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations. Smart Mater. Struct. 2009, 18, 025009. [Google Scholar] [CrossRef]
- Song, G.; Li, H.; Gajic, B.; Zhou, W.; Chen, P.; Gu, H. Wind turbine blade health monitoring with piezoceramic-based wireless sensor network. Int. J. Smart Nano Mater. 2013, 4, 150–166. [Google Scholar] [CrossRef]
- Ho, S.C.M.; Ren, L.; Li, H.N.; Song, G. A fiber Bragg grating sensor for detection of liquid water in concrete structures. Smart Mater. Struct. 2013, 22, 055012. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, X.; Chen, W.; Xu, D. A bonded-type piezoelectric actuator using the first and second bending vibration modes. IEEE. Trans. Ind. Electron. 2016, 63, 1676–1683. [Google Scholar] [CrossRef]
- Song, G.; Li, W.; Wang, B.; Ho, S.C.M. A review of rock bolt monitoring using smart sensors. Sensors 2017, 17, 776. [Google Scholar] [CrossRef] [PubMed]
- Feng, Q.; Kong, Q.; Jiang, J.; Liang, Y.; Song, G. Detection of Interfacial Debonding in a Rubber-Steel-Layered Structure Using Active Sensing Enabled by Embedded Piezoceramic Transducers. Sensors 2017, 17, 2001. [Google Scholar] [CrossRef] [PubMed]
- Kong, Q.; Fan, S.; Bai, X.; Mo, Y.L.; Song, G. A novel embeddable spherical smart aggregate for structural health monitoring: Part I. Fabrication and electrical characterization. Smart Mater. Struct. 2017, 26, 095050. [Google Scholar] [CrossRef]
- Liu, Y.; Yan, J.; Xu, D.; Chen, W.; Yang, X.; Tian, X. An I-shape linear piezoelectric actuator using resonant type longitudinal vibration transducers. Mechatronics 2016, 40, 87–95. [Google Scholar] [CrossRef]
- Lu, G.; Li, Y.; Wang, T.; Xiao, H.; Huo, L.; Song, G. A multi-delay-and-sum imaging algorithm for damage detection using piezoceramic transducers. J. Intell. Mater. Syst. Struct. 2017, 28, 1150–1159. [Google Scholar] [CrossRef]
- Luo, M.; Li, W.; Wang, J.; Wang, N.; Chen, X.; Song, G. Development of a Novel Guided Wave Generation System Using a Giant Magnetostrictive Actuator for Nondestructive Evaluation. Sensors 2018, 18, 779. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Ho, S.C.M.; Patil, D.; Song, G. Acoustic emission monitoring and finite element analysis of debonding in fiber-reinforced polymer rebar reinforced concrete. Struct. Health Monit. 2017, 16, 674–681. [Google Scholar] [CrossRef]
- Cha, Y.; Hong, J.; Lee, J.; Park, J.M.; Kim, K. Flexible piezoelectric energy harvesting from mouse click motions. Sensors 2016, 16, 1045. [Google Scholar] [CrossRef] [PubMed]
- Wickenheiser, A.M. Eigensolution of piezoelectric energy harvesters with geometric discontinuities: Analytical modeling and validation. J. Intell. Mater. Syst. Struct. 2013, 24, 729–744. [Google Scholar] [CrossRef]
- Zhou, S.; Chen, W.; Malakooti, M.H.; Cao, J.; Inman, D.J. Design and modeling of a flexible longitudinal zigzag structure for enhanced vibration energy harvesting. J. Intell. Mater. Syst. Struct. 2017, 28, 367–380. [Google Scholar] [CrossRef]
- Wang, X.; Shi, Z.; Wang, J.; Xiang, H. A stack-based flex-compressive piezoelectric energy harvesting cell for large quasi-static loads. Smart Mater. Struct. 2016, 25, 055005. [Google Scholar] [CrossRef]
- Song, R.; Shan, X.; Lv, F.; Xie, T. A Novel Piezoelectric Energy Harvester Using the Macro Fiber Composite Cantilever with a Bicylinder in Water. Appl. Sci. 2015, 5, 1942–1954. [Google Scholar] [CrossRef]
- Liang, J.; Liao, W.H. Improved design and analysis of self-powered synchronized switch interface circuit for piezoelectric energy harvesting systems. IEEE. Trans. Ind. Electron. 2012, 59, 1950–1960. [Google Scholar] [CrossRef]
- Lan, C.; Tang, L.; Harne, R.L. Comparative methods to assess harmonic response of nonlinear piezoelectric energy harvesters interfaced with AC and DC circuits. J. Sound Vib. 2018, 421, 61–78. [Google Scholar] [CrossRef]
- Zou, H.; Zhang, W.; Li, W.; Wei, K.; Hu, K.; Peng, Z.; Meng, G. A broadband compressive-mode vibration energy harvester enhanced by magnetic force intervention approach. Appl. Phys. Lett. 2017, 110, 502001. [Google Scholar] [CrossRef]
- Xu, Z.; Shan, X.; Yang, H.; Wang, W.; Xie, T. Parametric Analysis and Experimental Verification of a Hybrid Vibration Energy Harvester Combining Piezoelectric and Electromagnetic Mechanisms. Micromachines 2017, 8, 189. [Google Scholar] [CrossRef]
- Harne, R.L.; Thota, M.; Wang, K.W. Bistable energy harvesting enhancement with an auxiliary linear oscillator. Smart Mater. Struct. 2013, 22, 125028. [Google Scholar] [CrossRef]
- Yan, Z.; Lei, H.; Tan, T.; Sun, W.; Huang, W. Nonlinear analysis for dual-frequency concurrent energy harvesting. Mech. Syst. Signal Process. 2018, 104, 514–535. [Google Scholar] [CrossRef]
- Daqaq, M.F.; Masana, R.; Erturk, A.; Quinn, D.D. On the role of nonlinearities in vibratory energy harvesting: A critical review and discussion. Appl. Mech. Rev. 2014, 66, 040801. [Google Scholar] [CrossRef]
- Wei, C.; Jing, X. A comprehensive review on vibration energy harvesting: Modelling and realization. Renew. Sustain. Energy Rev. 2017, 74, 1–18. [Google Scholar] [CrossRef]
- Yang, Z.; Zhu, Y.; Zu, J. Theoretical and experimental investigation of a nonlinear compressive-mode energy harvester with high power output under weak excitations. Smart Mater. Struct. 2015, 24, 025028. [Google Scholar] [CrossRef]
- Fang, Z.; Zhang, Y.; Li, X.; Ding, H.; Chen, L. Complexification-Averaging Analysis on a Giant Magnetostrictive Harvester Integrated With a Nonlinear Energy Sink. J. Vib. Acoust. 2018, 140, 021009. [Google Scholar] [CrossRef]
- Fang, Z.; Zhang, Y.; Li, X.; Ding, H.; Chen, L. Integration of a nonlinear energy sink and a giant magnetostrictive energy harvester. J. Sound Vib. 2017, 391, 35–49. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Barsallo, N. Comparative modeling of low-frequency piezomagnetoelastic energy harvesters. J. Intell. Mater. Syst. Struct. 2014, 25, 1771–1785. [Google Scholar] [CrossRef]
- Stanton, S.C.; McGehee, C.C.; Mann, B.P. Reversible hysteresis for broadband magnetopiezoelastic energy harvesting. Appl. Phys. Lett. 2009, 95, 174103. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Erturk, A.; Lin, J. Enhanced broadband piezoelectric energy harvesting using rotatable magnets. Appl. Phys. Lett. 2013, 102, 173901. [Google Scholar] [CrossRef]
- Deng, W.; Wang, Y. Systematic parameter study of a nonlinear electromagnetic energy harvester with matched magnetic orientation: Numerical simulation and experimental investigation. Mech. Syst. Signal Process. 2017, 85, 591–600. [Google Scholar] [CrossRef]
- Sebald, G.; Kuwano, H.; Guyomar, D.; Ducharne, B. Simulation of a Duffing oscillator for broadband piezoelectric energy harvesting. Smart Mater. Struct. 2011, 20, 075022. [Google Scholar] [CrossRef]
- Cottone, F.; Vocca, H.; Gammaitoni, L. Nonlinear energy harvesting. Phys. Rev. Lett. 2009, 102, 080601. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.; Chen, Z.; Xiong, Y.; Shi, H.; Yang, Y. A high-efficiency, self-powered nonlinear interface circuit for bi-stable rotating piezoelectric vibration energy harvesting with nonlinear magnetic force. Int. J. Appl. Electromagn. 2016, 51, 235–248. [Google Scholar] [CrossRef]
- Borowiec, M.; Rysak, A.; Betts, D.N.; Bowen, C.R.; Kim, H.A.; Litak, G. Complex response of a bistable laminated plate: Multiscale entropy analysis. Eur. Phys. J. Plus 2014, 129, 1–7. [Google Scholar] [CrossRef]
- Lan, C.; Qin, W. Enhancing ability of harvesting energy from random vibration by decreasing the potential barrier of bistable harvester. Mech. Syst. Signal Process. 2017, 85, 71–81. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Liu, S.; Wang, W.; Lin, J. Modeling and experimental verification of doubly nonlinear magnet-coupled piezoelectric energy harvesting from ambient vibration. Smart Mater. Struct. 2015, 24, 055008. [Google Scholar] [CrossRef]
- Stanton, S.C.; McGehee, C.C.; Mann, B.P. Nonlinear dynamics for broadband energy harvesting: Investigation of a bistable piezoelectric inertial generator. Physica D 2010, 239, 640–653. [Google Scholar] [CrossRef]
- Gao, Y.; Leng, Y.; Fan, S.; Lai, Z. Performance of bistable piezoelectric cantilever vibration energy harvesters with an elastic support external magnet. Smart Mater. Struct. 2014, 23, 095003. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Inman, D.J.; Lin, J.; Liu, S.; Wang, Z. Broadband tristable energy harvester: Modeling and experiment verification. Appl. Energy 2014, 133, 33–39. [Google Scholar] [CrossRef]
- Li, H.; Qin, W.; Lan, C.; Deng, W.; Zhou, Z. Dynamics and coherence resonance of tri-stable energy harvesting system. Smart Mater. Struct. 2015, 25, 015001. [Google Scholar]
- Kim, P.; Son, D.; Seok, J. Triple-well potential with a uniform depth: Advantageous aspects in designing a multi-stable energy harvester. Appl. Phys. Lett. 2016, 108, 243902. [Google Scholar] [CrossRef]
- Panyam, M.; Daqaq, M.F. Characterizing the effective bandwidth of tri-stable energy harvesters. J. Sound Vib. 2017, 386, 336–358. [Google Scholar] [CrossRef]
- Leng, Y.; Tan, D.; Liu, J.; Zhang, Y.; Fan, S. Magnetic force analysis and performance of a tri-stable piezoelectric energy harvester under random excitation. J. Sound Vib. 2017, 406, 146–160. [Google Scholar] [CrossRef]
- Zhou, S.; Zuo, L. Nonlinear dynamic analysis of asymmetric tristable energy harvesters for enhanced energy harvesting. Commun. Nonlinear. Sci. Numer. Simul. 2018, 61, 271–284. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Litak, G.; Lin, J. Numerical analysis and experimental verification of broadband tristable energy harvesters. TM Tech. Mess. 2018. [Google Scholar] [CrossRef]
- Leland, E.S.; Wright, P.K. Resonance tuning of piezoelectric vibration energy scavenging generators using compressive axial preload. Smart Mater. Struct. 2006, 15, 1413–1420. [Google Scholar] [CrossRef]
- Shahruz, S.M. Design of mechanical band-pass filters for energy scavenging: Multi-degree-of-freedom models. J. Vib. Control 2008, 14, 753–768. [Google Scholar] [CrossRef]
- Kim, I.H.; Jung, H.J.; Lee, B.M.; Jang, S.J. Broadband energy-harvesting using a two degree-of-freedom vibrating body. Appl. Phys. Lett. 2011, 98, 214102. [Google Scholar] [CrossRef]
- Wu, H.; Tang, L.; Yang, Y.; Soh, C.K. A novel two-degrees-of-freedom piezoelectric energy harvester. J. Intell. Mater. Syst. Struct. 2013, 24, 357–368. [Google Scholar] [CrossRef]
- Kuch, B.; Karami, M.A. Powering Pacemakers with a Nonlinear Hybrid Rotary-Translational Energy Harvester. In Proceedings of the 2014 ASME on International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Buffalo, NY, USA, 17–20 August 2014. [Google Scholar]
- Liu, W.; Bade, A.; Formosa, F.; Wu, Y.P.; Agbossou, A. Novel piezoelectric bistable oscillator architecture for wideband vibration energy harvesting. Smart Mater. Struct. 2013, 22, 035013. [Google Scholar] [CrossRef]
- Chen, L.; Jiang, W. Internal resonance energy harvesting. J. Appl. Mech. 2015, 82, 031004. [Google Scholar] [CrossRef]
- Chen, L.; Jiang, W.; Panyam, M.; Daqaq, M.F. A broadband internally resonant vibratory energy harvester. J. Vib. Acoust. 2016, 138, 061007. [Google Scholar] [CrossRef]
- Xu, J.; Tang, J. Modeling and analysis of piezoelectric cantilever-pendulum system for multi-directional energy harvesting. J. Intell. Mater. Syst. Struct. 2016, 28, 323–338. [Google Scholar] [CrossRef]
- Li, H.; Yang, Z.; Zu, J.; Qin, W. Distributed parameter model and experimental validation of a compressive-mode energy harvester under harmonic excitations. AIP Adv. 2016, 6, 085310. [Google Scholar] [CrossRef]
- Wei, C.; Jing, X. Vibrational energy harvesting by exploring structural benefits and nonlinear characteristics. Commun. Nonlinear Sci. Numer. Simul. 2017, 48, 288–306. [Google Scholar] [CrossRef]
- Thompson, J.M.T.; Stewart, H.B. Nonlinear Dynamics and Chaos; John Wiley & Sons: New York, NY, USA, 2002. [Google Scholar]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; John Wiley & Sons: New York, NY, USA, 2008. [Google Scholar]
- Kovacic, I.; Brennan, M.J. The Duffing Equation: Nonlinear Oscillators and Their Behavior; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Liao, Y.; Sodano, H.A. Model of a single mode energy harvester and properties for optimal power generation. Smart Mater. Struct. 2008, 17, 065026. [Google Scholar] [CrossRef]
- Malakooti, M.H.; Sodano, H.A. Piezoelectric energy harvesting through shear mode operation. Smart Mater. Struct. 2015, 24, 055005. [Google Scholar] [CrossRef]
- Zhou, S.; Hobeck, J.D.; Cao, J.; Inman, D.J. Analytical and experimental investigation of flexible longitudinal zigzag structures for enhanced energy harvesting. Smart Mater. Struct. 2017, 26, 035008. [Google Scholar] [CrossRef]
- Inman, D.J. Engineering Vibration, 4th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2013. [Google Scholar]
- Masana, R.; Daqaq, M.F. Energy harvesting in the super-harmonic frequency region of a twin-well oscillator. J. Appl. Phys. 2012, 111, 044501. [Google Scholar] [CrossRef]
- Cao, J.; Zhou, S.; Inman, D.J.; Chen, Y. Chaos in the fractionally damped broadband piezoelectric energy generator. Nonlinear Dyn. 2015, 80, 1705–1719. [Google Scholar] [CrossRef]
- Yan, B.; Wang, K.; Hu, Z.; Wu, C.; Zhang, X. Shunt damping vibration control technology: A review. Appl. Sci. 2017, 7, 494. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, S.; Zu, J.; Inman, D.J. High-Performance Piezoelectric Energy Harvesters and Their Applications. Joule 2018, 2, 642–697. [Google Scholar] [CrossRef]

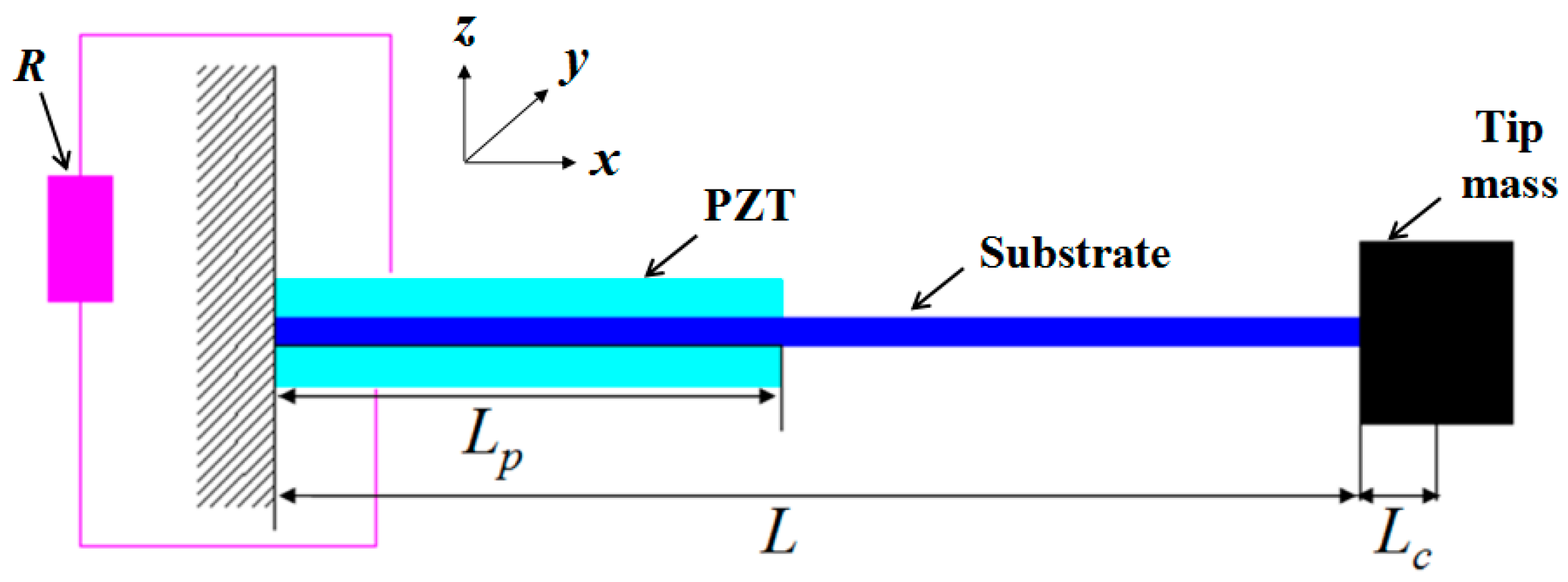









| L | Lp | Lc | b | hs | hp | |
|---|---|---|---|---|---|---|
| Harvester-1 | 80 | 20 | 5 | 15 | 0.10 | 0.5 |
| Harvester-2 | 80 | 20 | 5 | 15 | 0.18 | 0.5 |
| Harvester-3 | 80 | 20 | 5 | 15 | 0.23 | 0.5 |
| Substrate | ||
| Parameter | Symbol | Value |
| Young’s modulus | 125 GPa | |
| Density | 8250 kg/m3 | |
| Piezoelectric layers | ||
| Young’s modulus | 63 GPa | |
| Density | 7700 kg/m3 | |
| Coupling coefficient | −285 × 10−12 C/N | |
| Permittivity constant | 3200 | |
| Permittivity of free space | 8.854 × 10−12 F/m | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Yan, B.; Inman, D.J. A Novel Nonlinear Piezoelectric Energy Harvesting System Based on Linear-Element Coupling: Design, Modeling and Dynamic Analysis. Sensors 2018, 18, 1492. https://doi.org/10.3390/s18051492
Zhou S, Yan B, Inman DJ. A Novel Nonlinear Piezoelectric Energy Harvesting System Based on Linear-Element Coupling: Design, Modeling and Dynamic Analysis. Sensors. 2018; 18(5):1492. https://doi.org/10.3390/s18051492
Chicago/Turabian StyleZhou, Shengxi, Bo Yan, and Daniel J. Inman. 2018. "A Novel Nonlinear Piezoelectric Energy Harvesting System Based on Linear-Element Coupling: Design, Modeling and Dynamic Analysis" Sensors 18, no. 5: 1492. https://doi.org/10.3390/s18051492
APA StyleZhou, S., Yan, B., & Inman, D. J. (2018). A Novel Nonlinear Piezoelectric Energy Harvesting System Based on Linear-Element Coupling: Design, Modeling and Dynamic Analysis. Sensors, 18(5), 1492. https://doi.org/10.3390/s18051492






