A Novel Locating System for Cereal Plant Stem Emerging Points’ Detection Using a Convolutional Neural Network
Abstract
:1. Introduction
2. Materials and Methods
2.1. Field Experiment
2.2. Data Acquisition Platform
2.3. Convolutional Neural Network for Emergence Point Detection
2.3.1. Network Architecture
2.3.2. Marking Possible PSEPs
2.3.3. Training
2.3.4. Evaluation Method
3. Results
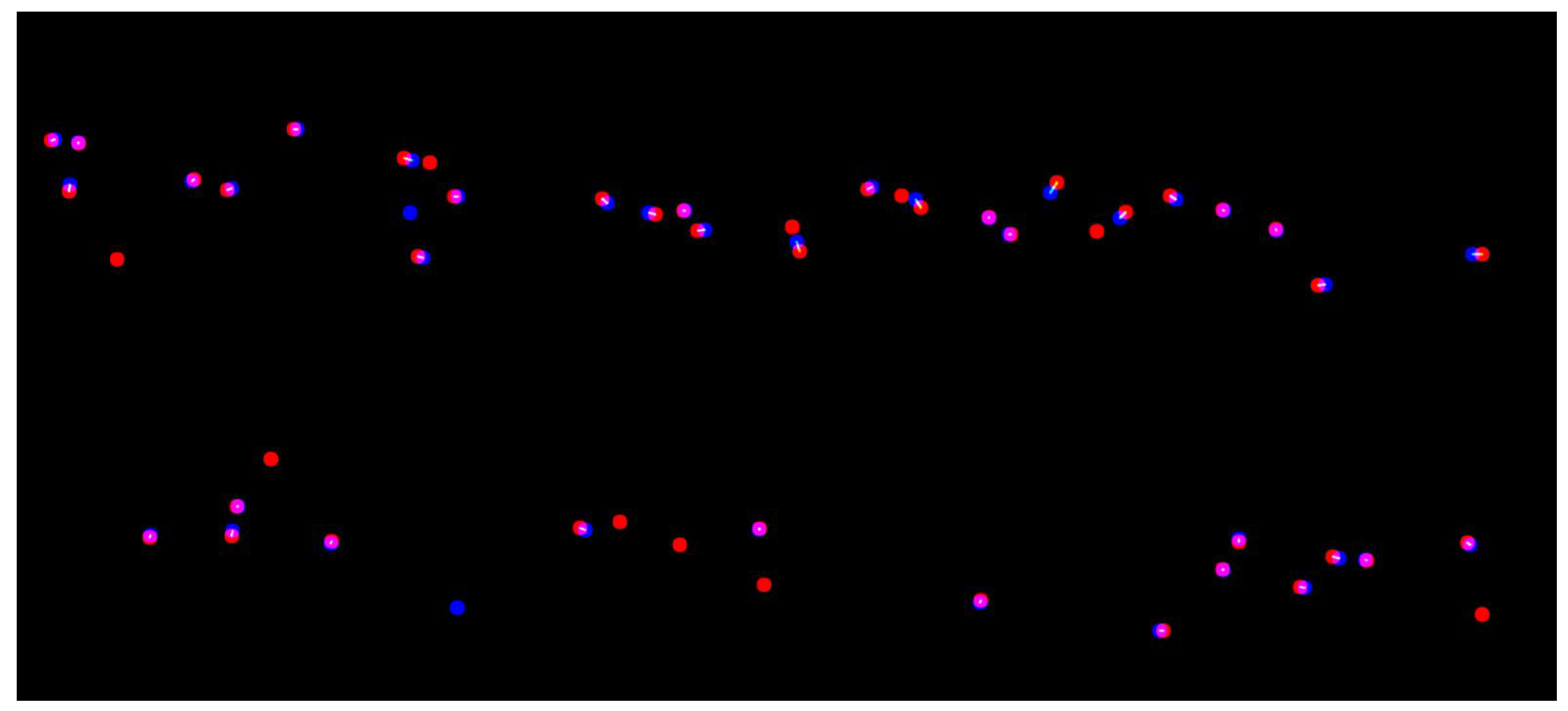
3.1. Selecting Images from the Dataset for Evaluation
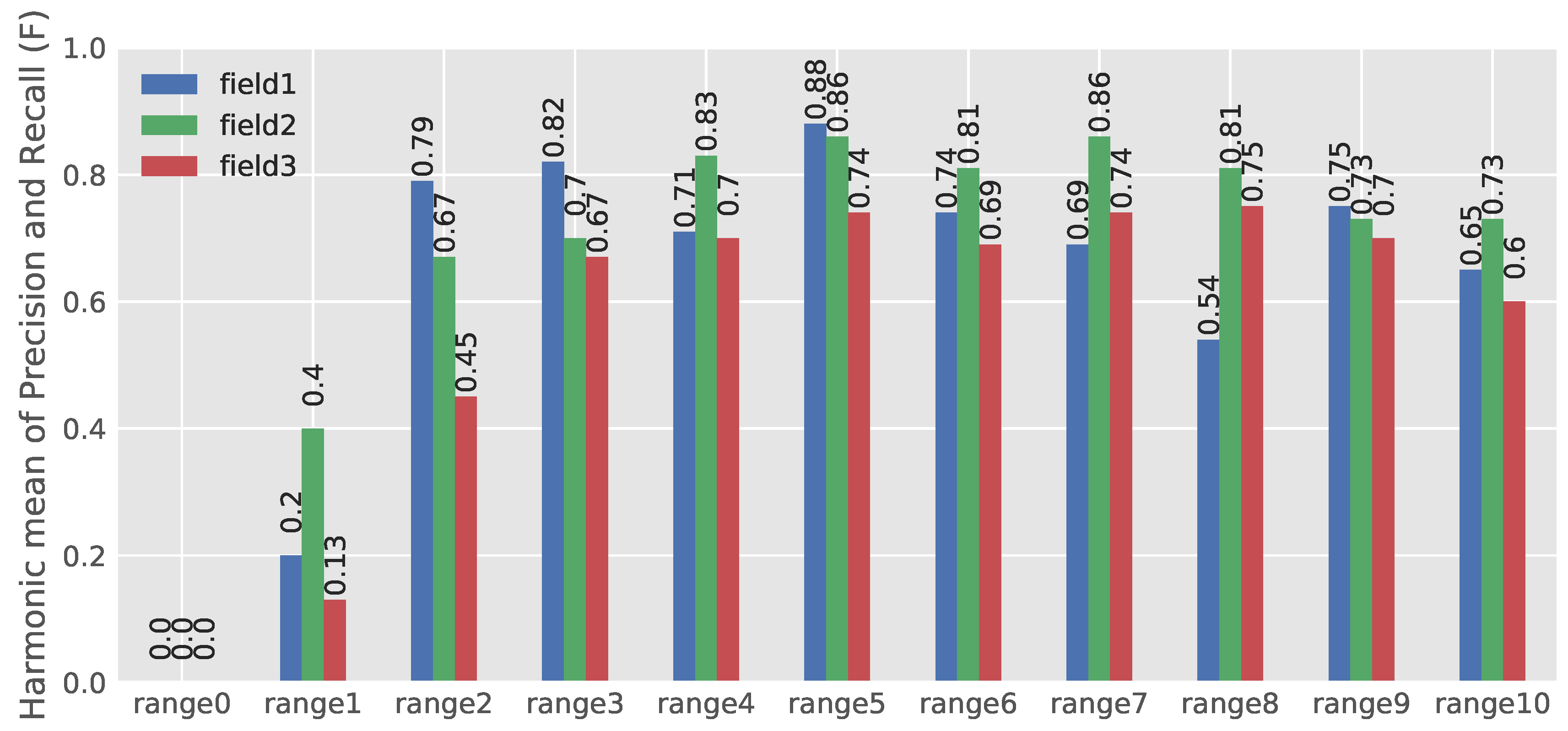
3.2. Evaluating the Developed Network
4. Discussion
5. Conclusions
- In this study, marking 212 images with possible PESPs for the training process took considerable time and required tedious work, so providing more annotated images would significantly enhance the generalized network proficiency. In future works, expanding the training dataset from various cereal fields would increase the chance of a successful application of the system in the operational phase.
- There was sometimes the problem of neighboring plants’ leaves’ coverage which made PSEPs’ identification hard, even for the trained eye. This problem was more intensive in the Field 3 dataset. To get rid of interfering leaves, data acquisition in an earlier growth stage with smaller leaves is recommended.
- In some cases, weeds were mistakenly predicted as actual crops, especially when they had a shape similar to real crops. In future studies, weeds can be subtracted from the captured image due to a pre-established map of weeds. The weeds’ map can be obtained by developing an FCN weed and crop classification model [26].
- Recently, high-resolution imagery obtained from a UAV at very low altitude was employed to develop a wheat plant density measuring system [16]. Investigating the use of UAV-based images in the developed PESP locating method in the future could be worthwhile.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lauer, J.G.; Rankin, M. Corn Response to Within Row Plant Spacing Variation. Agron. J. 2004, 96. [Google Scholar] [CrossRef]
- Martínez-Guanter, J.; Garrido-Izard, M.; Valero, C.; Slaughter, D.C.; Pérez-Ruiz, M. Optical Sensing to Determine Tomato Plant Spacing for Precise Agrochemical Application: Two Scenarios. Sensors 2017, 17. [Google Scholar] [CrossRef] [PubMed]
- Sangoi, L. Understanding plant density effects on maize growth and development: An important issue maximizes grain yield. Cienc. Rural 2001, 31. [Google Scholar] [CrossRef]
- Tang, L.; Tian, L.F. Plant identification in mosaicked crop row images for automatic emerged corn plant spacing measurement. Trans. ASABE 2008. [Google Scholar] [CrossRef]
- Murray, J.R.; Tullberg, J.N.; Basnet, B.B. Planters and Their Components: Types, Attributes, Functional Requirements, Classification and Description (ACIAR Monograph No. 121); Australian Centre for International Agricultural Research: Canberra, Australia, 2006; p. 178.
- Virk, S.S.; Fulton, J.P.; Porter, W.M.; Pate, G.L. Field Validation of Seed Meter Performance at Varying Seeding Rates and Ground Speeds; ASABE Paper No. 1701309; ASABE: St. Joseph, MI, USA, 2017; p. 1. [Google Scholar]
- Liu, S.; Baret, F.; Allard, D.; Jin, X.; Andrieu, B.; Burger, P.; Hemmerlé, M.; Comar, A. A method to estimate plant density and plant spacing heterogeneity: Application to wheat crops. Plant Methods 2017, 13, 38. [Google Scholar] [CrossRef] [PubMed]
- Xia, L.; Wang, X.; Geng, D.; Zhang, Q. Performance monitoring system for precision planter based on MSP430-CT171. In Proceedings of the International Conference on Computer and Computing Technologies in Agriculture, Nanchang, China, 22–25 October 2010; Springer: New York, NY, USA, 2010; pp. 158–165. [Google Scholar]
- Al-Mallahi, A.; Kataoka, T. Application of fibre sensor in grain drill to estimate seed flow under field operational conditions. Comput. Electron. Agric. 2016, 121, 412–419. [Google Scholar] [CrossRef]
- Midtiby, H.S.; Giselsson, T.M.; Jørgensen, R.N. Estimating the plant stem emerging points (PSEPs) of sugar beets at early growth stages. Biosyst. Eng. 2012, 111, 83–90. [Google Scholar] [CrossRef] [Green Version]
- Shrestha, D.; Steward, B. Automatic Corn Plant Population Measurement Using Machine Vision. In Proceedings of the 2001 ASAE Annual International Meeting, Sacramento, CA, USA, 30 July–1 August 2001; Volume 46, pp. 559–565. [Google Scholar]
- Tang, L.; Tian, L.F. Real-Time Crop Row Image Reconstruction for Automatic Emerged Corn Plant Spacing Measurement. Trans. ASABE 2008, 51, 1079–1087. [Google Scholar] [CrossRef]
- Jin, J.; Tang, L. Corn plant sensing using real-time stereo vision. J. Field Robot. 2009, 26, 591–608. [Google Scholar] [CrossRef]
- Nakarmi, A.D.; Tang, L. Automatic inter-plant spacing sensing at early growth stages using a 3D vision sensor. Comput. Electron. Agric. 2012, 82, 23–31. [Google Scholar] [CrossRef]
- Nakarmi, A.D.; Tang, L. Within-row spacing sensing of maize plants using 3D computer vision. Biosyst. Eng. 2014, 125, 54–64. [Google Scholar] [CrossRef]
- Jin, X.; Liu, S.; Baret, F.; Hemerlé, M.; Comar, A. Estimates of plant density of wheat crops at emergence from very low altitude UAV imagery. Remote Sens. Environ. 2017, 198, 105–114. [Google Scholar] [CrossRef]
- Liu, S.; Baret, F.; Andrieu, B.; Burger, P.; Hemmerlé, M. Estimation of Wheat Plant Density at Early Stages Using High Resolution Imagery. Front. Plant Sci. 2017, 8, 739. [Google Scholar] [CrossRef] [PubMed]
- Laursen, M.S.; Jørgensen, R.N.; Dyrmann, M.; Poulsen, R. RoboWeedSupport-Sub Millimeter Weed Image Acquisition in Cereal Crops with Speeds up till 50 Km/H. Int. J. Biol. Biomol. Agric. Food Biotechnol. Eng. 2017, 11, 317–321. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. arXiv, 2014; arXiv:1411.4038. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv, 2014; arXiv:1409.1556v6. [Google Scholar]
- Martin, D.R.; Fowlkes, C.C.; Malik, J. Learning to detect natural image boundaries using local brightness, color, and texture cues. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 530–549. [Google Scholar] [CrossRef] [PubMed]
- Teimouri, N.; Omid, M.; Mollazade, K.; Rajabipour, A. A novel artificial neural networks assisted segmentation algorithm for discriminating almond nut and shell from background and shadow. Comput. Electron. Agric. 2014, 105, 34–43. [Google Scholar] [CrossRef]
- Visa, G.P.; Salembier, P. Precision-Recall-Classification Evaluation Framework: Application to Depth Estimation on Single Images. In Computer Vision—ECCV 2014; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 648–662. [Google Scholar]
- Yazgi, A.; Degirmencioglu, A. Measurement of seed spacing uniformity performance of a precision metering unit as function of the number of holes on vacuum plate. Measurement 2014, 56, 128–135. [Google Scholar] [CrossRef]
- Kocher, M.F.; Lan, Y.; Chen, C.; Smith, J.A. Opto-electronic sensor system for rapid evaluation of planter seed spacing uniformity. Trans. ASAE 1998, 41, 237–245. [Google Scholar] [CrossRef]
- Dyrmann, M.; Mortensen, A.; Midtiby, H.; Nyholm Jørgensen, R. Pixel-Wise Classification of Weeds and Crops in Images by Using a Fully Convolutional Neural Network; Paper No. 608; CIGR: Liege, Belgium, 2016. [Google Scholar]














| Softmax-Thresholds | ||||||||
|---|---|---|---|---|---|---|---|---|
| P 00 SM 0.1 | P 00 SM 0.2 | P 00 SM 0.3 | P 00 SM 0.4 | P 00 SM 0.5 | P 00 SM 0.6 | P 00 SM 0.7 | P 00 SM 0.8 | P 00 SM 0.9 |
| P 50 SM 0.1 | P 50 SM 0.2 | P 50 SM 0.3 | P 50 SM 0.4 | P 50 SM 0.5 | P 50 SM 0.6 | P 50 SM 0.7 | P 50 SM 0.8 | P 50 SM 0.9 |
| P 75 SM 0.1 | P 75 SM 0.2 | P 75 SM 0.3 | P 75 SM 0.4 | P 75 SM 0.5 | P 75 SM 0.6 | P 75 SM 0.7 | P 75 SM 0.8 | P 75 SM 0.9 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karimi, H.; Skovsen, S.; Dyrmann, M.; Nyholm Jørgensen, R. A Novel Locating System for Cereal Plant Stem Emerging Points’ Detection Using a Convolutional Neural Network. Sensors 2018, 18, 1611. https://doi.org/10.3390/s18051611
Karimi H, Skovsen S, Dyrmann M, Nyholm Jørgensen R. A Novel Locating System for Cereal Plant Stem Emerging Points’ Detection Using a Convolutional Neural Network. Sensors. 2018; 18(5):1611. https://doi.org/10.3390/s18051611
Chicago/Turabian StyleKarimi, Hadi, Søren Skovsen, Mads Dyrmann, and Rasmus Nyholm Jørgensen. 2018. "A Novel Locating System for Cereal Plant Stem Emerging Points’ Detection Using a Convolutional Neural Network" Sensors 18, no. 5: 1611. https://doi.org/10.3390/s18051611
APA StyleKarimi, H., Skovsen, S., Dyrmann, M., & Nyholm Jørgensen, R. (2018). A Novel Locating System for Cereal Plant Stem Emerging Points’ Detection Using a Convolutional Neural Network. Sensors, 18(5), 1611. https://doi.org/10.3390/s18051611






