Multi-Camera Imaging System for UAV Photogrammetry
Abstract
:1. Introduction
Related Works
2. Methodology
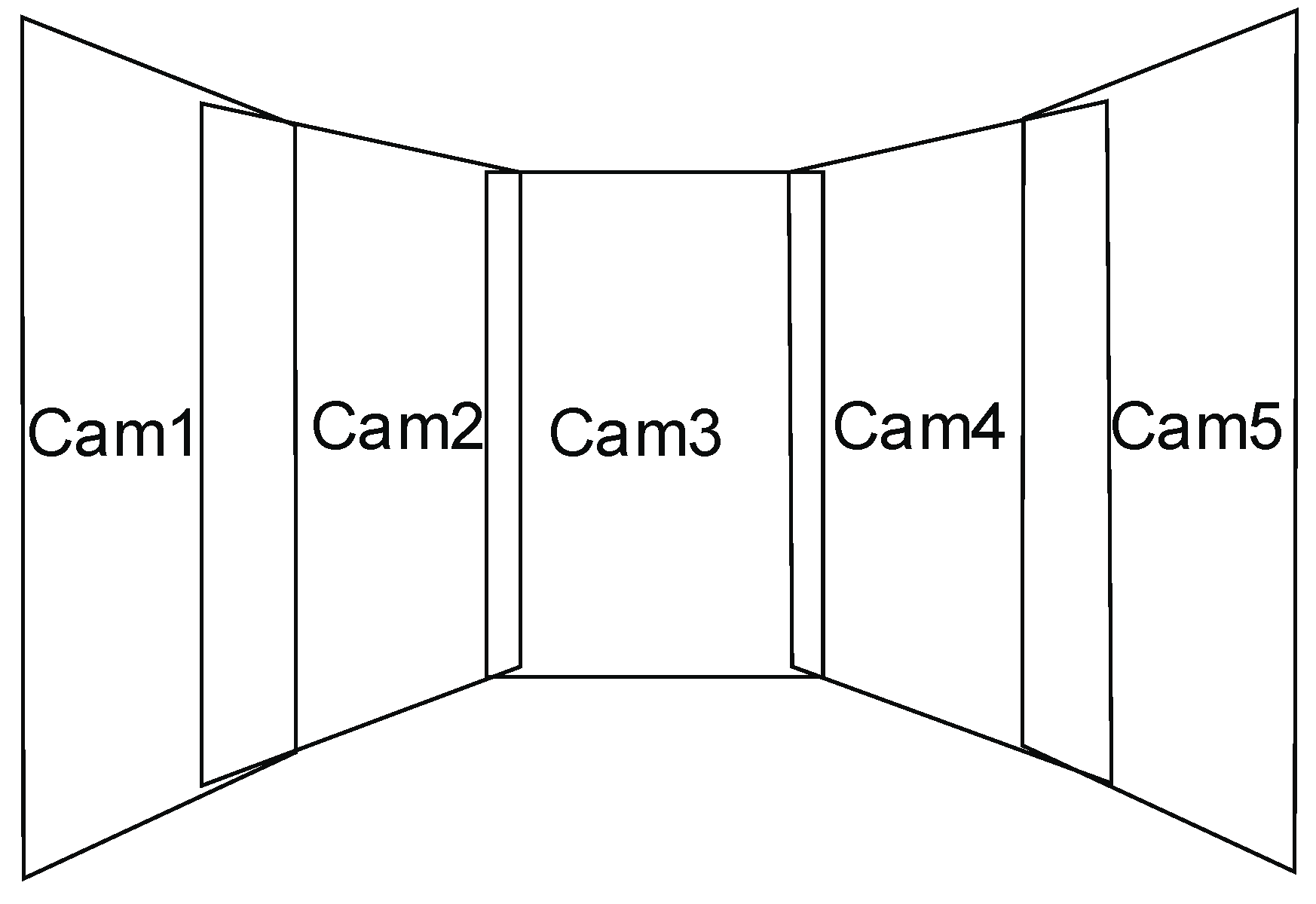
2.1. Description of UAV Multi-Camera Imaging System
Camera Specifications
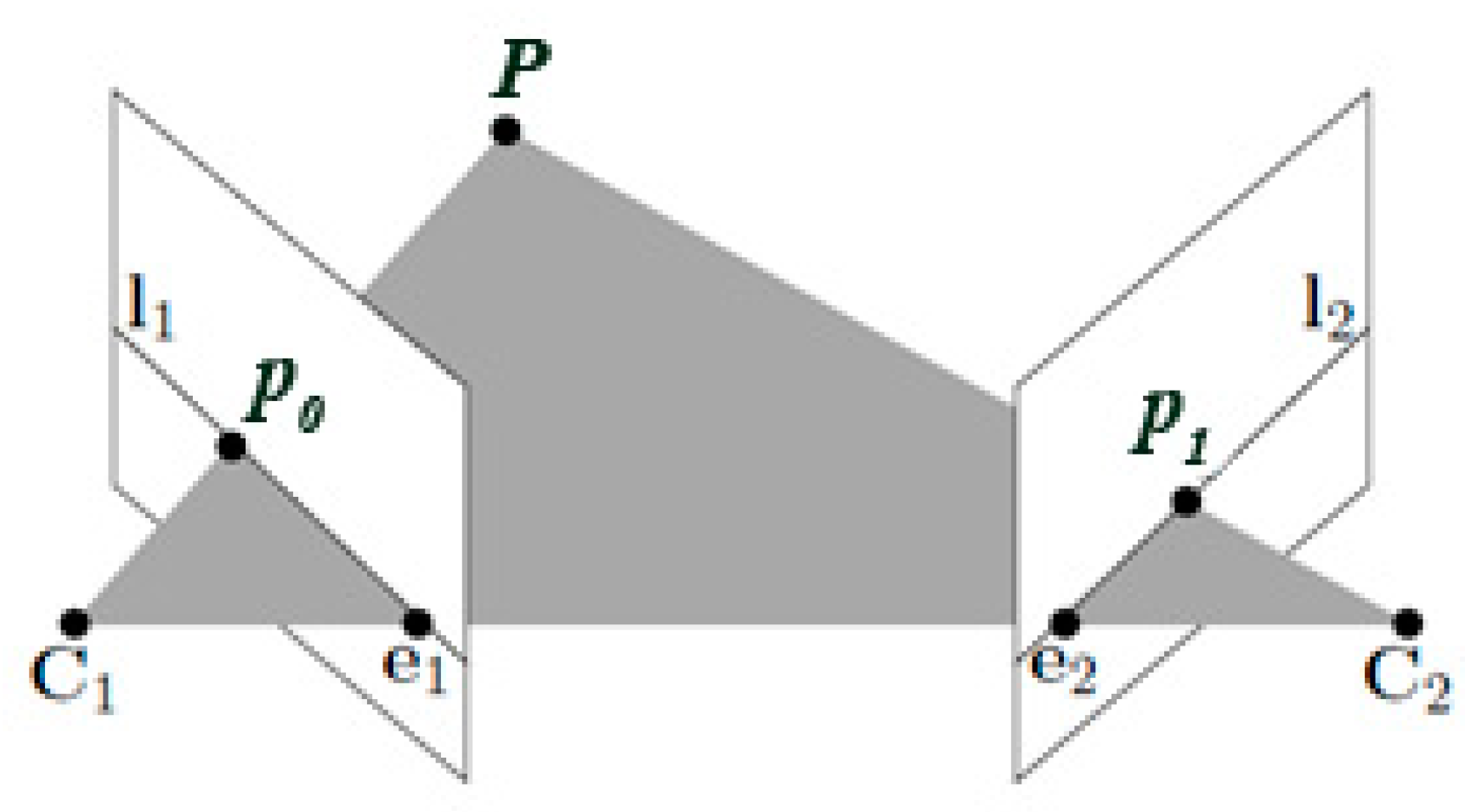
2.2. Imaging Geometry for UAV Oblique Photogrammetry
2.3. Camera Calibration
Camera Calibration—A Mathematical Model
- calibrated focal length—ck;
- the projection centers in relation to the pictures, determined by x0 and y0—image coordinates of the principal point;
- lens distortion: radial (k1, k2, k3) and decentering (p1 and p2) lens distortion coefficients.
2.4. Relative Orientation
2.5. Rectify Action Camera Images
3. Research
3.1. Study Site and Data Set
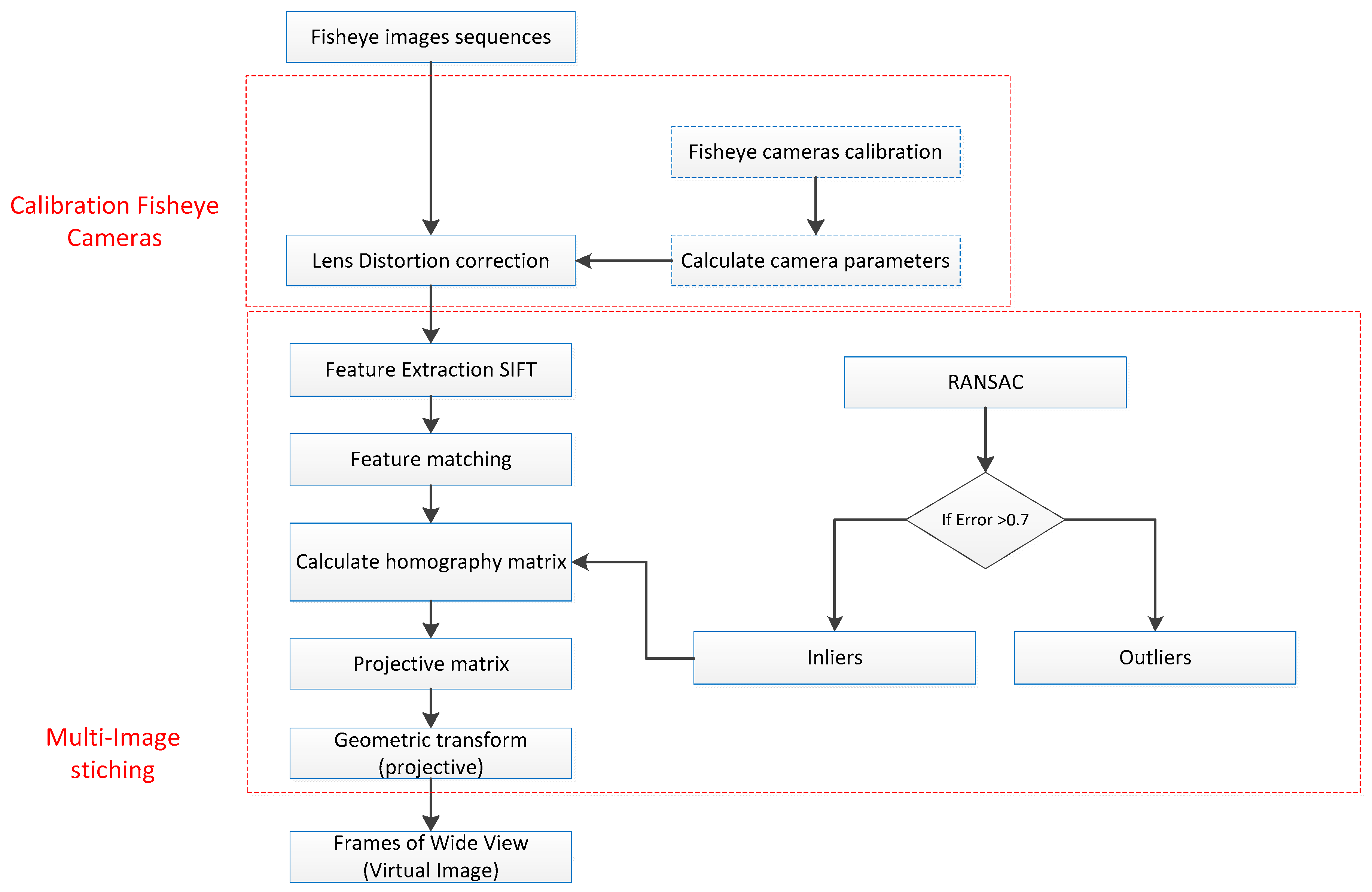
3.2. Proposed Approach
- (a)
- Acquiring low-level images with cameras with the fish-eye lens;
- (b)
- Calibration of cameras;
- (c)
- Geometric correction of images due to distortion (Lens distortion correction);
- (d)
- Relative orientation based on the SIFT and FLANN matcher descriptor;
- (e)
- Projective transformation (Geometric Transform)
- (f)
- Mosaicking to generate one large image.
4. Results
4.1. Results of Camera Calibration
4.2. Undistorted Fisheye Video Sequence
4.3. Visual Evaluation of the Undistortion Method
4.4. Relative Orientation—Feature Image Matching
- (a)
- Torsional factor in homography (H3.1, H3.2) cannot be too significant. Its absolute value is usually less than 0.002.
- (b)
- A shift between images is not allowed when combining images. The homography is rejected if it changes the x and y coordinate between itself.
5. Accuracy Assessment of Rectifying Results
5.1. Results from Multi-Camera Matching
5.2. Result of Image Stitching
6. Discussion
7. Conclusions
Funding
Conflicts of Interest
References
- Remondino, F.; Gerke, M. Oblique Aerial Imagery—A Review. In Proceedings of the Photogrammetric Week 2015, Stuttgart, Germany, 7–11 September 2015; pp. 75–83. [Google Scholar]
- Jiang, S.; Jiang, W. On-board GNSS/IMU assisted feature extraction and matching for oblique UAV images. Remote Sens. 2017, 9, 813. [Google Scholar] [CrossRef]
- Sun, Y.; Sun, H.; Yan, L.; Fan, S.; Chen, R. RBA: Reduced Bundle Adjustment for oblique aerial photogrammetry. ISPRS J. Photogramm. Remote Sens. 2016, 121, 128–142. [Google Scholar] [CrossRef]
- Gruber, M.; Ladstädter, R. Results from ultracam monolithic stitching. In Proceedings of the ASPRS Annual Conference, Milwaukee, WI, USA, 1–5 May 2011; pp. 1–6. [Google Scholar]
- Zeitler, W.; Doerstel, C.; Jacobsen, K. Geometric Calibration of the DMC: Method and Results. ISPRS J. Photogramm. Remote Sens. 2002, 34, 324–332. [Google Scholar]
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef]
- Gonçalves, J.A.; Henriques, R. UAV photogrammetry for topographic monitoring of coastal areas. ISPRS J. Photogramm. Remote Sens. 2015, 104, 101–111. [Google Scholar] [CrossRef]
- Burdziakowski, P.; Bobkowska, K. Accuracy of a low-cost autonomous hexacopter platforms navigation module for a photogrammetric and environmental measurements. In Proceedings of the Environmental Engineering 10th International Conference, Vilnius, Lithuania, 27–28 April 2017. [Google Scholar]
- Nex, F.; Remondino, F. UAV for 3D mapping applications: A review. Appl. Geomat. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Xiao, J.; Gerke, M.; Vosselman, G. Building extraction from oblique airborne imagery based on robust façade detection. ISPRS J. Photogramm. Remote Sens. 2012, 68, 56–68. [Google Scholar] [CrossRef]
- Wierzbicki, D.; Fryskowska, A.; Kędzierski, M.; Wojtkowska, M.; Delis, P. Method of radiometric quality assessment of NIR images acquired with a custom sensor mounted on an unmanned aerial vehicle. J. Appl. Remote Sens. 2018, 12, 015008. [Google Scholar] [CrossRef]
- Haala, N.; Rothermel, M. Dense multiple stereo matching of highly overlapping UAV imagery. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 387–392. [Google Scholar] [CrossRef]
- Niemeyer, F.; Schima, R.; Grenzdörffer, G. Relative and absolute Calibration of a multihead Camera System with oblique and nadir looking Cameras for a UAS. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2013, 2, 287–291. [Google Scholar] [CrossRef]
- Mostafa, M.M.R.; Schwarz, K.-P. A multi-sensor system for airborne image capture and georreferencing. Photogramm. Eng. Remote Sens. 2000, 66, 1417–1423. [Google Scholar]
- Tommaselli, A.M.G.; Galo, M.; de Moraes, M.V.A.; Marcato, J., Jr.; Caldeira, C.R.T.; Lopes, R.F. Generating Virtual Images from Oblique Frames. Remote Sens. 2013, 5, 1875–1893. [Google Scholar] [CrossRef] [Green Version]
- Jhan, J.P.; Li, Y.T.; Rau, J.Y. A modified projective transformation scheme for mosaicking multi-camera imaging system equipped on a large payload fixed-wing UAS. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-3/W2, 87–93. [Google Scholar] [CrossRef]
- Grenzdörffer, G.; Niemeyer, F.; Schmidt, F. Development of Four Vision Camera System for a Micro-UAV. In Proceedings of the XXII ISPRS Congress, Melbourne, Australia, 25 August–1 September 2012; pp. 369–374. [Google Scholar]
- Aicardi, I.; Chiabrando, F.; Grasso, N.; Lingua, A.M.; Noardo, F.; Spanò, A. UAV photogrammetry with oblique images: First analysis on data acquisition and processing. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 835–842. [Google Scholar] [CrossRef]
- Lin, Y.; Jiang, M.; Yao, Y.; Zhang, L.; Lin, J. Use of UAV oblique imaging for the detection of individual trees in residential environments. Urban For. Urban Green. 2015, 14, 404–412. [Google Scholar] [CrossRef]
- Holtkamp, D.J.; Goshtasby, A.A. Precision registration and mosaicking of multicamera images. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3446–3455. [Google Scholar] [CrossRef]
- Ritchie, G.L.; Sullivan, D.G.; Perry, C.D.; Hook, J.E.; Bednarz, C.W. Preparation of a low-cost digital camera system for remote sensing. Appl. Eng. Agric. 2008, 24, 885–894. [Google Scholar] [CrossRef]
- Rau, J.Y.; Jhan, J.P.; Li, Y.T. Development of a large-format uas imaging system with the construction of a one sensor geometry from a multicamera array. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5925–5934. [Google Scholar] [CrossRef]
- Schneider, J.; Läbe, T.; Förstner, W. Incremental real-time bundle adjustment for multi-camera systems with points at infinity. ISPRS Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 1, W2. [Google Scholar] [CrossRef]
- Detchev, I.; Mazaheri, M.; Rondeel, S.; Habib, A. Calibration of multi-camera photogrammetric systems. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, XL-1, 101–108. [Google Scholar] [CrossRef]
- Detchev, I.; Habib, A.; Mazaheri, M.; Melia, A. Long Term Stability Analysis for a Multi-Camera Photogrammetric System. In Proceedings of the 2015 ASPRS Annual Conference, Tampa, FL, USA, 4–8 May 2015. [Google Scholar]
- Brunn, A.; Meyer, T. Calibration of a Multi-Camera Rover. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B5, 445–452. [Google Scholar] [CrossRef]
- Habib, A.; Detchev, I.; Kwak, E. Stability analysis for a multi-camera photogrammetric system. Sensors 2014, 14, 15084–15112. [Google Scholar] [CrossRef] [PubMed]
- Taha, Z.; Tang, Y.R.; Yap, K.C. Development of an onboard system for flight data collection of a small-scale UAV helicopter. Mechatronics 2011, 21, 132–144. [Google Scholar] [CrossRef]
- Novelty RPAS Ogar MK 2. 2017. Available online: http://noveltyrpas.com/ogar-mk2/ (accessed on 25 August 2017).
- Hu, H.; Zhu, Q.; Du, Z.; Zhang, Y.; Ding, Y. Reliable spatial relationship constrained feature point matching of oblique aerial images. Photogramm. Eng. Remote Sens. 2015, 81, 49–58. [Google Scholar] [CrossRef]
- Jiang, S.; Jiang, W.; Huang, W.; Yang, L. UAV-Based Oblique Photogrammetry for Outdoor Data Acquisition and Offsite Visual Inspection of Transmission Line. Remote Sens. 2017, 9, 278. [Google Scholar] [CrossRef]
- Jiang, S.; Jiang, W. Efficient structure from motion for oblique UAV images based on maximal spanning tree expansion. ISPRS J. Photogramm. Remote Sens. 2017, 132, 140–161. [Google Scholar] [CrossRef]
- GoPro 2016. Gopro Hero 4 Black User Manual. Available online: http://cbcdn2.gp-static.com/uploads/product_manual/file/490/UM_H4Black_ENG_REVA_WEB.pdf (accessed on 3 January 2017).
- Zeisl, B.; Georgel, P.F.; Schweiger, F.; Steinbach, E.G.; Navab, N.; Munich, G. Estimation of Location Uncertainty for Scale Invariant Features Points. In Proceedings of the British Machine Vision Conference (BMVC), London, UK, 7–10 September 2009; pp. 1–12. [Google Scholar]
- Habib, A.; Pullivelli, A.; Mitishita, E.; Ghanma, M.; Kim, E.M. Stability analysis of low-cost digital cameras for aerial mapping using different georeferencing techniques. Photogramm. Rec. 2006, 21, 29–43. [Google Scholar] [CrossRef]
- Balletti, C.; Guerra, F.; Tsioukas, V.; Vernier, P. Calibration of action cameras for photogrammetric purposes. Sensors 2014, 14, 17471–17490. [Google Scholar] [CrossRef] [PubMed]
- Remondino, F.; Fraser, C. Digital camera calibration methods: Considerations and comparisons. International Archives of Photogrammetry. Remote Sens. Spat. Inf. Sci. 2006, 36, 266–272. [Google Scholar]
- Hastedt, H.; Luhmann, T. Investigations on the quality of the interior orientation and its impact in object space for UAV photogrammetry. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 321. [Google Scholar] [CrossRef]
- Kedzierski, M.; Fryskowska, A. Precise method of fisheye lens calibration. In Proceedings of the International Society for Photogrammetry and Remote Sensing (ISPRS) Congress, Beijing, China, 3–11 July 2008; pp. 765–768. [Google Scholar]
- Fryer, J.G. Camera calibration. In Close Range. Photogrammetry and Machine Vision; Atkinson, K.B., Ed.; Whittles Publishing: Caithness, UK, 1996; pp. 156–179. [Google Scholar]
- Luhmann, T.; Fraser, C.; Maas, H.G. Sensor modelling and camera calibration for close-range photogrammetry. ISPRS J. Photogramm. Remote Sen. 2016, 115, 37–46. [Google Scholar] [CrossRef]
- Fraser, C.S. Automatic camera calibration in close range photogrammetry. Photogramm. Eng. Remote Sens. 2013, 79, 381–388. [Google Scholar] [CrossRef]
- Tsai, R.Y. An efficient and accurate camera calibration technique for 3D machine vision. In Proceedings of the International Conference on Computer Vision and Pattern Recognition, Miami Beach, FL, USA, 22–26 June 1986; pp. 364–374. [Google Scholar]
- Weng, J.; Cohen, P.; Herniou, M. Camera calibration with distortion models and accuracy evaluation. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 965–980. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef] [Green Version]
- Brown, D.C. Close-range camera calibration. Photogramm. Eng. 1971, 37, 855–866. [Google Scholar]
- Yin, W.S.; Luo, Y.L.; Li, S.Q. Camera calibration based on OpenCV. Comput. Eng. Des. 2007, 28, 197–199. [Google Scholar]
- Wang, Y.M.; Li, Y.; Zheng, J.B. A camera calibration technique based on OpenCV. In Proceedings of the 3rd International Conference on Information Sciences and Interaction Sciences (ICIS), Chengdu, China, 23–25 June 2010; pp. 403–406. [Google Scholar] [CrossRef]
- De la Escalera, A.; Armingol, J.M. Automatic chessboard detection for intrinsic and extrinsic camera parameter calibration. Sensors 2010, 10, 2027–2044. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Douterloigne, K.; Gautama, S.; Philips, W. Fully automatic and robust UAV camera calibration using chessboard patterns. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; Volume 2, pp. 551–554. [Google Scholar]
- Jhan, J.P.; Rau, J.Y.; Huang, C.Y. Band-to-band registration and ortho-rectification of multilens/multispectral imagery: A case study of MiniMCA-12 acquired by a fixed-wing UAS. ISPRS J. Photogramm. Remote Sens. 2016, 114, 66–77. [Google Scholar] [CrossRef]
- Muja, M.; Lowe, D.G. Fast approximate nearest neighbors with automatic algorithm configuration. In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, Lisboa, Portugal, 5–8 February 2009. [Google Scholar]
- Solem, J.E. Programming Computer Vision with Python: Tools and Algorithms for Analyzing Images; O’Reilly Media. Inc.: Sebastopol, CA, USA, 2012. [Google Scholar]
- Hartley, R.I.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004; 655p. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Hartley, R.I. In Defense of the Eight-Point Algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 580–593. [Google Scholar] [CrossRef]
- Seedahmed, G.H. Direct retrieval of exterior orientation parameters using a 2D projective transformation. Photogramm. Rec. 2006, 21, 211–231. [Google Scholar] [CrossRef]
- Remondino, F.; Börlin, N. Photogrammetric calibration of image sequences acquired with a rotating camera. In Proceedings of the ISPRS Working Group V/1, Panoramic Photogrammetry Workshop, Dresden, Germany, 19–22 February 2004; Volume 34. No. 5/W16. [Google Scholar]
- Cho, W.; Schenk, T. Resampling Digital Imagery to Epipolar Geometry. IAPRS Int. Arch. Photogramm. Remote Sens. 1992, 418, 404–408. [Google Scholar]
- Redzuwan, R.; Radzi, N.A.M.; Din, N.M.; Mustafa, I.S. Affine versus projective transformation for SIFT and RANSAC image matching methods. In Proceedings of the International Conference on Signal and Image Processing Applications (ICSIPA), Kuala Lumpur, Malaysia, 19–21 October 2015; pp. 447–451. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Hastedt, H.; Ekkela, T.; Luhmann, T. Evaluation of the Quality of Action Cameras with Wide-Angle Lenses in UAV Photogrammetry. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B1, 851–859. [Google Scholar] [CrossRef]
- Scaramuzza, D.; Martinelli, A.; Siegwart, R. A toolbox for easily calibrating omnidirectional cameras. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 5695–5701. [Google Scholar]
- Zhao, J.; Zhou, H.J.; Men, G.Z. A method of sift feature points matching for image mosaic. In Proceedings of the International Conference on Machine Learning and Cybernetics, Hebei, China, 12–15 July 2009; Volume 4, pp. 2353–2357. [Google Scholar] [CrossRef]
- Brown, M.; Lowe, D.G. Automatic panoramic image stitching using invariant features. Int. J. Comput. Vis. 2007, 74, 59–73. [Google Scholar] [CrossRef]
- Wang, C.; Liu, X.; Zhao, X.; Wang, Y. An Effective Correction Method for Seriously Oblique Remote Sensing Images Based on Multi-View Simulation and a Piecewise Model. Sensors 2016, 16, 1725. [Google Scholar] [CrossRef] [PubMed]
- Pan, X.; Zhao, X.; Gao, D.; Li, X. A multi-core parallel mosaic alorithm for multi-view UAV images. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 845–850. [Google Scholar] [CrossRef]








| Item | Description |
|---|---|
| Size [mm] | 41 × 59 × 30 |
| Weight [g] | 88 |
| Optical sensors type | CMOS |
| Digital Video Format | H.264 |
| Nominal focal length [mm] | 3 |
| Image Recording Format | JPEG |
| Max Video Resolution | 3840 × 2160 |
| Effective Photo Resolution | 12.0 MP |
| Sensor size [mm] | 6.16 × 4.62 |
| Pixel pitch [µm] | 1.55 |
| Sensor width [mm] | 4.19 |
| Sensor height [mm] | 2.36 |
| Flight Height [m] | GSD [m] | HFOV Nadir [m] | VFOV Nadir [m] |
|---|---|---|---|
| 50 | 0.029 | 77.61 | 43.63 |
| 75 | 0.043 | 116.42 | 65.44 |
| 100 | 0.057 | 155.23 | 87.26 |
| 125 | 0.072 | 194.04 | 109.07 |
| 150 | 0.086 | 232.84 | 130.89 |
| 175 | 0.100 | 271.65 | 152.70 |
| 200 | 0.115 | 310.46 | 174.52 |
| Parameter | CAM 1 | CAM 2 | CAM 3 | CAM 4 | CAM 5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean Value | σ | Mean Value | σ | Mean Value | σ | Mean Value | σ | Mean Value | σ | |
| ck [mm] | 2.70 | 0.015 | 2.70 | 0.001 | 2.77 | 0.025 | 2.72 | 0.041 | 2.79 | 0.019 |
| x0 [mm] | 0.144 | 0.074 | 0.150 | 0.003 | 0.145 | 0.050 | 0.130 | 0.041 | −0.297 | 0.008 |
| y0 [mm] | −0.056 | 0.007 | 0.024 | 0.005 | 0.096 | 0.051 | 0.069 | 0.076 | 0.025 | 0.107 |
| k1 | 4.56 × 10−4 | 2.31 × 10−6 | 4.59 × 10−4 | 3.72 × 10−8 | 4.62 × 10−4 | 2.26 × 10−6 | 4.61 × 10−4 | 1.36 × 10−6 | 4.56 × 10−4 | 1.42 × 10−6 |
| k2 | 2.70 × 10−7 | 1.87 × 10−8 | 2.89 × 10−7 | 9.72 × 10−10 | 2.65 × 10−7 | 1.98 × 10−8 | 2.57 × 10−7 | 1.21 × 10−8 | 2.80 × 10−7 | 1.18 × 10−8 |
| k3 | 3.86 × 10−11 | 3.98 × 10−11 | 1.75 × 10−11 | 2.73 × 10−12 | 3.10 × 10−11 | 4.88 × 10−11 | 1.06 × 10−10 | 2.85 × 10−11 | 3.51 × 10−11 | 2.60 × 10−11 |
| k4 | −3.27 × 10−2 | 2.72 × 10−3 | −9.10 × 10−2 | 3.12 × 10−3 | −1.99 × 10−2 | 1.09 × 10−3 | −1.17 × 10−2 | 2.93 × 10−3 | −8.30 × 10−2 | 1.32 × 10−3 |
| p1 | 6.00 × 10−5 | 3.49 × 10−5 | −3.46 × 10−5 | 1.00 × 10−6 | 9.87 × 10−5 | 3.29 × 10−5 | 2.91 × 10−5 | 2.44 × 10−5 | 5.68 × 10−5 | 1.30 × 10−5 |
| p2 | 3.46 × 10−6 | 4.85 × 10−6 | −6.34 × 10−5 | 2.54 × 10−6 | −3.42 × 10−4 | 3.09 × 10−5 | 6.04 × 10−5 | 5.00 × 10−5 | −1.85 × 10−4 | 6.49 × 10−5 |
| Reprojection error [pix] | 0.29 | 0.24 | 0.16 | 0.34 | 0.26 | 0.29 | 0.24 | 0.16 | 0.34 | 0.26 |
| Stereograms | Cam1 and Cam2 | Cam2 and Cam3 | Cam3 and Cam4 | Cam4 and Cam5 |
|---|---|---|---|---|
| Raw matches | 2497 | 3397 | 3246 | 4319 |
| Cameras | Inliers (RANSAC) | Fundamental Matrix Error |
|---|---|---|
| Cam1 and Cam2 | 249 | −0.002334 |
| Cam2 and Cam3 | 332 | −0.000219 |
| Cam3 and Cam4 | 380 | 0.000074 |
| Cam4 and Cam5 | 682 | 0.032159 |
| Image Pairs | RMSEx [pix] | RMSEy [pix] | Total RMSExy [pix] |
|---|---|---|---|
| Cam1 and Cam2 | 1.67 | 1.32 | 2.13 |
| Cam2 and Cam3 | 2.48 | 2.88 | 3.80 |
| Cam3 and Cam4 | 2.59 | 2.09 | 3.32 |
| Cam4 and Cam5 | 2.58 | 2.28 | 3.45 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wierzbicki, D. Multi-Camera Imaging System for UAV Photogrammetry. Sensors 2018, 18, 2433. https://doi.org/10.3390/s18082433
Wierzbicki D. Multi-Camera Imaging System for UAV Photogrammetry. Sensors. 2018; 18(8):2433. https://doi.org/10.3390/s18082433
Chicago/Turabian StyleWierzbicki, Damian. 2018. "Multi-Camera Imaging System for UAV Photogrammetry" Sensors 18, no. 8: 2433. https://doi.org/10.3390/s18082433
APA StyleWierzbicki, D. (2018). Multi-Camera Imaging System for UAV Photogrammetry. Sensors, 18(8), 2433. https://doi.org/10.3390/s18082433





