Fibre Bragg Grating Based Strain Sensors: Review of Technology and Applications
Abstract
:1. Introduction
2. Optical Fibre Devices for Strain Sensing
3. Key FBG Performance Factors of the Fibre-Optic Sensors
4. Physics of Fibre Bragg Grating
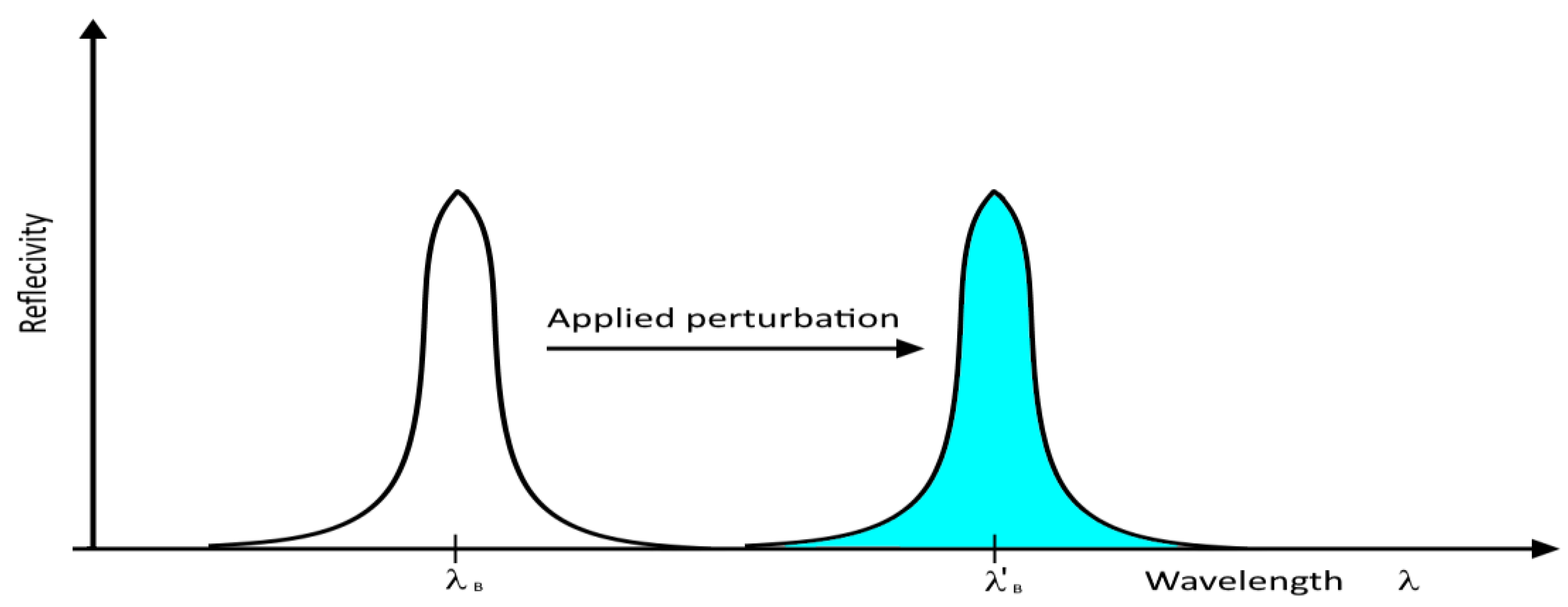
5. Operation Principle of Strain Sensors Based on Fibre Bragg Grating
6. Operation Principle of Splitting Mode Strain Sensors Based on Bragg Grating Ring Resonators
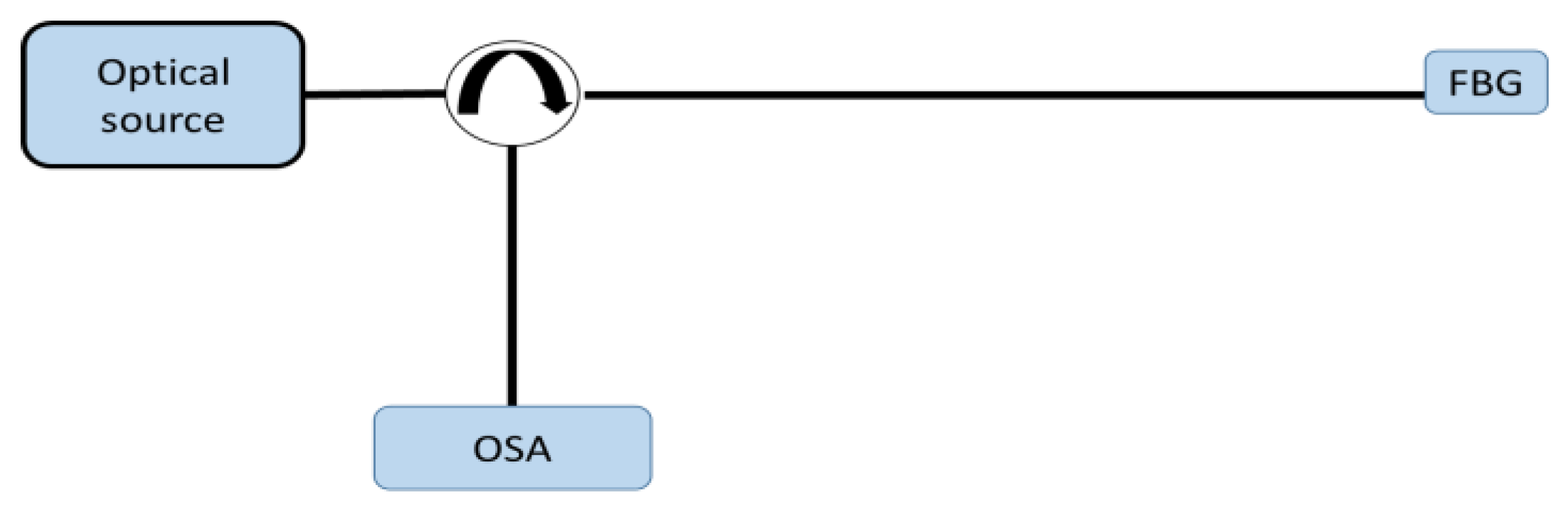
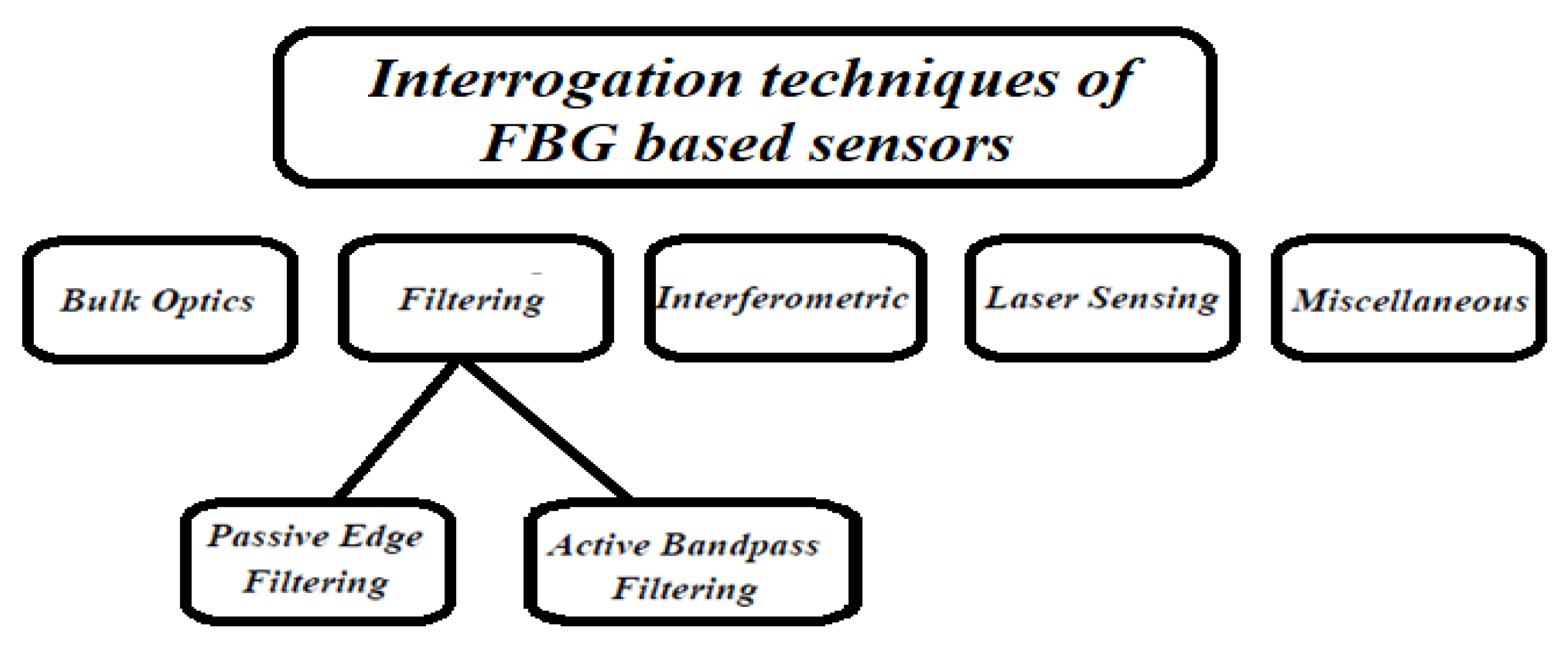
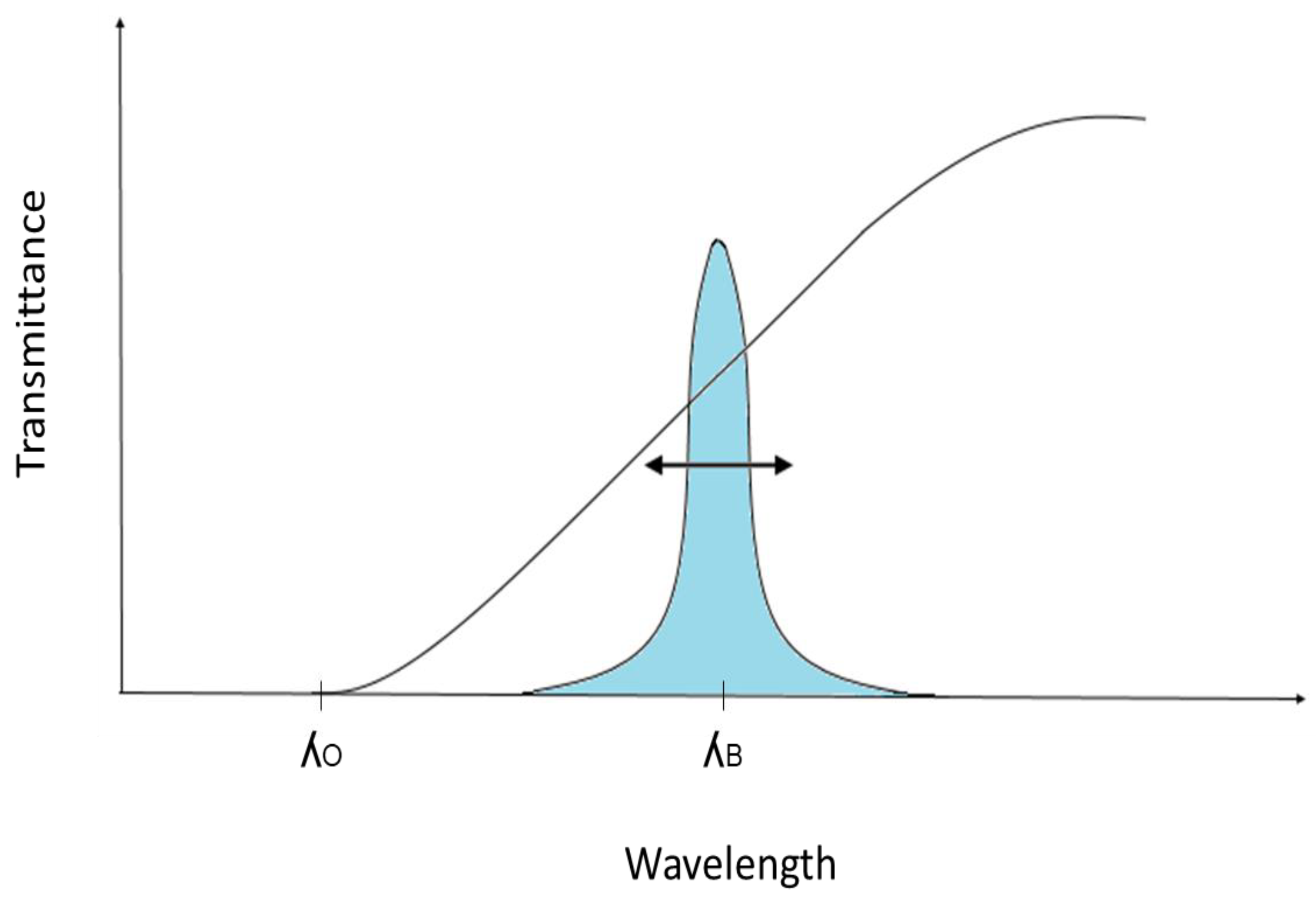
7. FBG Strain Sensors Interrogation Techniques
8. Performance Evaluation of the Strain Sensors
9. Key Sectors and Main Market Players Composing the Global FBG Strain Sensors Market
10. Conclusions
Author Contributions
Conflicts of Interest
References
- Yu, F.T.S.; Yin, S. Fiber Optic Sensors; Marcel Dekker Ltd.: New York, NY, USA, 2002. [Google Scholar]
- Yin, S.; Ruffin, P.; Yu, F. Fiber Optic Sensors, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Gupta, B.D. Fiber Optic Sensors; New India Publishing Agency (NIPA): New Delhi, India, 2006. [Google Scholar]
- Udd, E.; Spillman, W. Fiber Optic Sensors: An Introduction for Engineers and Scientists; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Marcus, M.A. Fiber Optic Sensor Technology and Applications IV. In Proceedings SPIE Conference; SPIE: Bellingham, WA, USA, 2005. [Google Scholar]
- Lubliner, J. Plasticity Theory (Dover Books on Engineering); Dover Publications: New York, NY, USA, 2008. [Google Scholar]
- Rees, D. Basic Engineering Plasticity: An Introduction with Engineering and Manufacturing Applications; Butterworth Heinemann: Oxford, UK, 2006. [Google Scholar]
- Gagliardi, G.; Salza, M.; Avino, S.; Ferraro, P.; Natale, P.D. Probing the Ultimate Limit of Fiber-Optic Strain Sensing. Science 2010, 330, 1081–1084. [Google Scholar] [CrossRef] [PubMed]
- Albert, A.C.A.C.J. Fiber Bragg Grating Sensors: Recent Advancements, Industrial Applications and Market Exploitation; Bentham Science Publishers: Emirate of Sharjah, UAE, 2013. [Google Scholar]
- Thévenaz, L. Review and Progress on Distributed Fibre Sensing. Opt. Fiber Sens. 2006, ThC1. [Google Scholar] [CrossRef]
- Campanella, C.E.; Ai, G.; Ukil, A. Distributed fiber optics techniques for gas network monitoring. In Proceedings of the 2016 IEEE International Conference on Industrial Technology (ICIT), Taipei, Taiwan, 14–17 March 2016; pp. 646–651. [Google Scholar]
- Cieszczyk, S.; Kisaa, P. Inverse problem of determining periodic surface profile oscillation defects of steel materials with a fiber Bragg grating sensor. Appl. Opt. 2016, 55, 1412. [Google Scholar] [CrossRef] [PubMed]
- Barrias, A.; Casas, J.; Villalba, S. A Review of Distributed Optical Fiber Sensors for Civil Engineering Applications. Sensors 2016, 16, 748. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, X.; Zhang, Z.; Li, L. Wind direction sensing system based on fiber Bragg grating sensor. Appl. Opt. 2017, 56, 9862. [Google Scholar] [CrossRef]
- Zheng, S.; Zhang, N.; Xia, Y.; Wang, H. Research on non-uniform strain profile reconstruction along fiber Bragg grating via genetic programming algorithm and interrelated experimental verification. Opt. Commun. 2014, 315, 338–346. [Google Scholar] [CrossRef]
- Mihailov, S.J. Fiber Bragg Grating Sensors for Harsh Environments. Sensors 2012, 12, 1898–1918. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Joe, H.E.; Yun, H.; Jo, S.H.; Jun, M.B.; Min, B.K. A review on optical fiber sensors for environmental monitoring. Int. J. Precis. Eng. Manuf. Green Technol. 2018, 5, 173–191. [Google Scholar] [CrossRef]
- Chuang, S.L. Physics of Photonic Devices; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Pierce, J.R. Coupling of Modes of Propagation. J. Appl. Phys. 1954, 25, 179–183. [Google Scholar] [CrossRef]
- Russell, P.S.J.; Archambault, J.L.; Reekie, L. Fibre gratings. Phys. World 1993, 6, 41. [Google Scholar] [CrossRef]
- Khan, S.S.A.; Islam, M.S. Determination of the Best Apodization Function and Grating Length of Linearly Chirped Fiber Bragg Grating for Dispersion Compensation. J. Commun. 2012, 7, 840–846. [Google Scholar] [CrossRef]
- Khare, A.; Singh, J. Design and Study of Chirped Fiber Bragg Grating for Sensing of Hazardous Gases. Int. J. Comput. Appl. 2011, 23, 40–43. [Google Scholar] [CrossRef] [Green Version]
- Huang, W.; Zhang, W.; Zhen, T.; Bian, C.; Du, Y.; Li, F. π-phase-shifted FBG for improving static-strain measurement resolution based on triangle-wave laser tuning technique. In Proceedings of the 23rd International Conference on Optical Fibre Sensors, Santander, Spain, 2–6 June 2014; López-Higuera, J.M., Jones, J.D.C., López-Amo, M., Santos, J.L., Eds.; SPIE: California, FL, USA, 2014. [Google Scholar]
- Liu, Y.; Lee, S.B.; Choi, S.S. Phase-Shifted Fiber Bragg Grating Transmission Filters Based on the Fabry-Perot Effect. J. Opt. Soc. Korea 1998, 2, 30–33. [Google Scholar] [CrossRef] [Green Version]
- Hill, K.; Meltz, G. Fiber Bragg grating technology fundamentals and overview. J. Lightw. Technol. 1997, 15, 1263–1276. [Google Scholar] [CrossRef]
- Campanella, C.E.; Giorgini, A.; Avino, S.; Malara, P.; Zullo, R.; Gagliardi, G.; Natale, P.D. Localized strain sensing with fiber Bragg-grating ring cavities. Opt. Express 2013, 21, 29435. [Google Scholar] [CrossRef] [PubMed]
- Campanella, C. Coupled π-shifted fibre Bragg grating ring resonant strain sensors. Electron. Lett. 2016, 52, 1873–1875. [Google Scholar] [CrossRef]
- Malara, P.; Campanella, C.E.; Giorgini, A.; Avino, S.; Gagliardi, G. Fiber Bragg grating laser sensor with direct radio-frequency readout. Opt. Lett. 2016, 41, 1420. [Google Scholar] [CrossRef] [PubMed]
- Campanella, C.E.; Mastronardi, L.; De Leonardis, F.; Malara, P.; Gagliardi, G.; Passaro, V.M.N. Investigation of fiber Bragg grating based mode-splitting resonant sensors. Opt. Express 2014, 22, 25371. [Google Scholar] [CrossRef] [PubMed]
- Malara, P.; Mastronardi, L.; Campanella, C.E.; Giorgini, A.; Avino, S.; Passaro, V.M.N.; Gagliardi, G. Split-mode fiber Bragg grating sensor for high-resolution static strain measurements. Opt. Lett. 2014, 39, 6899. [Google Scholar] [CrossRef] [PubMed]
- De Leonardis, F.; Campanella, C.; Troia, B.; Perri, A.; Passaro, V. Performance of SOI Bragg Grating Ring Resonator for Nonlinear Sensing Applications. Sensors 2014, 14, 16017–16034. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Campanella, C.M.; Dunai, M.; Calabrese, L.; Campanella, C.E. Design guidelines for nanoparticle chemical sensors based on mode-splitting silicon-on-insulator planar microcavities. J. Opt. Soc. Am. B 2016, 33, 2383. [Google Scholar] [CrossRef]
- Malara, P.; Campanella, C.E.; Giorgini, A.; Avino, S.; Natale, P.D.; Gagliardi, G. Super-Resonant Intracavity Coherent Absorption. Sci. Rep. 2016, 6, 28947. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Campanella, C.E.; Malara, P.; Campanella, C.M.; Giove, F.; Dunai, M.; Passaro, V.M.N.; Gagliardi, G. Mode-splitting cloning in birefringent fiber Bragg grating ring resonators. Opt. Lett. 2016, 41, 2672. [Google Scholar] [CrossRef] [PubMed]
- Campanella, C.E.; De Leonardis, F.; Passaro, V.M.N. Fiber Bragg grating ring resonators under rotation for angular velocity sensing. Appl. Opt. 2015, 54, 4789. [Google Scholar] [CrossRef] [PubMed]
- Campanella, C.E.; De Leonardis, F.; Mastronardi, L.; Malara, P.; Gagliardi, G.; Passaro, V.M.N. Investigation of refractive index sensing based on Fano resonance in fiber Bragg grating ring resonators. Opt. Express 2015, 23, 14301. [Google Scholar] [CrossRef] [PubMed]
- Malara, P.; Campanella, C.E.; De Leonardis, F.; Giorgini, A.; Avino, S.; Passaro, V.M.N.; Gagliardi, G. Enhanced spectral response of -phase shifted fiber Bragg gratings in closed-loop configuration. Opt. Lett. 2015, 40, 2124. [Google Scholar] [CrossRef] [PubMed]
- Campanella, C.E.; Campanella, C.M.; De Leonardis, F.; Passaro, V.M.N. A high efficiency label-free photonic biosensor based on vertically stacked ring resonators. Eur. Phys. J. Spec. Top. 2014, 223, 2009–2021. [Google Scholar] [CrossRef]
- Campanella, C.E.; Carlo, M.D.; Cuccovillo, A.; Passaro, V.M.N. Loss-induced control of light propagation direction in passive linear coupled optical cavities. Photonics Res. 2018, 6, 525. [Google Scholar] [CrossRef]
- Tosi, D. Review and Analysis of Peak Tracking Techniques for Fiber Bragg Grating Sensors. Sensors 2017, 17, 2368. [Google Scholar] [CrossRef] [PubMed]
- Lamberti, A.; Vanlanduit, S.; Pauw, B.D.; Berghmans, F. A novel fast phase correlation algorithm for peak wavelength detection of fiber Bragg grating sensors. Opt. Express 2014, 22, 7099. [Google Scholar] [CrossRef] [PubMed]
- Tosi, D. KLT-Based Algorithm for Sub-Picometer Accurate FBG Tracking With Coarse Wavelength Sampling. IEEE Photonics Technol. Lett. 2015, 27, 2134–2137. [Google Scholar] [CrossRef]
- Melle, S.; Liu, K.; Measures, R. A passive wavelength demodulation system for guided-wave Bragg grating sensors. IEEE Photonics Technol. Lett. 1992, 4, 516–518. [Google Scholar] [CrossRef]
- Cui, J.; Hu, Y.; Feng, K.; Li, J.; Tan, J. FBG Interrogation Method with High Resolution and Response Speed Based on a Reflective-Matched FBG Scheme. Sensors 2015, 15, 16516–16535. [Google Scholar] [CrossRef] [PubMed]
- Cheng, R.; Xia, L.; Ran, Y.; Rohollahnejad, J.; Zhou, J.; Wen, Y. Interrogation of Ultrashort Bragg Grating Sensors Using Shifted Optical Gaussian Filters. IEEE Photonics Technol. Lett. 2015, 27, 1833–1836. [Google Scholar] [CrossRef]
- Zhang, Z.; Yan, L.; Pan, W.; Luo, B.; Wang, P.; Guo, L.; Zhou, W. Sensitivity Enhancement of Strain Sensing Utilizing a Differential Pair of Fiber Bragg Gratings. Sensors 2012, 12, 3891–3900. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kang, S.C. Real-time measurement for static and dynamic strain using a fiber Bragg grating and the ASE profile of EDFA. In Proceedings of the 13th International Conference on Optical Fiber Sensors, Kyongju, Korea, 12–16 April 1999. [Google Scholar]
- Melle, S.M.; Liu, K.; Measures, R.M. Practical fiber-optic Bragg grating strain gauge system. Appl. Opt. 1993, 32, 3601. [Google Scholar] [CrossRef] [PubMed]
- Black, E.D. An introduction to PoundDreverHall laser frequency stabilization. Am. J. Phys. 2001, 69, 79–87. [Google Scholar] [CrossRef]
- Liu, N.; Li, Y.; Wang, Y.; Wang, H.; Liang, W.; Lu, P. Bending insensitive sensors for strain and temperature measurements with Bragg gratings in Bragg fibers. Opt. Express 2011, 19, 13880. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Du, Y.; Liu, C. FBG Strain Sensor Based on Thermal Stress Mechnism. In Proceedings of the 2008 Second International Symposium on Intelligent Information Technology Application, Shanghai, China, 20–22 December 2008; pp. 640–642. [Google Scholar]
- Moscato, M.; Schena, E.; Saccomandi, P.; Francomano, M.; Accoto, D.; Guglielmelli, E.; Silvestri, S. A micromachined intensity-modulated fiber optic sensor for strain measurements: Working principle and static calibration. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; pp. 5790–5793. [Google Scholar]
- Ferreira, M.; Bierlich, J.; Becker, M.; Schuster, K.; Santos, J.; Frazão, O. Ultra-High Sensitive Strain Sensor Based on Post-Processed Optical Fiber Bragg Grating. Fibers 2014, 2, 142–149. [Google Scholar] [CrossRef] [Green Version]
- Bhowmik, K.; Peng, G.D.; Luo, Y.; Ambikairajah, E.; Lovric, V.; Walsh, W.R.; Rajan, G. High Intrinsic Sensitivity Etched Polymer Fiber Bragg Grating Pair for Simultaneous Strain and Temperature Measurements. IEEE Sens. J. 2016, 16, 2453–2459. [Google Scholar] [CrossRef]
- Wang, Y.; Qiao, X.; Yang, H.; Su, D.; Li, L.; Guo, T. Sensitivity-Improved Strain Sensor over a Large Range of Temperatures Using an Etched and Regenerated Fiber Bragg Grating. Sensors 2014, 14, 18575–18582. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yuan, W.; Stefani, A.; Bang, O. Tunable Polymer Fiber Bragg Grating (FBG) Inscription: Fabrication of Dual-FBG Temperature Compensated Polymer Optical Fiber Strain Sensors. IEEE Photonics Technol. Lett. 2012, 24, 401–403. [Google Scholar] [CrossRef] [Green Version]
- Gagliardi, G.; Salza, M.; Ferraro, P.; Natale, P.D. Fiber Bragg-grating strain sensor interrogation using laser radio-frequency modulation. Opt. Express 2005, 13, 2377. [Google Scholar] [CrossRef] [PubMed]
- Du, J.; He, Z. Sensitivity enhanced strain and temperature measurements based on FBG and frequency chirp magnification. Opt. Express 2013, 21, 27111. [Google Scholar] [CrossRef] [PubMed]
- Kuse, N.; Ozawa, A.; Kobayashi, Y. Static FBG strain sensor with high resolution and large dynamic range by dual-comb spectroscopy. Opt. Express 2013, 21, 11141. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Tokunaga, T.; He, Z. Sub-nano resolution fiber-optic static strain sensor using a sideband interrogation technique. Opt. Lett. 2012, 37, 434. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; He, Z.; Tokunaga, T.; Hotate, K. An ultra-high-resolution large-dynamic-range fiber optic static strain sensor using Pound-Drever-Hall technique. In Proceedings of the 2011 International Quantum Electronics Conference (IQEC) and Conference on Lasers and Electro-Optics (CLEO) Pacific Rim Incorporating the Australasian Conference on Optics, Lasers and Spectroscopy and the Australian Conference on Optical Fibre Technology, Sydney, NSW, Australia, 28 August–1 September 2011; pp. 130–132. [Google Scholar]
- Wang, Y.; Cui, Y.; Yun, B. A fiber Bragg grating sensor system for simultaneously static and dynamic measurements with a wavelength-swept fiber laser. IEEE Photonics Technol. Lett. 2006, 18, 1539–1541. [Google Scholar] [CrossRef]
- Lam, T.T.; Chow, J.H.; Shaddock, D.A.; Gray, M.B.; McClelland, D.E. Fiber optic strain sensing using an absolute frequency reference. In Proceedings of the 35th Australian Conference on Optical Fibre Technology, Melbourne, Australia, 5–9 December 2010. [Google Scholar]
- Xu, O.; Zhang, J.; Deng, H.; Yao, J. Dual-frequency Optoelectronic Oscillator for Thermal-Insensitive Interrogation of a FBG Strain Sensor. IEEE Photonics Technol. Lett. 2017, 29, 357–360. [Google Scholar] [CrossRef]
- Yoo, K.W.; Han, Y.G. Sensitivity improvement in fiber Bragg grating sensors using all-fiber weak value amplification based on optical attenuation. J. Lightw. Technol. 2017, 36, 968–973. [Google Scholar] [CrossRef]
- Chen, J.; Liu, Q.; He, Z. High-Resolution Simultaneous Measurement of Strain and Temperature Using pi-Phase-Shifted FBG in Polarization Maintaining Fiber. J. Lightw. Technol. 2017, 35, 4838–4844. [Google Scholar] [CrossRef]
- Liu, J.; Wang, M.; Tang, Y.; Yang, Y.; Wu, Y.; Jin, W.; Jian, S. Switchable Optoelectronic Oscillator Using an FM-PS-FBG for Strain and Temperature Sensing. IEEE Photonics Technol. Lett. 2017, 29, 2008–2011. [Google Scholar] [CrossRef]
- Maheshwari, M.; Tjin, S.C.; Yang, Y.; Asundi, A. Wavelength-shifted chirped FBGs for temperature compensated strain measurement. Sens. Actuators A 2017, 265, 231–235. [Google Scholar] [CrossRef]
- Wen, H.; Terrel, M.; Fan, S.; Digonnet, M. Sensing With Slow Light in Fiber Bragg Gratings. IEEE Sens. J. 2012, 12, 156–163. [Google Scholar] [CrossRef]
- Wen, H.; Skolianos, G.; Fan, S.; Bernier, M.; Vallee, R.; Digonnet, M.J.F. Slow-Light Fiber-Bragg-Grating Strain Sensor With a 280 femtostrain/Hz Resolution. J. Lightw. Technol. 2013, 31, 1804–1808. [Google Scholar] [CrossRef]
- Gagliardi, G.; Nicola, S.D.; Ferraro, P.; Natale, P.D. Interrogation of fiber Bragg-grating resonators by polarization-spectroscopy laser-frequency locking. Opt. Express 2007, 15, 3715. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Han, Y.G.; Chang, Y.; Lee, S. Raman amplifier based long-distance, remote FBG strain sensor with EDF broadband source recycling residual Raman pump. Electron. Lett. 2004, 40, 1106. [Google Scholar] [CrossRef]
- He, Z.; Liu, Q.; Tokunaga, T. Ultrahigh resolution fiber-optic quasi-static strain sensors for geophysical research. Photonic Sens. 2013, 3, 295–303. [Google Scholar] [CrossRef]
- He, Z.; Liu, Q.; Tokunaga, T. Development of nano-strain-resolution fiber optic static strain sensor for crustal deformation monitoring. In Proceedings of the 2012 Asia Communications and Photonics Conference (ACP), Guangzhou, China, 7–10 November 2012; pp. 1–3. [Google Scholar]
- Zhang, H.; Wang, Q.; Wang, H.; Song, S.; Zhao, B.; Dai, Y.; Huang, G.; Jiang, Z. Fiber Bragg Grating Sensor for Strain Sensing in Low Temperature Superconducting Magnet. IEEE Trans. Appl. Supercond. 2010, 20, 1798–1801. [Google Scholar] [CrossRef]
- Qingmin, H.; Wenling, J.; Shuhui, Z.; Liang, R.; Ziguang, J. Natural Gas Pipeline Leakage Detection Based on FBG Strain Sensor. In Proceedings of the 2013 Fifth International Conference on Measuring Technology and Mechatronics Automation, Hong Kong, China, 16–17 January 2013; pp. 712–715. [Google Scholar]
- Han, B.; Li, L.; Wu, Z.; Jing, H. Applications of FBG and ZigBee in telemetering of vortex-induced vibration for pipelines. In Proceedings of the 2013 22nd Wireless and Optical Communication Conference, Chongqing, China, 16–18 May 2013; pp. 595–600. [Google Scholar]
- Wang, J.; Zhao, L.; Liu, T.; Li, Z.; Sun, T.; Grattan, K.T.V. Novel Negative Pressure Wave-Based Pipeline Leak Detection System Using Fiber Bragg Grating-Based Pressure Sensors. J. Lightw. Technol. 2017, 35, 3366–3373. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Huang, W.; Li, L.; Liu, W.; Li, F. High resolution FBG sensor and its applications in Geophysics. In Proceedings of the 2017 16th International Conference on Optical Communications and Networks (ICOCN), Wuzhen, China, 7–10 August 2017; pp. 1–3. [Google Scholar]
- Hu, B.; Song, G.; Zhang, H.; Liu, T. A precision edge filter interrogation system for mine Fiber Bragg Grating micro-seismic sensors. In Proceedings of the 2017 16th International Conference on Optical Communications and Networks (ICOCN), Wuzhen, China, 7–10 August 2017; pp. 1–3. [Google Scholar]
- Kamikawachi, R.C.; Abe, I.; Kalinowski, H.J.; Fabris, J.L.; Pinto, J.L. Thermal characterization of etched FBG for applications in oil and gas sector. In Proceedings of the 2007 SBMO/IEEE MTT-S International Microwave and Optoelectronics Conference, Brazil, Brazil, 29 Octomber–1 November 2007. [Google Scholar]
- Kim, C.H.; Paek, I.; Yoo, N. Monitoring of small wind turbine blade using FBG sensors. In Proceedings of the 2010 International Conference on Control, Automation and Systems (ICCAS 2010), Gyeonggi-do, Korea, 27 October 2010; pp. 1059–1061. [Google Scholar]
- Bremer, K.; Lewis, E.; Leen, G.; Moss, B.; Lochmann, S.; Mueller, I.; Reinsch, T.; Schroetter, J. Fibre optic pressure and temperature sensor for geothermal wells. In Proceedings of the 2010 IEEE Sensors, Kona, HI, USA, 1–4 November 2010; pp. 538–541. [Google Scholar]
- Huang, Q.; Zhang, C.; Liu, Q.; Ning, Y.; Cao, Y. New type of fiber optic sensor network for smart grid interface of transmission system. In Proceedings of the IEEE PES General Meeting, Providence, RI, USA, 25–29 July 2010. [Google Scholar]
- Campopiano, S.; Cutolo, A.; Cusano, A.; Giordano, M.; Parente, G.; Lanza, G.; Laudati, A. Underwater Acoustic Sensors Based on Fiber Bragg Gratings. Sensors 2009, 9, 4446–4454. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, W.; Li, F.; Liu, Y.; Xiao, H. FBG hydrophone: Theory and experiment. In Proceedings of the 2008 1st Asia-Pacific Optical Fiber Sensors Conference, Chengdu, China, 7–9 November 2008. [Google Scholar]
- Wang, G.; Pran, K.; Sagvolden, G.; Havsgård, G.B.; Jensen, A.E.; Johnson, G.A.; Vohra, S.T. Ship hull structure monitoring using fibre optic sensors. Smart Mater. Struct. 2001, 10, 472–478. [Google Scholar] [CrossRef]
- Allwood, G.; Wild, G.; Hinckley, S. Fiber Bragg Grating Sensors for Mainstream Industrial Processes. Electronics 2017, 6, 92. [Google Scholar] [CrossRef]
- Zhou, Z. Intelligent monitoring technology for machine tools based on FBG sensing. In Proceedings of the 2014 International Conference on Innovative Design and Manufacturing (ICIDM), Montreal, QC, Canada, 13–15 August 2014. [Google Scholar]
- Pei, H.; Cui, P.; Yin, J.; Zhu, H.; Chen, X.; Pei, L.; Xu, D. Monitoring and warning of landslides and debris flows using an optical fiber sensor technology. J. Mt. Sci. 2011, 8, 728–738. [Google Scholar] [CrossRef]
- Allwood, G.; Hinckley, S.; Wild, G. Optical Fiber Bragg grating based intrusion detection systems for homeland security. In Proceedings of the 2013 IEEE Sensors Applications Symposium Proceedings, Galveston, TX, USA, 19–21 February 2013. [Google Scholar]
- Catalano, A.; Bruno, F.; Pisco, M.; Cutolo, A.; Cusano, A. An Intrusion Detection System for the Protection of Railway Assets Using Fiber Bragg Grating Sensors. Sensors 2014, 14, 18268–18285. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boersma, A.; Cremers, R.; Jansen, R. Fiber Bragg Grating Distributed Chemical Sensors. Procedia Eng. 2016, 168, 1245–1248. [Google Scholar] [CrossRef]
- Dziuda, L.; Krej, M.; Skibniewski, F.W. Fiber Bragg Grating Strain Sensor Incorporated to Monitor Patient Vital Signs During MRI. IEEE Sens. J. 2013, 13, 4986–4991. [Google Scholar] [CrossRef] [Green Version]
- Witt, J.; Narbonneau, F.; Schukar, M.; Krebber, K.; Jonckheere, J.D.; Jeanne, M.; Kinet, D.; Paquet, B.; Depre, A.; DAngelo, L.T.; et al. Medical Textiles With Embedded Fiber Optic Sensors for Monitoring of Respiratory Movement. IEEE Sens. J. 2012, 12, 246–254. [Google Scholar] [CrossRef]
- Lee, J.R.; Ryu, C.Y.; Koo, B.Y.; Kang, S.G.; Hong, C.S.; Kim, C.G. In-flight health monitoring of a subscale wing using a fiber Bragg grating sensor system. Smart Mater. Struct. 2003, 12, 147–155. [Google Scholar] [CrossRef]
- Sante, R.D. Fibre Optic Sensors for Structural Health Monitoring of Aircraft Composite Structures: Recent Advances and Applications. Sensors 2015, 15, 18666–18713. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Filograno, M.L.; Guillen, P.C.; Rodriguez-Barrios, A.; Martin-Lopez, S.; Rodriguez-Plaza, M.; Andres-Alguacil, Á.; Gonzalez-Herraez, M. Real-Time Monitoring of Railway Traffic Using Fiber Bragg Grating Sensors. IEEE Sens. J. 2012, 12, 85–92. [Google Scholar] [CrossRef] [Green Version]
- Mennella, F.; Laudati, A.; Esposito, M.; Cusano, A.; Cutolo, A.; Giordano, M.; Campopiano, S.; Breglio, G. Railway monitoring and train tracking by fiber Bragg grating sensors. In Proceedings of the Third European Workshop on Optical Fibre Sensors, Napoli, Italy, 4–6 July 2007. [Google Scholar]
- 3M Science Applied to Life. Available online: https://www.3m.com/ (accessed on 20 December 2017).
- Advanced Optical Solutions GmbH. Available online: www.aos-fibre.com (accessed on 20 December 2017).
- AFW Technologies Pty Ltd. Available online: www.afwtechnologies.com.au (accessed on 20 December 2017).
- Alcatel Optronics. Available online: http://www.alcatel.com/telecom/optronics/ (accessed on 20 December 2017).
- Alxenses Company Ltd. Available online: www.alxenses.com (accessed on 20 December 2017).
- Ascentta Inc. Available online: www.ascentta.com (accessed on 20 December 2017).
- AtGrating (China). Available online: http://www.atgrating.com/en/ (accessed on 20 December 2017).
- Broptics Technology Inc. Available online: www.broptics.com (accessed on 20 December 2017).
- DK Photonics Technology Co., Ltd. Available online: www.dkphotonics.com (accessed on 20 December 2017).
- FBG TECH. Available online: www.fbg.co.kr/eng (accessed on 20 December 2017).
- FBGS International NV. Available online: www.fbgs.com (accessed on 20 December 2017).
- Fibreguide Industries. Available online: www.fibreguide.com (accessed on 20 December 2017).
- Gould Fibre Optic. Available online: https://gouldfo.com/ (accessed on 20 December 2017).
- HBM FibreSensing, S.A. Available online: https://www.hbm.com/fs (accessed on 20 December 2017).
- InPhoTech. Available online: www.inphotech.eu (accessed on 20 December 2017).
- ITF Technologies Inc. Available online: www.itftechnologies.com (accessed on 20 December 2017).
- IXBlue. Available online: www.photonics.ixblue.com (accessed on 20 December 2017).
- Keysight. Available online: www.keysight.com/ (accessed on 20 December 2017).
- MPB Communications. Available online: mpbcommunications.com (accessed on 20 December 2017).
- Optoadvance S.r.l. Available online: http://www.optoadvance.com/ (accessed on 20 December 2017).
- Optromix Co. Available online: www.optromix.com (accessed on 20 December 2017).
- Oxford Lasers Inc. Available online: https://www.oxfordlasers.com/ (accessed on 20 December 2017).
- OZ Optics Limited. Available online: http://www.ozoptics.com/ (accessed on 20 December 2017).
- Proximion AB. Available online: www.proximion.com (accessed on 20 December 2017).
- Technica Optical Components, LLC. Available online: www.technicasa.com (accessed on 20 December 2017).
- TeraXion. Available online: www.teraxion.com (accessed on 20 December 2017).
- Thorlabs Inc. Available online: https://www.thorlabs.com/ (accessed on 20 December 2017).
- VFIBRE Ltd. Available online: www.vfibre.com (accessed on 20 December 2017).




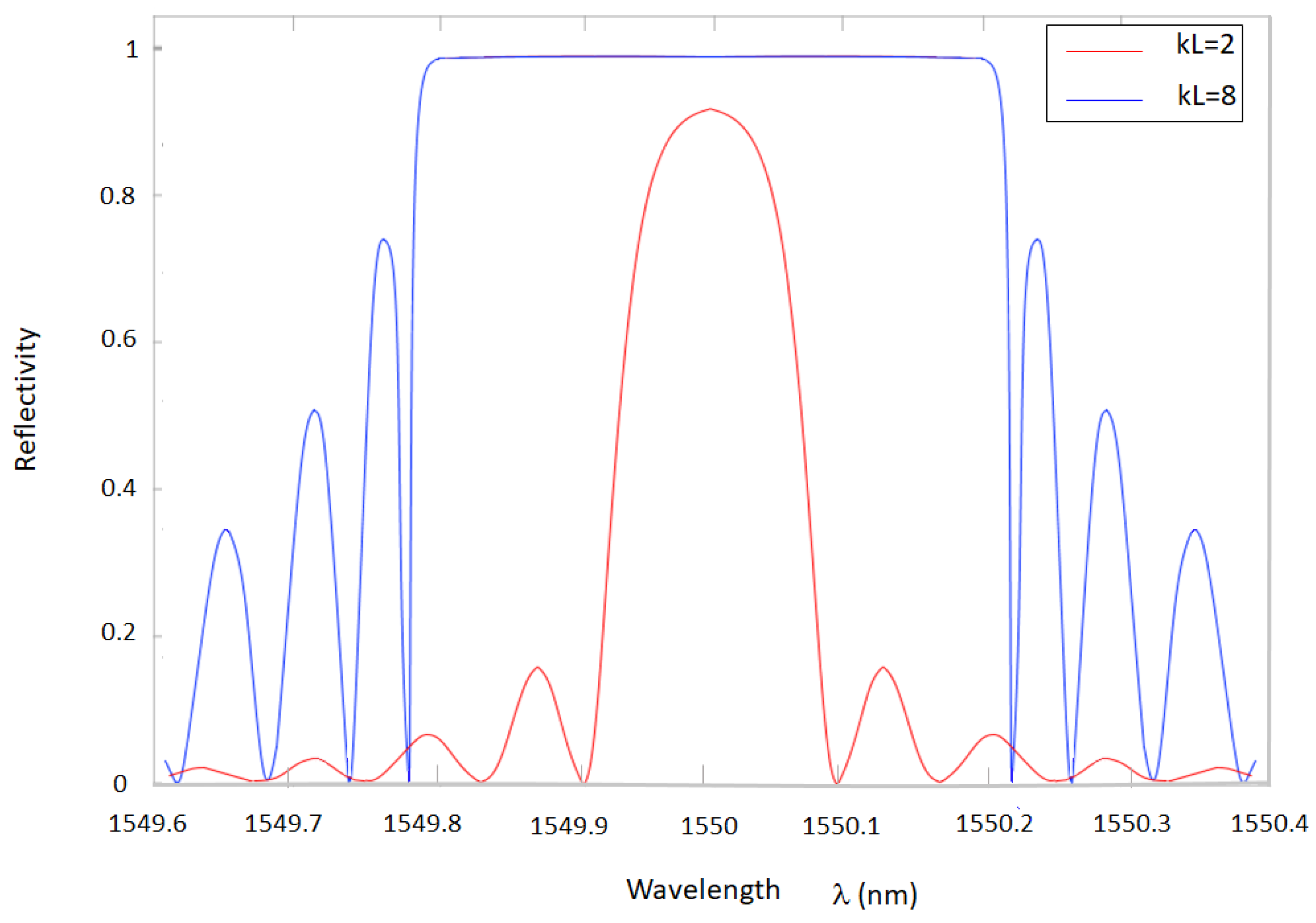
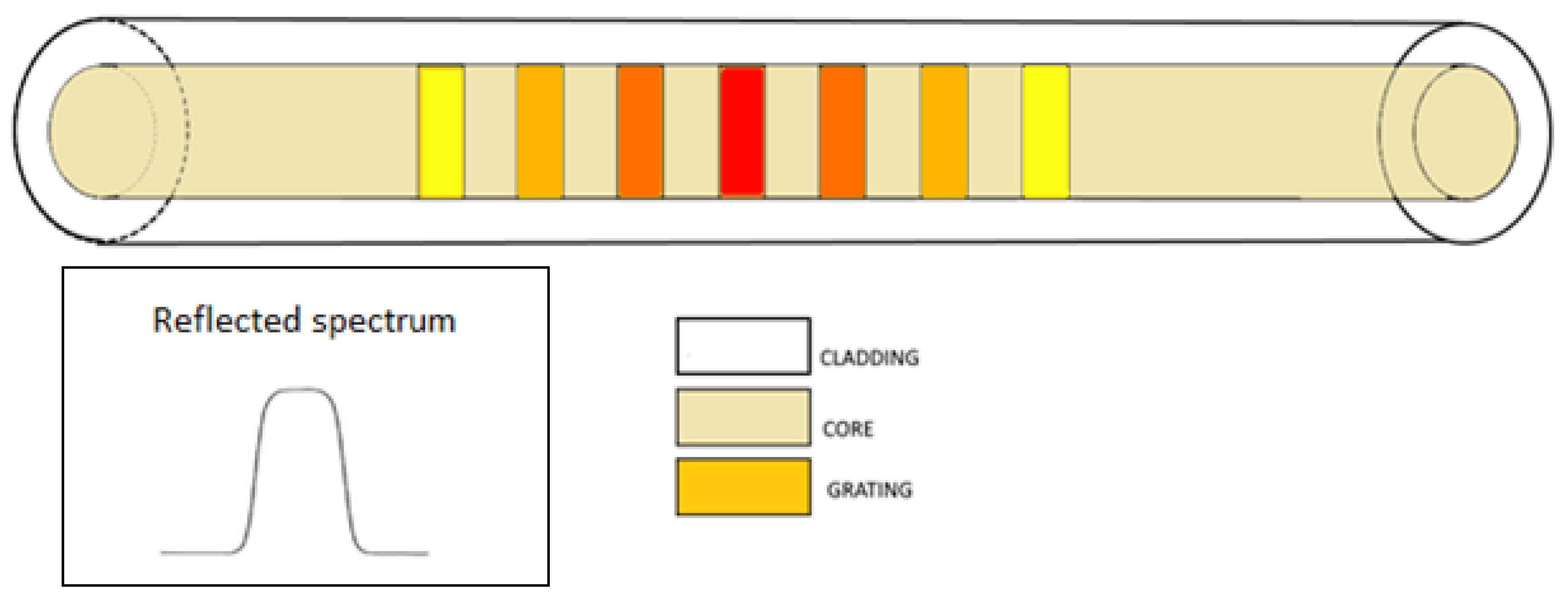
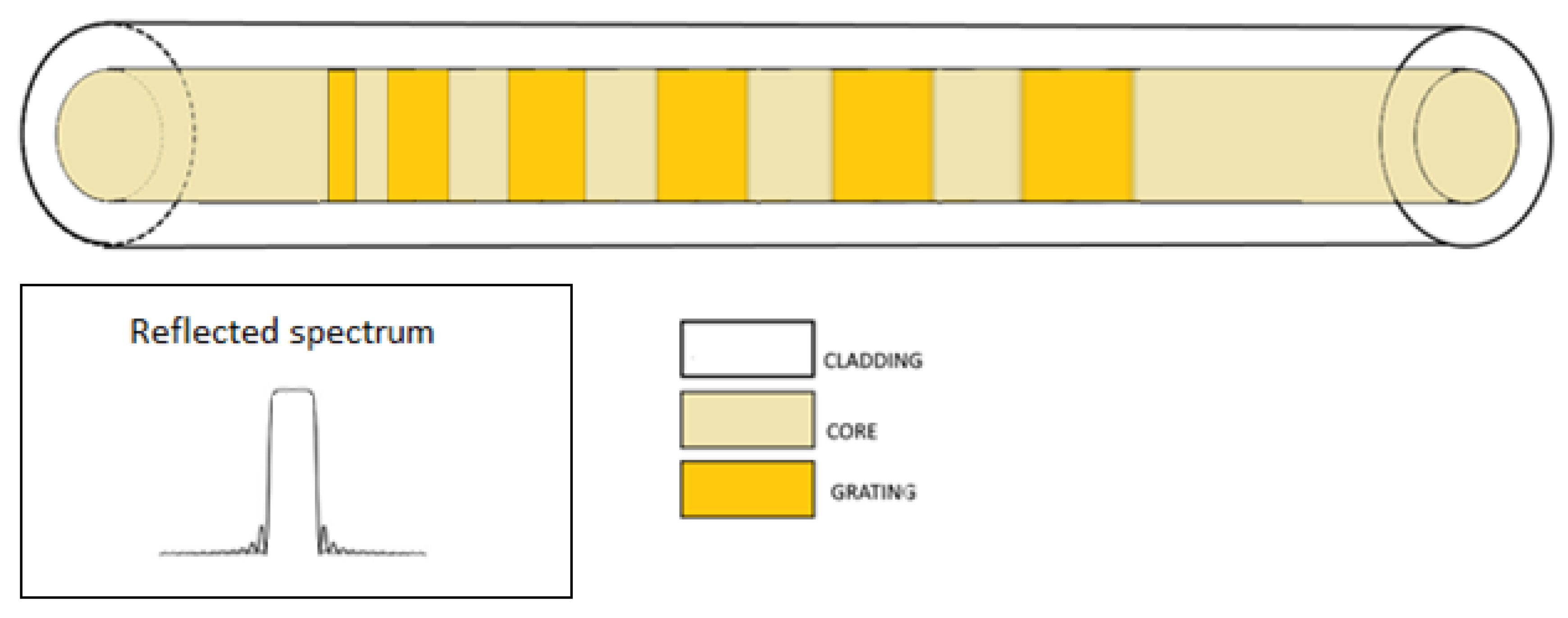
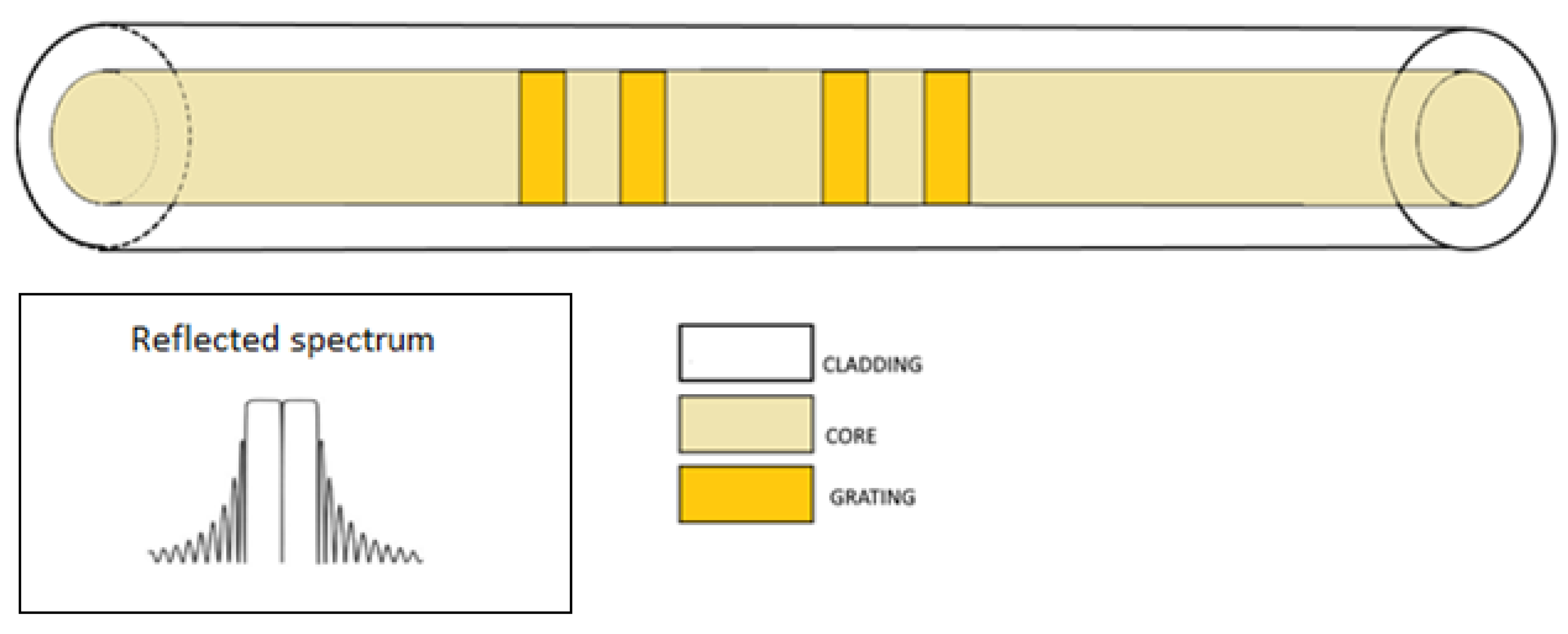


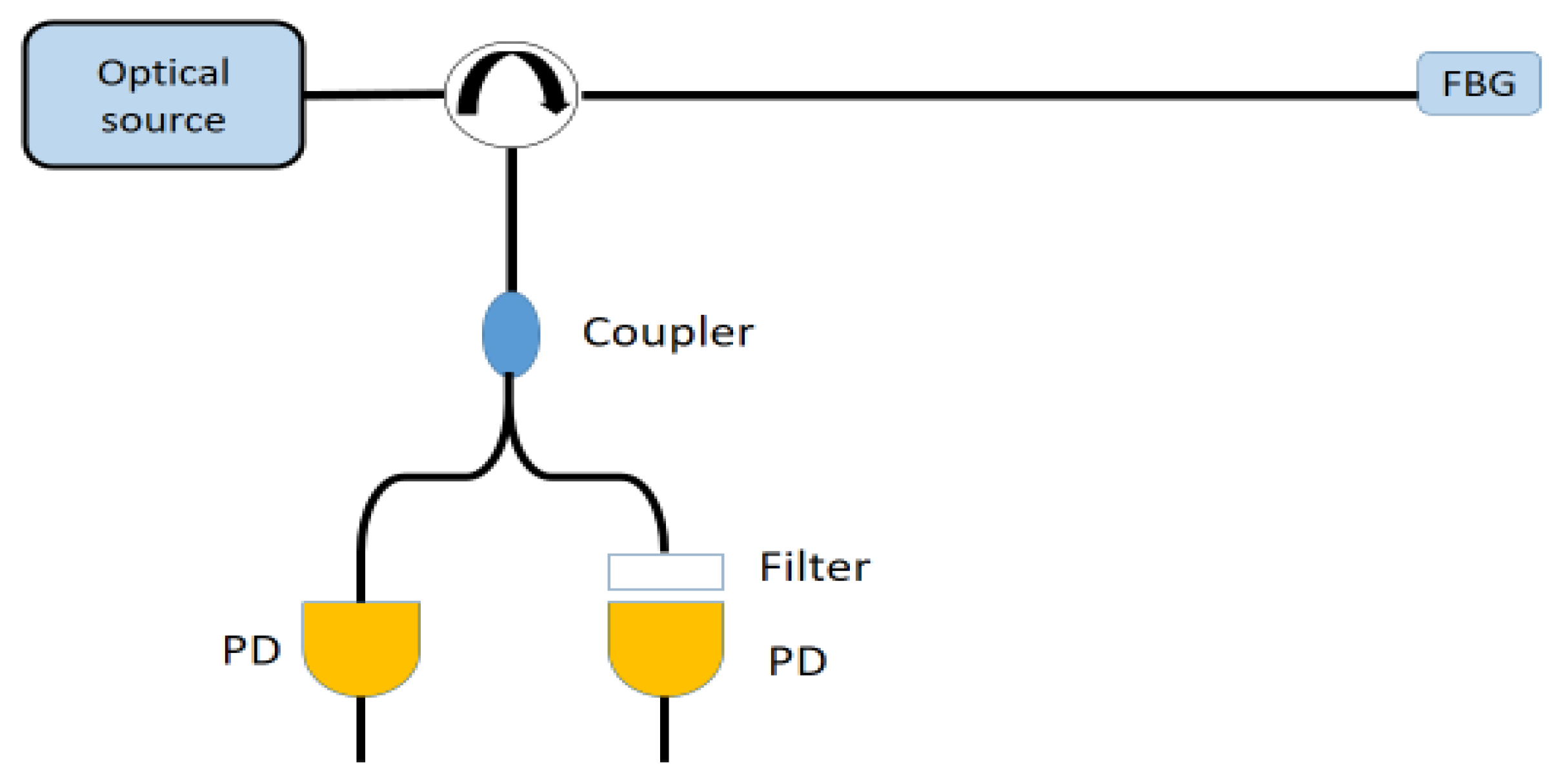
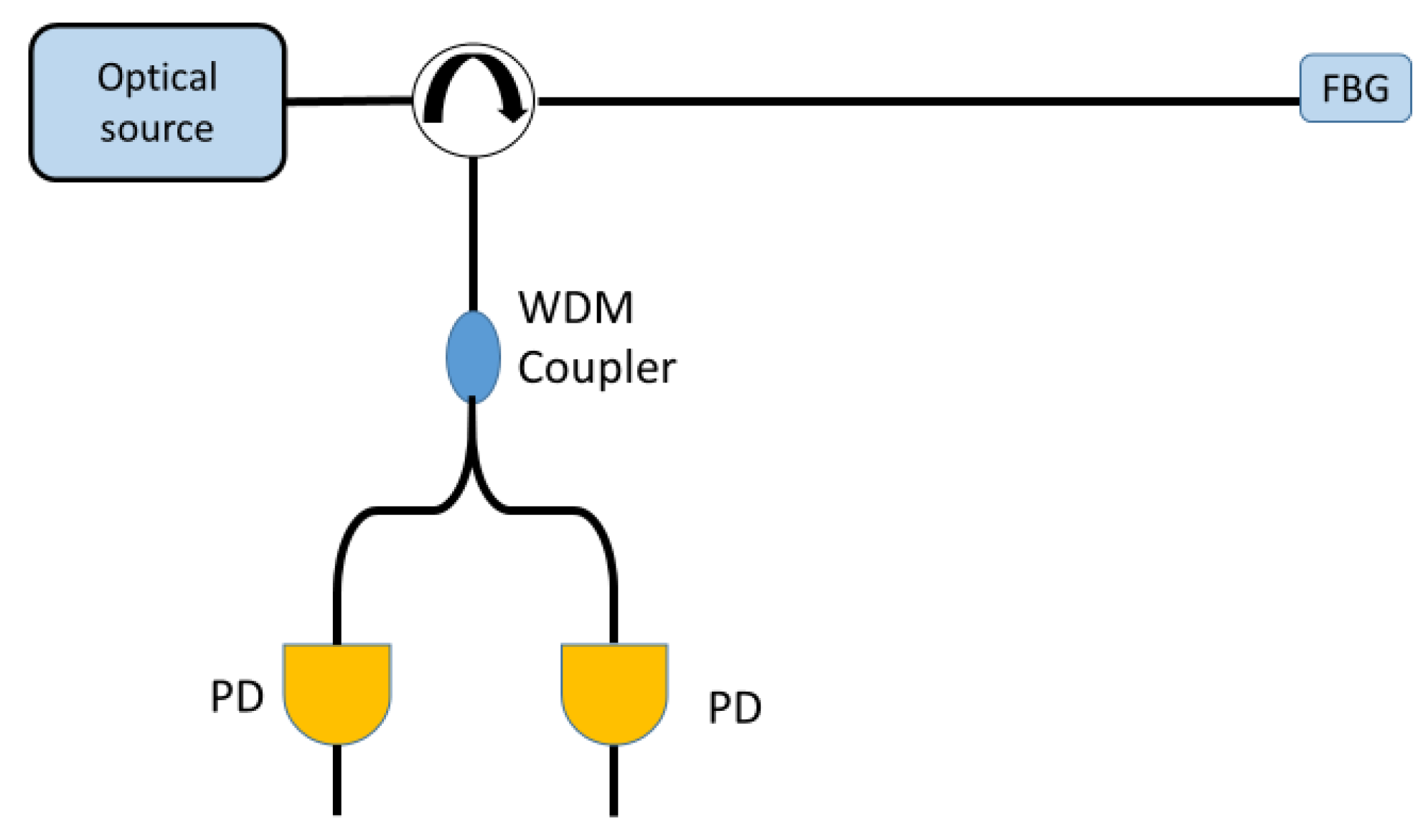
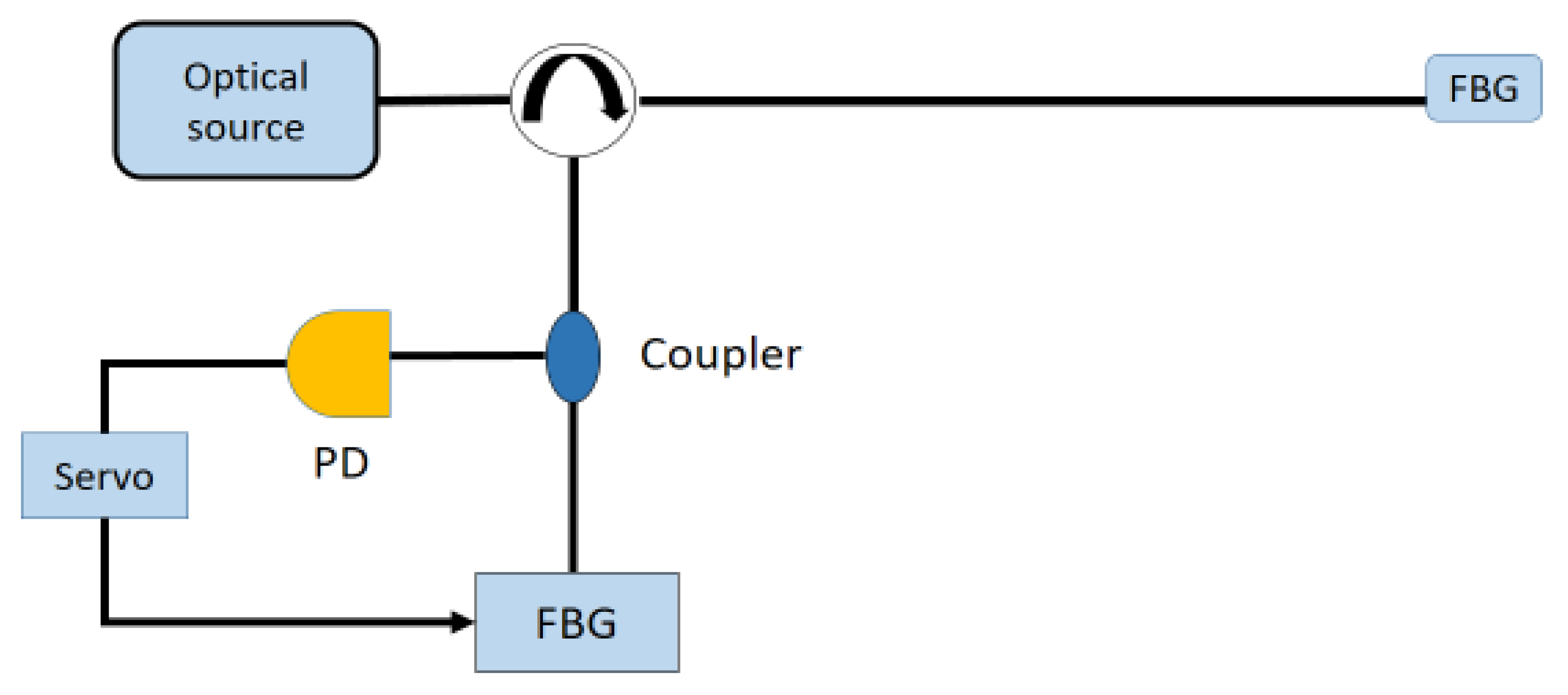
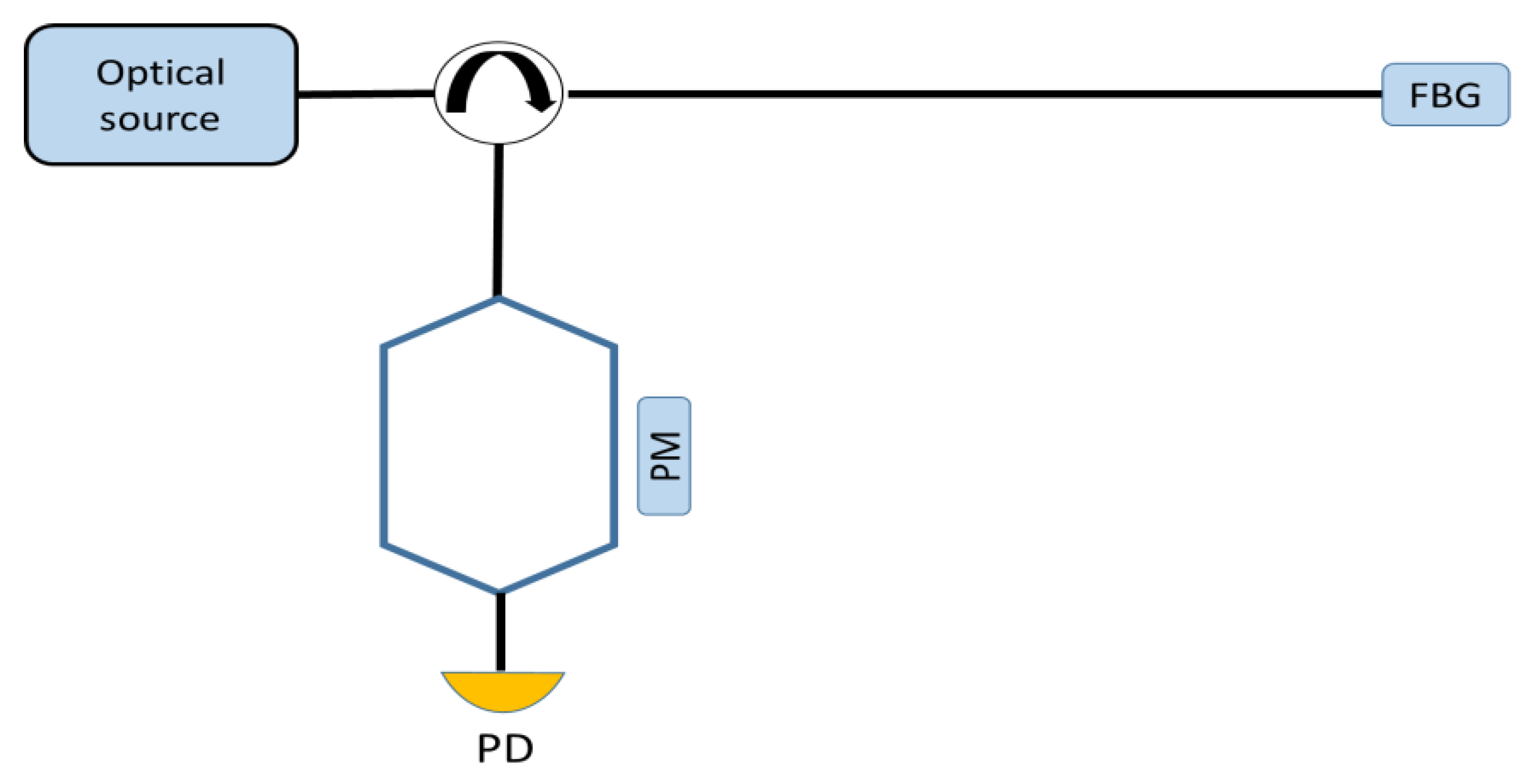
| Reference | Sensitivity | Detection Limit | Interrogation Technique | Punctual Optical Sensing Element | Perturbation |
|---|---|---|---|---|---|
| [50] | 1.10 pm/με | 26 µε | Laser, and mechanical stretching | All solid FBG | Static |
| [51] | 1.5 pm/με | Laser, optical analyser | FBG embedded with expansive material | Static | |
| [52] | 0.005 | Laser | Stretched polydimetilsiloxane (PDMS) micro-diffraction grating | Static | |
| [53] | Wavelength shift and FWHM of 104.1 pm/με and 61.6 pm/με respectively | 700 nε (active) | A broadband optical source OSA to perform readings | 3 mm long FBG written in photosensitive SMF | |
| [54] | Un-etched fibre Bragg grating 1.24 pm/με, Etched FBG 1.65 pm/με | Spectroscopic techniques OSA | Bragg grating pair, with one grating in the etched and the other in un-etched region of polymer fibre strain applied using a translation stage setup | Static | |
| [55] | 4.5 pm/με | Wavelength shift Through OSA | etched and regenerated FBG onto stretcher | Static | |
| [56] | 0.73 pm/με | Laser, reflectivity spectrum shift | dual-FBG strain sensor in PMMA single-mode microstructured POF | Static |
| Reference | Interrogation/Read-Out Technique | Features |
|---|---|---|
| [26] | Detected by a photodiode and visualized on a digital oscilloscope to measure splitting | resolution improvement |
| [30] | PDH to lock the laser to the FBG to measure splitting | resolution improvement |
| [57] | Radio-frequency modulation spectroscopic techniques | |
| [58] | Laser with post-processing sensitivity enhancement using FWM | sensitivity enhancement |
| [59] | Dual-comb spectroscopy | resolution improvement large dynamic range |
| [60] | Sideband interrogation technique (~2 MHz rf signals) to measure the resonance difference between a pair of FFPI | resolution improvement |
| [23] | Triangle wave driver Laser voltage, demodulation algorithm based on Gauss curve fitting and peak detection | resolution improvement |
| [61] | PDH technique | resolution improvement large dynamic range |
| [62] | Wavelength-swept fibre laser into unidirectional ring | simultaneous interrogation of quasi distributed sensor |
| [63] | Laser encoding Strain Signals. Read out using a H13C14N absorption line | resolution improvement |
| [64] | Dual-frequency OEO, ESA | thermal-insensitivity |
| [65] | Weak value amplification based on optical attenuation | sensitivity improvement |
| [66] | Double-sideband interrogation scheme | simultaneous measurement of strain and temperature |
| [67] | Radio-frequency modulation spectroscopic techniques | simultaneous measurement of strain and temperature |
| [68] | Change in voltage measured by Photodiode1. | temperature compensation |
| [69] | Tunable laser source controlled by the FBG modulated transmitted power | resolution improvement |
| [70] | Tunable laser source controlled by the FBG modulated transmitted power | resolution improvement |
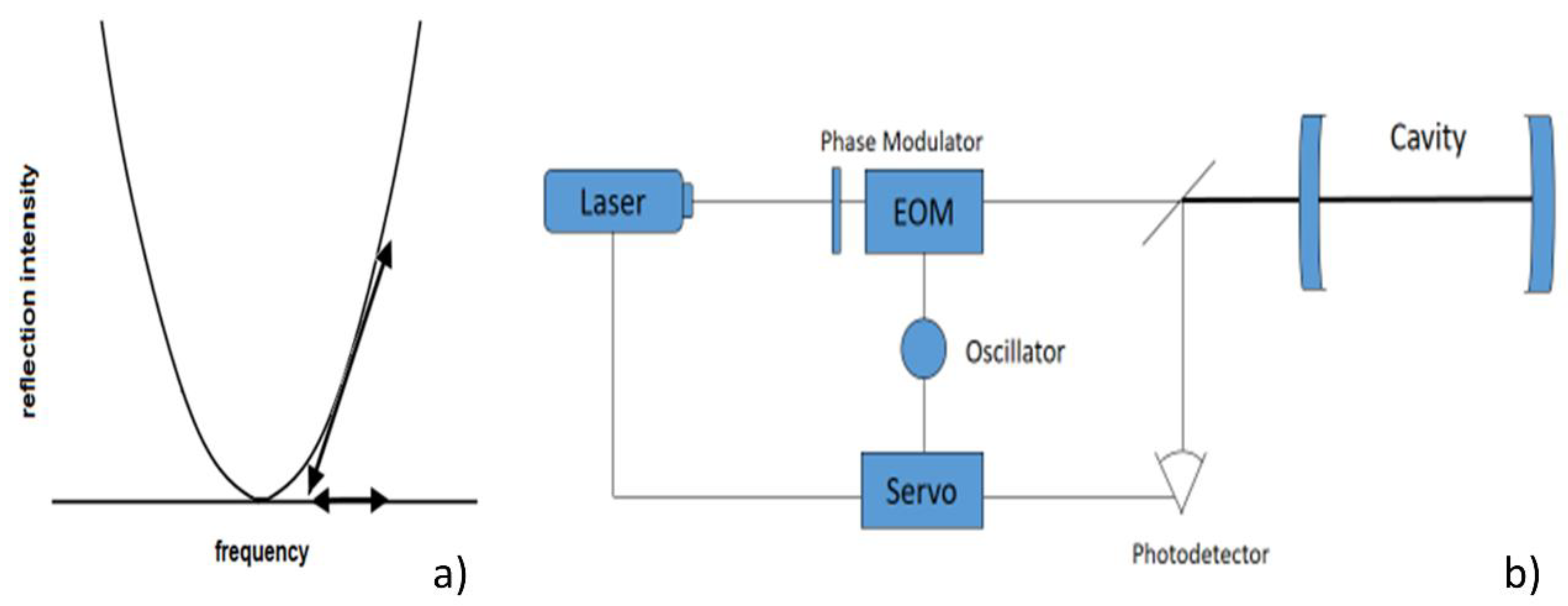
| [8] | PDH to lock the laser to the FBG | resolution improvement |
| [71] | PDH to lock the laser to the FBG | resolution improvement |
| Reference | Sensitivity | Detection Limit | Interrogation Technique | Punctual Optical Sensing Element | Perturbation |
|---|---|---|---|---|---|
| [72] | 1.1 pm/με | RMS error 9.5 pm | Spectrum ASE generated by EDF and passed through the FBG | FBG onto tensile stage system | static |
| [73] | 10 nε | Narrow line-width tuneable laser line-width 100 kHz | FBG onto two piers anchored to the rock and free FBG as reference | static | |
| [48] | 0.44 μϵ/√Hz | Resonant wavelength of the back-reflected spectrum from the grating | FBG strain gauge | quasi-static | |
| [74] | 2.6 nε | Tuneable laser | Pairs of equal FBG into two branches, one used as reference | static | |
| [75] | 1.4 pm/με | Laser | FBG onto cantilever | static |
| Oil & Gas | Energy | Military |
| Pipelines [76,77,78] Seismic [79,80] In-well [81] | Wind turbines [82] Geothermal [83] Smart Grids [84] | Hydrophones [85,86] Shipboard [87] |
| Industrial | Civil | Homeland Security |
| Process control [88] Machine tools [89] | Landslides [90] | Intrusion detection [91,92] Chemical detection [93] |
| Biomedical | Aerospace | Transportation |
| Heart rate Respiratory rate [94] Respiratory movement [95] MRI [94,95] | Fuselages [96,97] | Rail monitoring [98,99] |
| 3M Optical OEM Systems | [100] |
| Advanced Optical Solutions GmbH | [101] |
| AFW Technologies Pty Ltd. | [102] |
| Alcatel Optronics | [103] |
| Alxenses Company Ltd. | [104] |
| Ascentta Inc. | [105] |
| AtGrating (China) | [106] |
| Broptics Technology Inc. | [107] |
| DK Photonics Technology Co., Ltd. | [108] |
| FBG TECH | [109] |
| FBGS International NV | [110] |
| Fibreguide Industries | [111] |
| Gould Fibre Optic | [112] |
| HBM FibreSensing, S.A. | [113] |
| InPhoTech | [114] |
| ITF Technologies Inc. | [115] |
| iXBlue | [116] |
| Keysight | [117] |
| MPB Communications | [118] |
| Optoadvance S.r.l. | [119] |
| Optromix Co. | [120] |
| Oxford Lasers Inc | [121] |
| OZ Optics Limited | [122] |
| Proximion AB | [123] |
| Technica Optical Components, LLC | [124] |
| TeraXion | [125] |
| Thorlabs Inc. | [126] |
| VFIBRE Ltd. | [127] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campanella, C.E.; Cuccovillo, A.; Campanella, C.; Yurt, A.; Passaro, V.M.N. Fibre Bragg Grating Based Strain Sensors: Review of Technology and Applications. Sensors 2018, 18, 3115. https://doi.org/10.3390/s18093115
Campanella CE, Cuccovillo A, Campanella C, Yurt A, Passaro VMN. Fibre Bragg Grating Based Strain Sensors: Review of Technology and Applications. Sensors. 2018; 18(9):3115. https://doi.org/10.3390/s18093115
Chicago/Turabian StyleCampanella, Carlo Edoardo, Antonello Cuccovillo, Clarissa Campanella, Abdulkadir Yurt, and Vittorio M. N. Passaro. 2018. "Fibre Bragg Grating Based Strain Sensors: Review of Technology and Applications" Sensors 18, no. 9: 3115. https://doi.org/10.3390/s18093115
APA StyleCampanella, C. E., Cuccovillo, A., Campanella, C., Yurt, A., & Passaro, V. M. N. (2018). Fibre Bragg Grating Based Strain Sensors: Review of Technology and Applications. Sensors, 18(9), 3115. https://doi.org/10.3390/s18093115







