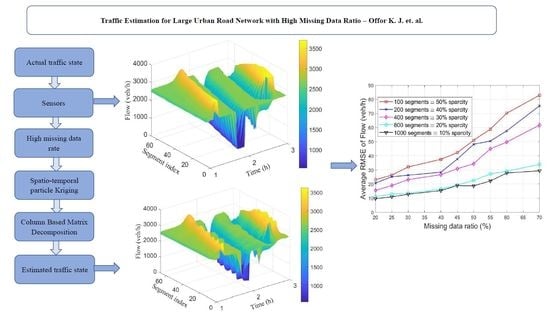
Traffic Estimation for Large Urban Road Network with High Missing Data Ratio
Abstract
:1. Introduction
2. Related Work
3. Model Formulation
3.1. Stochastic Compositional Traffic Flow Model
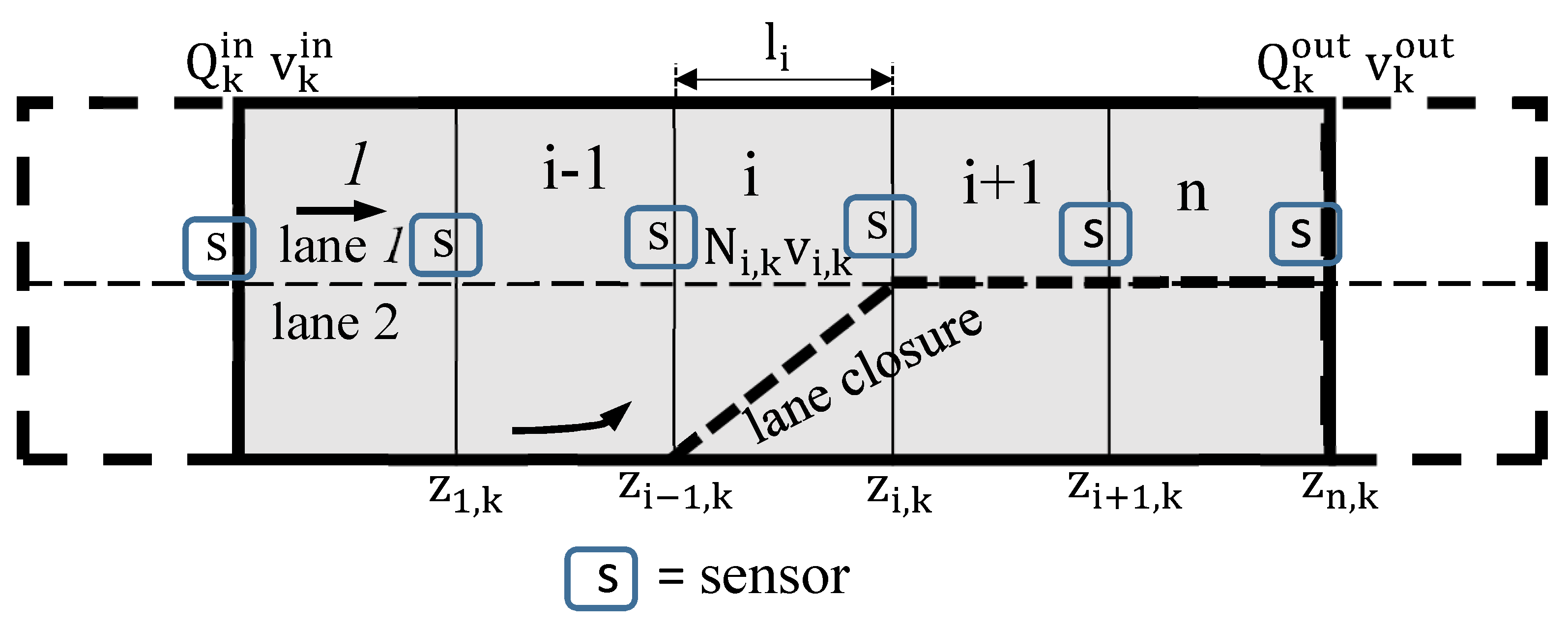
3.2. Measurement Model
4. Random Sets, Covariances and Variograms
4.1. Random Set
4.2. Covariance
5. Recursive Bayesian Estimation
5.1. Bayesian Estimation
5.2. Particle Filter
5.3. Missing Measurement Interpolation and Improved Likelihood Computation
| Algorithm 1 Particle Filter for Traffic State Estimation with Kriging Estimated Measurements [24] |
|
5.4. Missing Data Estimation via Kriging Models
6. Performance Evaluation
6.1. Simulation Design
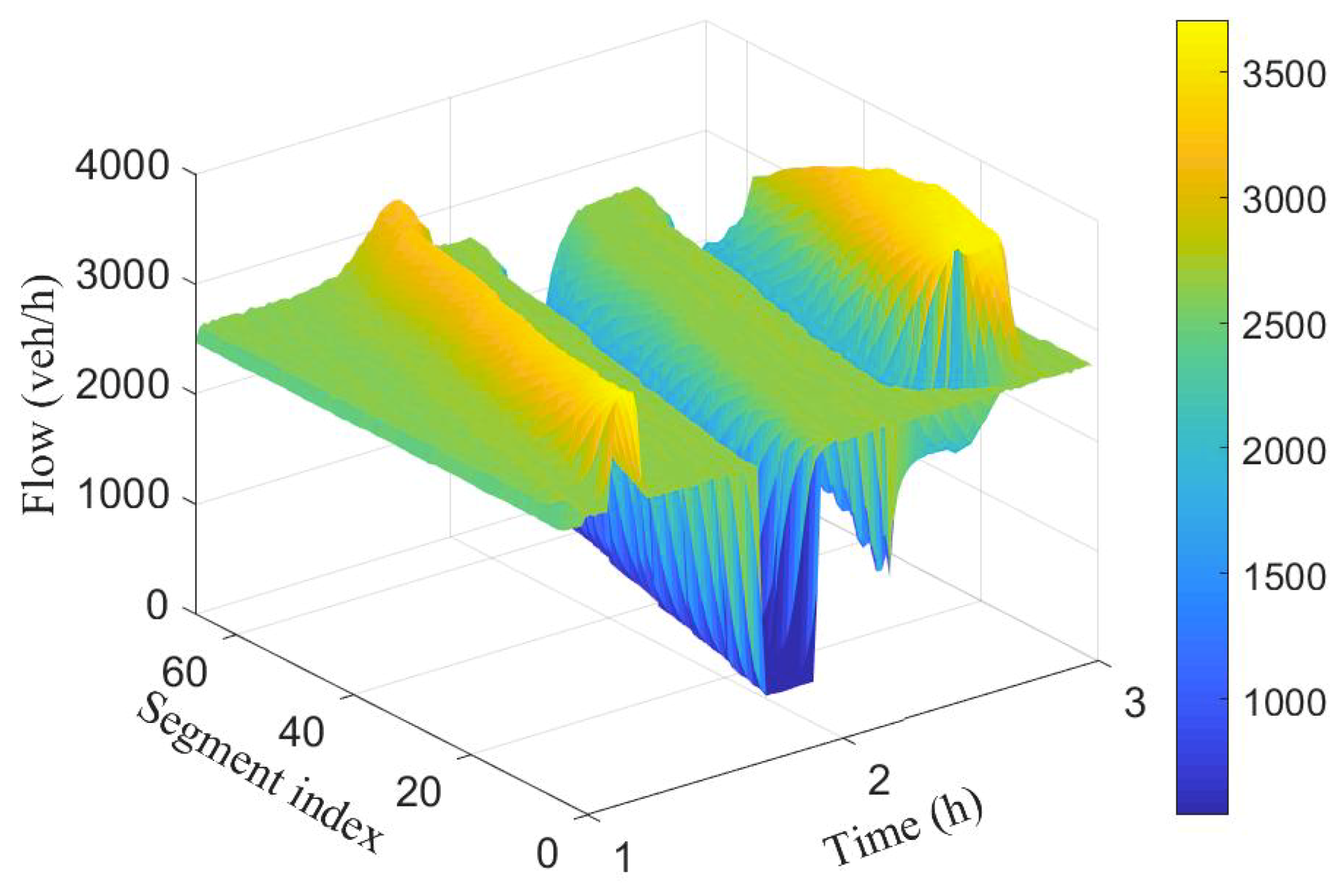
6.2. Results and Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ferrara, A.; Sacone, S.; Siri, S. State estimation in freeway traffic systems. In Freeway Traffic Modelling and Control. Advances in Industrial Control; Springer International Publishing: Cham, Switzerland, 2018; pp. 169–190. [Google Scholar]
- Seo, T.; Bayen, A.M.; Kusakabe, T.; Asakura, Y. Traffic state estimation on highway: A comprehensive survey. Annu. Rev. Control 2017, 43, 128–151. [Google Scholar] [CrossRef] [Green Version]
- Hoogendoorn, S.P.; Bovy, P.H.L. Generic gas-kinetic traffic systems modeling with applications to vehicular traffic flow. Transp. Res. Part B 2001, 35, 317–336. [Google Scholar] [CrossRef]
- Papageorgiou, M.; Ben-Akiva, M.; Bottom, J.; Bovy, P.H.L.; Hoogendoorn, S.P.; Hounsell, N.B.; Kotsialos, A.; Mcdonald, M. ITS and traffic management. In Handbooks in Operations Research and Management Science; Elsevier: Amsterdam, The Netrerlands, 2007; Chapter 11; Volume 14. [Google Scholar]
- Pipes, L.A. An operational analysis of traffic dynamics. J. Appl. Phys. 1953, 24, 274–281. [Google Scholar] [CrossRef]
- Gipps, P.G. A behavioural car-following model for computer simulation. Transp. Res. Part B Methodol. 1981, 15, 105–111. [Google Scholar] [CrossRef]
- Hao, Z.; Boel, R.; Li, Z. Model based urban traffic control, part I: Local model and local model predictive controllers. Transp. Res. Part C Emerg. Technol. 2018, 97, 61–81. [Google Scholar] [CrossRef]
- Hao, Z.; Boel, R.; Li, Z. Model based urban traffic control, part II: Local model and local model predictive controllers. Transp. Res. Part C Emerg. Technol. 2018, 97, 23–44. [Google Scholar] [CrossRef]
- Messmer, A.; Papageorgiou, M. METANET: A macroscopic simulation program for motorway networks. Traffic Eng. Control 1990, 31, 466–470. [Google Scholar]
- Daganzo, C.F. The cell transmission model: A dynamic representation of highway traffic consistent with the hydrodynamic theory. Transp. Res. Part B 1994, 28, 269–287. [Google Scholar] [CrossRef]
- Lu, H.-P.; Sun, Z.-Y.; Qu, W.-C. Big data-driven based real-time traffic flow state identification and prediction. Discret. Dyn. Nat. Soc. 2015, 2015, 1–11. [Google Scholar] [CrossRef]
- Braxmeier, H.; Schmidt, V.; Spodarev, E. Kriged road-traffic maps. In Interfacing Geostatistics and GIS; Pilz, J., Ed.; Springer: Heidelberg, Germany, 2009; Chapter 9; pp. 105–119. [Google Scholar]
- Lowry, M. Spatial interpolation of traffic counts based on origin-destination centrality. J. Transp. Geogr. 2014, 36, 98–105. [Google Scholar] [CrossRef]
- Wang, X.; Kockelman, K.M.; Murray, W.J. Forecasting network data: Spatial interpolation of traffic counts from Texas data. Transp. Res. Rec. 2009, 2105, 100–108. [Google Scholar] [CrossRef]
- Gastaldi, M.; Gecchele, G.; Rossi, R. Estimation of annual average daily traffic from one-week traffic counts. A combined ANN-Fuzzy approach. Transp. Res. Part C Emerg. Technol. 2014, 47, 86–99. [Google Scholar] [CrossRef]
- Zou, H.; Yue, Y.; Li, Q.; Yeh, O.G.A. An improved distance metric for the interpolation of link-based traffic data using kriging: A case study of a large-scale urban road network. Int. J. Geogr. Inf. Sci. 2012, 26, 667–689. [Google Scholar] [CrossRef]
- Song, Y.; Wang, X.; Wright, G.; Thatcher, D.; Wu, P.; Felix, P. Traffic volume prediction with segment-based regression Kriging and its implementation in assessing the impact of heavy vehicles. IEEE Trans. Intell. Transp. Syst. 2019, 20, 234–243. [Google Scholar] [CrossRef]
- Yang, H.; Yang, J.; Han, L.D.; Liu, X.; Pu, L.; Chin, S.-M.; Hwang, H.-L. A Kriging based spatiotemporal approach for traffic volume data imputation. PLoS ONE 2018, 13, 1–11. [Google Scholar] [CrossRef]
- Krige, D.G. A statistical approach to some basic mine problems on the Witwatersrand. J. Chem. Metall. Soc. S. Min. Afr. 1951, 52, 119–139. [Google Scholar]
- Matheron, G. Principles of geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Zhang, Y. A comparative study of three multivariate short-term freeway traffic flow forecasting methods with missing data. J. Intell. Transp. Syst. 2016, 20, 205–218. [Google Scholar] [CrossRef]
- Ladino, A.; Kibangou, Y.; Fourati, H.; Canudas de Wit, C. Travel time forecasting from clustered time series via optimal fusion strategy. In Proceedings of the 2016 European Control Conference (ECC), Aalborg, Denmark, 29 June–1 July 2016. [Google Scholar]
- Hawes, M.; Amer, H.M.; Mihaylova, L. Traffic state estimation via a particle filter with compressive sensing and historical traffic data. In Proceedings of the 2016 19th International Conference on Information Fusion (FUSION), Heidelberg, Germany, 5–8 July 2016; pp. 735–742. [Google Scholar]
- Mihaylova, L.; Boel, R.; Hegyi, A. Freeway traffic estimation within particle filtering framework. Automatica 2007, 43, 290–300. [Google Scholar] [CrossRef] [Green Version]
- Offor, K.J.; Hawes, M.; Mihaylova, L.S. Short term traffic flow prediction with particle methods in the presence of sparse data. In Proceedings of the 2018 21st International Conference on Information Fusion (FUSION), Cambridge, UK, 10–13 July 2018; pp. 1205–1212. [Google Scholar]
- Hawes, M.; Amer, H.M.; Mihaylova, L. Traffic state estimation via a particle filter over a reduced measurement space. In Proceedings of the 2017 20th International Conference on Information Fusion (Fusion), Xi’an, China, 10–13 July 2017. [Google Scholar]
- Li, Y.; Li, Z.; Li, L. Missing traffic data: Comparison of imputation methods. IET Intell. Transp. Syst. 2014, 8, 51–57. [Google Scholar] [CrossRef]
- Nychka, D.; Bandyopadhyay, S.; Hammerling, D.; Lindgren, F. A multiresolution Gaussian process model for the analysis of large spatial datasets. J. Comput. Graph. Stat. 2015, 24, 579–599. [Google Scholar] [CrossRef]
- Katzfuss, M.; Hammerling, D. Parallel inference for massive distributed spatial data using low-rank models. Stat. Comput. 2017, 27, 363–375. [Google Scholar] [CrossRef]
- Katzfuss, M. A multi-resolution approximation for massive spatial datasets. J. Am. Stat. Assoc. 2017, 112, 201–214. [Google Scholar] [CrossRef]
- Boel, R.; Mihaylova, L. A compositional stochastic model for real-time freeway traffic simulation. Transp. Res. Part B Methodol. 2006, 40, 319–334. [Google Scholar] [CrossRef]
- Gustafsson, F. Particle filter theory and practice with positioning applications. IEEE Aerosp. Electron. Syst. Mag. 2010, 25, 53–82. [Google Scholar] [CrossRef]
- Mitrovic, N.; Asif, M.T.; Dauwels, J.; Jaillet, P. Low-dimensional models for compressed sensing and prediction of large-scale traffic data. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2949–2954. [Google Scholar] [CrossRef]
- Behrisch, M.; Bieker, L.; Erdmann, J.; Krajzewicz, D. SUMO—Simulation of urban mobility—An overview. In Proceedings of the SIMUL 2011, The Third International Conference on Advances in System Simulation, Barcelona, Spain, 23–28 Oktober 2011; pp. 63–68. [Google Scholar]
- Mihaylova, L.; Hegyi, A.; Gning, A.; Boel, R.K. Parallelized particle and Gaussian sum particle filters for large-scale freeway traffic systems. IEEE Trans. Intell. Transp. Syst. 2012, 13, 36–48. [Google Scholar] [CrossRef]






| Car | Bus | |
|---|---|---|
| Max speed | 25 m/s | 20 m/s |
| Acceleration | 1.0 m/s | 0.8 m/s |
| Deceleration | 4.5 m/s | 4.5 m/s |
| Sigma (driver perfection) | 0.5 | 0.5 |
| Length | 5 m | 10 m |
| Minimum Separation | 2.5 m | 3 m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Offor, K.J.; Vaci, L.; Mihaylova, L.S. Traffic Estimation for Large Urban Road Network with High Missing Data Ratio. Sensors 2019, 19, 2813. https://doi.org/10.3390/s19122813
Offor KJ, Vaci L, Mihaylova LS. Traffic Estimation for Large Urban Road Network with High Missing Data Ratio. Sensors. 2019; 19(12):2813. https://doi.org/10.3390/s19122813
Chicago/Turabian StyleOffor, Kennedy John, Lubos Vaci, and Lyudmila S. Mihaylova. 2019. "Traffic Estimation for Large Urban Road Network with High Missing Data Ratio" Sensors 19, no. 12: 2813. https://doi.org/10.3390/s19122813