Dynamic Load Balancing of Software-Defined Networking Based on Genetic-Ant Colony Optimization
Abstract
1. Introduction
2. Related Work
2.1. SDN
2.2. ACO
2.3. GA
2.4. LB of SDN
3. The Proposed Scheme
3.1. LB with ACO
- If α is small, it depends mainly on the value of dij.
- If β is small, it is selected randomly.
3.2. The Proposed G-ACO Scheme
| Procedure 1. Crossover operation of G-ACO |
| 1: Assume that the path of P1 is (x1, y1, z1) and that of P2 is (x2, y2, z2). The crossover operation occurs with y1 and y2, and one of the new paths obtained is P3: (x1, y2, y1, z1). |
| 2: Deleting the duplicated switch, the new path P3 is determined. 3: By the same way, another new path P4 is obtained. 4: Applying the fitness function to P1, P2, P3, P4, an optimal path is selected |
| Procedure 2. Mutation operation of G-ACO |
| 1: The mutation occurrence is based on the frequency which is defined in the simulation part, and the number of switches in the optimal path is m. |
| 2: Randomly generate two natural numbers, n1 and n2 (n2 < n1 < m). 3: By exchanging the switch at the location of n1 and n2 of the optimal path, P0, a new path, Pn is obtained. 4: Obtain the fitness of P0 and Pn, and the one of the smaller value is selected as the optimal path |
| Procedure 3. LB with G-ACO |
| 1: Nc + = 1; (Iteration times) |
| 2: Ak = 1; 3: Ak selects the next switch based on the calculated probability of Equation (2); meanwhile, update the taboo table and path pheromone. 4: k + = 1; 5: If k ≤ m (the total number of ants), go to Step 3, otherwise execute the GA; 6: Obtain the fitness value, and if the value satisfies the constraint, exits the loop. Otherwise, jump back to Step 1 |
4. Performance Evaluation
4.1. Environment of Experiment
- Supports relevant protocols of SDN such as OpenFlow
- Supports open Python API for developers
- Supports relevant modules of SDN such as Open vSwitch
- Highly scalable
- Developers can customize the topologies as needed
- Supports co-development among several engineers
- Topology Manager: Responsible for the entire network topology
- Forwarding Rule Manager: Manages the actions of entire network by adding, searching, deleting, and updating the flow rules
- Service Abstract Layer: Core module of OpenDayLight, abstracting some parts of the network by southbound interface and supporting application layer
- Host Tracker: Manages the information of the hosts by keeping the IP and MAC address, and establishes and deletes the connections to northbound interface
- Stats Manager: Manages the whole information of the network
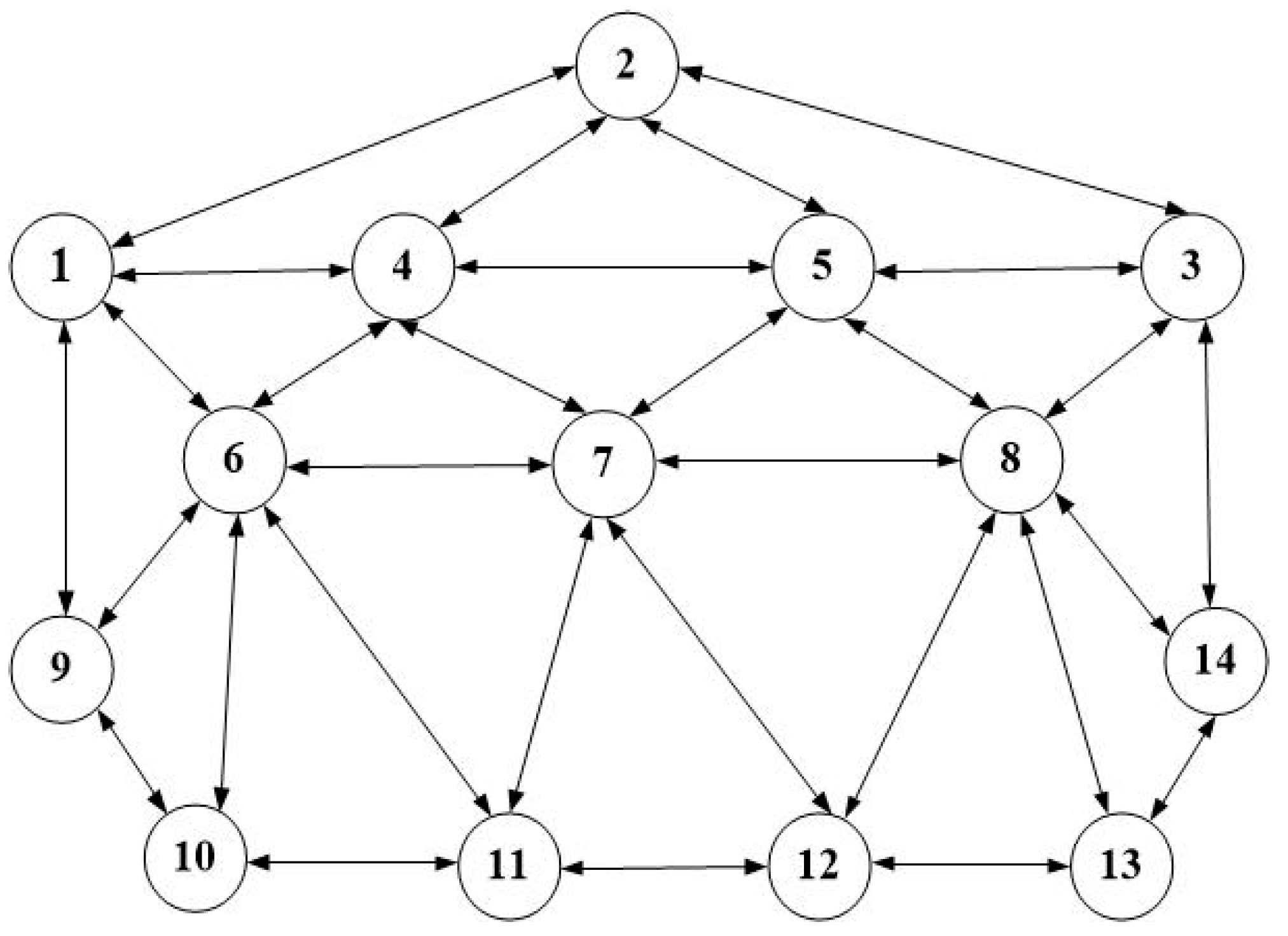
4.2. Test Topology
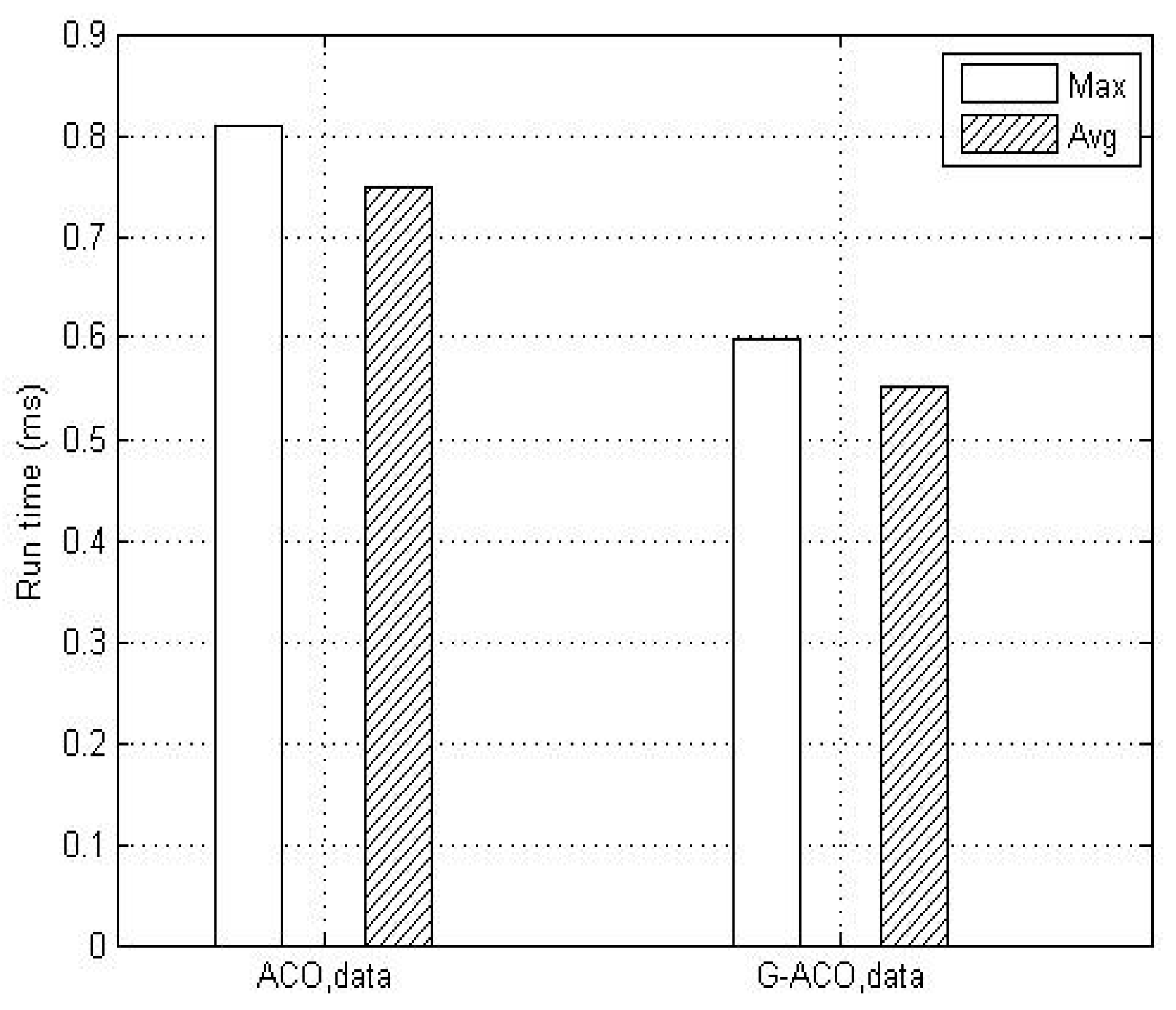
4.3. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kreutz, D.; Ramos, F.M.V.; Verissimo, P.E.; Rothenberg, C.E.; Azodolmolky, S.; Uhlig, S. Software-Defined Networking: A Comprehensive Survey. Proc. IEEE 2015, 103, 14–76. [Google Scholar] [CrossRef]
- Kang, S.B.; Kwon, G.I. Load Balancing Strategy of SDN Controller Based on Genetic Algorithm. Adv. Sci. Technol. Lett. 2016, 129, 219–222. [Google Scholar]
- Li, Y.J.; Li, X.B.; Osamu, Y. Traffic Engineering Framework with Machine Learning based Meta-Layer in Software-Defined Networks. In Proceedings of the 4th IEEE International Conference on Network Infrastructure and Digital Content (IC-NIDC), Beijing, China, 19–21 September 2014. [Google Scholar]
- Dobrijevic, O.; Santl, M.; Matijasevic, M. Ant Colony Optimization for QoE-Centric Flow Routing in Software-Defined Networks. In Proceedings of the 11th International Conference on Network and Service Management (CNSM), Barcelona, Spain, 9–13 November 2015. [Google Scholar]
- Lin, W.C.; Zhang, L.C. The Load Balancing Research of SDN based on Ant Colony Algorithm with Job Classification. In Proceedings of the 2nd Workshop on Advanced Research and Technology in Industry Applications, Dalian, China, 14–15 May 2016. [Google Scholar]
- Kim, H.J.; Feamster, N. Improving network management with software defined networking. IEEE Commun. Mag. 2013, 51, 114–119. [Google Scholar] [CrossRef]
- Shin, M.K.; Nam, K.H.; Kim, H.J. Software-defined networking (SDN): A reference architecture and open APIs. In Proceedings of the 2012 International Conference on ICT Convergence (ICTC’12), Jeju Island, South Korea, 15–17 October 2012. [Google Scholar]
- OpenFlowv1.3.0. Available online: http://www.brocade.com/content/html/en/configuration-guide/netiron-05900-sdnguide/GUID-B26EC8DB-D5A7-422E-94A0-94CC981595B3.html (accessed on 12 July 2017).
- Zhang, H.L.; Guo, X. SDN-Based Load Balancing Strategy for Server Cluster. In Proceedings of the IEEE 3rd International Conference on Cloud Computing and Intelligence Systems (CCIS), Shenzhen, China, 27–29 November 2014. [Google Scholar]
- Hsiao, Y.T.; Chuang, C.L.; Chien, C.C. Computer network load-balancing and routing by ant colony optimization. In Proceedings of the 12th IEEE International Conference on Networks (ICON 2004), Singapore, Singapore, 16–19 November 2004. [Google Scholar]
- Janacik, P.; Orfanus, D.; Wilke, A. A survey of ant colony optimization-based approaches to routing in computer networks. In Proceedings of the 4th International Conference on Intelligent Systems Modeling & Simulation (ISMS), Bangkok, Thailand, 29–31 January 2013. [Google Scholar]
- Wikipedia, Genetic Algorithm. Available online: https://en.wikipedia.org/wiki/Genetic_algorithm (accessed on 13 July 2017).
- Sathyanarayana, S.; Moh, M. Joint Rout-Server Load Balancing in Software Defined Networks using Ant Colony Optimization. In Proceedings of the 2016 International Conference on High Performance Computing & Simulation (HPCS), Innsbruck, Austria, 18–22 July 2016. [Google Scholar]
- Wang, Y.L.; Yuan, K.J.; Fang, W.; Liu, Y.H.; Jun, M. Research of a SDN Traffic Scheduling Technology Based on Ant Colony Algorithm. In Proceedings of the International Conference on Information Engineering and Communications Technology (IECT 2016), Shanghai, China, 21–22 May 2016. [Google Scholar]
- Gomes, B.T.P.; Muniz, L.C.M.; Silva, F.J.S.; Santos, D.V.; Lopes, R.F.; Coutinho, L.R.; Carvalho, F.O.; Endler, M. A Middleware with Comprehensive Quality of Context Support for the Internet of Things Applications. Sensors 2017, 17, 2853. [Google Scholar] [CrossRef] [PubMed]
- Davis, L. Applying adaptive algorithm to Epistatic Domains. In Proceedings of the International Joint Conference on Artificial Intelligence, Los Angeles, California, 18–23 August 1985. [Google Scholar]
- Mininet. Available online: http://mininet.org/overview/ (accessed on 15 July 2017).
- OpenDayLight Project. Available online: https://en.wikipedia.org/wiki/OpenDaylight_Project (accessed on 15 July 2017).
- Jo, E.; Pan, D.; Liu, J.; Butler, L. A simulation and emulation study of SDN-based multipath routing for fat-tree data center networks. In Proceedings of the Simulation Conference (WSC), Savanah, GA, USA, 11–14 December 2014. [Google Scholar]
- Charles, E. LEISERSON. Fat-Trees: Universal Networks for Hardware-Efficient Supercomputing. IEEE Trans. Comput. 1985, 34, 892–901. [Google Scholar]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- iPerf—The TCP, UDP and SCTP Network Bandwidth Measurement Tool. Available online: https://iperf.fr (accessed on 18 July 2017).










| Field | Description |
|---|---|
| Match | Port, packet header, and metadata forwarded from the previous flow table |
| Priority | Matching precedence of the entry |
| Counter | Statistics for matching the packets |
| Instruction | Action or pipeline processing |
| Timeout | Maximum effective time or free time before the entry is overdue |
| Cookie | Opaque data sent by the OpenFlow controller |
| PC1 | PC2 | |
|---|---|---|
| OS | Windows 10 | Ubuntu 16.04 |
| Virtual Machine | VMware Workstation 12 (OS: Ubuntu 16.04) | None |
| CPU | i3-4150 | i3-4350 |
| RAM | 8G | 8G |
| Hard Disk | 500G | 500G |
| Pheromone Volatilization Factor (ρ) | Iterations |
|---|---|
| 0.1 | 3 |
| 0.3 | 7 |
| 0.5 | 8 |
| 0.7 | 13 |
| 0.9 | 28 |
| α | B | Iterations |
|---|---|---|
| 0.1 | 0.1 | 33 |
| 0.1 | 0.5 | 17 |
| 0.5 | 0.5 | 8 |
| 1 | 2 | 7 |
| 3 | 7 | 3 |
| 5 | 9 | 2 |
| M | Iterations |
|---|---|
| 2 | 20 |
| 4 | 12 |
| 6 | 10 |
| 8 | 9 |
| 10 | 2 |
| Destination | RR & ACO | G-ACO |
|---|---|---|
| h2 | h1-e7-h2 | h1-e7-h2 |
| h3 | h1-e7-a3-e8-h3 | h1-e7-a4-e8-h3 |
| h4 | h1-e7-a3-e8-h4 | h1-e7-a4-e8-h4 |
| h5 | h1-e7-a3-c2-a6-e9-h5 | h1-e7-a4-c1-a6-e9-h5 |
| h6 | h1-e7-a3-c2-a6-e9-h6 | h1-e7-a4-c1-a6-e9-h6 |
| h7 | h1-e7-a3-c2-a6-e10-h7 | h1-e7-a3-c1-a6-e10-h7 |
| h8 | h1-e7-a3-c2-a6-e10-h8 | h1-e7-a3-c1-a6-e10-h8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, H.; Kim, K.T.; Youn, H.Y. Dynamic Load Balancing of Software-Defined Networking Based on Genetic-Ant Colony Optimization. Sensors 2019, 19, 311. https://doi.org/10.3390/s19020311
Xue H, Kim KT, Youn HY. Dynamic Load Balancing of Software-Defined Networking Based on Genetic-Ant Colony Optimization. Sensors. 2019; 19(2):311. https://doi.org/10.3390/s19020311
Chicago/Turabian StyleXue, Hai, Kyung Tae Kim, and Hee Yong Youn. 2019. "Dynamic Load Balancing of Software-Defined Networking Based on Genetic-Ant Colony Optimization" Sensors 19, no. 2: 311. https://doi.org/10.3390/s19020311
APA StyleXue, H., Kim, K. T., & Youn, H. Y. (2019). Dynamic Load Balancing of Software-Defined Networking Based on Genetic-Ant Colony Optimization. Sensors, 19(2), 311. https://doi.org/10.3390/s19020311




