Frequency Dependency of the Delta-E Effect and the Sensitivity of Delta-E Effect Magnetic Field Sensors
Abstract
:1. Introduction
2. The Delta-E Effect
2.1. The ΔE-Effect
2.2. Frequency Dependency of the Young’s Modulus
2.3. Dynamic Differential Susceptibility
3. Results and Discussion
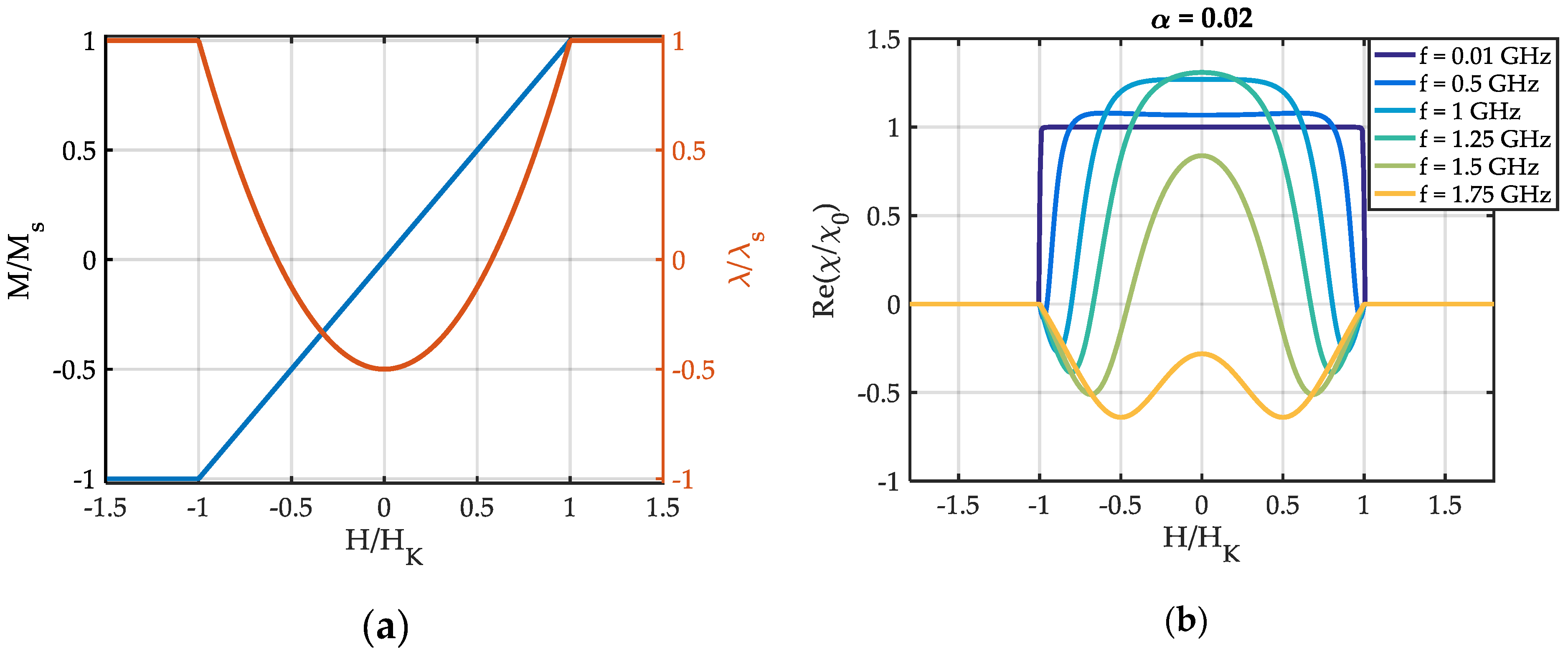
3.1. Frequency Dependency of the Young’s Modulus and Dynamic Susceptibility
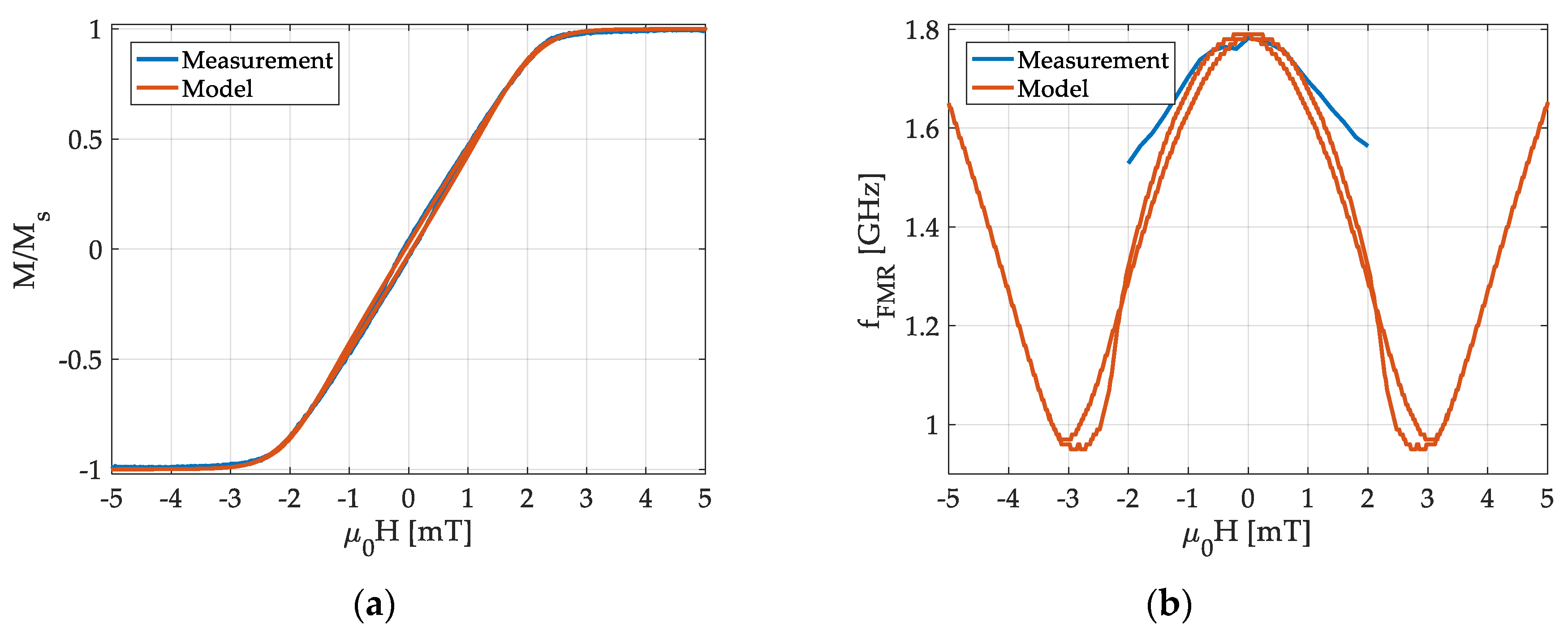
3.2. Mean-Field Calculations and Measurements
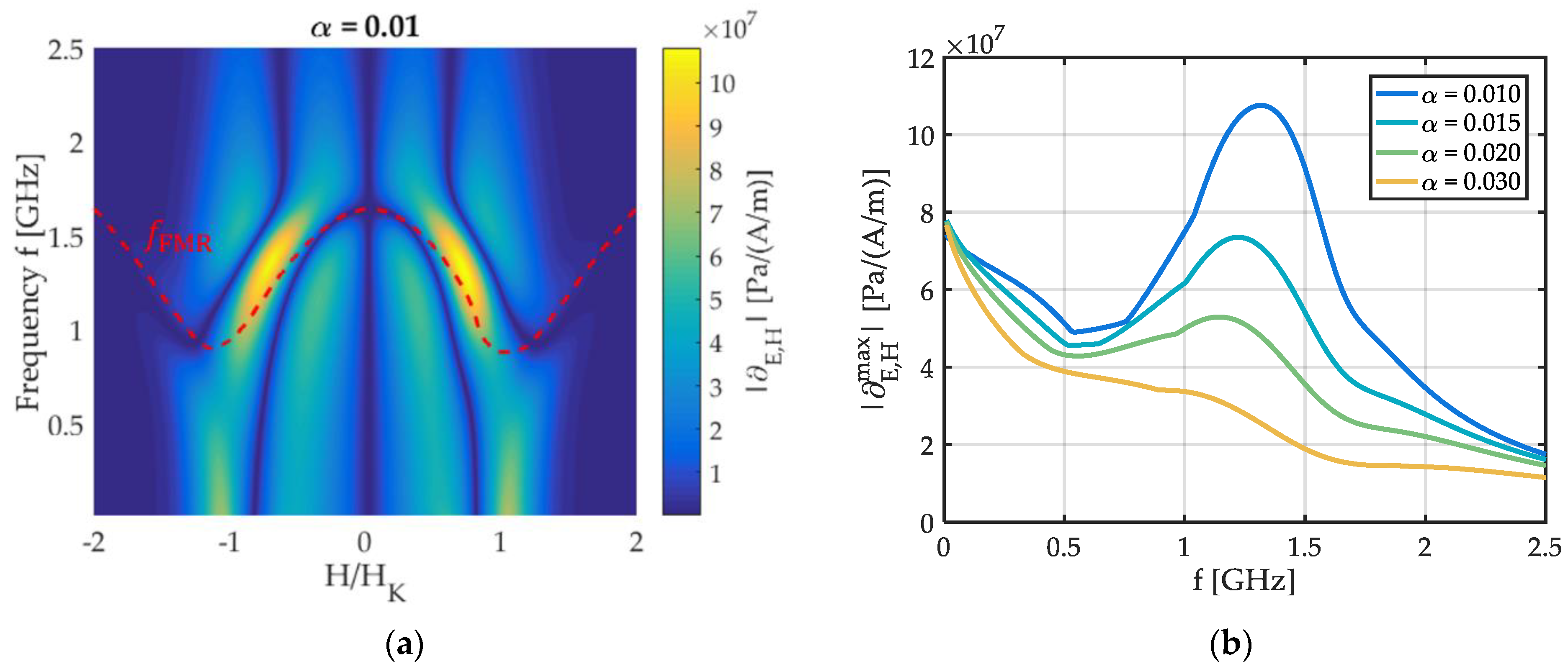
3.3. The Magnetic Sensitivity of Delta-E Effect Sensors
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Calculation of the Dynamic Suceptibility
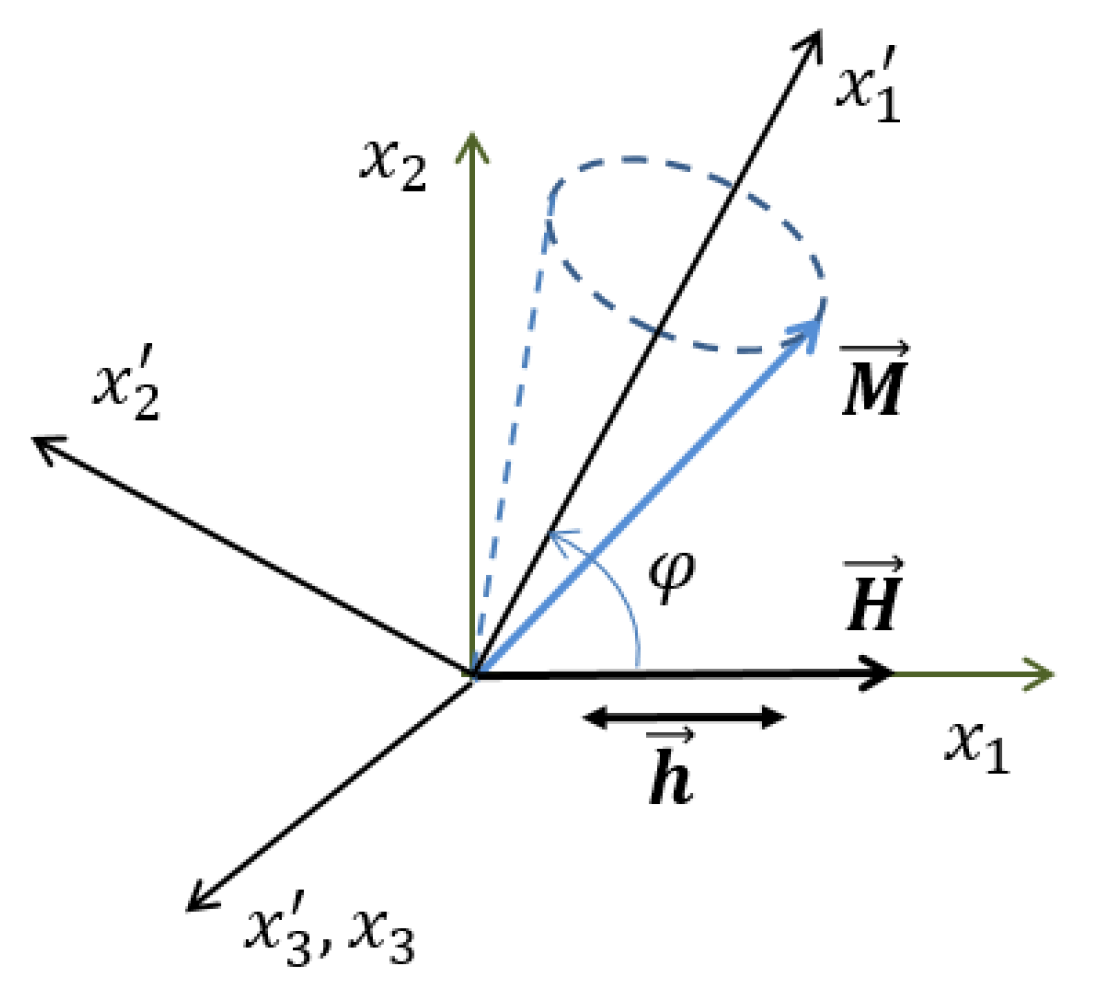
Appendix A.2. Magnetic Mean-Field Model
Appendix A.3. Model Parameters for Figure 1
Appendix A.4. Measurements
References
- Kneller, E. Ferromagnetismus; Springer-Verlag OHG: Berlin/Göttingen/Heidelberg, 1962; ISBN 978-3-642-86695-1. [Google Scholar]
- Livingston, J.D. Magnetomechanical properties of amorphous metals. Phys. Status Solidi A 1982, 70, 591–596. [Google Scholar] [CrossRef]
- Lee, E.W. Magnetostriction and Magnetomechanical Effects. Reports Prog. Phys. 1955, 18, 184–229. [Google Scholar] [CrossRef]
- Gojdka, B.; Jahns, R.; Meurisch, K.; Greve, H.; Adelung, R.; Quandt, E.; Knöchel, R.; Faupel, F. Fully integrable magnetic field sensor based on delta-E effect. Appl. Phys. Lett. 2011, 99, 1–4. [Google Scholar] [CrossRef]
- Jahns, R.; Zabel, S.; Marauska, S.; Gojdka, B.; Wagner, B.; Knöchel, R.; Adelung, R.; Faupel, F. Microelectromechanical magnetic field sensor based on the delta-E effect. Appl. Phys. Lett. 2014, 105, 2012–2015. [Google Scholar] [CrossRef]
- Zabel, S.; Kirchhof, C.; Yarar, E.; Meyners, D.; Quandt, E.; Faupel, F. Phase modulated magnetoelectric delta-E effect sensor for sub-nano tesla magnetic fields. Appl. Phys. Lett. 2015, 107. [Google Scholar] [CrossRef]
- Zabel, S.; Reermann, J.; Fichtner, S.; Kirchhof, C.; Quandt, E.; Wagner, B.; Schmidt, G.; Faupel, F. Multimode delta-E effect magnetic field sensors with adapted electrodes. Appl. Phys. Lett. 2016, 108, 222401. [Google Scholar] [CrossRef]
- Nan, T.; Hui, Y.; Rinaldi, M.; Sun, N.X. Self-biased 215 MHz magnetoelectric NEMS resonator for ultra-sensitive DC magnetic field detection. Sci Rep 2013, 3, 1985. [Google Scholar] [CrossRef]
- Hui, Y.; Nan, T.; Sun, N.X.; Rinaldi, M. High resolution magnetometer based on a high frequency magnetoelectric MEMS-CMOS oscillator. J. Microelectromechanical Syst. 2015, 24, 134–143. [Google Scholar] [CrossRef]
- Li, M.; Matyushov, A.; Dong, C.; Chen, H.; Lin, H.; Nan, T.; Qian, Z.; Rinaldi, M.; Lin, Y.; Sun, N.X. Ultra-sensitive NEMS magnetoelectric sensor for picotesla DC magnetic field detection. Appl. Phys. Lett. 2017, 110, 143510. [Google Scholar] [CrossRef]
- Tu, C.; Chu, Z.-Q.; Spetzler, B.; Hayes, P.; Dong, C.-Z.; Liang, X.-F.; Chen, H.-H.; He, Y.-F.; Wei, Y.-Y.; Lisenkov, I.; et al. Mechanical-Resonance-Enhanced Thin-Film Magnetoelectric Heterostructures for Magnetometers, Mechanical Antennas, Tunable RF Inductors, and Filters. Materials 2019, 12, 2259. [Google Scholar] [CrossRef] [PubMed]
- Hanna, S.M. Magnetic Field Sensors Based on SAW Propagation in Magnetic Films. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1987, 34, 191–194. [Google Scholar] [CrossRef] [PubMed]
- Liur, X. Enhanced sensitivity of temperature- compensated SAW-based current sensor using the magnetostrictive effect. Smart Mater. Struct. 2016, 26, 025008. [Google Scholar]
- Polewczyk, V.; Dumesnil, K.; Lacour, D.; Moutaouekkil, M.; Mjahed, H.; Tiercelin, N.; Petit Watelot, S.; Mishra, H.; Dusch, Y.; Hage-Ali, S.; et al. Unipolar and bipolar high-magnetic-field sensors based on surface acoustic wave resonators. Phys. Rev. Appl. 2017, 8, 1–11. [Google Scholar] [CrossRef]
- Kittmann, A.; Durdaut, P.; Zabel, S.; Reermann, J.; Schmalz, J.; Spetzler, B.; Meyners, D.; Sun, N.X.; McCord, J.; Gerken, M.; et al. Wide Band Low Noise Love Wave Magnetic Field Sensor System. Sci. Rep. 2018, 8, 1–10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, X.; Tong, B.; Ou-Yang, J.; Yang, X.; Chen, S.; Zhang, Y.; Zhu, B. Self-biased vector magnetic sensor based on a Love-type surface acoustic wave resonator. Appl. Phys. Lett. 2018, 113. [Google Scholar] [CrossRef]
- Mazzamurro, A.; Talbi, A.; Dusch, Y.; Elmazria, O.; Pernod, P.; Matar, O.B.; Tiercelin, N. Highly Sensitive Surface Acoustic Wave Magnetic Field Sensor Using Multilayered TbCo2/FeCo Thin Film. Proceedings 2018, 2, 902. [Google Scholar] [CrossRef]
- Webb, D.C.; Forester, D.W.; Ganguly, A.K.; Vittoria, C. Applications of amorphous magnetic-layers in surface-acoustic-wave devices. IEEE Trans. Magn. 1979, 15, 1410–1415. [Google Scholar] [CrossRef]
- Robbins, W.P.; Hietala, A. A Simple Phenomenological Model of Tunable SAW Devices Using Magnetostrictive Thin Films. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1988, 35, 718–722. [Google Scholar] [CrossRef]
- Wiegert, R.F.; Levy, M. Enhanced magnetically tunable attenuation and relative velocity of 0.6 GHz Rayleigh waves in nickel thin films. Appl. Phys. Lett. 1989, 54, 995–997. [Google Scholar] [CrossRef]
- Wiegert, R.F. Magnetoelastic surface acoustic wave attenuation and anisotropic magnetoresistance in Ni[sub 3]Fe thin films. J. Appl. Phys. 2002, 91, 8231. [Google Scholar] [CrossRef]
- Smole, P.; Ruile, W.; Korden, C.; Ludwig, A.; Quandt, E.; Krassnitzer, S.; Pongratz, P. Magnetically tunable SAW-resonator. In Proceedings of the IEEE International Frequency Control Symposium and PDA Exhibition Jointly with the 17th European Frequency and Time Forum, Tampa, FL, USA, 4–8 May 2003; pp. 4–7. [Google Scholar]
- Sun, N.X.; Srinivasan, G. Voltage Control of Magnetism in Multiferroic Heterostructures and Devices. Spin 2012, 2, 1240004. [Google Scholar] [CrossRef]
- Liu, X.; Ou-Yang, J.; Tong, B.; Chen, S.; Zhang, Y.; Zhu, B.; Yang, X. Influence of the delta-E effect on a surface acoustic wave resonator. Appl. Phys. Lett. 2019, 114, 062903. [Google Scholar] [CrossRef]
- Mason, W.P. Domain Wall Relaxation in Nickel. Phys. Rev. 1949, 83, 683. [Google Scholar] [CrossRef]
- Johnson, S.J.; Rogers, T.F. Magnetically induced ultrasonic velocity changes in polycrystalline nickel. J. Appl. Phys. 1952, 23, 574–577. [Google Scholar] [CrossRef]
- Mason, W.P. Rotational Relaxation in Nickel at High Frequencies. Rev. Mod. Phys. 1953, 25. [Google Scholar] [CrossRef]
- Squire, P.T. Phenomenological model for magnetization, magnetostriction and delta-E effect in field-annealed amorphous ribbons. J. Magn. Magn. Mater. 1990, 87, 299–310. [Google Scholar] [CrossRef]
- Squire, P.T. Domain model for magnetoelastic behaviour of uniaxial ferromagnets. J. Magn. Magn. Mater. 1995, 140–144, 1829–1830. [Google Scholar] [CrossRef]
- Datta, S.; Atulasimha, J.; Mudivarthi, C.; Flatau, A.B. Stress and magnetic field-dependent Young’s modulus in single crystal iron-gallium alloys. J. Magn. Magn. Mater. 2010, 322, 2135–2144. [Google Scholar] [CrossRef]
- Bou Matar, O.; Robillard, J.F.; Vasseur, J.O.; Hladky-Hennion, A.C.; Deymier, P.A.; Pernod, P.; Preobrazhensky, V. Band gap tunability of magneto-elastic phononic crystal. J. Appl. Phys. 2012, 111. [Google Scholar] [CrossRef]
- Zhou, H.; Talbi, A.; Tiercelin, N.; Bou Matar, O. Multilayer magnetostrictive structure based surface acoustic wave devices. Appl. Phys. Lett. 2014, 104, 114101. [Google Scholar] [CrossRef]
- Daniel, L.; Hubert, O. An analytical model for the Δ E effect in magnetic materials. Eur. Phys. J. Appl. Phys. 2009, 45, 31101. [Google Scholar] [CrossRef]
- Hubert, O.; Daniel, L. Measurement and Analytical Modeling of the delta-E Effect in a Bulk Iron-Cobalt Alloy. IEEE Trans. Magn. 2010, 46, 401–404. [Google Scholar] [CrossRef]
- Zhang, D.G.; Li, M.H.; Zhou, H.M. A general one-dimension nonlinear magneto-elastic coupled constitutive model for magnetostrictive. AIP Adv. 2015, 5. [Google Scholar] [CrossRef]
- Ganguly, A.K.; Davis, K.L.; Webb, D.C.; Vittoria, C. Magnetoelastic surface waves in a magnetic film-piezoelectric substrate configuration. J. Appl. Phys. 1976, 47, 2696–2704. [Google Scholar] [CrossRef]
- Ganguly, A.K.; Davis, K.L.; Webb, D.C. Magnetoelastic surface waves on the (110) plane of highly magnetostrictive cubic crystals. J. Appl. Phys. 1978, 49, 759–767. [Google Scholar] [CrossRef]
- Walikainen, D.; Wiegert, R.F.; Levy, M. Magnetic Field Dependency of 600 MHz SAW Velocity Changes For Thin Ni Films. In Proceedings of the Ultrasonics Symposium, Chicago, IL, USA, 2–5 October 1988; Volume 192, pp. 173–180. [Google Scholar]
- Weiler, M.; Dreher, L.; Heeg, C.; Huebl, H.; Gross, R.; Brandt, M.S.; Goennenwein, S.T.B. Elastically driven ferromagnetic resonance in nickel thin films. Phys. Rev. Lett. 2011, 106, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Dreher, L.; Weiler, M.; Pernpeintner, M.; Huebl, H.; Gross, R.; Brandt, M.S.; Goennenwein, S.T.B. Surface Acoustic Wave-Driven Ferromagnetic Resonance in Nickel Thin Films: Theory and Experiment. Phys. Rev. B 2012, 134415, 1–13. [Google Scholar] [CrossRef]
- Becker, R.; Döring, W. Ferromagnetismus; Verlag von Julius Springer: Berlin, 1939; ISBN 9783642471124. [Google Scholar]
- Ludwig, A.; Quandt, E. Optimization of the delta E effect in thin films and multilayers by magnetic field annealing. IEEE Trans. Magn. 2002, 38, 2829–2831. [Google Scholar] [CrossRef]
- Sárközi, Z.; Mackay, K.; Peuzin, J.C. Elastic properties of magnetostrictive thin films using bending and torsion resonances of a bimorph. J. Appl. Phys. 2000, 88, 5827–5832. [Google Scholar] [CrossRef]
- O’handley, R.C. Modern Magnetic Materials Principles and Applications; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2000; ISBN 978-0-471-15566-9. [Google Scholar]
- Reid, A.H.; Shen, X.; Maldonado, P.; Chase, T.; Granitzka, P.W.; Carva, K.; Li, R.K.; Li, J.; Wu, L.; Vecchione, T.; et al. Beyond a phenomenological description of magnetostriction. Nat. Commun. 2018, 9. [Google Scholar] [CrossRef]
- Stoner, E.C.; Wohlfarth, E.P. A Mechanism of Magnetic Hysteresis in Heterogeneous Alloys. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 240, 599–642. [Google Scholar] [CrossRef]
- Gilbert, T.L. A phenomenological theory of damping in ferromagnetic materials. IEEE Trans. Magn. 2004, 40, 3443–3449. [Google Scholar] [CrossRef]
- Gurevich, A.G.; Melkov, G.A. Magnetizaton Oscillation and Waves; CRC Press: Boca Raton, FL, USA, 1996; ISBN 978-0849394607. [Google Scholar]
- Panina, L.V.; Mohri, K.; Uchiyama, T.; Noda, M. Giant Magneto-Impedance in Co-Rich Amorphous Wires and Films. IEEE Trans. Magn. 1995, 31, 1249–1260. [Google Scholar] [CrossRef]
- Kraus, L. GMI modeling and material optimization. Sens. Actuators A Phys. 2003, 106, 187–194. [Google Scholar] [CrossRef]
- Kittel, C. On the theory of ferromagnetic resonance absorption. Phys. Rev. 1948, 73, 155–161. [Google Scholar] [CrossRef]
- Gebert, A.; McCord, J.; Schmutz, C.; Quandt, E. Permeability and Magnetic Properties of Ferromagnetic NiFe/FeCoBSi Bilayers for High-Frequency Applications. IEEE Trans. Magn. 2007, 43, 2624–2626. [Google Scholar]
- Neudert, A.; McCord, J.; Schäfer, R.; Schultz, L. Dynamic anisotropy in amorphous CoZrTa films. J. Appl. Phys. 2004, 95, 6595–6597. [Google Scholar] [CrossRef]
- Hoffmann, H. Theory of magnetization ripple. IEEE Trans. Magn. 1968, 4, 32–38. [Google Scholar] [CrossRef]
- Rantschler, J.O.; Alexander, C. Ripple field effect on high-frequency measurements of FeTiN films. J. Appl. Phys. 2003, 93, 6665–6667. [Google Scholar] [CrossRef]
- Aharoni, A. Demagnetizing factors for rectangular ferromagnetic prisms. J. Appl. Phys. 1998, 83, 3432–3434. [Google Scholar] [CrossRef]
- Silva, T.J.; Lee, C.S.; Crawford, T.M.; Rogers, C.T. Inductive measurement of ultrafast magnetization dynamics in thin-film Permalloy. J. Appl. Phys. 1999, 85, 7849–7862. [Google Scholar] [CrossRef] [Green Version]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spetzler, B.; Golubeva, E.V.; Müller, C.; McCord, J.; Faupel, F. Frequency Dependency of the Delta-E Effect and the Sensitivity of Delta-E Effect Magnetic Field Sensors. Sensors 2019, 19, 4769. https://doi.org/10.3390/s19214769
Spetzler B, Golubeva EV, Müller C, McCord J, Faupel F. Frequency Dependency of the Delta-E Effect and the Sensitivity of Delta-E Effect Magnetic Field Sensors. Sensors. 2019; 19(21):4769. https://doi.org/10.3390/s19214769
Chicago/Turabian StyleSpetzler, Benjamin, Elizaveta V. Golubeva, Cai Müller, Jeffrey McCord, and Franz Faupel. 2019. "Frequency Dependency of the Delta-E Effect and the Sensitivity of Delta-E Effect Magnetic Field Sensors" Sensors 19, no. 21: 4769. https://doi.org/10.3390/s19214769




