Spatiotemporal Rule of Heat Transfer on a Soil/Finned Tube Interface
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
- The soil surrounding the gravity-assisted heat pipe is isotropous, and the temperature distribution is homogeneous at a given depth;
- The thermal contact resistance at the interface is not considered;
- No internal heat is generated.
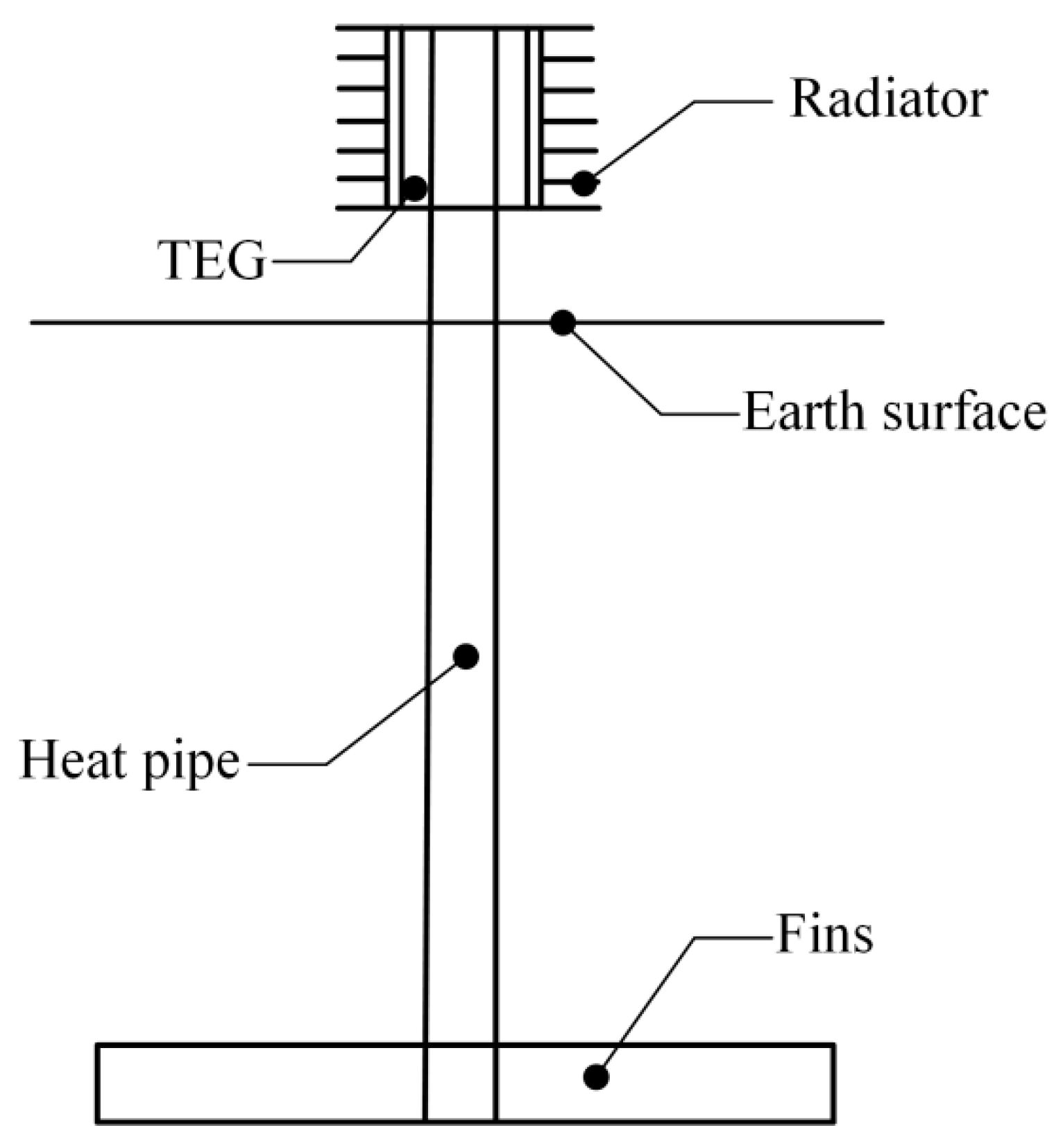
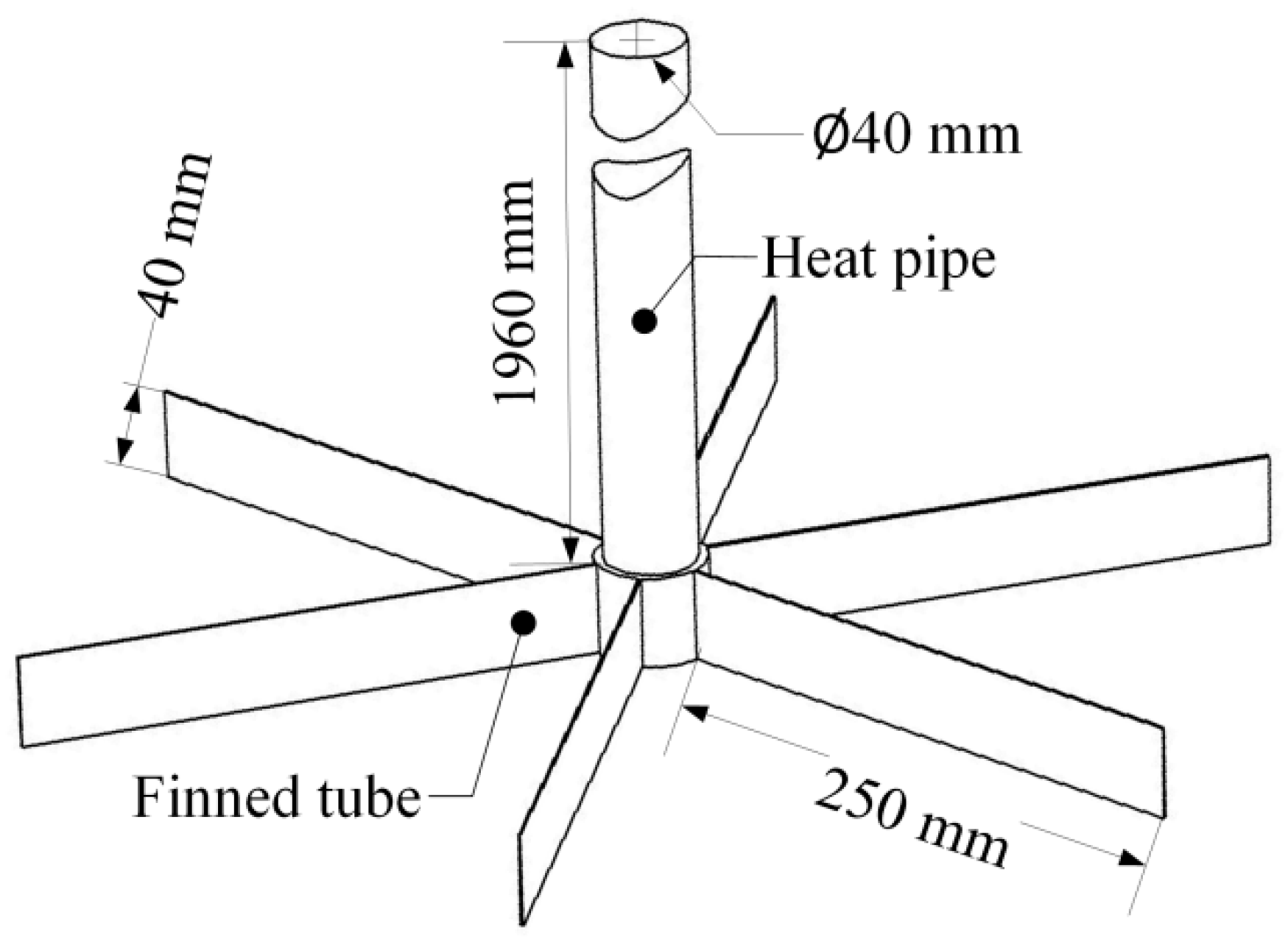
2.2. Set-up of the Model
2.3. Mathematics Model
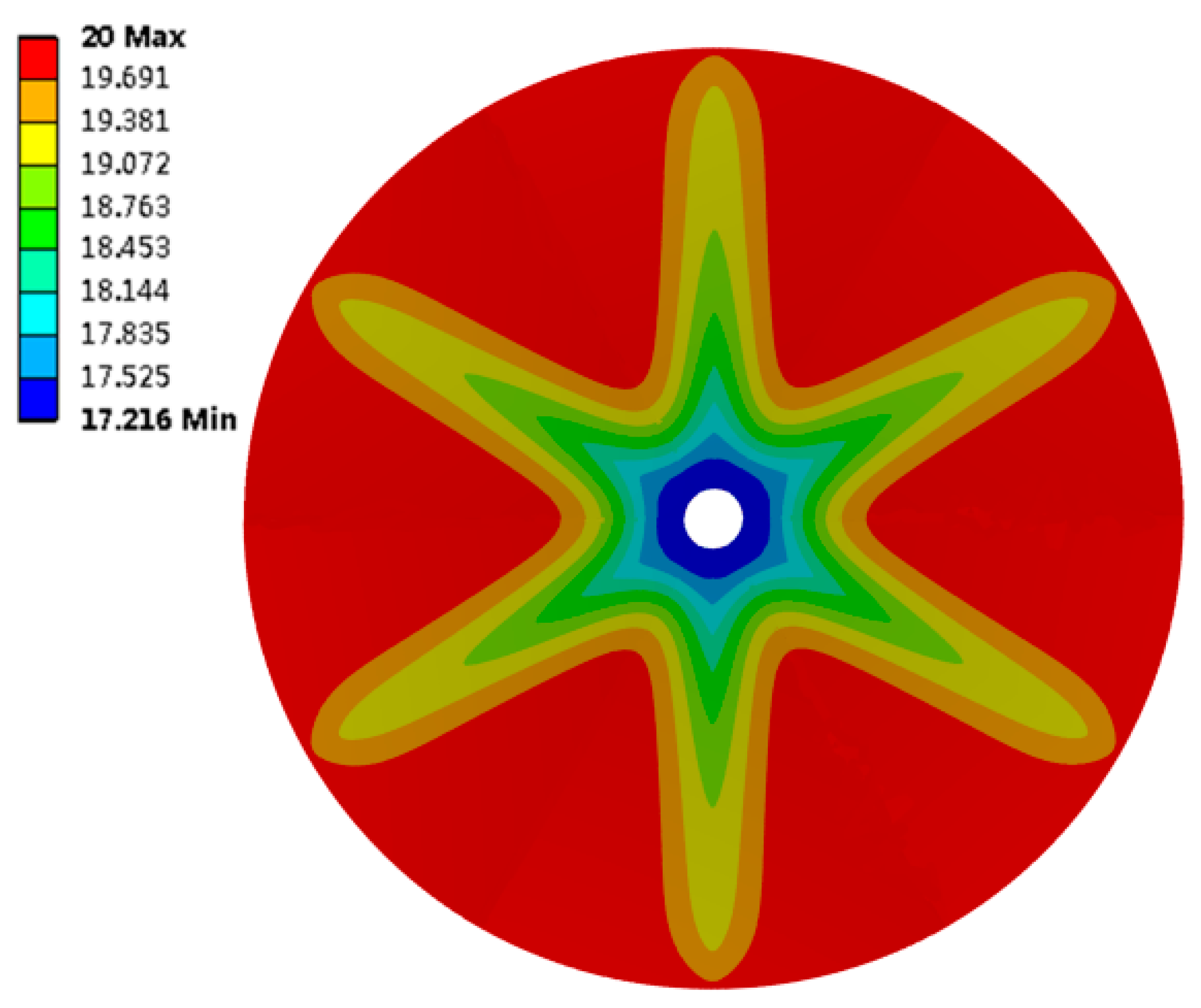
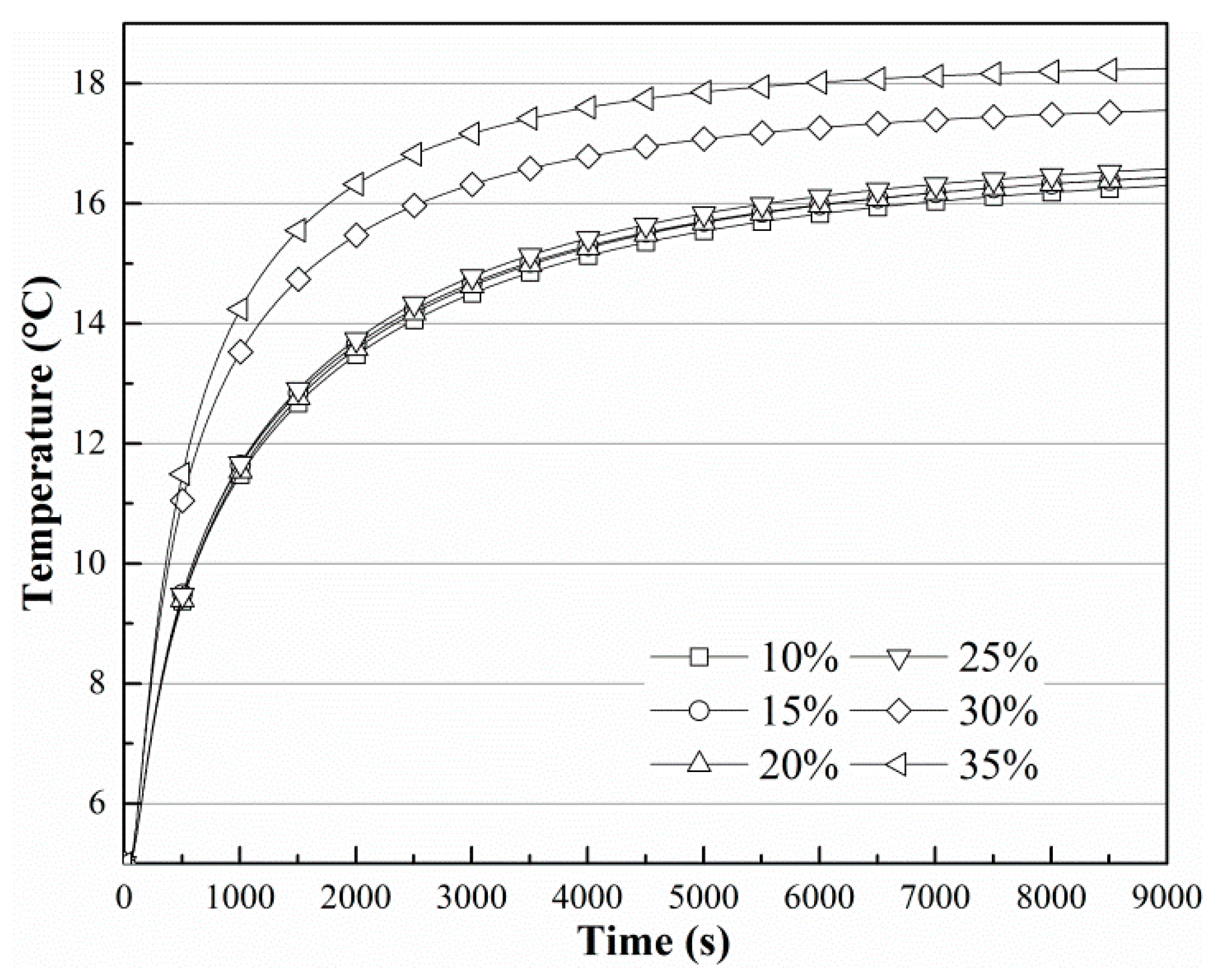
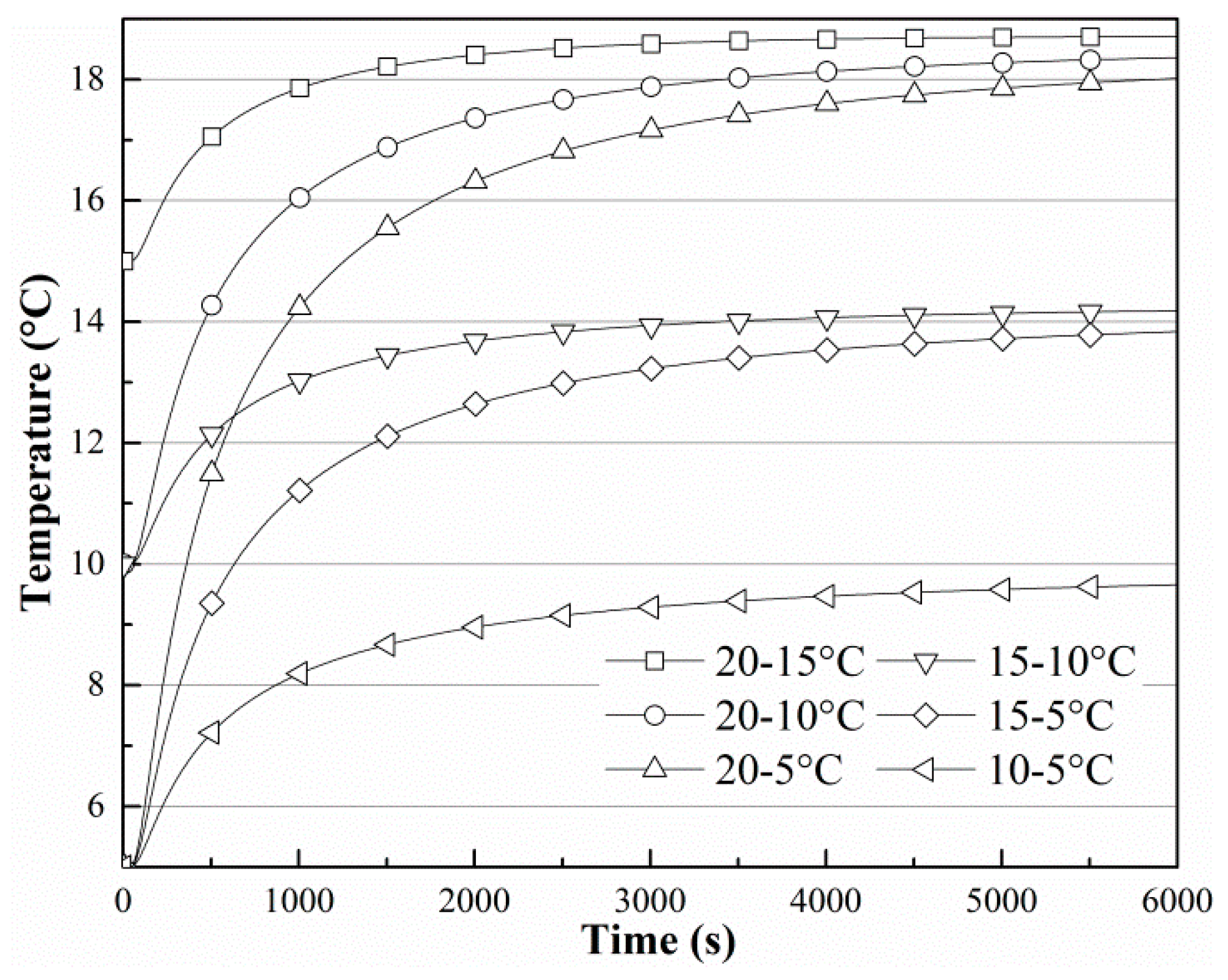
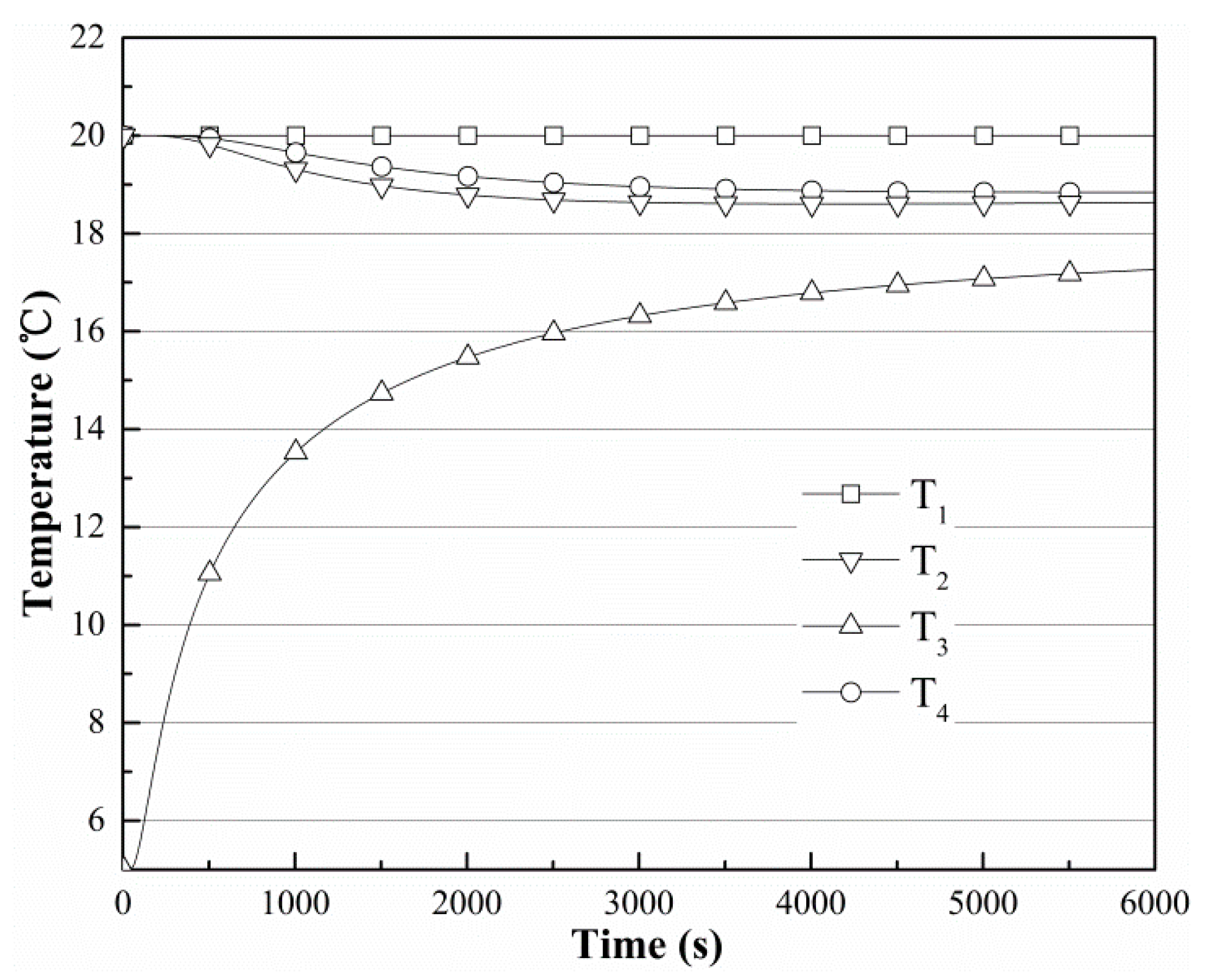
3. Results and Discussion
- (1)
- The material of the finned tube is aluminium in Demir’s work and polyethylene in Bouhacina’s, whereas it is copper in this work. The thermo-physical properties of copper are better than those of either aluminium or polyethylene;
- (2)
- The fin length is 150 mm in Demir’s work, whereas it is 250 mm in this work. The area of the contact region is the smallest in Bouhacina’s internal finned tube;
- (3)
- The moisture levels for soil are 15% in Demir’s work and 35% in this work, and a higher soil moisture content is associated with better thermal conductivity.
4. Conclusions
- (1)
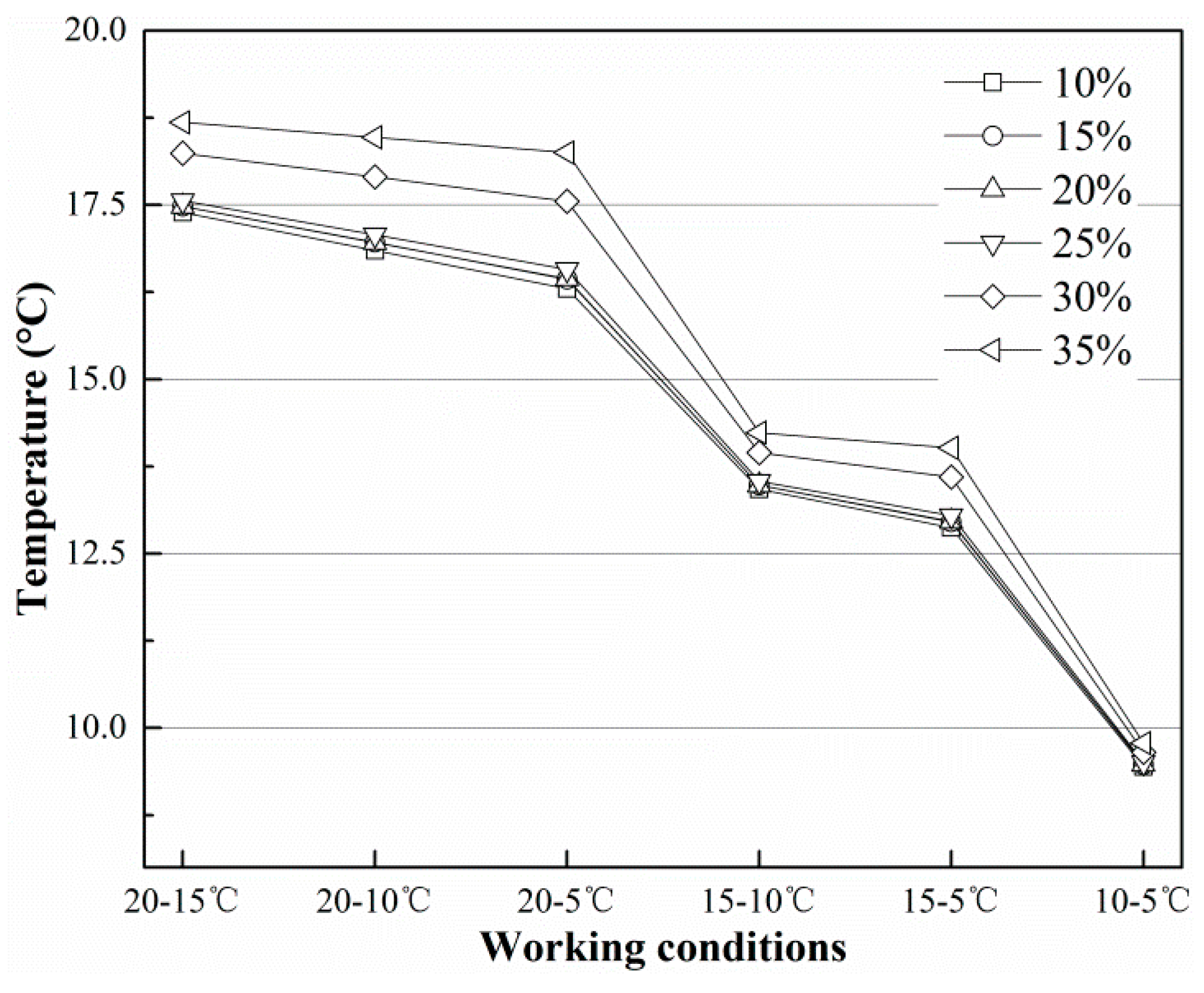
- The performance of the finned tube is considerably better when the soil moisture content reaches 30%, so any device which harvests heat from shallow soil should be placed where the soil moisture content is greater than 30%; under this circumstance the heat transfer can reach an equilibrium state in 6000 s.
- (2)
- The temperature and heat flux are mainly influenced by soil temperature, soil moisture content and the initial temperature of the finned tube.
- (3)
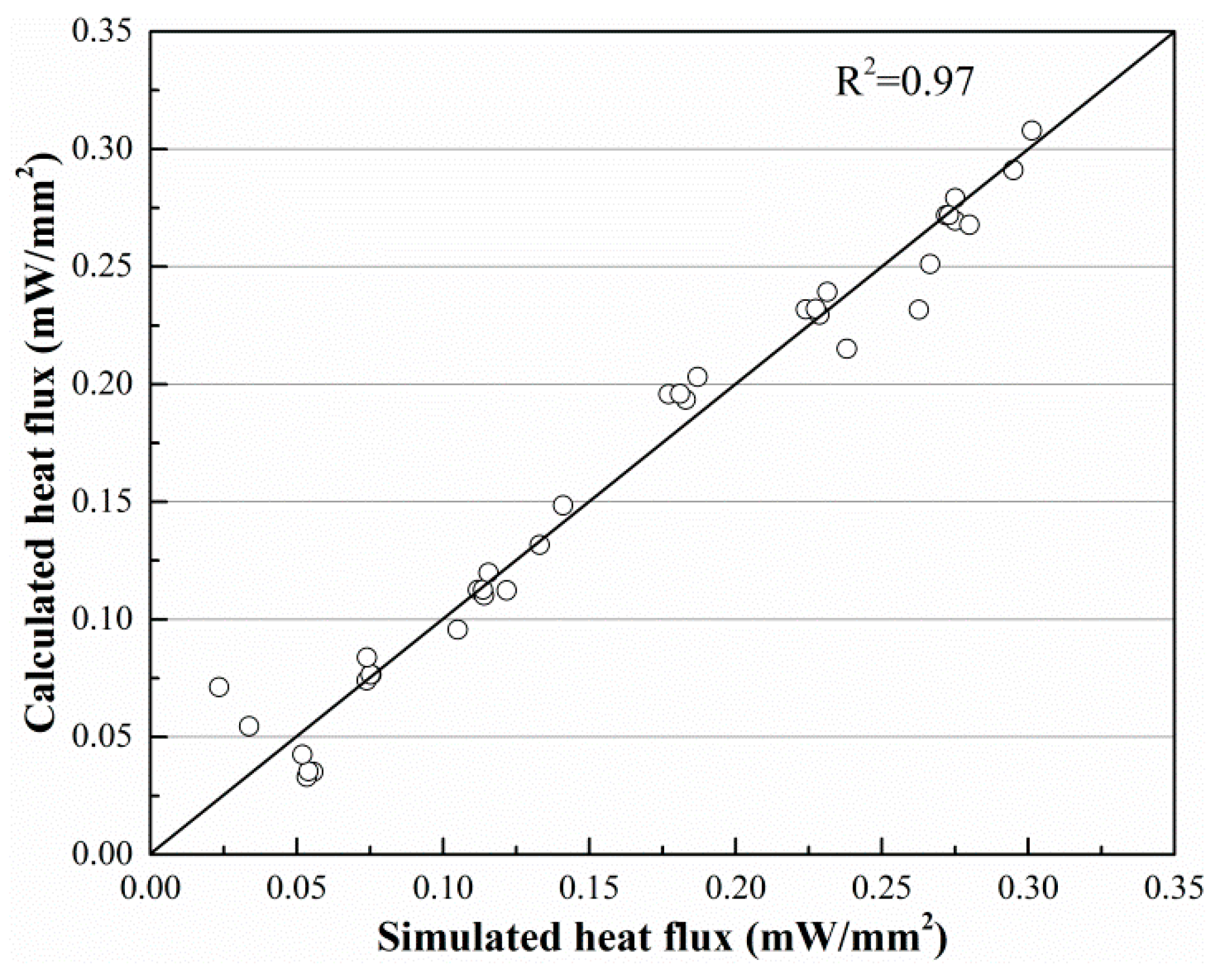
- Simulations show that the highest heat flux can reach approximately 0.30 mW/mm2, and approximately 1507.96 mW of energy can be harvested through the finned tube. A comparison of the simulation and theoretical calculation data shows that the heat transfer rate for this finned tube is 76.77% higher than that of the bare tube if the material is copper.
- (4)
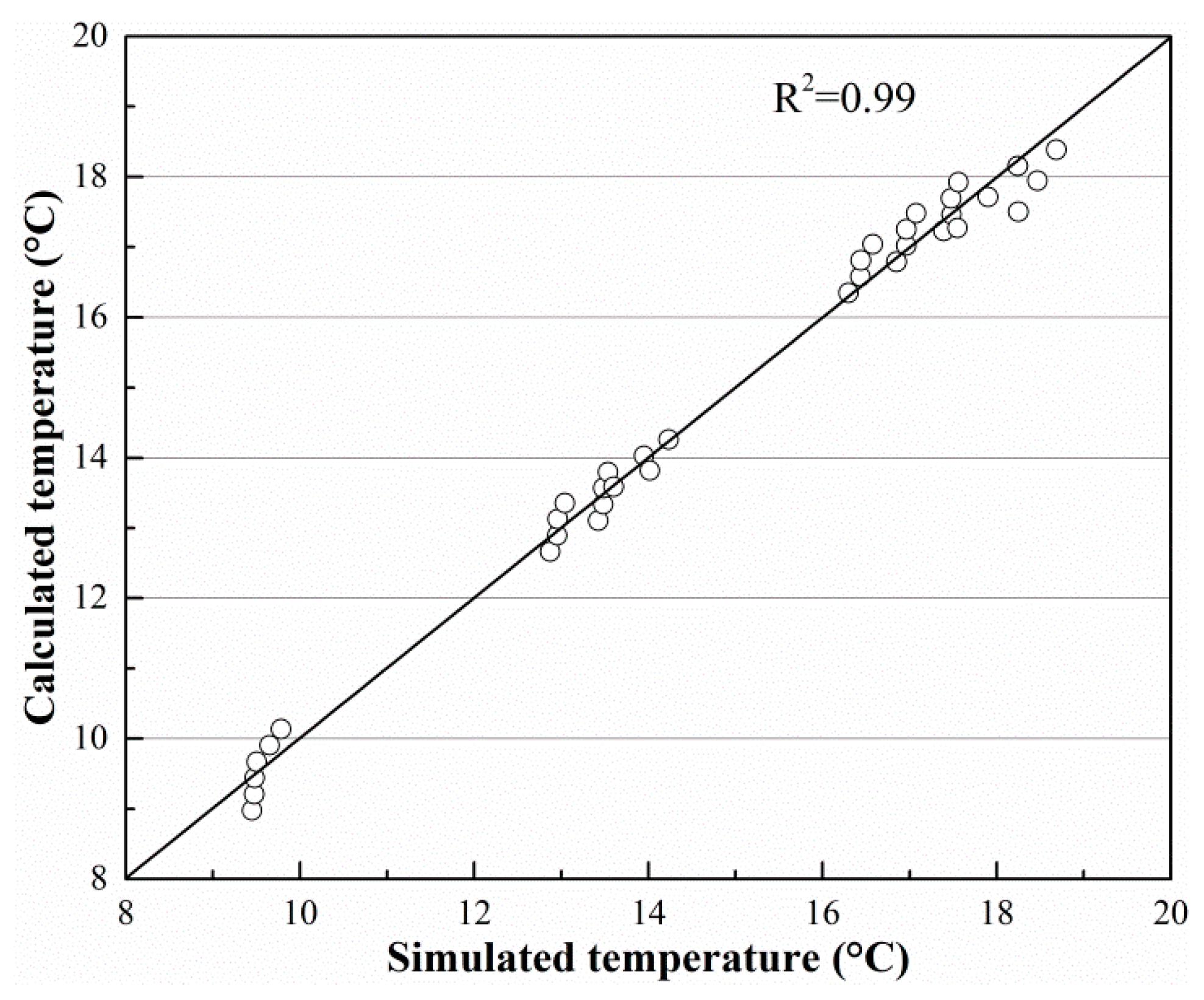
- Two empirical formulas are obtained from the simulation data, and the temperature on the inside of the finned tube and the heat flux absorbed by the finned tube can be obtained using these formulas. The goodness of fit of those two empirical formulas is greater than 97%.
- (5)
- A set of thermoelectric power generation devices was buried in a suburb of Harbin City, and a field experiment was carried out for nine months, where the temperature was continuously observed. The results show that the field experiment data are consistent with the calculated data, and thus, the field test verified the theoretical analysis.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Ti | temperature probes |
| Ts | temperature of soil |
| Tf | temperature of finned tube |
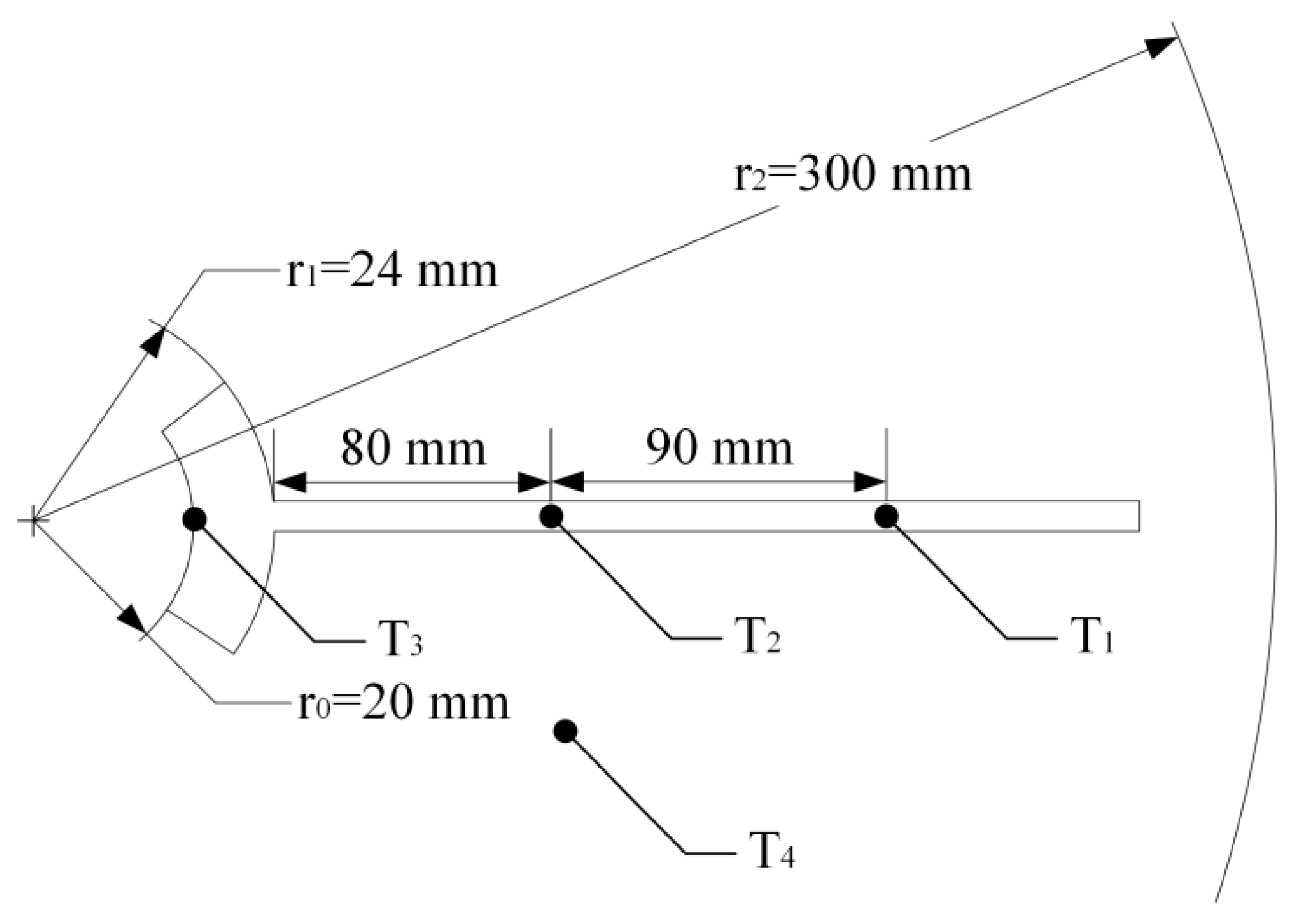
| r0 | inner radius of copper tube |
| r1 | outer radius of copper tube |
| r2 | radius of 2-D model |
| r | radius |
| density of soil | |
| c | specific heat of soil |
| T | temperature |
| time | |
| λ | thermal conductivity of soil |
| qv | heat produced by soil |
| Ta | temperature on r1 |
| Tb | temperature on r2 |
| q | heat flux |
| Φ | heat flow |
| L | length |
| R2 | goodness of fit |
References
- Stevens, J.W. Performance factors for ground-air thermoelectric power generators. Energy Convers. Manag. 2013, 68, 114–123. [Google Scholar] [CrossRef]
- Lawrence, E.E.; Snyder, G.J. A study of heat sink performance in air and soil for use in a thermoelectric energy harvesting device. In Proceedings of the Twenty-First International Conference on Thermoelectrics, Long Beach, CA, USA, 29 August 2002; pp. 446–449. [Google Scholar]
- Zhang, Z.; Li, W.; Kan, J. Behavior of a thermoelectric power generation device based on solar irradiation and the earth’s surface-air temperature difference. Energy Convers. Manag. 2015, 97, 178–187. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, W.; Kan, J.; Xu, D. Theoretical and experimental analysis of a solar thermoelectric power generation device based on gravity-assisted heat pipes and solar irradiation. Energy Convers. Manag. 2016, 127, 301–311. [Google Scholar] [CrossRef]
- Nuwayhid, R.Y.; Shihadeh, A.; Ghaddar, N. Development and testing of a domestic woodstove thermoelectric generator with natural convection cooling. Energy Convers. Manag. 2005, 46, 1631–1643. [Google Scholar] [CrossRef]
- Huang, Y.S.; Xu, D.C.; Li, W.B.; Zhang, B.W. Study on forest soil thermoelectric power generation based on the Seebeck effect. J. For. Environ. 2018, 38, 84–90. [Google Scholar]
- Wang, N.; Xu, D.; Li, W.; Chen, C.; Huang, Y. Feasibility study of a new thermoelectric conversion device utilizing the temperature differences in forest soil. Acta Tech. CSAV (Ceskoslovensk Akad. Ved) 2017, 62, 1–12. [Google Scholar]
- Khalajzadeh, V.; Heidarinejad, G.; Srebric, J. Parameters optimization of a vertical ground heat exchanger based on response surface methodology. Energy Build. 2011, 43, 1288–1294. [Google Scholar] [CrossRef]
- Demir, H.; Koyun, A.; Atayilmaz, Ş.Ö.; Aǧra, Ö.; Dalkiliç, A.S. Investigation of the effects of geometrical parameters on heat transfer from buried finned pipes. J. Mech. Sci. Technol. 2013, 27, 2497–2506. [Google Scholar] [CrossRef]
- Kayaci, N.; Demir, H. Numerical modelling of transient soil temperature distribution for horizontal ground heat exchanger of ground source heat pump. Geothermics 2018, 73, 33–47. [Google Scholar] [CrossRef]
- Beier, R.A. Transient heat transfer in a U-tube borehole heat exchanger. Appl. Therm. Eng. 2014, 62, 256–266. [Google Scholar] [CrossRef]
- Rouag, A.; Benchabane, A.; Mehdid, C.E. Thermal design of Earth-to-Air Heat Exchanger. Part I a new transient semi-analytical model for determining soil temperature. J. Clean. Prod. 2018, 182, 538–544. [Google Scholar] [CrossRef]
- Li, S.; Yang, W.; Zhang, X. Soil temperature distribution around a U-tube heat exchanger in a multi-function ground source heat pump system. Appl. Therm. Eng. 2009, 29, 3679–3686. [Google Scholar] [CrossRef]
- Qi, D.; Pu, L.; Sun, F.; Li, Y. Numerical investigation on thermal performance of ground heat exchangers using phase change materials as grout for ground source heat pump system. Appl. Therm. Eng. 2016, 106, 1023–1032. [Google Scholar] [CrossRef]
- Borinaga-Treviño, R.; Pascual-Muñoz, P.; Castro-Fresno, D.; Blanco-Fernandez, E. Borehole thermal response and thermal resistance of four different grouting materials measured with a TRT. Appl. Therm. Eng. 2013, 53, 13–20. [Google Scholar] [CrossRef]
- Chen, J.; Xia, L.; Li, B.; Mmereki, D. Simulation and experimental analysis of optimal buried depth of the vertical U-tube ground heat exchanger for a ground-coupled heat pump system. Renew. Energy 2015, 73, 46–54. [Google Scholar] [CrossRef]
- Bouhacina, B.; Saim, R.; Oztop, H.F. Numerical investigation of a novel tube design for the geothermal borehole heat exchanger. Appl. Therm. Eng. 2015, 79, 153–162. [Google Scholar] [CrossRef]
- Orr, B.; Akbarzadeh, A.; Lappas, A. An exhaust heat recovery system utilising thermoelectric generators and heat pipes. Appl. Therm. Eng. 2017, 126, 1185–1190. [Google Scholar] [CrossRef]
- Najjar, Y.S.H.; Kseibi, M. Evaluation of experimental JUST thermoelectric stove for electricity- Deprived regions. Renew. Sustain. Energy Rev. 2017, 69, 854–861. [Google Scholar] [CrossRef]
- Liu, T.; Wang, T.; Luan, W.; Cao, Q. Optimal Number of Thermoelectric Couples in a Heat Pipe Assisted Thermoelectric Generator for Waste Heat Recovery. J. Electron. Mater. 2017, 46, 3137–3144. [Google Scholar] [CrossRef]
- Thielen, M.; Sigrist, L.; Magno, M.; Hierold, C.; Benini, L. Human body heat for powering wearable devices: From thermal energy to application. Energy Convers. Manag. 2017, 131, 44–54. [Google Scholar] [CrossRef]
- Maixner, M.R.; Stevens, J.W. Assessment of near-surface ground temperature profiles for optimal placement of a thermoelectric device. Energy Convers. Manag. 2009, 50, 2361–2365. [Google Scholar] [CrossRef]
- Yang, W.; Liang, X.; Shi, M.; Chen, Z. A Numerical Model for the Simulation of a Vertical U-Bend Ground Heat Exchanger Used in a Ground-Coupled Heat Pump. Int. J. Green Energy 2014, 11, 761–785. [Google Scholar] [CrossRef]
- Koyun, A.; Demir, H.; Torun, Z. Experimental study of heat transfer of buried finned pipe for ground source heat pump applications. Int. Commun. Heat Mass Transf. 2009, 36, 739–743. [Google Scholar] [CrossRef]
- Jahangir, M.H.; Sarrafha, H.; Kasaeian, A. Numerical modeling of energy transfer in underground borehole heat exchanger within unsaturated soil. Appl. Therm. Eng. 2018, 132, 697–707. [Google Scholar] [CrossRef]
- Yavuzturk, C.; Spitler, J.D. A short time step response factor model for vertical ground loop heat exchangers. ASHRAE Trans. 1999, 105, 475–485. [Google Scholar]
- Agrawal, K.K.; Misra, R.; Yadav, T.; Agrawal, G.D.; Jamuwa, D.K. Experimental study to investigate the effect of water impregnation on thermal performance of earth air tunnel heat exchanger for summer cooling in hot and arid climate. Renew. Energy 2018, 120, 255–265. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, W. Heat Engineering; Higher Education Press: Beijing, China, 2004. [Google Scholar]



| Moisture % | Thermal Conductivity W m−1 K−1 | Specific Heat J kg−1 K−1 | Density kg m−3 |
|---|---|---|---|
| 10 | 0.3624 | 731.9 | 1184.9 |
| 15 | 0.3885 | 736.7 | 1178.1 |
| 20 | 0.4125 | 632.4 | 1051.6 |
| 25 | 0.4513 | 601.5 | 1066.7 |
| 30 | 0.6025 | 1329.4 | 1033.5 |
| 35 | 1.2731 | 659.1 | 849.3 |
| Ts °C | Tf °C | Moisture Content (M) % | T3 (°C) | Heat Flux (mW/mm2) | ||
|---|---|---|---|---|---|---|
| Simulated | Calculated | Simulated | Calculated | |||
| 20 | 15 | 10 | 17.39 | 17.23 | 0.27 | 0.27 |
| 20 | 10 | 10 | 16.85 | 16.79 | 0.22 | 0.23 |
| 20 | 5 | 10 | 16.30 | 16.35 | 0.18 | 0.20 |
| 15 | 10 | 10 | 13.43 | 13.10 | 0.11 | 0.11 |
| 15 | 5 | 10 | 12.87 | 12.66 | 0.08 | 0.08 |
| 10 | 5 | 10 | 9.45 | 8.98 | 0.06 | 0.04 |
| 20 | 15 | 15 | 17.48 | 17.46 | 0.28 | 0.27 |
| 20 | 10 | 15 | 16.96 | 17.02 | 0.23 | 0.23 |
| 20 | 5 | 15 | 16.44 | 16.58 | 0.18 | 0.19 |
| 15 | 10 | 15 | 13.48 | 13.34 | 0.11 | 0.11 |
| 15 | 5 | 15 | 12.95 | 12.90 | 0.07 | 0.07 |
| 10 | 5 | 15 | 9.47 | 9.21 | 0.05 | 0.03 |
| 20 | 15 | 20 | 17.48 | 17.69 | 0.27 | 0.27 |
| 20 | 10 | 20 | 16.96 | 17.25 | 0.23 | 0.23 |
| 20 | 5 | 20 | 16.44 | 16.81 | 0.18 | 0.20 |
| 15 | 10 | 20 | 13.48 | 13.57 | 0.11 | 0.11 |
| 15 | 5 | 20 | 12.96 | 13.13 | 0.08 | 0.08 |
| 10 | 5 | 20 | 9.48 | 9.44 | 0.05 | 0.04 |
| 20 | 15 | 25 | 17.56 | 17.92 | 0.28 | 0.28 |
| 20 | 10 | 25 | 17.07 | 17.48 | 0.23 | 0.24 |
| 20 | 5 | 25 | 16.58 | 17.04 | 0.19 | 0.20 |
| 15 | 10 | 25 | 13.54 | 13.80 | 0.12 | 0.12 |
| 15 | 5 | 25 | 13.04 | 13.36 | 0.07 | 0.08 |
| 10 | 5 | 25 | 9.50 | 9.67 | 0.05 | 0.04 |
| 20 | 15 | 30 | 18.24 | 18.16 | 0.30 | 0.29 |
| 20 | 10 | 30 | 17.90 | 17.71 | 0.27 | 0.25 |
| 20 | 5 | 30 | 17.55 | 17.27 | 0.24 | 0.22 |
| 15 | 10 | 30 | 13.95 | 14.03 | 0.13 | 0.13 |
| 15 | 5 | 30 | 13.60 | 13.59 | 0.11 | 0.10 |
| 10 | 5 | 30 | 9.65 | 9.90 | 0.03 | 0.05 |
| 20 | 15 | 35 | 18.68 | 18.39 | 0.30 | 0.31 |
| 20 | 10 | 35 | 18.47 | 17.95 | 0.28 | 0.27 |
| 20 | 5 | 35 | 18.25 | 17.50 | 0.26 | 0.23 |
| 15 | 10 | 35 | 14.24 | 14.26 | 0.14 | 0.15 |
| 15 | 5 | 35 | 14.02 | 13.82 | 0.12 | 0.11 |
| 10 | 5 | 35 | 9.78 | 10.14 | 0.02 | 0.07 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Li, W.; Xu, D.; Wu, Y. Spatiotemporal Rule of Heat Transfer on a Soil/Finned Tube Interface. Sensors 2019, 19, 1159. https://doi.org/10.3390/s19051159
Huang Y, Li W, Xu D, Wu Y. Spatiotemporal Rule of Heat Transfer on a Soil/Finned Tube Interface. Sensors. 2019; 19(5):1159. https://doi.org/10.3390/s19051159
Chicago/Turabian StyleHuang, Yongsheng, Wenbin Li, Daochun Xu, and Yafeng Wu. 2019. "Spatiotemporal Rule of Heat Transfer on a Soil/Finned Tube Interface" Sensors 19, no. 5: 1159. https://doi.org/10.3390/s19051159
APA StyleHuang, Y., Li, W., Xu, D., & Wu, Y. (2019). Spatiotemporal Rule of Heat Transfer on a Soil/Finned Tube Interface. Sensors, 19(5), 1159. https://doi.org/10.3390/s19051159




