UAV Landing Based on the Optical Flow Videonavigation
Abstract
:1. Introduction
- the tracking of singular points and development of the algorithm based on determining of their angular coordinates and establishing of correspondence of their images in preliminary uploaded template map based on RANSAC methodology described in [5];
- conjugation of the rectilinear objects segments such as walls of buildings and roads are in [6];
- fitting of characteristic curvilinear elements [7];
- matching of epipolar lines, such as runways, at landing [10].
- in landing at the unknown hazardous environment with the choice of the landing place [17];
- in experimental landing with the aid of special landing pads [18];
- vision based and mapping for landing with the aid of model predictive control [19];
- in tracking tasks of linear objects such as communication lines and pipelines on the terrain [22];
- even in usual manoeuvring [23];
- slope estimation for autonomous landing [24];
- in distance estimation with application to the UAV landing with the aid of the mono camera [25].
2. OF Computation: Theory
3. Estimation of the UAV Motion by the OF and the Kalman Filtering
3.1. The UAV Linear Velocity Estimation
- —the vector of accelerations coming from INS (inertial navigation system),
- —is the vector of the current perturbations in UAV motion.We assume that the components of the perturbation vector are white noises with variances
3.2. The UAV Angles and Angular Velocities Estimation
3.3. Joint Estimation of the UAV Attitude
3.4. Discussion of the Algorithm
4. OF Estimation in the Real Flight
4.1. Examples of the OF Estimation in Approaching to the Earth
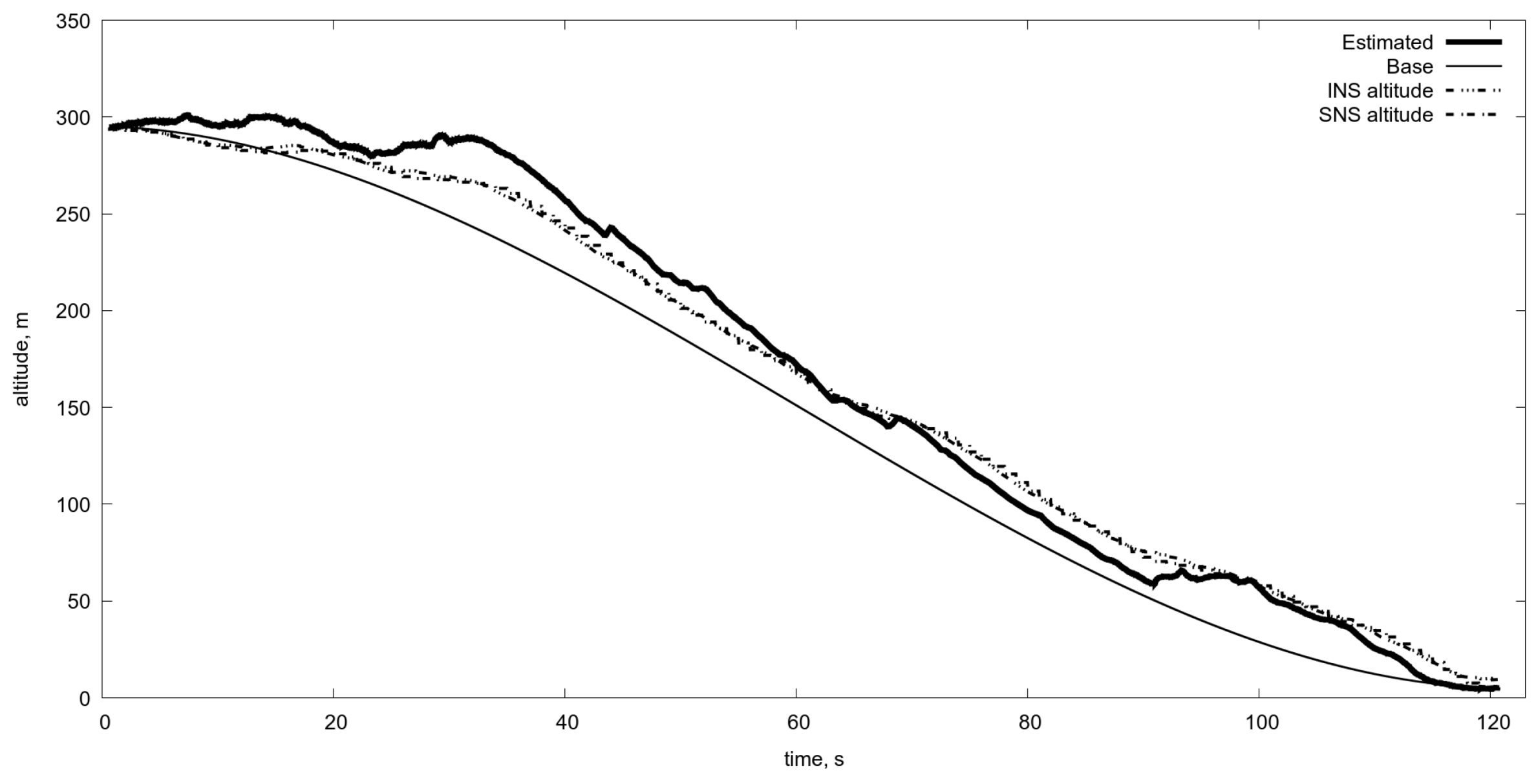
4.2. Switching of Scaling by Means of the Altitude Estimation
4.3. Test of the Algorithm Based on the Scale Switching via Current Altitude Estimation
5. Scale Switching by the Comparison of Calculated and Estimated OF
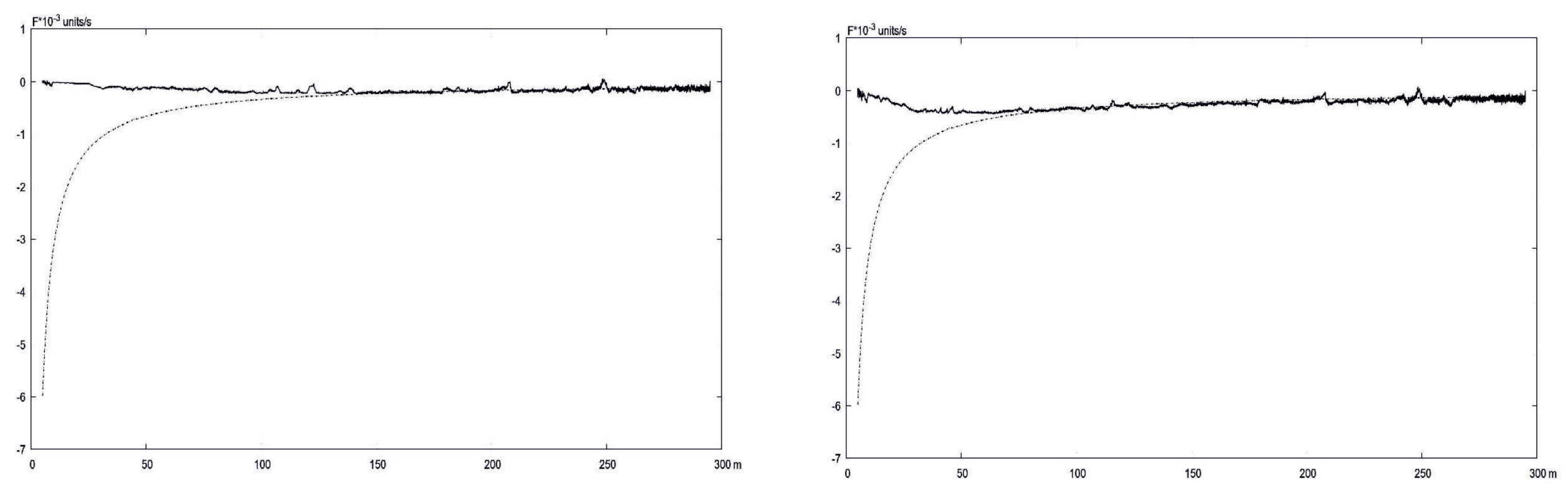
5.1. Comparison of Calculated and Estimated OF
5.2. OF Estimation as a Sensor for Scaling Switch
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| UAV | Unmanned Aerial Vehicle |
| INS | Inertial navigation system |
| SNS | Satellite navigation system |
| OF | Optical flow |
| LHS | Left hand side |
| RHS | Right hand side |
| L–K | Lucas–Kanade (algorithm) |
| OES | Optoelectronic system |
References
- Aggarwal, J.; Nandhakumar, N. On the computation of motion from sequences of images—A review. Proc. IEEE 1988, 76, 917–935. [Google Scholar] [CrossRef]
- Konovalenko, I.; Kuznetsova, E.; Miller, A.; Miller, B.; Popov, A.; Shepelev, D.; Stepanyan, K. New Approaches to the Integration of Navigation Systems for Autonomous Unmanned Vehicles (UAV). Sensors 2018, 18, 3010. [Google Scholar] [CrossRef] [PubMed]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; Volume 2, pp. 1150–1157. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Karpenko, S.; Konovalenko, I.; Miller, A.; Miller, B.; Nikolaev, D. UAV Control on the Basis of 3D Landmark Bearing-Only Observations. Sensors 2015, 15, 29802–29820. [Google Scholar] [CrossRef]
- Kunina, I.; Terekhin, A.; Khanipov, T.; Kuznetsova, E.; Nikolaev, D. Aerial image geolocalization by matching its line structure with route map. In Proceedings of the Ninth International Conference on Machine Vision (ICMV 2016), Nice, France, 17 March 2017; Volume 10341. [Google Scholar]
- Savchik, A.V.; Sablina, V.A. Finding the correspondence between closed curves under projective distortions. Sens. Syst. 2018, 32, 60–66. (In Russian) [Google Scholar] [CrossRef]
- Kunina, I.; Teplyakov, L.; Gladkov, A.; Khanipov, T.; Nikolaev, D. Aerial images visual localization on a vector map using color-texture segmentation. In Proceedings of the Tenth International Conference on Machine Vision (ICMV 2017), Vienna, Austria, 13–15 November 2017; Volume 10696. [Google Scholar]
- Teplyakov, L.; Kunina, I.A.; Gladkov, A. Visual localisation of aerial images on vector map using colour-texture segmentation. Sens. Syst. 2018, 32, 26–34. (In Russian) [Google Scholar] [CrossRef]
- Ovchinkin, A.; Ershov, E. The algorithm of epipole position estimation under pure camera translation. Sens. Syst. 2018, 32, 42–49. (In Russian) [Google Scholar] [CrossRef]
- Cesetti, A.; Frontoni, E.; Mancini, A.; Zingaretti, P.; Longhi, S. A Vision-Based Guidance System for UAV Navigation and Safe Landing using Natural Landmarks. J. Intell. Robot. Syst. 2010, 57, 233. [Google Scholar] [CrossRef]
- Sebesta, K.; Baillieul, J. Animal-inspired agile flight using optical flow sensing. In Proceedings of the 2012 IEEE 51st Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 3727–3734. [Google Scholar] [CrossRef]
- Miller, B.M.; Fedchenko, G.I.; Morskova, M.N. Computation of the image motion shift at panoramic photography. Izvestia Vuzov. Geod. Aerophotogr. 1984, 4, 81–89. (In Russian) [Google Scholar]
- Miller, B.M.; Fedchenko, G.I. Effect of the attitude errors on image motion shift at photography from moving aircraft. Izvestia Vuzov. Geod. Aerophotogr. 1984, 5, 75–80. (In Russian) [Google Scholar]
- Miller, B.; Rubinovich, E. Image motion compensation at charge-coupled device photographing in delay-integration mode. Autom. Remote Control 2007, 68, 564–571. [Google Scholar] [CrossRef]
- Kistlerov, V.; Kitsul, P.; Miller, B. Computer-aided design of the optical devices control systems based on the language of algebraic computations FLAC. Math. Comput. Simul. 1991, 33, 303–307. [Google Scholar] [CrossRef]
- Johnson, A.; Montgomery, J.; Matthies, L. Vision Guided Landing of an Autonomous Helicopter in Hazardous Terrain. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 3966–3971. [Google Scholar] [CrossRef]
- Merz, T.; Duranti, S.; Conte, G. Autonomous Landing of an Unmanned Helicopter based on Vision and Inertial Sensing. In Experimental Robotics IX; Ang, M.H., Khatib, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 343–352. ISBN 978-3-540-28816-9. [Google Scholar]
- Templeton, T.; Shim, D.H.; Geyer, C.; Sastry, S.S. Autonomous Vision-based Landing and Terrain Mapping Using an MPC-controlled Unmanned Rotorcraft. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 1349–1356. [Google Scholar] [CrossRef]
- Serra, P.; Le Bras, F.; Hamel, T.; Silvestre, C.; Cunha, R. Nonlinear IBVS controller for the flare maneuver of fixed-wing aircraft using optical flow. In Proceedings of the 49th IEEE Conference on Decision and Control, Atlanta, GA, USA, 15–17 December 2010; pp. 1656–1661. [Google Scholar] [CrossRef]
- McCarthy, C.; Barnes, N. A Unified Strategy for Landing and Docking Using Spherical Flow Divergence. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1024–1031. [Google Scholar] [CrossRef] [PubMed]
- Serra, P.; Cunha, R.; Silvestre, C.; Hamel, T. Visual servo aircraft control for tracking parallel curves. In Proceedings of the 2012 IEEE 51st Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 1148–1153. [Google Scholar] [CrossRef]
- Liau, Y.S.; Zhang, Q.; Li, Y.; Ge, S.S. Non-metric navigation for mobile robot using optical flow. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura, Portugal, 7–12 October 2012; pp. 4953–4958. [Google Scholar] [CrossRef]
- De Croon, G.; Ho, H.; Wagter, C.; van Kampen, E.; Remes, B.; Chu, Q. Optic-Flow Based Slope Estimation for Autonomous Landing. Int. J. Micro Air Veh. 2013, 5, 287–297. [Google Scholar] [CrossRef]
- De Croon, G.C.H.E. Monocular distance estimation with optical flow maneuvers and efference copies: a stability-based strategy. Bioinspir. Biomim. 2016, 11, 016004. [Google Scholar] [CrossRef]
- Rosa, L.; Hamel, T.; Mahony, R.; Samson, C. Optical-Flow Based Strategies for Landing VTOL UAVs in Cluttered Environments. IFAC Proc. Vol. 2014, 47, 3176–3183. [Google Scholar] [CrossRef]
- Horn, B.K.P.; Schunck, B.G. Determining Optical Flow. Artif. Intell. 1981, 17, 185–203. [Google Scholar] [CrossRef]
- Herissé, B.; Hamel, T.; Mahony, R.; Russotto, F. Landing a VTOL Unmanned Aerial Vehicle on a Moving Platform Using Optical Flow. IEEE Trans. Robot. 2012, 28, 77–89. [Google Scholar] [CrossRef]
- Pijnacker Hordijk, B.J.; Scheper, K.Y.W.; de Croon, G.C.H.E. Vertical landing for micro air vehicles using event-based optical flow. J. Field Robot. 2018, 35, 69–90. [Google Scholar] [CrossRef]
- Ho, H.W.; de Croon, G.C.H.E.; van Kampen, E.; Chu, Q.P.; Mulder, M. Adaptive Control Strategy for Constant Optical Flow Divergence Landing. arXiv, 2016; arXiv:1609.06767. [Google Scholar] [CrossRef]
- Ho, H.W.; de Croon, G.C.H.E.; van Kampen, E.; Chu, Q.P.; Mulder, M. Adaptive Gain Control Strategy for Constant Optical Flow Divergence Landing. IEEE Trans. Robot. 2018, 34, 508–516. [Google Scholar] [CrossRef]
- Fantoni, I.; Sanahuja, G. Optic-Flow Based Control and Navigation of Mini Aerial Vehicles. J. Aerosp. Lab 2014. [Google Scholar] [CrossRef]
- Chahl, J.; Rosser, k.; Mizutani, A. Vertically displaced optical flow sensors to control the landing of a UAV. Proc. SPIE 2011, 7975, 797518. [Google Scholar] [CrossRef]
- Rosser, K.; Fatiaki, A.; Ellis, A.; Mizutani, A.; Chahl, J. Micro-autopilot for research and development. In 16th Australian International Aerospace Congress (AIAC16); Engineers Australia: Melbourne, Australia, 2015; pp. 173–183. [Google Scholar]
- Popov, A.; Miller, A.; Stepanyan, K.; Miller, B. Modelling of the unmanned aerial vehicle navigation on the basis of two height-shifted onboard cameras. Sens. Syst. 2018, 32, 19–25. (In Russian) [Google Scholar] [CrossRef]
- Miller, A.; Miller, B. Stochastic control of light UAV at landing with the aid of bearing-only observations. In Proceedings of the Eighth International Conference on Machine Vision (ICMV 2015), Barcelona, Spain, 19–21 November 2015; Volume 9875. [Google Scholar]
- Lucas, B.D.; Kanade, T. An Iterative Image Registration Technique with an Application to Stereo Vision. In Proceedings of the 7th International Joint Conference on Artificial Intelligence; IJCAI: Vancouver, BC, Canada, 1981; Volume 2, pp. 674–679. [Google Scholar]
- Chao, H.; Gu, Y.; Gross, J.; Guo, G.; Fravolini, M.L.; Napolitano, M.R. A comparative study of optical flow and traditional sensors in UAV navigation. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 3858–3863. [Google Scholar] [CrossRef]
- Popov, A.; Miller, A.; Miller, B.; Stepanyan, K. Optical flow and inertial navigation system fusion in the UAV navigation. In Proceedings of the Unmanned/Unattended Sensors and Sensor Networks XII, Edinburgh, UK, 26–29 September 2016; Volume 9986. [Google Scholar]
- Farnebäck, G. Fast and accurate motion estimation using orientation tensors and parametric motion models. In Proceedings of the 15th International Conference on Pattern Recognition, IPCR-2000, Barcelona, Spain, 3–8 September 2000; Volume 1, pp. 135–139. [Google Scholar] [CrossRef]
- Farnebäck, G. Orientation estimation based on weighted projection onto quadratic polynomials. In Proceedings of the 5th International Fall Workshop, Vision, Modeling, and Visualization, Saarbrücken, Germany, 22–24 November 2000; Max-Planck-Institut für Informatik: Saarbrücken, Germany, 2000; pp. 89–96. [Google Scholar]
- Farnebäck, G. Two-Frame Motion Estimation Based on Polynomial Expansion. In Proceedings of the 13th Scandinavian Conference on Image Analysis, SCIA 2003, Halmstad, Sweden, 29 June–2 July 2003; pp. 363–370. [Google Scholar] [CrossRef]
- Popov, A.; Miller, A.; Miller, B.; Stepanyan, K. Estimation of velocities via optical flow. In Proceedings of the 2016 International Conference on Robotics and Machine Vision, Moscow, Russia, 14–16 September 2016; Volume 10253. [Google Scholar]
- Popov, A.; Miller, B.; Miller, A.; Stepanyan, K. Optical Flow as a Navigation Means for UAVs with Opto-electronic Cameras. In Proceedings of the 56th Israel Annual Conference on Aerospace Sciences, Tel-Aviv and Haifa, Israel, 9–10 March 2016. [Google Scholar]
- Miller, B.M.; Stepanyan, K.V.; Popov, A.K.; Miller, A.B. UAV navigation based on videosequences captured by the onboard video camera. Autom. Remote Control 2017, 78, 2211–2221. [Google Scholar] [CrossRef]
- Miller, A.; Miller, B.; Popov, A.; Stepanyan, K. Optical Flow as a navigation means for UAV. In Proceedings of the 2018 Australian New Zealand Control Conference (ANZCC), Melbourne, Australia, 7–8 December 2018; pp. 302–307. [Google Scholar] [CrossRef]













| Height | Scale | Height of Switch |
|---|---|---|
| 300–50 m | 150 m | |
| 150–80 m | 80 m | |
| 80–50 m | 50 m | |
| 50–5 m | 5 m |
| INS | SNS | Video | |
|---|---|---|---|
| Mean, m | 17.40 | 17.43 | 23.32 |
| Median, m | 19.39 | 19.75 | 23.85 |
| Minimum, m | −3.36 | −4.41 | −1.32 |
| Maximum, m | 30.04 | 31.78 | 46.87 |
| Standard deviation | 9.33 | 10.02 | 11.60 |
| Standard error | 0.12 | 0.13 | 0.15 |
| Final error, m | 4.42 | −1.21 | −0.15 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miller, A.; Miller, B.; Popov, A.; Stepanyan, K. UAV Landing Based on the Optical Flow Videonavigation. Sensors 2019, 19, 1351. https://doi.org/10.3390/s19061351
Miller A, Miller B, Popov A, Stepanyan K. UAV Landing Based on the Optical Flow Videonavigation. Sensors. 2019; 19(6):1351. https://doi.org/10.3390/s19061351
Chicago/Turabian StyleMiller, Alexander, Boris Miller, Alexey Popov, and Karen Stepanyan. 2019. "UAV Landing Based on the Optical Flow Videonavigation" Sensors 19, no. 6: 1351. https://doi.org/10.3390/s19061351
APA StyleMiller, A., Miller, B., Popov, A., & Stepanyan, K. (2019). UAV Landing Based on the Optical Flow Videonavigation. Sensors, 19(6), 1351. https://doi.org/10.3390/s19061351






