Ultrasonic Inspection of Localized Defects in Low-Porosity CFRP
Abstract
:1. Introduction
2. Backscattered Signal Modelling
2.1. Model of Structural Signal
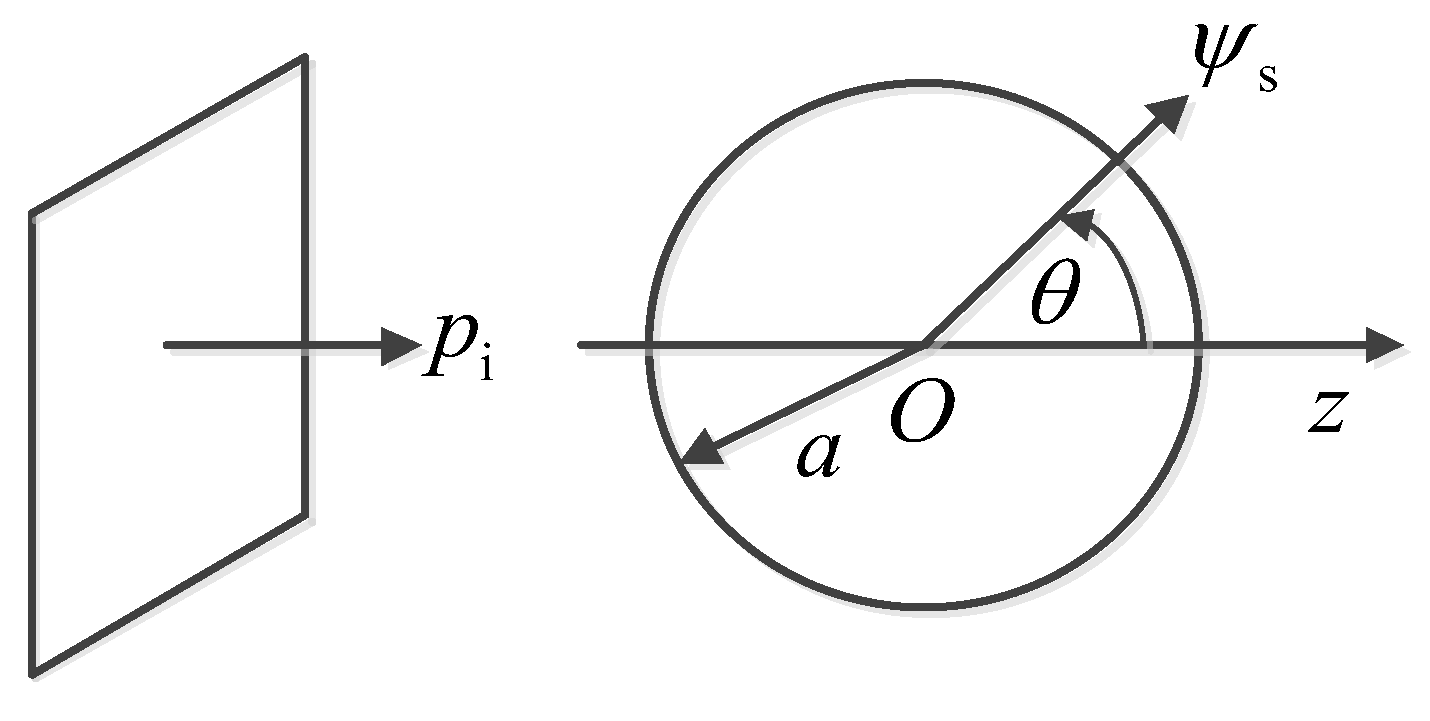
2.2. Model of Scattering Signal
2.3. Model of Non-Acoustic Noise
2.4. Model of Backscattered Signal
3. VMD and GST
3.1. VMD
- Step 1: Initialize .
- Step 2: .
- Step 3: Update and by iterating through .
- Step 4: Update .
- Step 5: For the predefined tolerance , repeat from Step 2 to Step 4 until convergence.
3.2. GST
4. Numeric Simulation
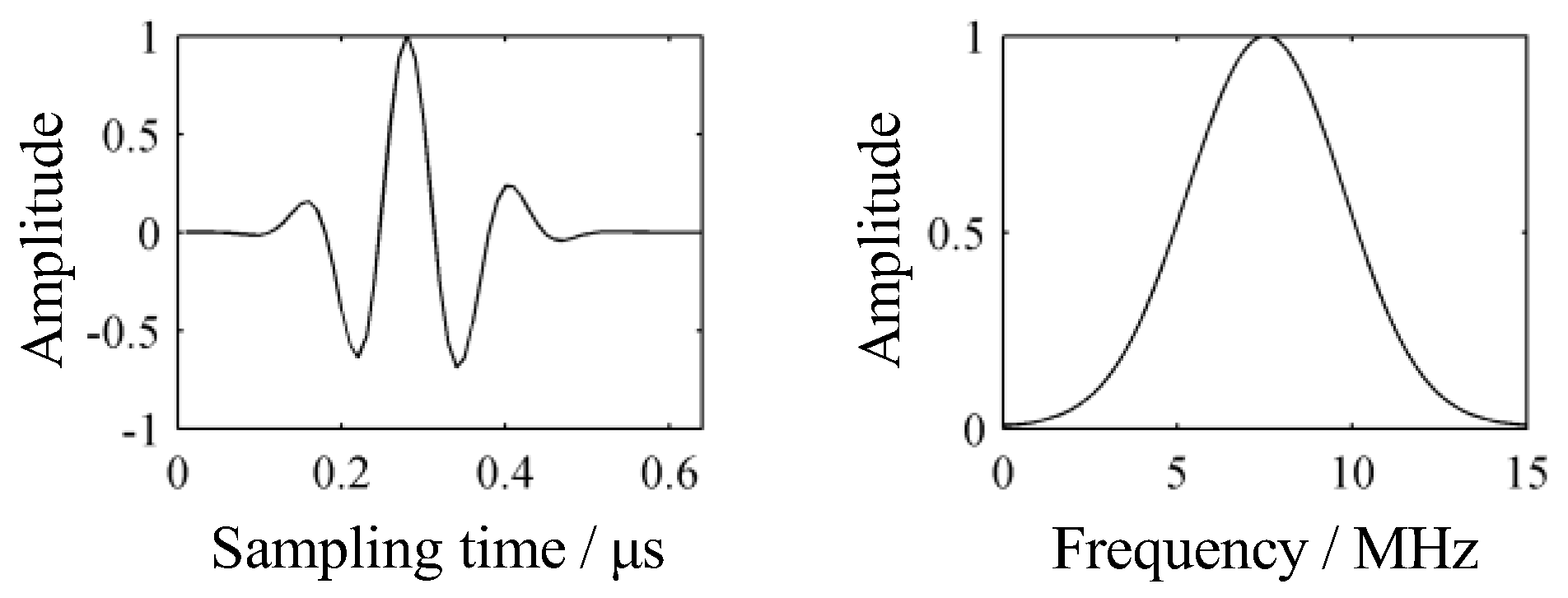
4.1. Parameters Setting in the Simulation
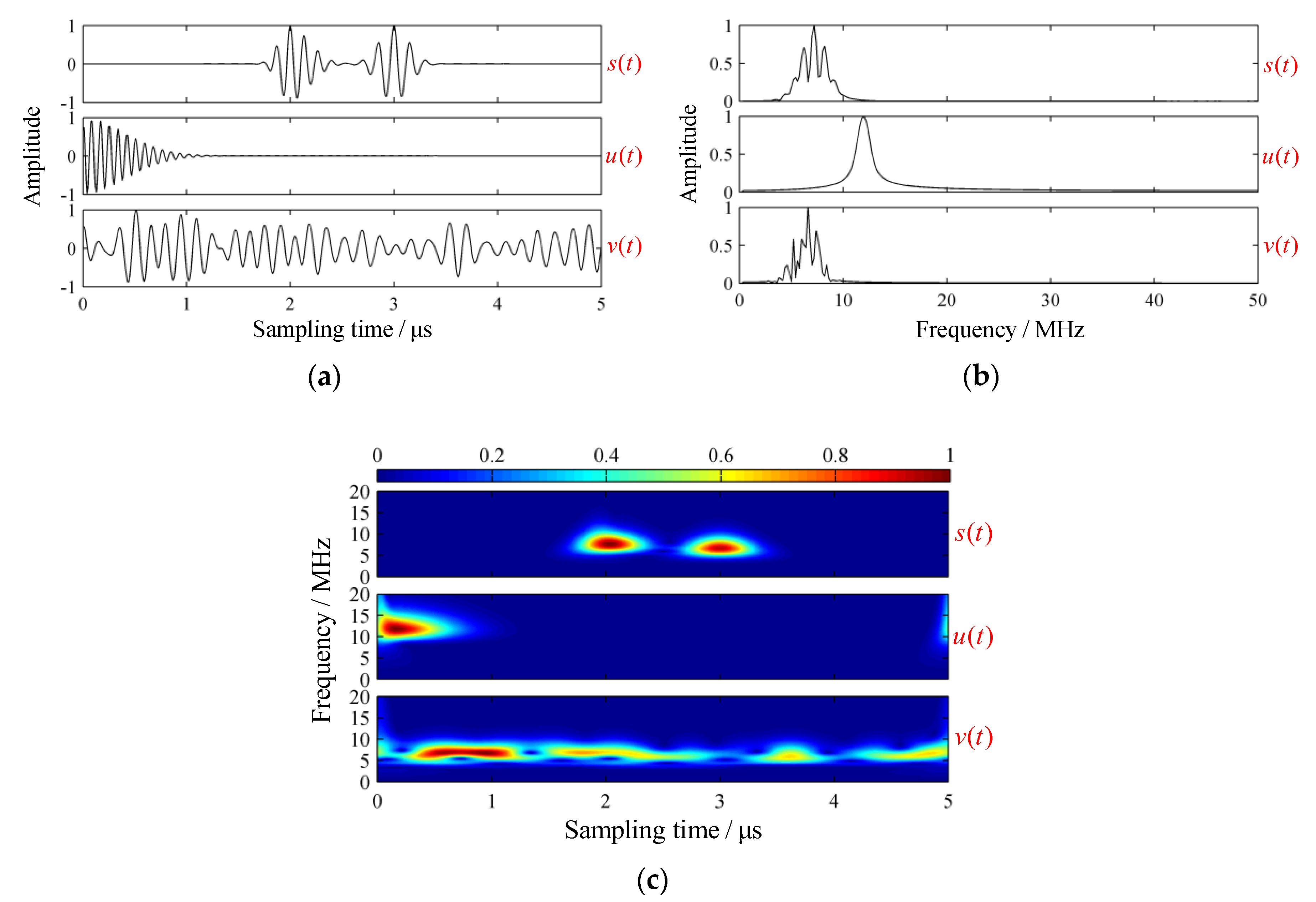
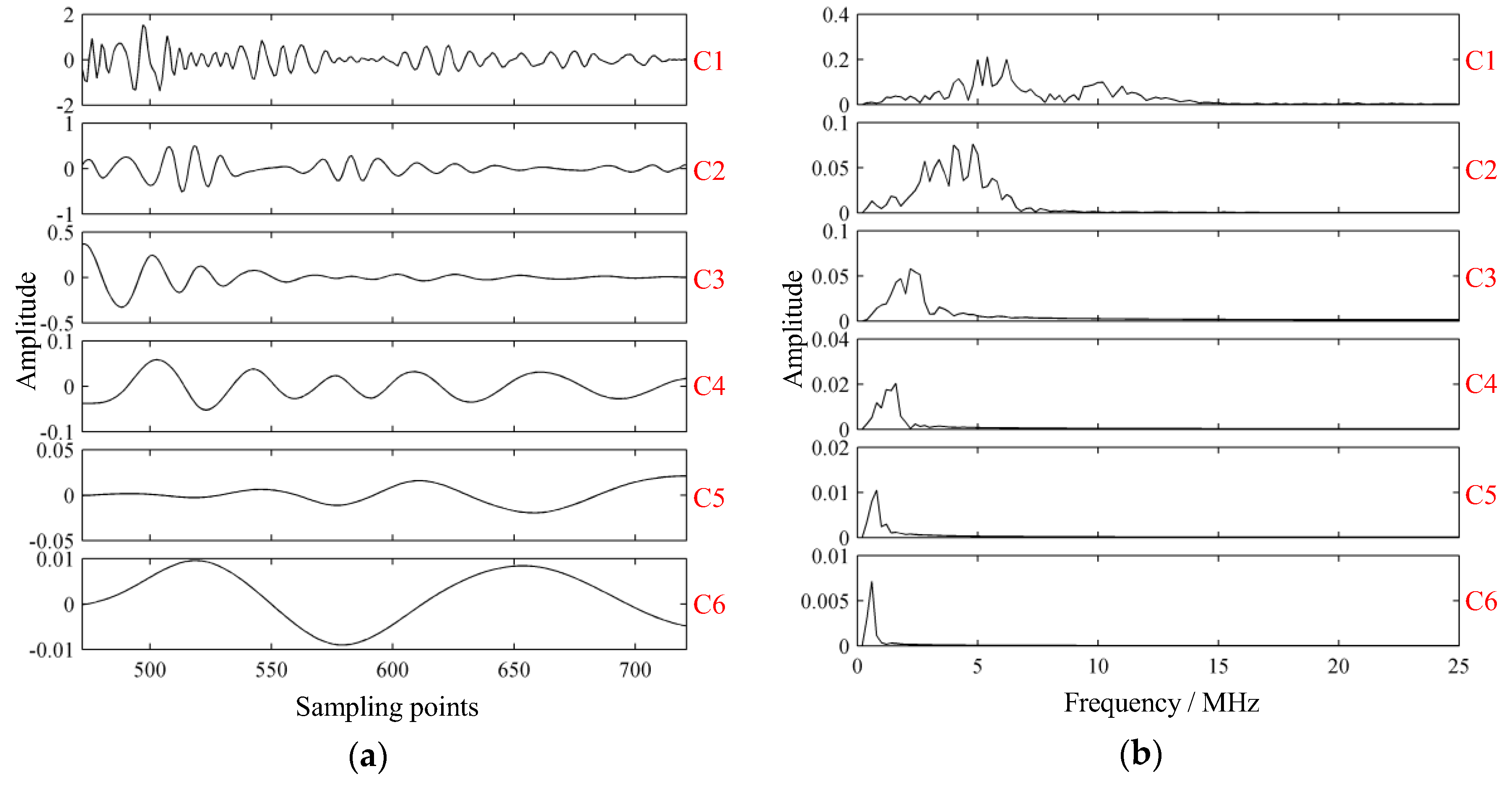
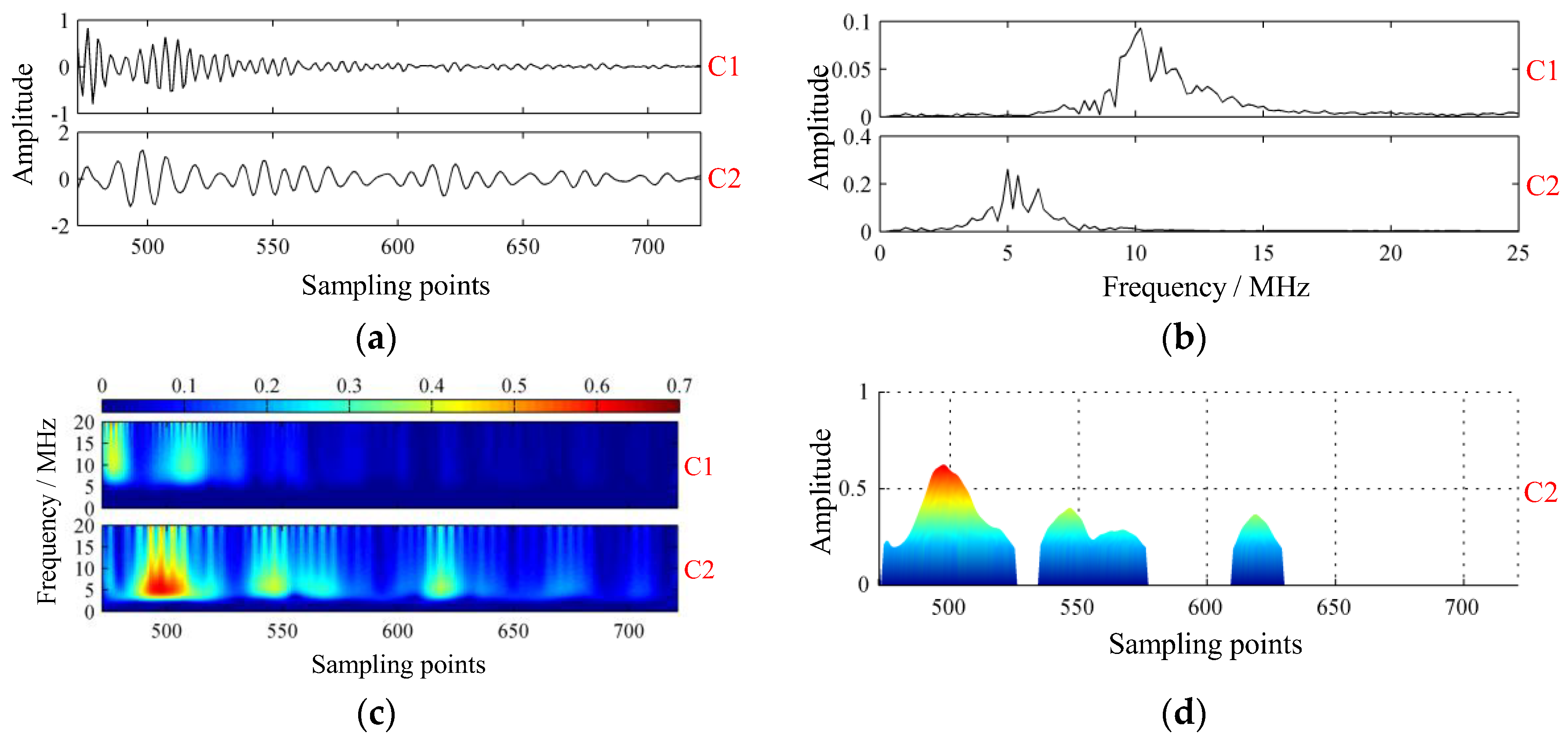
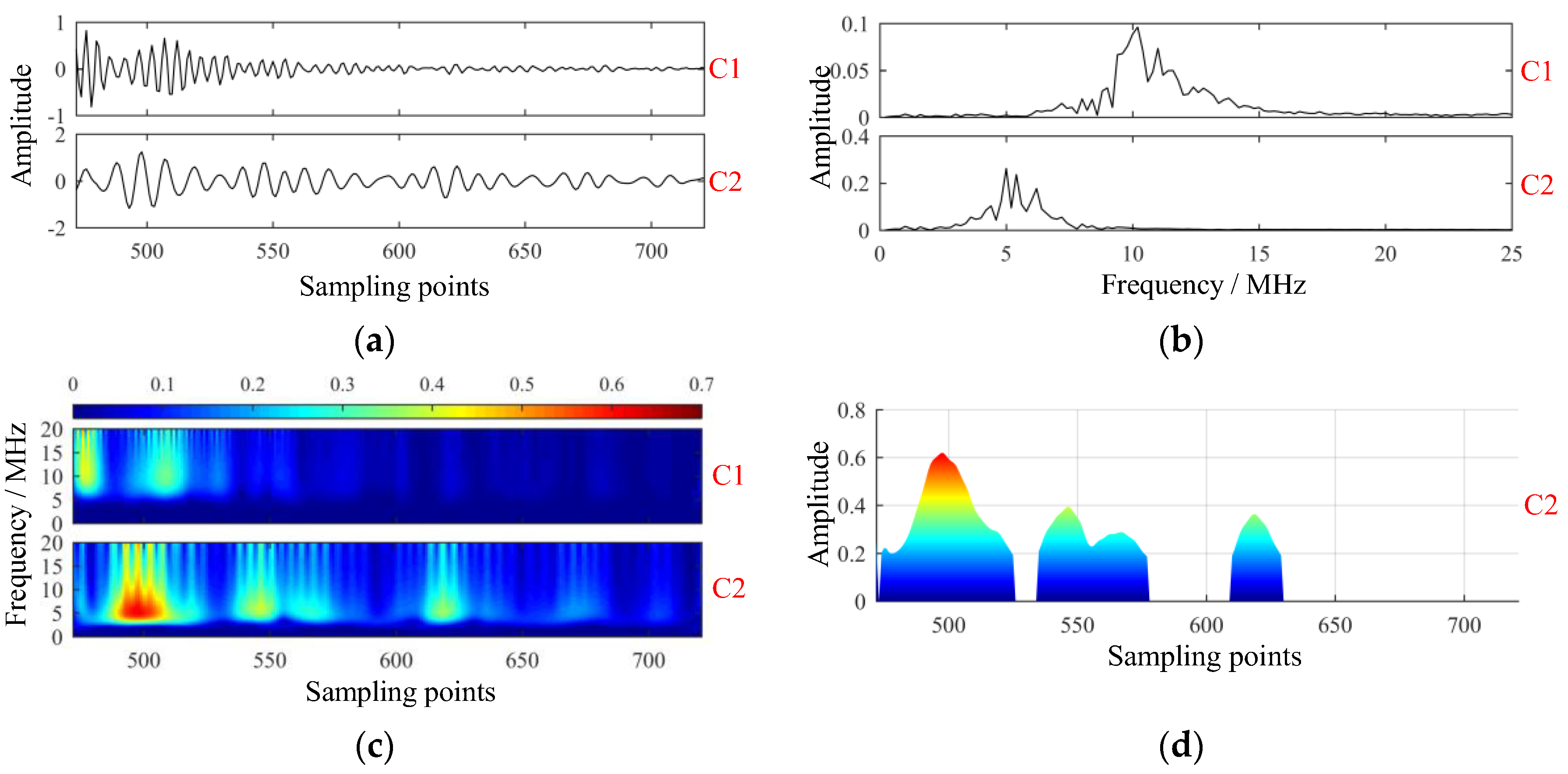
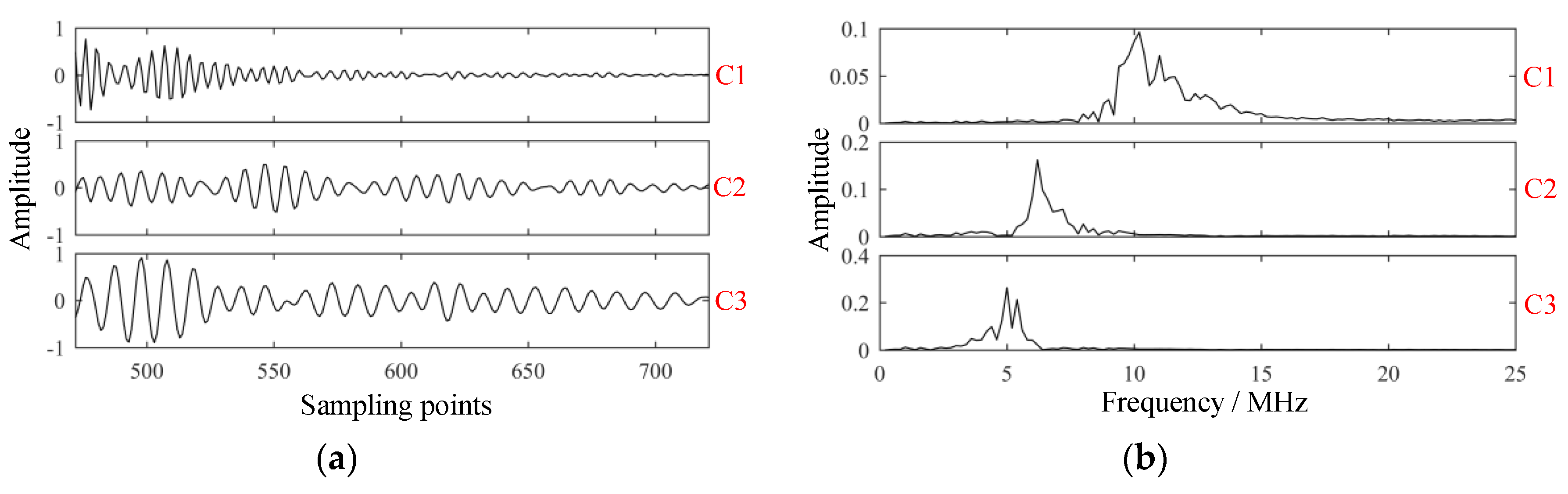
4.2. Simulation of Typical Cases
4.3. Model Simplification
5. Experimental Study
5.1. Experimental System
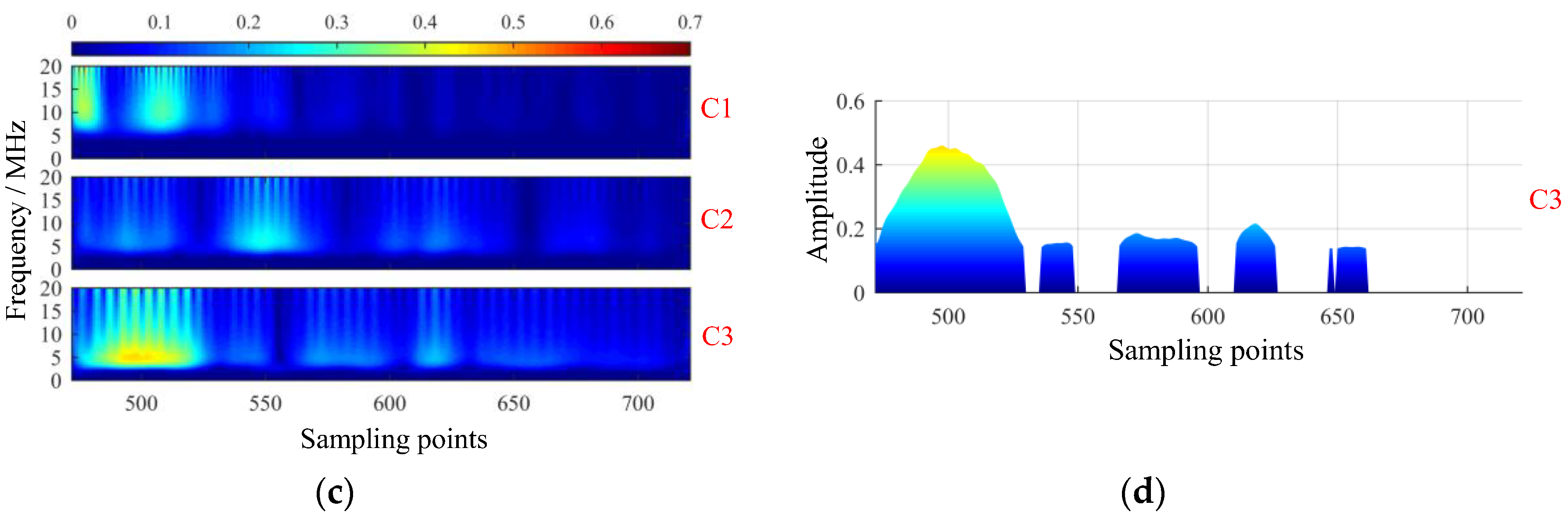
5.2. Analysis of Backscattered Signals
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Martin, B.G. Ultrasonic wave-propagation in fiber-reinforced solids containing voids. J. Appl. Phys. 1977, 48, 3368–3373. [Google Scholar] [CrossRef]
- Nair, S.M.; Hsu, D.K.; Rose, J.H. Porosity estimation using the frequency dependence of the ultrasonic attenuation. J. Nondestruct. Eval. 1989, 8, 13–26. [Google Scholar] [CrossRef]
- Jeong, H.; Hsu, D.K. Experimental analysis of porosity-induced ultrasonic attenuation and velocity change in carbon composites. Ultrasonics 1995, 33, 195–203. [Google Scholar] [CrossRef]
- Lin, L.; Luo, M.; Guo, G.P.; Li, X.M. Ultrasonic determination of carbon fiber composite porosity using acoustic impedance. Acta Mater. Compos. Sin. 2009, 26, 105–110. [Google Scholar] [CrossRef]
- Grolemund, D.; Tsai, C.S. Statistical moments of backscattered ultrasound in porous fiber reinforced composites. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1998, 45, 295–304. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.B.; Hsu, D.K.; Barnard, D.J. Estimation of porosity content of composite materials by applying discrete wavelet transform to ultrasonic backscattered signal. NDT Int. 2013, 56, 10–16. [Google Scholar] [CrossRef]
- Karabutov, A.A.; Podymova, N.B. Nondestructive porosity assessment of CFRP composites with spectral analysis of backscattered laser-induced ultrasonic pulses. J. Nondestruct. Eval. 2013, 32, 315–324. [Google Scholar] [CrossRef]
- Chen, Y.C.; Yang, C.L.; Zhou, X.J.; Li, Z.; Zheng, H.F. CFRP voids 3D identification and location method based on the process of backscattered signal. J. Wuhan Univ. Technol. Mater. Sci. Ed. 2016, 31, 172–177. [Google Scholar] [CrossRef]
- Yu, Y.L.; Ye, J.R.; Wang, Y.; Zhang, B.M.; Qi, G.C. A mesoscale ultrasonic attenuation finite element model of composites with random-distributed voids. Compos. Sci. Technol. 2013, 89, 44–51. [Google Scholar] [CrossRef]
- Biwa, S.; Watanabe, Y.; Motogi, S.; Ohno, N. Analysis of ultrasonic attenuation in particle-reinforced plastics by a differential scheme. Ultrasonics 2004, 43, 5–12. [Google Scholar] [CrossRef] [PubMed]
- Reverdy, F.; Mahaut, S.; Dominguez, N.; Dubois, P. Simulation of ultrasonic inspection of curved composites using a hybrid semi-analytical/numerical code. In Proceedings of the 41st Annual Review of Progress in Quantitative Nondestructive Evalution, Boise, ID, USA, 20–25 July 2014; Chimenti, D.E., Bond, L.J., Eds.; Amer Inst Physics: Warren, NJ, USA, 2015; pp. 1047–1055. [Google Scholar] [CrossRef]
- Tayong, R.B.; Smith, R.A.; Pinfield, V.J. Acoustic characterization of void distributions across carbon-fiber composite layers. In Proceedings of the 42nd Annual Review of Progress in Quantitative Nondestructive Evalution: Incorporating the 6th European-American Workshop on Reliability of NDE, Minneapolis, MN, USA, 26–31 July 2015; Chimenti, D.E., Bond, L.J., Eds.; Amer Inst Physics: Warren, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Scott, W.R.; Gordon, P.F. Ultrasonic spectrum analysis for nondestructive testing of layered composite materials. J. Acoust. Soc. Am. 1977, 62, 108–116. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Sig. Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Stockwell, R.G.; Mansinha, L.; Lowe, R.P. Localization of the complex spectrum: The S transform. IEEE Trans. Sig. Process. 1996, 44, 998–1001. [Google Scholar] [CrossRef]
- Assous, S.; Boashash, B. Evaluation of the modified S-transform for time-frequency synchrony analysis and source localization. EURASIP 2012, 49, 1–18. [Google Scholar] [CrossRef]
- Hagglund, F.; Martinsson, J.; Carlson, J.E. Model-based estimation of thin multi-layered media using ultrasonic measurements. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 1689–1702. [Google Scholar] [CrossRef] [PubMed]
- Ying, C.F.; Truell, R. Scattering of a plane longitudinal wave by a spherical obstacle in an isotropically elastic solid. J. Appl. Phys. 1956, 27, 1086–1097. [Google Scholar] [CrossRef]
- Demirli, R.; Saniie, J. Asymmetric Gaussian chirplet model and parameter estimation for generalized echo representation. J. Frankl. Inst. Eng. Appl. Math. 2014, 351, 907–921. [Google Scholar] [CrossRef]
- Gustafsson, M.G.; Stepinski, T. Studies of split spectrum processing, optimal detection, and maximum likelihood amplitude estimation using a simple clutter model. Ultrasonics 1997, 35, 31–52. [Google Scholar] [CrossRef]
- Rilling, G.; Flandrin, P. One or two frequencies? The empirical mode decomposition answers. IEEE Trans. Signal Process. 2008, 56, 85–95. [Google Scholar] [CrossRef]
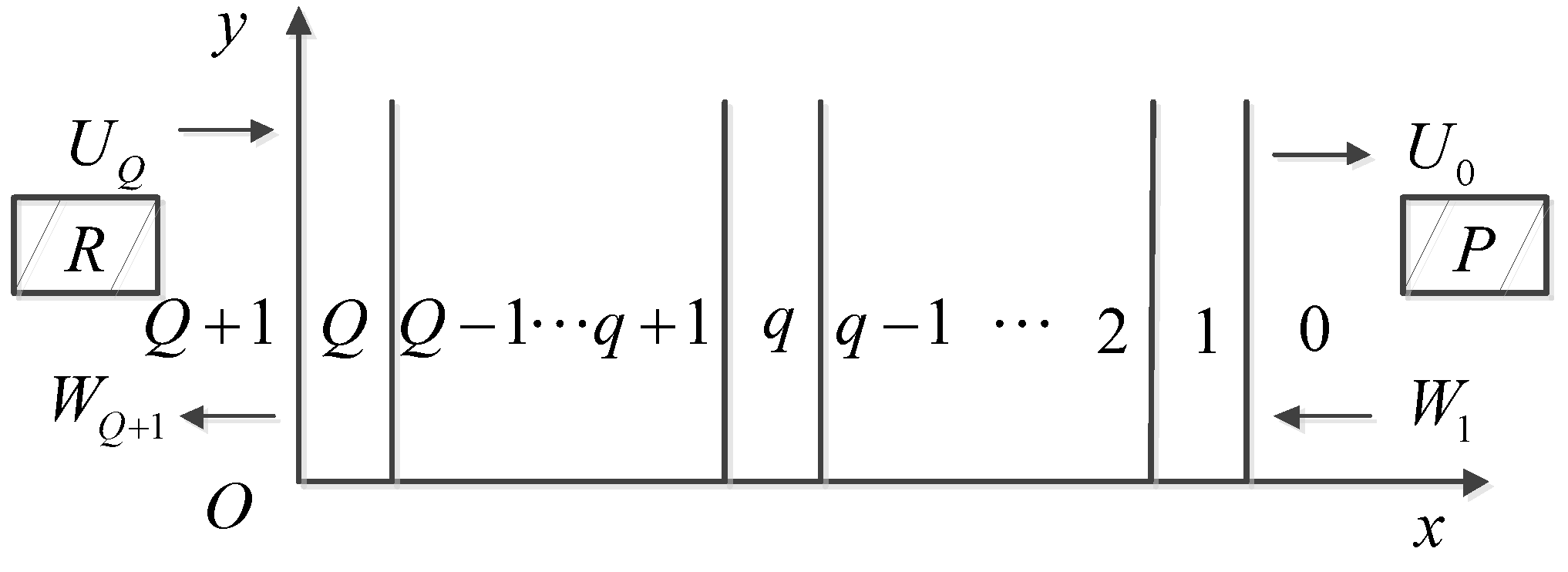








| 1690 | 3077 | 1770 | 0.150 | 1270 | 2903 | 0.005 | 48 | 5% |
| a (μm) | Nv | dmin (cm) | nv1 | nv2 | λv | nr | λr |
|---|---|---|---|---|---|---|---|
| 10 | 3000 | 1.0 | 29 | 31 | 5 | 30 | 8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, W.; Zhou, X.; Zeng, X.; Yang, C. Ultrasonic Inspection of Localized Defects in Low-Porosity CFRP. Sensors 2019, 19, 1654. https://doi.org/10.3390/s19071654
Feng W, Zhou X, Zeng X, Yang C. Ultrasonic Inspection of Localized Defects in Low-Porosity CFRP. Sensors. 2019; 19(7):1654. https://doi.org/10.3390/s19071654
Chicago/Turabian StyleFeng, Wei, Xiaojun Zhou, Xiang Zeng, and Chenlong Yang. 2019. "Ultrasonic Inspection of Localized Defects in Low-Porosity CFRP" Sensors 19, no. 7: 1654. https://doi.org/10.3390/s19071654




