Modelling, Analysis, and Simulation of the Micro-Doppler Effect in Wideband Indoor Channels with Confirmation Through Pendulum Experiments
Abstract
:1. Introduction
2. The 3D Geometrical Model
3. The Channel Transfer Function
4. Spectrogram Analysis
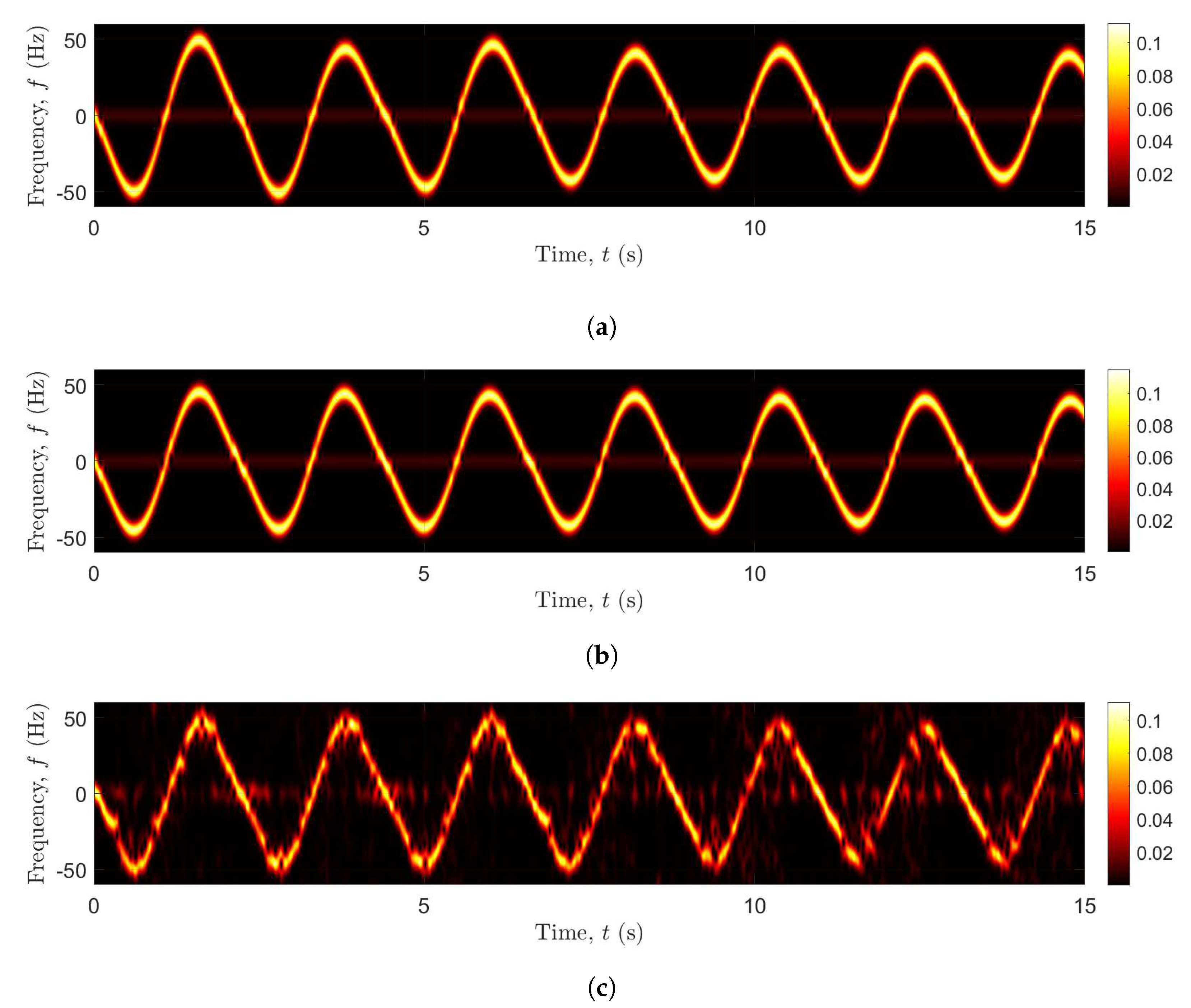
5. Measurements and Numerical Results
5.1. Measurement Scenario
5.2. Motion Capturing Using IMU
5.3. Capturing CSI Data
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Jian, M.; Lu, Z.; Chen, V.C. Drone detection and tracking based on phase-interferometric Doppler radar. In Proceedings of the IEEE Radar Conference (RadarConf18), Oklahoma City, OK, USA, 23–27 April 2018; pp. 1146–1149. [Google Scholar] [CrossRef]
- Amin, M.G.; Zeng, Z.; Shan, T. Hand Gesture Recognition based on Radar Micro-Doppler Signature Envelopes. In Proceedings of the IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Seifert, A.; Zoubir, A.M.; Amin, M.G. Detection of gait asymmetry using indoor Doppler radar. In Proceedings of the IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Adib, F.; Kabelac, Z.; Katabi, D.; Miller, R.C. 3D tracking via body radio reflections. In Proceedings of the 11th USENIX Conference on Networked Systems Design and Implementation NSDI’14, Seattle, WA, USA, 2–4 April 2014; USENIX Association: Berkeley, CA, USA, 2014; pp. 317–329. [Google Scholar]
- Pham, V.H.; Taieb, M.H.; Chouinard, J.Y.; Roy, S.; Huynh, H.T. On the double Doppler effect generated by scatterer motion. REV J. Electron. Commun. 2011, 1, 30–37. [Google Scholar] [CrossRef] [Green Version]
- Abdelgawwad, A.; Pätzold, M. On the influence of walking people on the Doppler spectral characteristics of indoor channels. In Proceedings of the 28th IEEE Int. Symp. on Personal, Indoor and Mobile Radio Communications, PIMRC 2017, Montreal, QC, Canada, 8–13 October 2017. [Google Scholar]
- Abdelgawwad, A.; Paetzold, M. A 3D non-Stationary cluster channel model for human activity recognition. In Proceedings of the IEEE 89th Vehicular Technology Conference (VTC2019-Spring), Kuala Lumpur, Malaysia, 28 April–1 May 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Bian, J.; Wang, C.; Zhang, M.; Ge, X.; Gao, X. A 3-D Non-stationary wideband MIMO channel model allowing for velocity variations of the mobile station. In Proceedings of the IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Gurbuz, S.Z.; Clemente, C.; Balleri, A.; Soraghan, J.J. Micro-Doppler-based in-home aided and unaided walking recognition with multiple radar and sonar systems. IET Radar Sonar Navig. 2017, 11, 107–115. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Wang, P.; Cao, X.; Chen, V.C. Interferometric angular velocity measurement of rotating blades: Theoretical analysis, modeling and simulation study. IET Radar Sonar Navig. 2019, 13, 438–444. [Google Scholar] [CrossRef]
- Ritchie, M.; Jones, A.M. Micro-Doppler gesture recognition using Doppler, time and range based features. In Proceedings of the IEEE Radar Conference (RadarConf), Boston, Ma, USA, 22–26 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Erol, B.; Amin, M.G. Radar data cube processing for human activity recognition using multi subspace learning. IEEE Trans. Aerosp. Electron. Syst. 2019. [Google Scholar] [CrossRef]
- Seifert, A.; Amin, M.G.; Zoubir, A.M. Toward unobtrusive in-home gait analysis based on radar micro-Doppler signatures. IEEE Trans. Biomed. Eng. 2019, 66, 2629–2640. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fioranelli, F.; Ritchie, M.; Gürbüz, S.Z.; Griffiths, H. Feature diversity for optimized human micro-Doppler classification using multistatic radar. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 640–654. [Google Scholar] [CrossRef]
- Wu, M.; Dai, X.; Zhang, Y.D.; Davidson, B.; Amin, M.G.; Zhang, J. Fall detection based on sequential modeling of radar signal time-frequency features. In Proceedings of the IEEE International Conference on Healthcare Informatics, Philadelphia, PA, USA, 9–11 September 2013; pp. 169–174. [Google Scholar] [CrossRef]
- Amin, M.G.; Zhang, Y.D.; Ahmad, F.; Ho, K.C.D. Radar signal processing for elderly fall detection: The future for in-home monitoring. IEEE Signal Process. Mag. 2016, 33, 71–80. [Google Scholar] [CrossRef]
- Jokanović, B.; Amin, M. Fall detection using deep learning in range-Doppler radars. IEEE Trans. Aeros. Electron. Syst. 2018, 54, 180–189. [Google Scholar] [CrossRef]
- Halperin, D.; Hu, W.; Sheth, A.; Wetherall, D. Tool Release: Gathering 802.11n traces with channel state information. ACM SIGCOMM CCR 2011, 41, 53. [Google Scholar] [CrossRef]
- IEEE Standard for Information technology—Local and metropolitan area networks—Specific requirements—Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications Amendment 5: Enhancements for Higher Throughput. In IEEE Std 802.11n-2009 (Amendment to IEEE Std 802.11-2007 as Amended by IEEE Std 802.11k-2008, IEEE Std 802.11r-2008, IEEE Std 802.11y-2008, and IEEE Std 802.11w-2009); IEEE: Piscataway, NJ, USA, 2009; pp. 1–565. [CrossRef]
- Wang, Z.; Guo, B.; Yu, Z.; Zhou, X. Wi-Fi CSI-based behavior recognition: From signals and actions to activities. IEEE Commun. Mag. 2018, 56, 109–115. [Google Scholar] [CrossRef]
- Wang, X.; Yang, C.; Mao, S. PhaseBeat: Exploiting CSI phase data for vital sign monitoring with commodity WiFi devices. In Proceedings of the IEEE 37th International Conference on Distributed Computing Systems (ICDCS), Atlanta, GA, USA, 5–8 June 2017; pp. 1230–1239. [Google Scholar] [CrossRef]
- Xie, Y.; Li, Z.; Li, M. Precise power delay profiling with commodity WiFi. In Proceedings of the 21st Annual International Conference on Mobile Computing and Networking, MobiCom ’15, Beijing, China, 20–25 September 2015; ACM: New York, NY, USA, 2015; pp. 53–64. [Google Scholar] [CrossRef]
- Vasisht, D.; Kumar, S.; Katabi, D. Decimeter-level localization with a single WiFi access point. In Proceedings of the 13th Usenix Conference on Networked Systems Design and Implementation, NSDI’16, Santa Clara, CA, USA, 16–18 March 2016; USENIX Association: Berkeley, CA, USA, 2016; pp. 165–178. [Google Scholar]
- Gong, L.; Yang, W.; Man, D.; Dong, G.; Yu, M.; Lv, J. WiFi-based real-time calibration-free passive human motion detection. Sensors 2015, 15, 32213–32229. [Google Scholar] [CrossRef] [Green Version]
- Mahfoudi, M.N.; Turletti, T.; Parmentelat, T.; Ferrero, F.; Lizzi, L.; Staraj, R.; Dabbous, W. ORION: Orientation estimation using commodity Wi-Fi. In Proceedings of the IEEE International Conference on Communications Workshops (ICC Workshops), Paris, France, 21–25 May 2017; pp. 1233–1238. [Google Scholar] [CrossRef] [Green Version]
- Kotaru, M.; Joshi, K.; Bharadia, D.; Katti, S. SpotFi: Decimeter level localization using WiFi. SIGCOMM Comput. Commun. Rev. 2015, 45, 269–282. [Google Scholar] [CrossRef]
- Qian, K.; Wu, C.; Yang, Z.; Zhou, Z.; Wang, X.; Liu, Y. Tuning by turning: Enabling phased array signal processing for WiFi with inertial sensors. In Proceedings of the IEEE INFOCOM 2016—The 35th Annual IEEE International Conference on Computer Communications, San Francisco, CA, USA, 10–15 April 2015–2016; pp. 1–9. [Google Scholar] [CrossRef]
- Zhuo, Y.; Zhu, H.; Xue, H. Identifying a new non-ninear CSI phase measurement error with commodity WiFi devices. In Proceedings of the 2016 IEEE 22nd International Conference on Parallel and Distributed Systems (ICPADS), Wuhan, China, 13–16 December 2016; pp. 72–79. [Google Scholar] [CrossRef]
- Wang, W.; Liu, A.X.; Shahzad, M. Gait recognition using Wifi signals. In Proceedings of the 2016 ACM International Joint Conference on Pervasive and Ubiquitous Computing, UbiComp ’16, Heidelberg, Germany, 12–16 September 2016; ACM: New York, NY, USA, 2016; pp. 363–373. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Chu, Z.; Yang, P.; Xiang, C.; Zheng, X.; Huang, W. TW-See: Human activity recognition through the wall with commodity Wi-Fi devices. IEEE Trans. Veh/ Technol. 2019, 68, 306–319. [Google Scholar] [CrossRef]
- Du, C.; Yuan, X.; Lou, W.; Hou, Y.T. Context-free fine-grained motion sensing using WiFi. In Proceedings of the 15th Annual IEEE International Conference on Sensing, Communication and Networking (SECON), Hong Kong, 11–13 June 2018; pp. 1–9. [Google Scholar] [CrossRef]
- Chen, J.; Li, F.; Chen, H.; Yang, S.; Wang, Y. Dynamic gesture recognition using wireless signals with less disturbance. Pers. Ubiquitous Comput. 2019, 23, 17–27. [Google Scholar] [CrossRef]
- Sen, S.; Radunovic, B.; Choudhury, R.R.; Minka, T. You are facing the mona lisa: Spot localization using PHY layer information. In Proceedings of the 10th International Conference on Mobile Systems, Applications, and Services, MobiSys ’12, Ambleside, UK, 25–29 June 2012; ACM: New York, NY, USA, 2012; pp. 183–196. [Google Scholar] [CrossRef]
- Qian, K.; Wu, C.; Yang, Z.; Liu, Y.; Zhou, Z. PADS: Passive detection of moving targets with dynamic speed using PHY layer information. In Proceedings of the 20th IEEE International Conference on Parallel and Distributed Systems (ICPADS), Hsinchu, Taiwan, 16–19 December 2014; pp. 1–8. [Google Scholar] [CrossRef]
- Keerativoranan, N.; Haniz, A.; Saito, K.; Takada, J.I. Mitigation of CSI temporal phase rotation with B2B calibration method for fine-grained motion detection analysis on commodity Wi-Fi devices. Sensors 2018, 18, 3795. [Google Scholar] [CrossRef]
- Abdullah, R.S.A.R.; Alnaeb, A.; Salah, A.A.; Rashid, N.E.A.; Sali, A.; Pasya, I. Micro-Doppler estimation and analysis of slow moving objects in forward scattering radar system. Remote Sens. 2017, 9, 699. [Google Scholar] [CrossRef] [Green Version]
- Chen, V. The Micro-Doppler Effect in Radar, 2nd ed.; Artech House Radar Library; Artech House: Norwood, MA, USA, 2019. [Google Scholar]
- Dauger, D.E. Simulation and study of Fresnel diffraction for arbitrary two-dimensional apertures. Comput. Phys. 1996, 10, 591–604. [Google Scholar] [CrossRef]
- He, R.; Zhong, Z.; Ai, B.; Ding, J.; Guan, K. Analysis of the relation between Fresnel zone and path loss exponent based on two-ray Model. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 208–211. [Google Scholar] [CrossRef]
- Goldsmith, A. Wireless Communications; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef] [Green Version]
- Rappaport, T. Wireless Communications: Principles and Practice, 2nd ed.; Prentice Hall PTR: Upper Saddle River, PJ, USA, 2001. [Google Scholar]
- Zhang, F.; Niu, K.; Xiong, J.; Jin, B.; Gu, T.; Jiang, Y.; Zhang, D. Towards a diffraction-based sensing approach on human activity recognition. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2019, 3. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, D.; Xiong, J.; Wang, H.; Niu, K.; Jin, B.; Wang, Y. From Fresnel diffraction model to fine-grained human respiration sensing with commodity Wi-Fi devices. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2018, 2, 1–23. [Google Scholar] [CrossRef]
- Xin, T.; Guo, B.; Wang, Z.; Wang, P.; Lam, J.C.K.; Li, V.O.K.; Yu, Z. FreeSense: A robust approach for indoor human detection using Wi-Fi signals. IMWUT 2018, 2, 143:1–143:23. [Google Scholar] [CrossRef]
- Yun, X.; Bachmann, E.R.; Moore, H.; Calusdian, J. Self-contained position tracking of human movement using small inertial/magnetic sensor modules. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 2526–2533. [Google Scholar] [CrossRef]
- MATLAB Code for 3D Tracking with IMU. Available online: https://github.com/xioTechnologies/Gait-Tracking-With-x-IMU (accessed on 13 February 2020).
- Pätzold, M.; Gutierrez, C.A. Modelling of non-WSSUS channels with time-variant Doppler and delay characteristics. In Proceedings of the IEEE Seventh International Conference on Communications and Electronics (ICCE), Hue, Vietnam, 18–20 July 2018; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Abdelgawwad, A.; Pätzold, M. A framework for activity monitoring and fall detection based on the characteristics of indoor channels. In Proceedings of the IEEE 87th Vehicular Technology Conference (VTC Spring), Porto, Portugal, 3–6 June 2018. [Google Scholar] [CrossRef] [Green Version]
- Pätzold, M.; Gutiérrez, C.A.; Youssef, N. On the consistency of non-stationary multipath fading channels with respect to the average Doppler shift and the Doppler spread. In Proceedings of the IEEE Wireless Communications and Networking Conference, WCNC, San Francisco, CA, USA, 19–22 March 2017. [Google Scholar] [CrossRef] [Green Version]
- Boashash, B. Time-Frequency Signal Analysis and Processing—A Comprehensive Reference, 2nd ed.; Elsevier: Amsterdam, The Netherlands; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Sensors for Motion Capture, Biomechanics, Industrial Control, Robotics, Facility Management, Cold Storage, Research, and Product Development. Available online: https://mbientlab.com/ (accessed on 13 February 2020).






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelgawwad, A.; Borhani, A.; Pätzold, M. Modelling, Analysis, and Simulation of the Micro-Doppler Effect in Wideband Indoor Channels with Confirmation Through Pendulum Experiments. Sensors 2020, 20, 1049. https://doi.org/10.3390/s20041049
Abdelgawwad A, Borhani A, Pätzold M. Modelling, Analysis, and Simulation of the Micro-Doppler Effect in Wideband Indoor Channels with Confirmation Through Pendulum Experiments. Sensors. 2020; 20(4):1049. https://doi.org/10.3390/s20041049
Chicago/Turabian StyleAbdelgawwad, Ahmed, Alireza Borhani, and Matthias Pätzold. 2020. "Modelling, Analysis, and Simulation of the Micro-Doppler Effect in Wideband Indoor Channels with Confirmation Through Pendulum Experiments" Sensors 20, no. 4: 1049. https://doi.org/10.3390/s20041049




