High-Refractive-Index Materials for Giant Enhancement of the Transverse Magneto-Optical Kerr Effect
Abstract
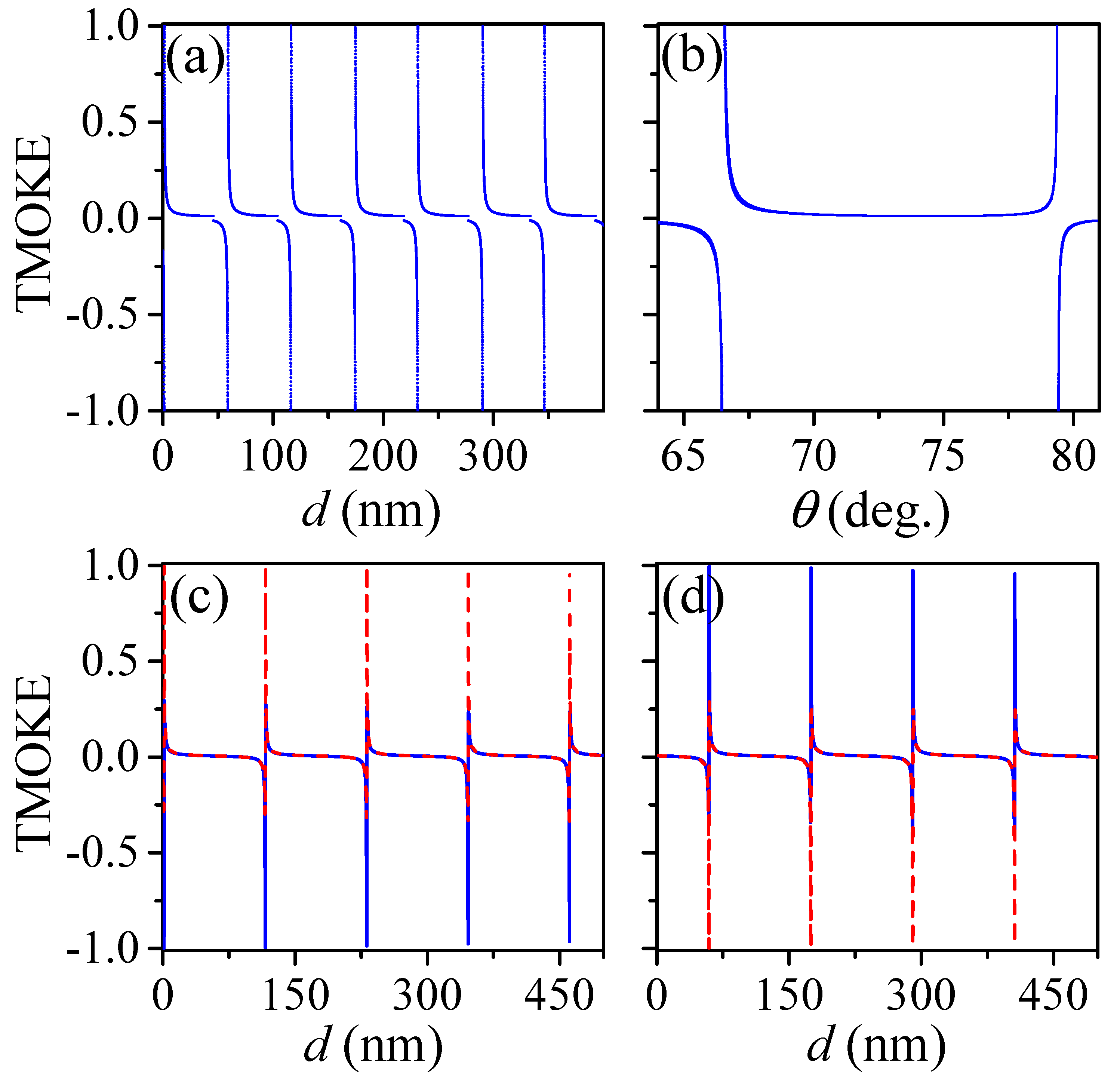
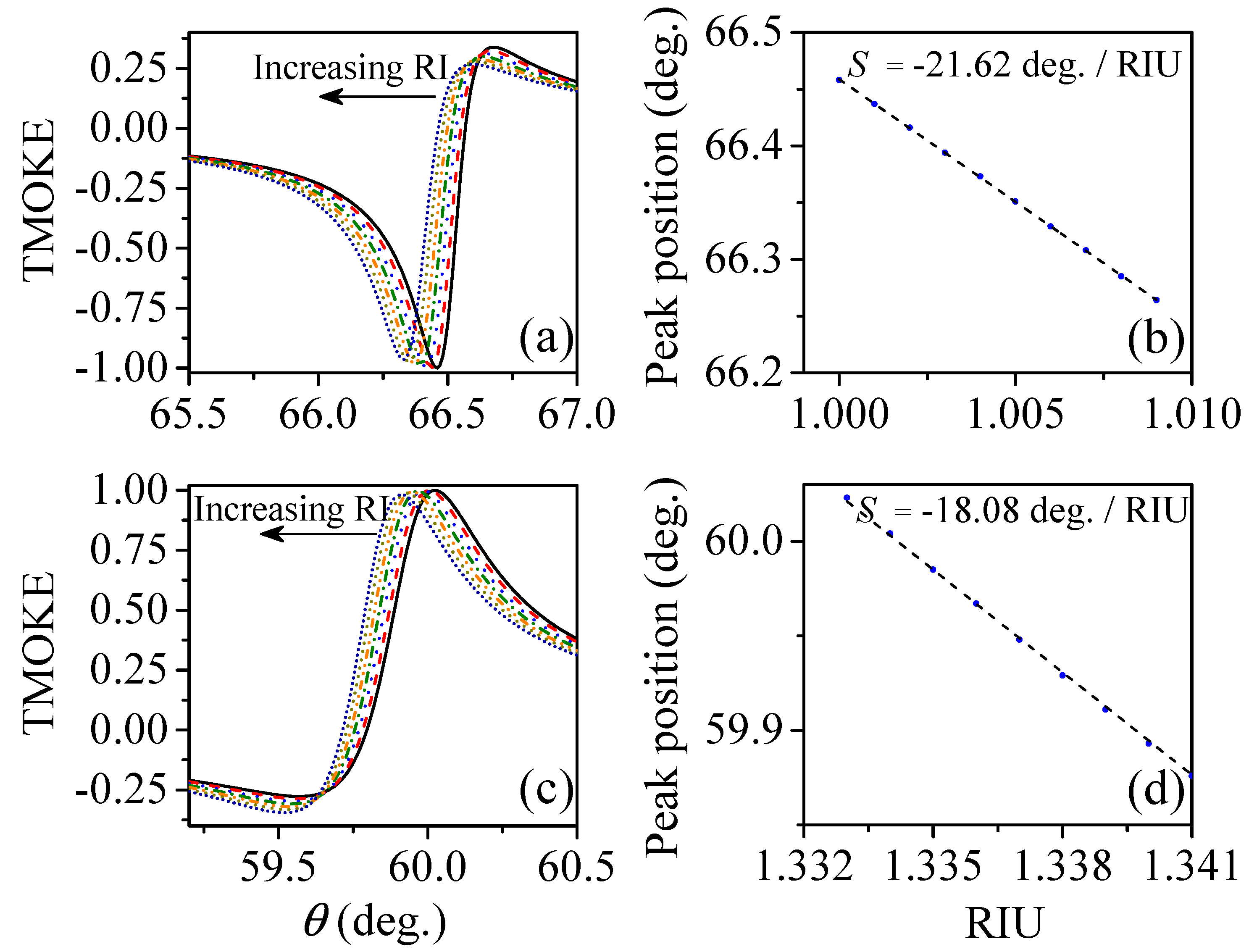
:1. Introduction
2. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Belotelov, V.I.; Bykov, D.A.; Doskolovich, L.L.; Kalish, A.N.; Zvezdin, A.K. Extraordinary transmission and giant magneto-optical transverse Kerr effect in plasmonic nanostructured films. J. Opt. Soc. Am. B 2009, 26, 1594. [Google Scholar] [CrossRef]
- Belotelov, V.I.; Bykov, D.A.; Doskolovich, L.L.; Kalish, A.N.; Zvezdin, A.K. Giant transversal Kerr effect in magneto-plasmonic heterostructures: The scattering-matrix method. J. Exp. Theor. Phys. 2010, 110, 816–824. [Google Scholar] [CrossRef]
- Grunin, A.A.; Zhdanov, A.G.; Ezhov, A.A.; Ganshina, E.A.; Fedyanin, A.A. Surface-plasmon-induced enhancement of magneto-optical Kerr effect in all-nickel subwavelength nanogratings. Appl. Phys. Lett. 2010, 97, 261908. [Google Scholar] [CrossRef] [Green Version]
- Belotelov, V.I.; Akimov, I.A.; Pohl, M.; Kotov, V.A.; Kasture, S.; Vengurlekar, A.S.; Gopal, A.V.; Yakovlev, D.R.; Zvezdin, A.K.; Bayer, M. Enhanced magneto-optical effects in magnetoplasmonic crystals. Nat. Nanotech. 2011, 6, 370–376. [Google Scholar] [CrossRef] [PubMed]
- Pohl, M.; Kreilkamp, L.E.; Belotelov, V.I.; Akimov, I.A.; Kalish, A.N.; Khokhlov, N.E.; Yallapragada, V.J.; Gopal, A.V.; Nur-E-Alam, M.; Vasiliev, M.; et al. Tuning of the transverse magneto-optical Kerr effect in magneto-plasmonic crystals. New J. Phys. 2013, 15, 075024. [Google Scholar] [CrossRef] [Green Version]
- Kreilkamp, L.E.; Belotelov, V.I.; Chin, J.Y.; Neutzner, S.; Dregely, D.; Wehlus, T.; Akimov, I.A.; Bayer, M.; Stritzker, B.; Giessen, H. Waveguide-Plasmon Polaritons Enhance Transverse Magneto-Optical Kerr Effect. Phys. Rev. X 2013, 3, 041019. [Google Scholar] [CrossRef] [Green Version]
- Borovkova, O.V.; Hashim, H.; Kozhaev, M.A.; Dagesyan, S.A.; Chakravarty, A.; Levy, M.; Belotelov, V.I. TMOKE as efficient tool for the magneto-optic analysis of ultra-thin magnetic films. Appl. Phys. Lett. 2018, 112, 063101. [Google Scholar] [CrossRef] [Green Version]
- Davoyan, A.R.; Mahmoud, A.M.; Engheta, N. Optical isolation with epsilon-near-zero metamaterials. Opt. Exp. 2013, 21, 3279–3286. [Google Scholar] [CrossRef]
- Moccia, M.; Castaldi, G.; Galdi, V.; Alù, A.; Engheta, N. Enhanced Faraday rotation via resonant tunnelling in tri-layers containing magneto-optical metals. J. Phys. D Appl. Phys. 2014, 47, 025002. [Google Scholar] [CrossRef] [Green Version]
- Moccia, M.; Castaldi, G.; Galdi, V.; Alù, A.; Engheta, N. Optical isolation via unidirectional resonant photon tunneling. J. Appl. Phys. 2014, 115, 043107. [Google Scholar] [CrossRef] [Green Version]
- Kaihara, T.; Ando, T.; Shimizu, H.; Zayets, V.; Saito, H.; Ando, K.; Yuasa, S. Enhancement of magneto-optical Kerr effect by surface plasmons in trilayer structure consisting of double-layer dielectrics and ferromagnetic metal. Opt. Exp. 2015, 23, 11537. [Google Scholar] [CrossRef]
- Abdi-Ghaleh, R.; Suldozi, R. Magneto-optical characteristics of layered Epsilon-Near-Zero metamaterials. Supperlat. Microstruct. 2016, 97, 242–249. [Google Scholar] [CrossRef]
- Luo, X.; Zhou, M.; Liu, J.; Qiu, T.; Yu, Z. Magneto-optical metamaterials with extraordinarily strong magneto-optical effect. Appl. Phys. Lett. 2016, 108, 131104. [Google Scholar] [CrossRef]
- Chizhik, A.; Zhukov, A.; Blanco, J.M.; Gonzalez, J. Magneto-optical investigation of magnetization reversal in nearly zero magnetostrictive Co-rich wire and microwire. J. Magn. Magn. Mater. 2002, 249, 27–33. [Google Scholar] [CrossRef]
- Rzhevsky, A.A.; Krichevtsov, B.B.; Bürgler, D.E.; Schneider, C.M. Interfacial magnetization in exchange-coupled Fe/Cr/Fe structures investigated by second harmonic generation. Phys. Rev. B 2007, 75, 144416. [Google Scholar] [CrossRef] [Green Version]
- Kämpf, K.; Kübler, S.; Herberg, F.W.; Ehresmann, A. Magneto-optic surface plasmon resonance optimum layers: Simulations for biological relevant refractive index changes. J. Appl. Phys. 2012, 112, 034505. [Google Scholar] [CrossRef] [Green Version]
- Shoji, Y.; Shirato, Y.; Mizumoto, T. Silicon Mach-Zehnder interferometer optical isolator having 8 nm bandwidth for over 20 dB isolation. Jpn. J. Appl. Phys. 2014, 53, 022202. [Google Scholar] [CrossRef]
- Caballero, B.; García-Martín, A.; Cuevas, J.C. Hybrid Magnetoplasmonic Crystals Boost the Performance of Nanohole Arrays as Plasmonic Sensors. ACS Photonics 2016, 3, 203–208. [Google Scholar] [CrossRef]
- Kimel, A.V.; Kirilyuk, A.; Usachev, P.A.; Pisarev, R.V.; Balbashov, A.M.; Rasing, T. Ultrafast non-thermal control of magnetization by instantaneous photomagnetic pulses. Nature 2005, 435, 655–657. [Google Scholar] [CrossRef]
- Vahaplar, K.; Kalashnikova, A.M.; Kimel, A.V.; Hinzke, D.; Nowak, U.; Chantrell, R.; Tsukamoto, A.; Itoh, A.; Kirilyuk, A.; Rasing, T. Ultrafast Path for Optical Magnetization Reversal via a Strongly Nonequilibrium State. Phys. Rev. Lett. 2009, 103, 117201. [Google Scholar] [CrossRef] [Green Version]
- Kirilyuk, A.; Kimel, A.V.; Rasing, T. Ultrafast optical manipulation of magnetic order. Rev. Mod. Phys. 2010, 82, 2731. [Google Scholar] [CrossRef]
- Višňovský, Š.; Lišková-Jakubisobá, E.; Harward, I.; Celinski, Z. Transverse magnetooptic effect in multilayers applied to mapping of microwave currents. Opt. Mater. Exp. 2017, 7, 2368. [Google Scholar] [CrossRef]
- Khramova, A.E.; Ignatyeva, D.O.; Kozhaev, M.A.; Dagesyan, S.A.; Berzhansky, V.N.; Shaposhnikov, A.N.; Tomilin, S.V.; Belotelov, V.I. Resonances of the magneto-optical intensity effect mediated by interaction of different modes in a hybrid magnetoplasmonic heterostructure with gold nanoparticles. Opt. Exp. 2019, 27, 33170–33179. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zvezdin, A.K.; Kotov, V.A. Modern Magnetooptics and Magnetooptical Materials, 1st ed.; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Girón-Sedas, J.A.; Gómez, F.R.; Albella, P.; Mejía-Salazar, J.R.; Oliveira, O.N., Jr. Giant enhancement of the transverse magneto-optical Kerr effect through the coupling of ε-near-zero and surface plasmon polariton modes. Phys. Rev. B 2017, 96, 075415. [Google Scholar] [CrossRef] [Green Version]
- Moncada-Villa, E.; Oliveira, O.N., Jr.; Mejía-Salazar, J.R. ε-Near-Zero Materials for Highly Miniaturizable Magnetoplasmonic Sensing Devices. J. Phys. Chem. C 2019, 123, 3790. [Google Scholar] [CrossRef]
- Onbasli, M.C.; Beran, L.; Zahradník, M.; Kučera, M.; Antoš, R.; Mistrík, J.; Dionne, G.F.; Veis, M.; Ross, C.A. Optical and magneto-optical behavior of Cerium Yttrium Iron Garnet thin films at wavelengths of 200–1770 nm. Sci. Rep. 2016, 6, 23640. [Google Scholar] [CrossRef] [Green Version]
- Bi, L.; Hu, J.; Jiang, P.; Kim, H.S.; Kim, D.H.; Onbasli, M.C.; Dionne, G.F.; Ross, C.A. Magneto-Optical Thin Films for On-Chip Monolithic Integration of Non-Reciprocal Photonic Devices. Materials 2013, 6, 5094–5117. [Google Scholar] [CrossRef] [Green Version]
- Onbasli, M.C.; Goto, T.; Sun, X.; Huynh, N.; Ross, C.A. Integration of bulk-quality thin film magneto-optical cerium-doped yttrium iron garnet on silicon nitride photonic substrates. Opt. Exp. 2014, 22, 25183–25192. [Google Scholar] [CrossRef]
- Papadakis, G.T.; Davoyan, A.; Yeh, P.; Atwater, H. Mimicking surface polaritons for unpolarized light with high-permittivity materials. Phys. Rev. Mat. 2019, 3, 015202. [Google Scholar] [CrossRef]
- Caballero, B.; García-Martín, A.; Cuevas, J.C. Generalized scattering-matrix approach for magneto-optics in periodically patterned multilayer systems. Phys. Rev. B 2012, 85, 245103. [Google Scholar] [CrossRef] [Green Version]
- Markoš, P.; Soukoulis, C. Wave Propagation: From Electronos to Photonic Crystals and Left-Handed Materials; Princeton Univ. Press: Princeton, NJ, USA, 2008; p. 212. [Google Scholar]
- Maksymov, I.S.; Hutomo, J.; Kostylev, M. Transverse magneto-optical Kerr effect in subwavelength dielectric gratings. Opt. Exp. 2014, 22, 8720. [Google Scholar] [CrossRef] [PubMed]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moncada-Villa, E.; Mejía-Salazar, J.R. High-Refractive-Index Materials for Giant Enhancement of the Transverse Magneto-Optical Kerr Effect. Sensors 2020, 20, 952. https://doi.org/10.3390/s20040952
Moncada-Villa E, Mejía-Salazar JR. High-Refractive-Index Materials for Giant Enhancement of the Transverse Magneto-Optical Kerr Effect. Sensors. 2020; 20(4):952. https://doi.org/10.3390/s20040952
Chicago/Turabian StyleMoncada-Villa, Edwin, and J. Ricardo Mejía-Salazar. 2020. "High-Refractive-Index Materials for Giant Enhancement of the Transverse Magneto-Optical Kerr Effect" Sensors 20, no. 4: 952. https://doi.org/10.3390/s20040952




