Self-Supervised Point Set Local Descriptors for Point Cloud Registration
Abstract
1. Introduction
- We propose a self-supervised method to learn point cloud descriptors requiring no manual annotation and selection during training.
- We propose a keypoint sampling manner during training, which can focus on interesting points and further boost the performance.
- Experiments show that our self-supervised learned local descriptor has better performance than the supervised 3DFeatNet.
2. Related Work
2.1. Registration Model
2.2. Descriptors
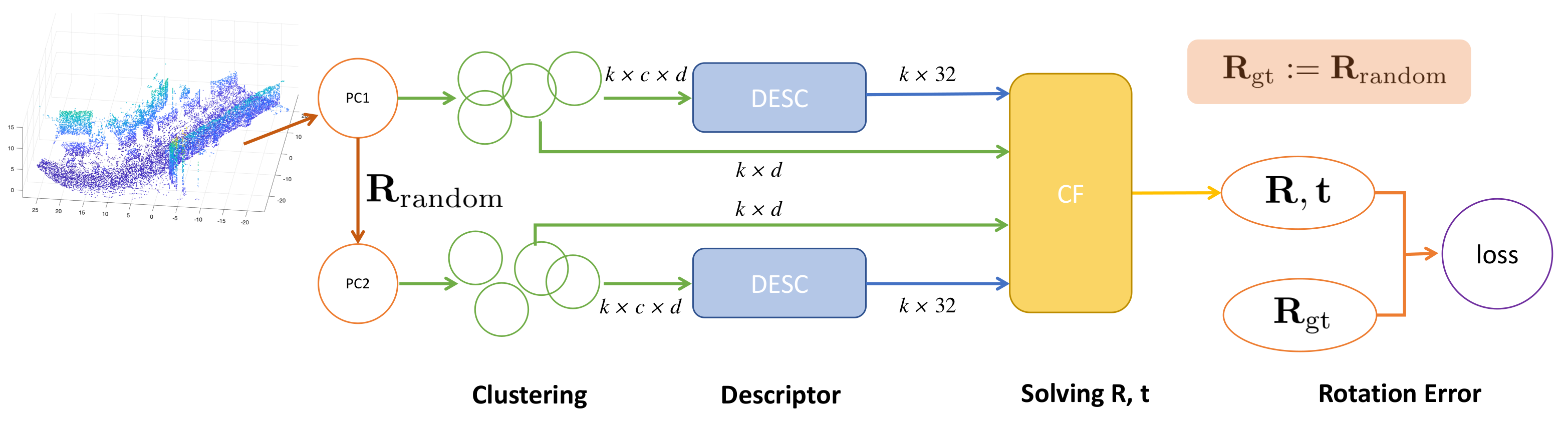
3. Method
3.1. The Registration Layer
3.2. Keypoint Sampling
3.3. Network Architecture
4. Experiment
4.1. Datasets
4.1.1. Oxford RobotCar Dataset
4.1.2. KITTI Dataset
4.2. Setting
4.3. Precision Test
4.4. Geometric Registration
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. CF Registration Model
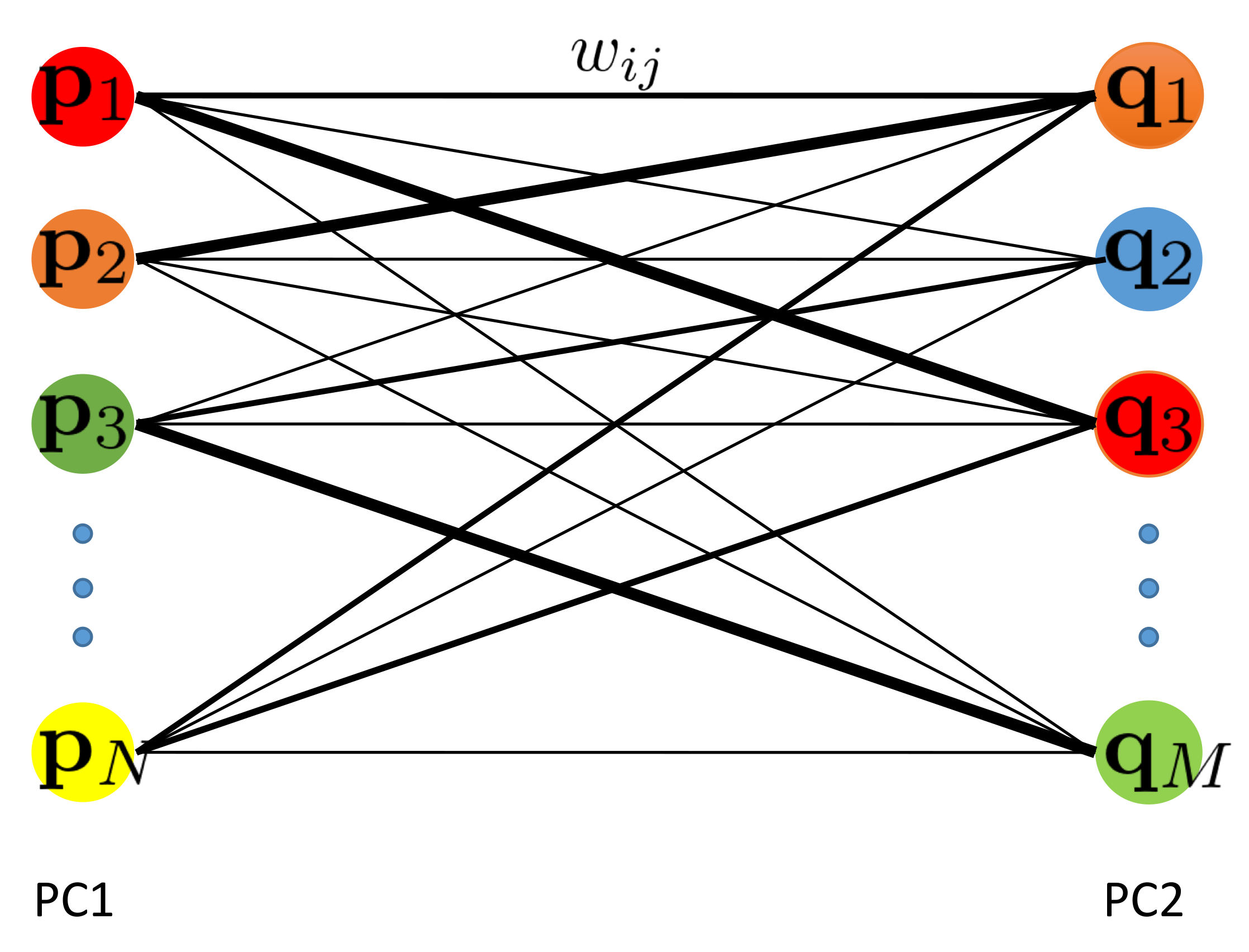
Appendix A.1. Solving the Transformation
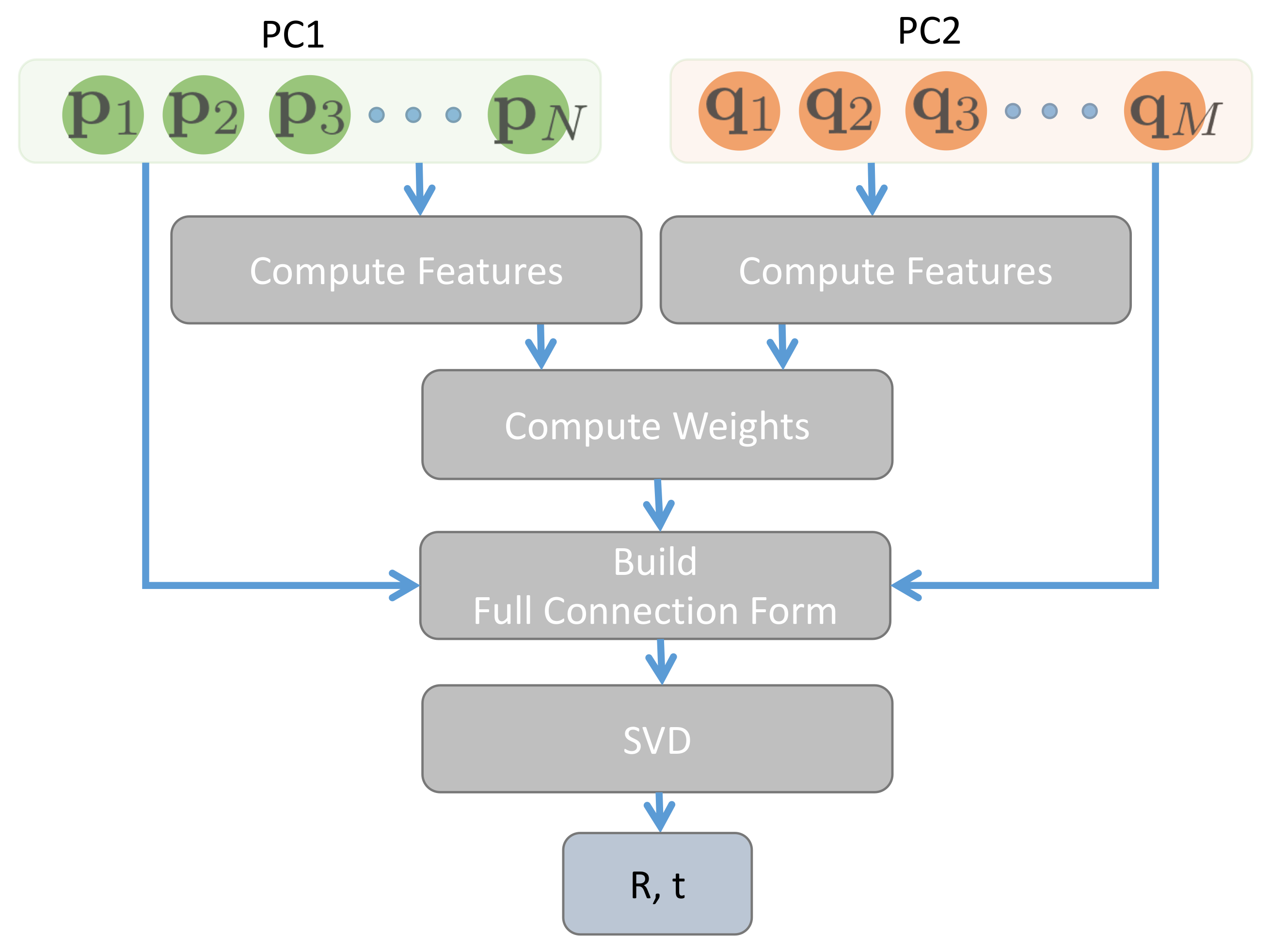
Appendix A.2. Weights as Similarity of Feature
Appendix A.3. Time Complexity
Appendix A.4. A Variant: Applying on Point Set of Keypoints
Appendix B. Experiments and Results

Appendix B.1. Settings
Appendix B.2. Sensitivity to Noise
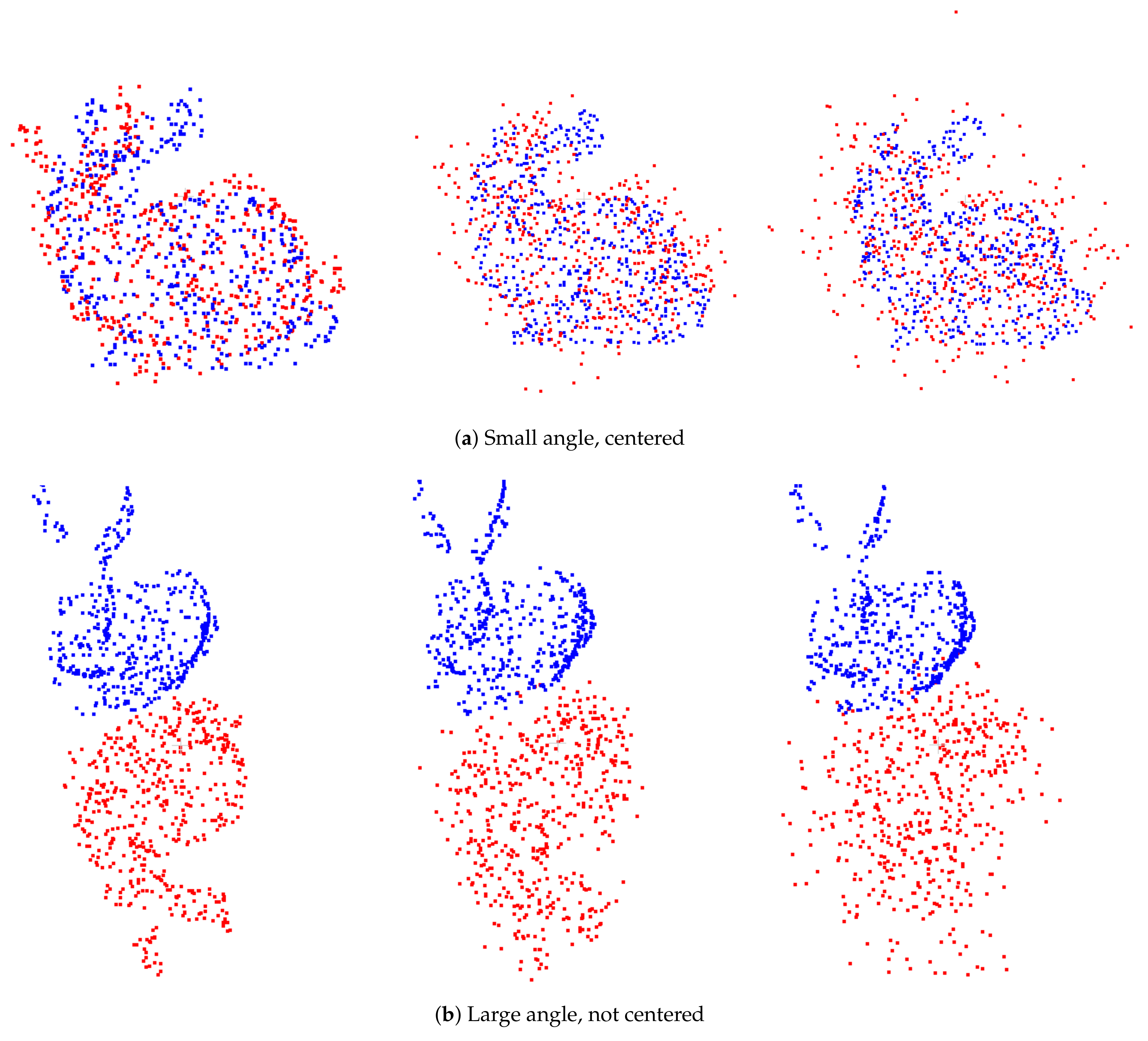
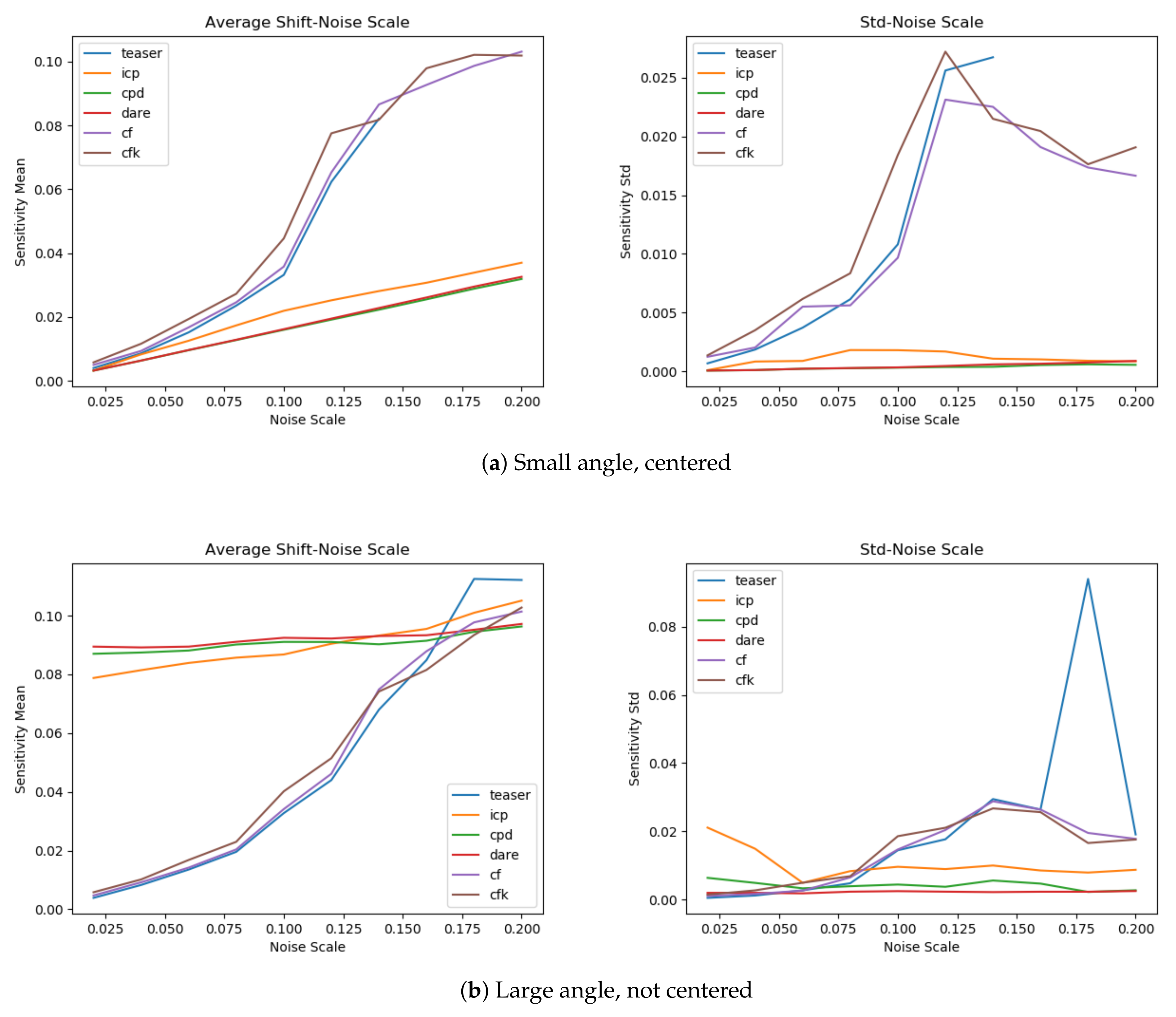
Appendix B.3 Robustness to Outliers
| Small Rotation, Centered | Large Rotation, Not Centered | |
|---|---|---|
| ICP | ||
| CPD | 2.4 × 10 ± 1.7 × 10 | |
| DARE | ||
| TEASER++ | ||
| CF | ||
| CFK |
Appendix B.4. Accuracy
| Small Rotation, Centered | Large Rotation, Not Centered | |||||
|---|---|---|---|---|---|---|
| Bunny | Dragon | Armadillo | Bunny | Dragon | Armadillo | |
| ICP | ||||||
| CPD | ||||||
| DARE | ||||||
| TEASER++ | ||||||
| CF | ||||||
| CFK | ||||||
References
- Durrant-Whyte, H.; Bailey, T. Simultaneous localization and mapping: Part I. IEEE Robot. Autom. Mag. 2006, 13, 99–110. [Google Scholar] [CrossRef]
- Nüchter, A.; Lingemann, K.; Hertzberg, J.; Surmann, H. 6D SLAM – 3D Mapping Outdoor Environments. J. Field Robot. (JFR) Spec. Issue Quant. Perform. Eval. Robot. Intell. Syst. 2007, 24, 699–722. [Google Scholar] [CrossRef]
- May, S.; Dröschel, D.; Holz, D.; Fuchs, S.; Malis, E.; Nüchter, A.; Hertzberg, J. 3D Mapping with Time-of-Flight Cameras. J. Field Robot. (JFR) Spec. Issue-Three-Dimens. Mapp. 2009, 26, 892–914. [Google Scholar] [CrossRef]
- Li, H.; Hartley, R. The 3D-3D registration problem revisited. In Proceedings of the 2007 IEEE 11th International Conference on Computer Vision, Rio de Janeiro, Brazil, 14–20 October 2007; pp. 1–8. [Google Scholar]
- Bellekens, B.; Spruyt, V.; Berkvens, R.; Weyn, M. A survey of rigid 3D pointcloud registration algorithms. In Proceedings of the AMBIENT 2014: The Fourth International Conference on Ambient Computing, Applications, Services and Technologies, Rome, Italy, 24–28 August 2014; pp. 8–13. [Google Scholar]
- Marden, S.; Guivant, J. Improving the performance of ICP for real-time applications using an approximate nearest neighbour search. In Proceedings of the Australasian Conference on Robotics and Automation, Wellington, New Zealand, 3–5 December 2012; pp. 3–5. [Google Scholar]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. Sensor Fusion IV: Control Paradigms and Data Structures. Int. Soc. Opt. Photonics 1992, 1611, 586–607. [Google Scholar]
- Fantoni, S.; Castellani, U.; Fusiello, A. Accurate and automatic alignment of range surfaces. In Proceedings of the 2012 Second International Conference on 3D Imaging, Modeling, Processing, Visualization & Transmission, Zurich, Switzerland, 13–15 October 2012; pp. 73–80. [Google Scholar]
- Segal, A.; Haehnel, D.; Thrun, S. Generalized-icp. Robot. Sci. Syst. 2009, 2, 435. [Google Scholar]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast point feature histograms (FPFH) for 3D registration. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar]
- Tsin, Y.; Kanade, T. A correlation-based approach to robust point set registration. In Proceedings of the European Conference on Computer Visio, Prague, Czech Republic, 11–14 May 2014; Springer: Berlin/Heidelberg, Germany, 2004; pp. 558–569. [Google Scholar]
- Myronenko, A.; Song, X. Point set registration: Coherent point drift. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2262–2275. [Google Scholar] [CrossRef] [PubMed]
- Zheng, B.; Ishikawa, R.; Oishi, T.; Takamatsu, J.; Ikeuchi, K. A fast registration method using IP and its application to ultrasound image registration. IPSJ Trans. Comput. Vis. Appl. 2009, 1, 209–219. [Google Scholar] [CrossRef]
- Rusu, R.B.; Marton, Z.C.; Blodow, N.; Beetz, M. Learning informative point classes for the acquisition of object model maps. In Proceedings of the 2008 10th International Conference on Control, Automation, Robotics and Vision, Hanoi, Vietnam, 17–20 December 2008; pp. 643–650. [Google Scholar]
- Huber, D.F.; Hebert, M. Automatic Three-Dimensional Modeling from Reality. Ph.D. Thesis, Carnegie Mellon University, Schenley Park, Pittsburgh, PA, USA, 2002. [Google Scholar]
- Tombari, F.; Salti, S.; Di Stefano, L. Unique shape context for 3D data description. In Proceedings of the ACM workshop on 3D Object Retrieval, Firenze, Italy, 25–29 October 2010; pp. 57–62. [Google Scholar]
- Barnea, S.; Filin, S. Keypoint based autonomous registration of terrestrial laser point-clouds. ISPRS J. Photogramm. Remote. Sens. 2008, 63, 19–35. [Google Scholar] [CrossRef]
- Steder, B.; Grisetti, G.; Burgard, W. Robust place recognition for 3D range data based on point features. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, Alaska, 3–8 May 2010; pp. 1400–1405. [Google Scholar]
- Flint, A.; Dick, A.; Van Den Hengel, A. Thrift: Local 3d structure recognition. In Proceedings of the 9th Biennial Conference of the Australian Pattern Recognition Society on Digital Image Computing Techniques and Applications (DICTA 2007), Glenelg, Australia, 3–5 December 2007; pp. 182–188. [Google Scholar]
- Wu, C.; Clipp, B.; Li, X.; Frahm, J.M.; Pollefeys, M. 3D model matching with viewpoint-invariant patches (VIP). In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Zeng, A.; Song, S.; Nießner, M.; Fisher, M.; Xiao, J.; Funkhouser, T. 3dmatch: Learning local geometric descriptors from rgb-d reconstructions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1802–1811. [Google Scholar]
- Gojcic, Z.; Zhou, C.; Wegner, J.D.; Wieser, A. The perfect match: 3d point cloud matching with smoothed densities. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5545–5554. [Google Scholar]
- Deng, H.; Birdal, T.; Ilic, S. Ppfnet: Global context aware local features for robust 3d point matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 195–205. [Google Scholar]
- Deng, H.; Birdal, T.; Ilic, S. Ppf-foldnet: Unsupervised learning of rotation invariant 3d local descriptors. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 602–618. [Google Scholar]
- Bai, X.; Luo, Z.; Zhou, L.; Fu, H.; Quan, L.; Tai, C.L. D3Feat: Joint Learning of Dense Detection and Description of 3D Local Features. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 6359–6367. [Google Scholar]
- Yew, Z.J.; Lee, G.H. 3DFeat-Net: Weakly supervised local 3D features for point cloud registration. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 630–646. [Google Scholar]
- Lu, F.; Chen, G.; Liu, Y.; Qu, Z.; Knoll, A. RSKDD-Net: Random Sample-based Keypoint Detector and Descriptor. arXiv 2020, arXiv:2010.12394. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5099–5108. [Google Scholar]
- Maddern, W.; Pascoe, G.; Linegar, C.; Newman, P. 1 year, 1000 km: The Oxford RobotCar dataset. Int. J. Robot. Res. 2017, 36, 3–15. [Google Scholar] [CrossRef]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The kitti vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Yang, H.; Shi, J.; Carlone, L. TEASER: Fast and Certifiable Point Cloud Registration. IEEE Trans. Robot. 2020. [Google Scholar] [CrossRef]
- Huang, R.; Xu, Y.; Yao, W.; Hoegner, L.; Stilla, U. Robust global registration of point clouds by closed-form solution in the frequency domain. ISPRS J. Photogramm. Remote. Sens. 2020, 171, 310–329. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 June 2017; pp. 652–660. [Google Scholar]
- Li, J.; Lee, G.H. Usip: Unsupervised stable interest point detection from 3d point clouds. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–3 November 2019; pp. 361–370. [Google Scholar]
- Fleuret, F.; Sahbi, H. Scale-invariance of support vector machines based on the triangular kernel. In Proceedings of the 3rd International Workshop on Statistical and Computational Theories of Vision, Nice, France, October 2003; pp. 1–13. [Google Scholar]
- Arun, K.S.; Huang, T.S.; Blostein, S.D. Least Square Fitting of Two 3-D Point Sets. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 9, 698–700. [Google Scholar] [CrossRef]
- Sorkine, O. Least-squares rigid motion using svd. Tech. Notes 2009, 120, 52. [Google Scholar]
- Larochelle, P.M.; Murray, A.P.; Angeles, J. A distance metric for finite sets of rigid-body displacements via the polar decomposition. J. Mech. Des. 2007, 129, 883–886. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th {USENIX} Symposium on Operating Systems Design and Implementation ({OSDI} 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Järemo Lawin, F.; Danelljan, M.; Shahbaz Khan, F.; Forssén, P.E.; Felsberg, M. Density adaptive point set registration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3829–3837. [Google Scholar]
- Cignoni, P.; Callieri, M.; Corsini, M.; Dellepiane, M.; Ganovelli, F.; Ranzuglia, G. Meshlab: An open-source mesh processing tool. In Proceedings of the Eurographics ITALIAN Chapter Conference, Salerno, Italy, 2–4 July 2008; Volume 2008, pp. 129–136. [Google Scholar]
- Rusu, R.B.; Cousins, S. 3d is here: Point cloud library (pcl). In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1–4. [Google Scholar]
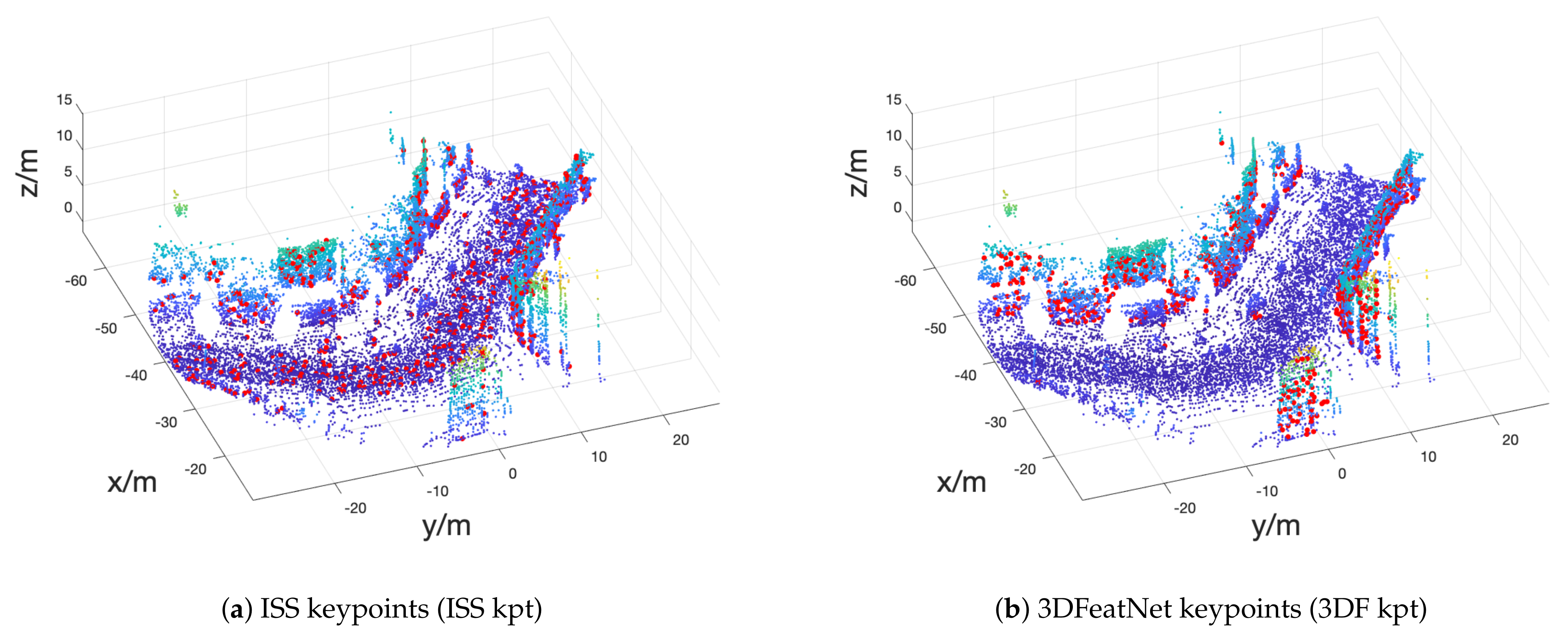

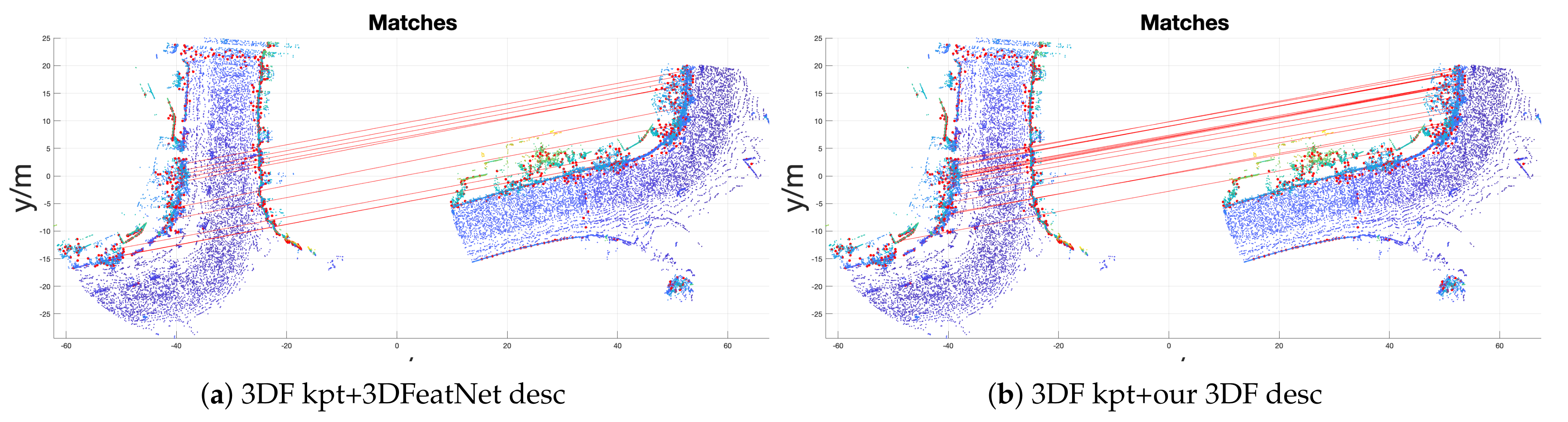
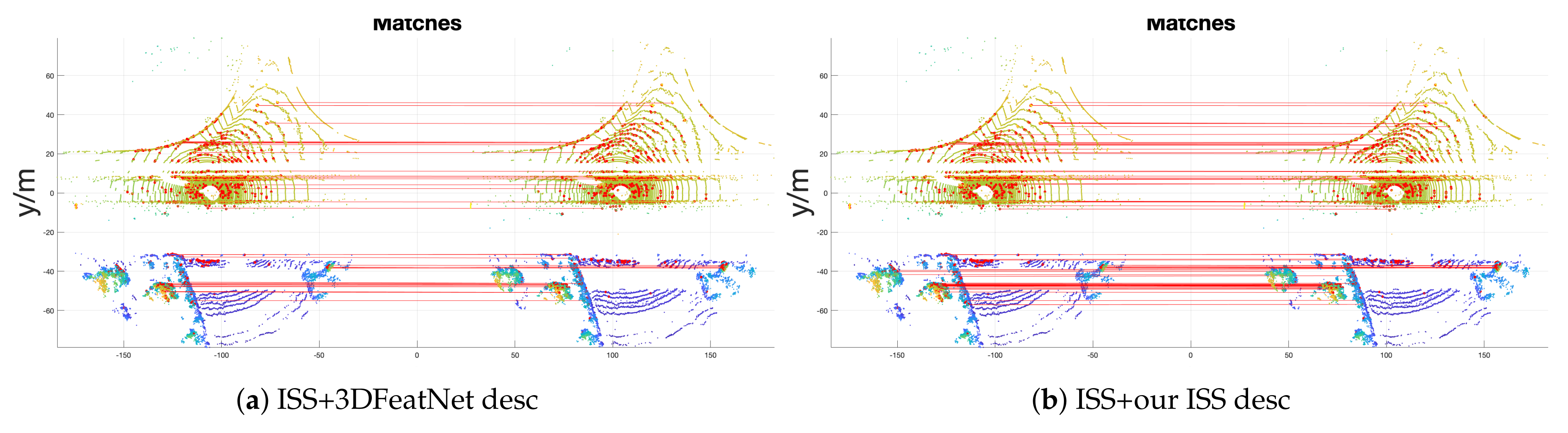
| RTE (m) | RRE () | Success Rate | Avg #Iter | |
|---|---|---|---|---|
| ISS + FPFH | 0.396 | 1.60 | 92.32% | 7171 |
| ISS + SI | 0.415 | 1.61 | 87.45% | 9888 |
| ISS + USC | 0.324 | 1.22 | 94.02% | 7084 |
| ISS + CGF | 0.431 | 1.62 | 87.36% | 9628 |
| ISS + 3DMatch | 0.494 | 1.78 | 69.06% | 9131 |
| ISS + PN++ | 0.511 | 1.88 | 48.86% | 9904 |
| ISS + 3DFeatNet desc | 0.314 | 1.08 | 97.66% | 7127 |
| 3DFeatNet kpt + 3DFeatNet desc | 0.300 | 1.07 | 98.10% | 2940 |
| ISS + 3DFeatNet desc | 0.314 | 1.08 | 97.66% | 7126 |
| ISS + our desc | 0.311 | 1.01 | 98.10% | 5648 |
| ISS + our ISS desc | 0.311 | 1.00 | 98.23% | 5545 |
| 3DF kpt + 3DFeatNet desc | 0.304 | 1.08 | 97.66% | 3294 |
| 3DF kpt + our desc | 0.310 | 1.08 | 97.05% | 3650 |
| 3DF kpt + our 3DF desc | 0.298 | 1.02 | 97.90% | 2703 |
| RTE (m) | RRE () | Success Rate | Avg #Iter | |
|---|---|---|---|---|
| ISS + FPFH | 0.325 | 1.08 | 58.59% | 7462 |
| ISS + SI | 0.358 | 1.17 | 55.92% | 9219 |
| ISS + USC | 0.262 | 0.83 | 78.24% | 7873 |
| ISS + CGF | 0.233 | 0.69 | 87.81% | 7442 |
| ISS + 3DMatch | 0.283 | 0.79 | 89.12% | 7292 |
| 3DF kpt + 3DFeatNet desc | 0.258 | 0.57 | 95.97% | 3798 |
| ISS + 3DFeatNet desc | 0.246 | 0.627 | 93.50% | 8311 |
| 3DF kpt + 3DFeatNet desc | 0.264 | 0.599 | 95.58% | 4394 |
| ISS + our desc | 0.215 | 0.510 | 93.50% | 5960 |
| ISS + our ISS desc | 0.215 | 0.459 | 93.85% | 4356 |
| 3DF kpt + our desc | 0.258 | 0.570 | 95.44% | 3732 |
| 3DF kpt + our 3DF kpt | 0.244 | 0.501 | 95.87% | 2631 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Y.; Borrmann, D.; Hou, J.; Ma, Y.; Nüchter, A.; Schwertfeger, S. Self-Supervised Point Set Local Descriptors for Point Cloud Registration. Sensors 2021, 21, 486. https://doi.org/10.3390/s21020486
Yuan Y, Borrmann D, Hou J, Ma Y, Nüchter A, Schwertfeger S. Self-Supervised Point Set Local Descriptors for Point Cloud Registration. Sensors. 2021; 21(2):486. https://doi.org/10.3390/s21020486
Chicago/Turabian StyleYuan, Yijun, Dorit Borrmann, Jiawei Hou, Yuexin Ma, Andreas Nüchter, and Sören Schwertfeger. 2021. "Self-Supervised Point Set Local Descriptors for Point Cloud Registration" Sensors 21, no. 2: 486. https://doi.org/10.3390/s21020486
APA StyleYuan, Y., Borrmann, D., Hou, J., Ma, Y., Nüchter, A., & Schwertfeger, S. (2021). Self-Supervised Point Set Local Descriptors for Point Cloud Registration. Sensors, 21(2), 486. https://doi.org/10.3390/s21020486







