Research on Control Method of the Power System of Stepping-Type Anchoring Equipment
Abstract
:1. Introduction
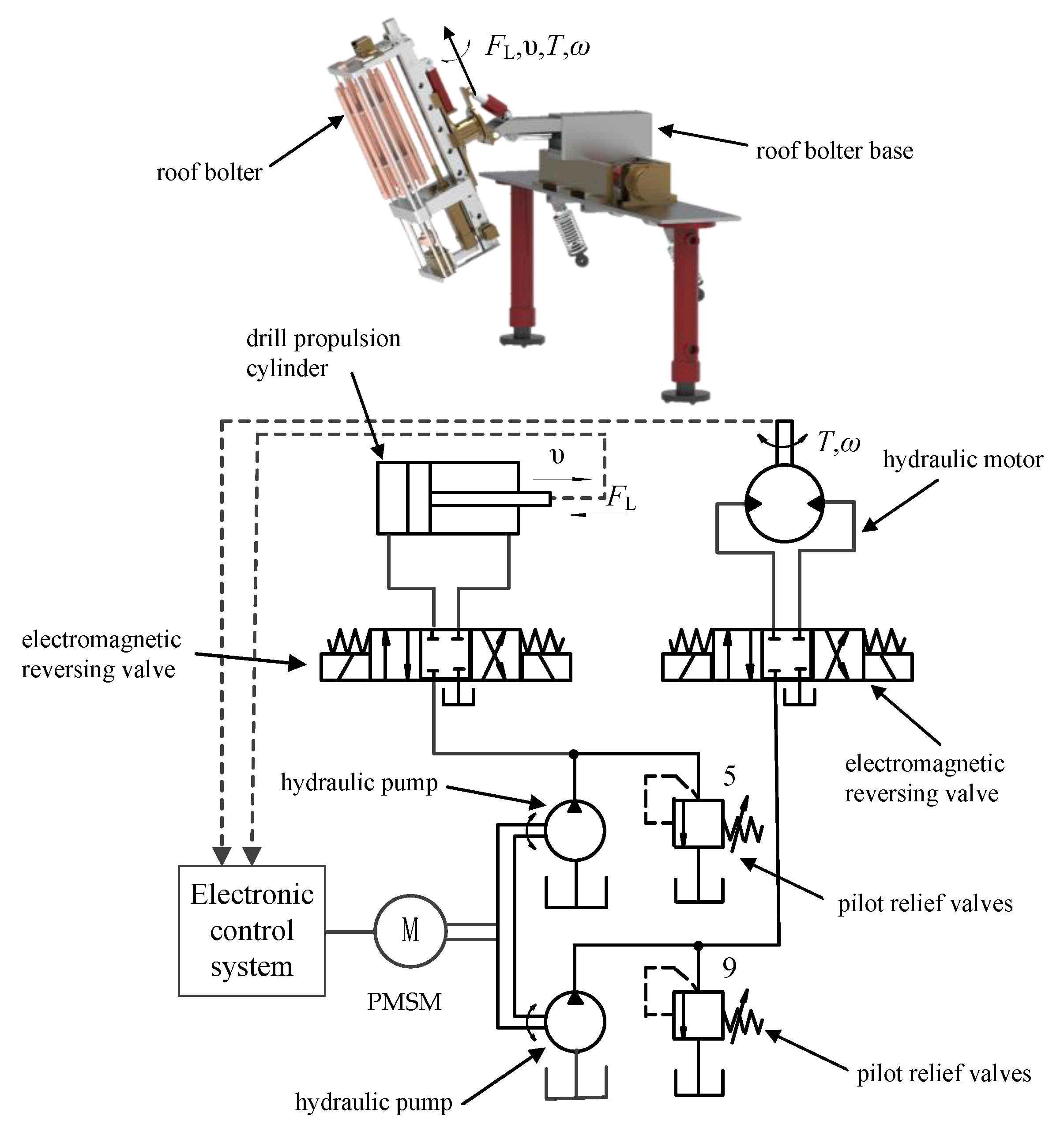
2. Stepping-Type Anchoring Equipment and Power System Composition
3. Mathematical Model of Stepping-Type Anchoring Equipment Power System
3.1. Mathematical Model of Permanent Magnet Synchronous Motor
3.2. Mathematical Model of Hydraulic System and Its Load
4. Research on the Control Method of Power System of Stepping-Type Anchoring Equipment
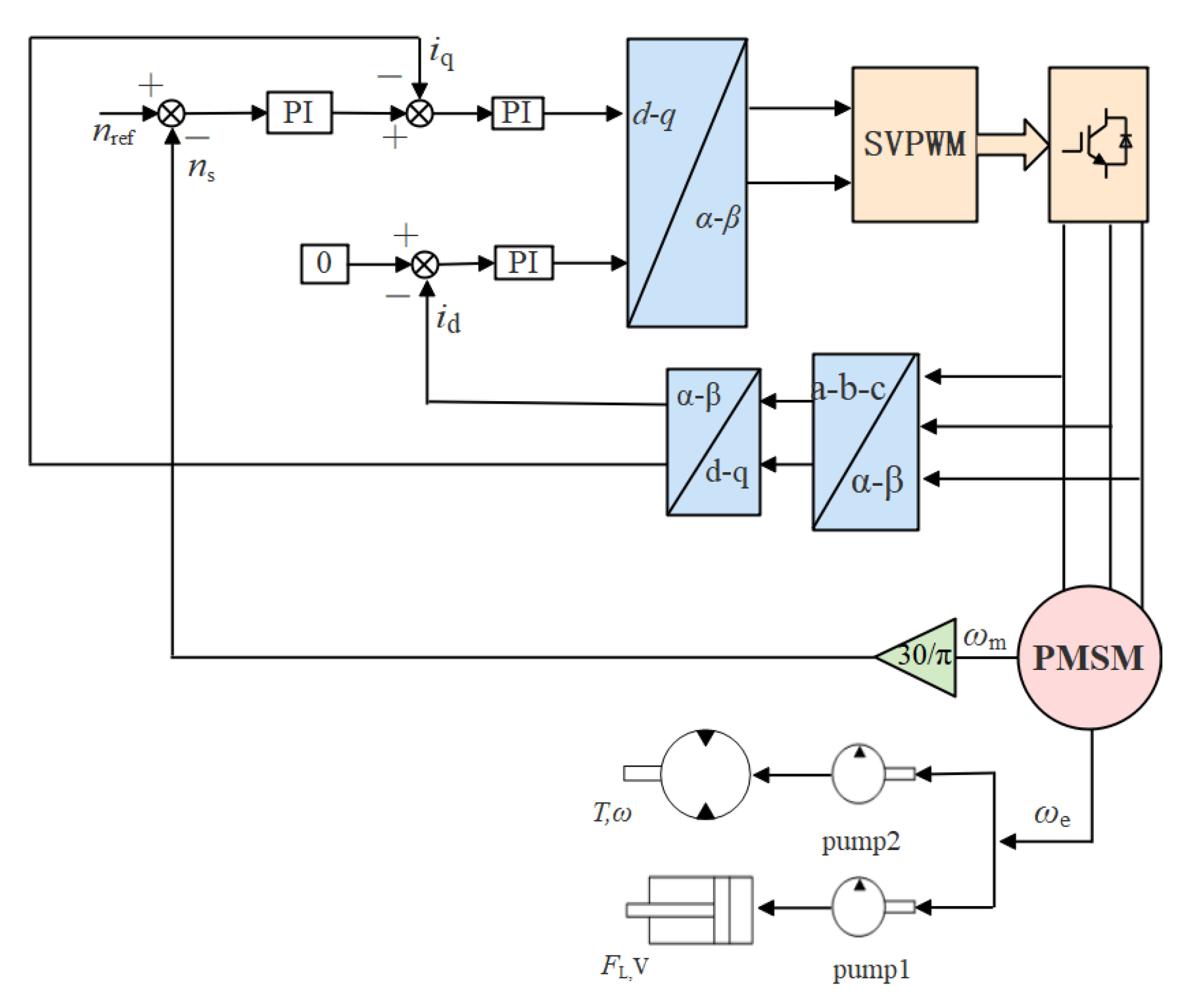
4.1. PI Control of Pump-Controlled Hydraulic System
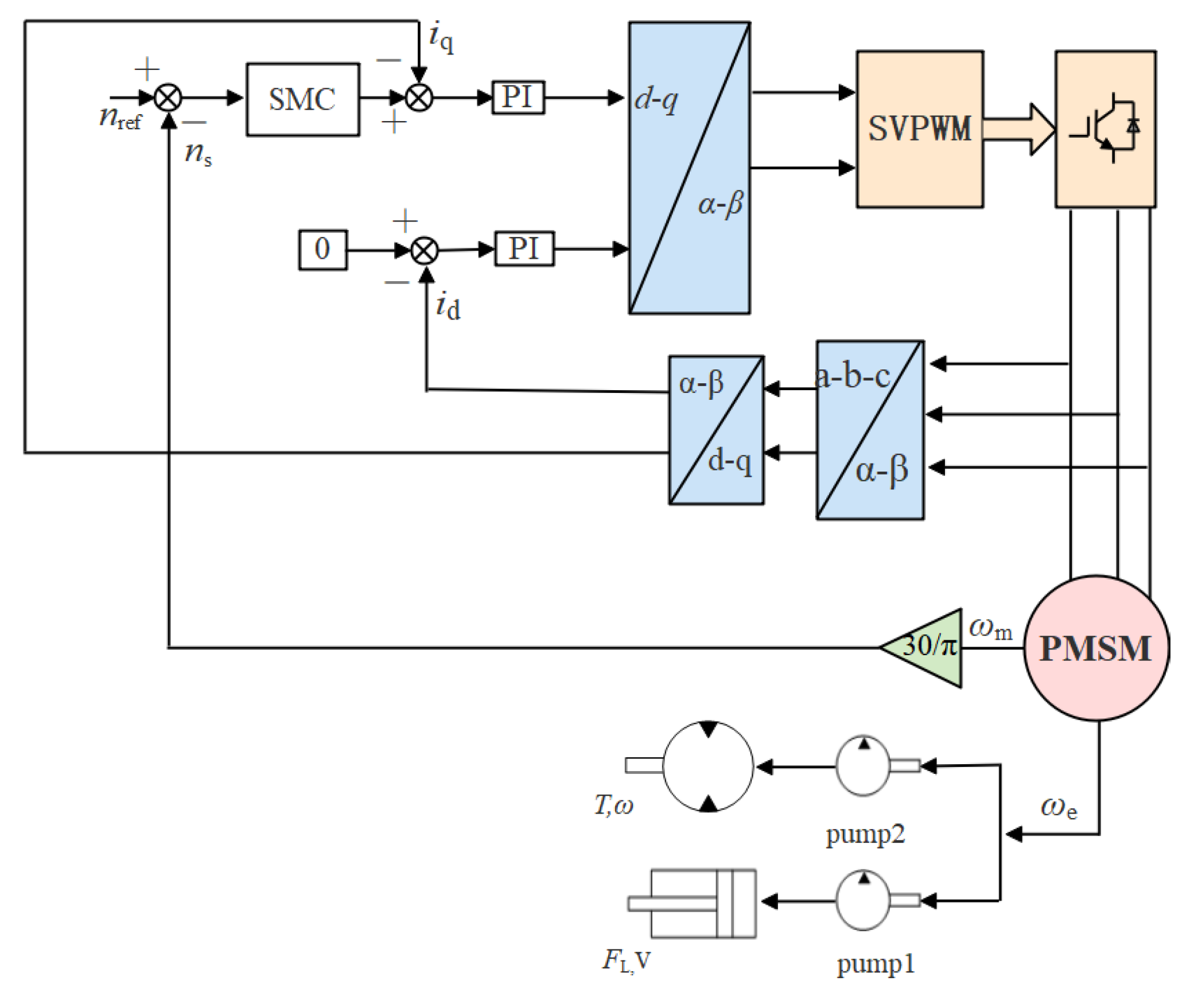
4.2. Sliding Mode Control of Pump-Controlled Hydraulic System
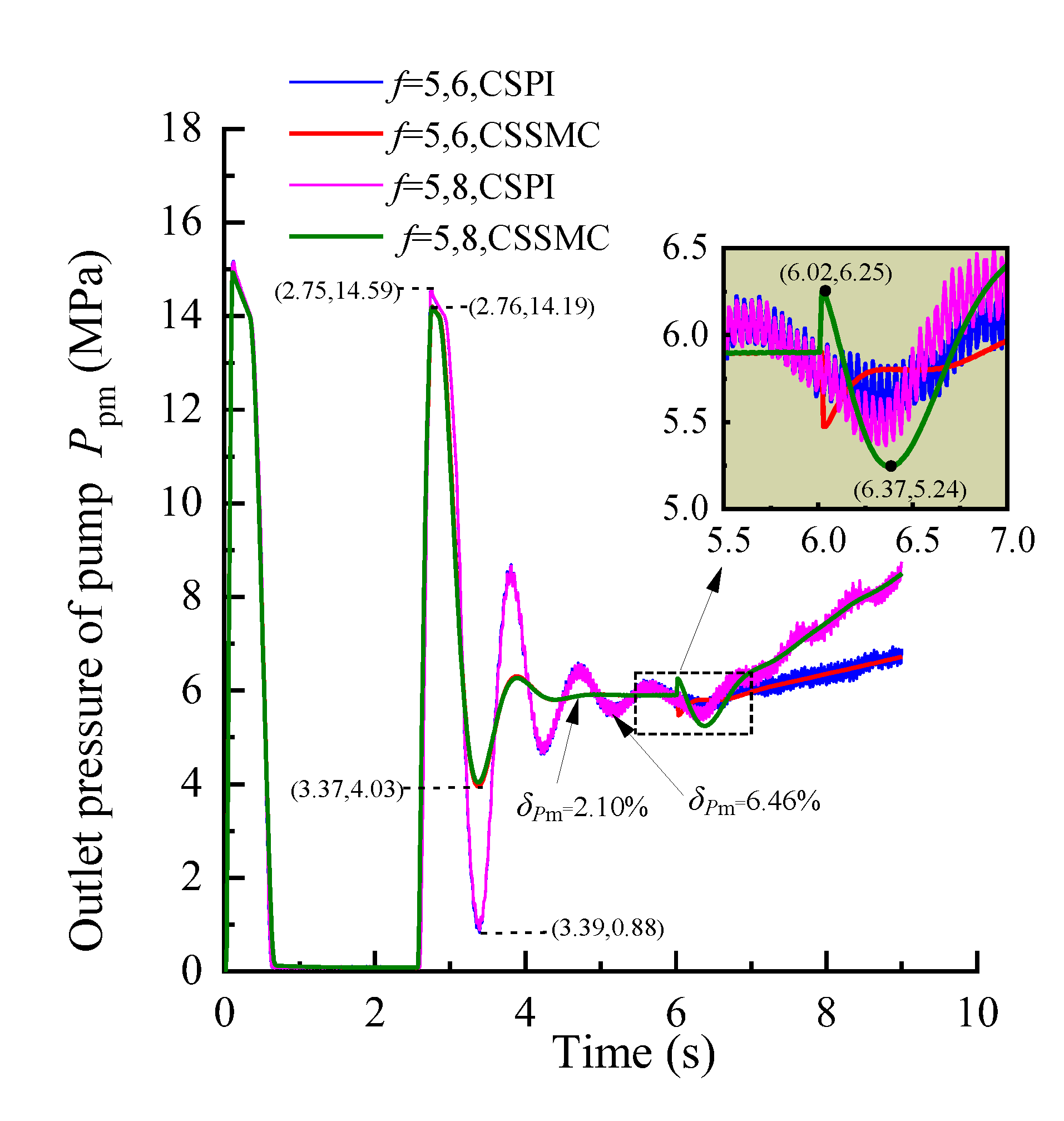
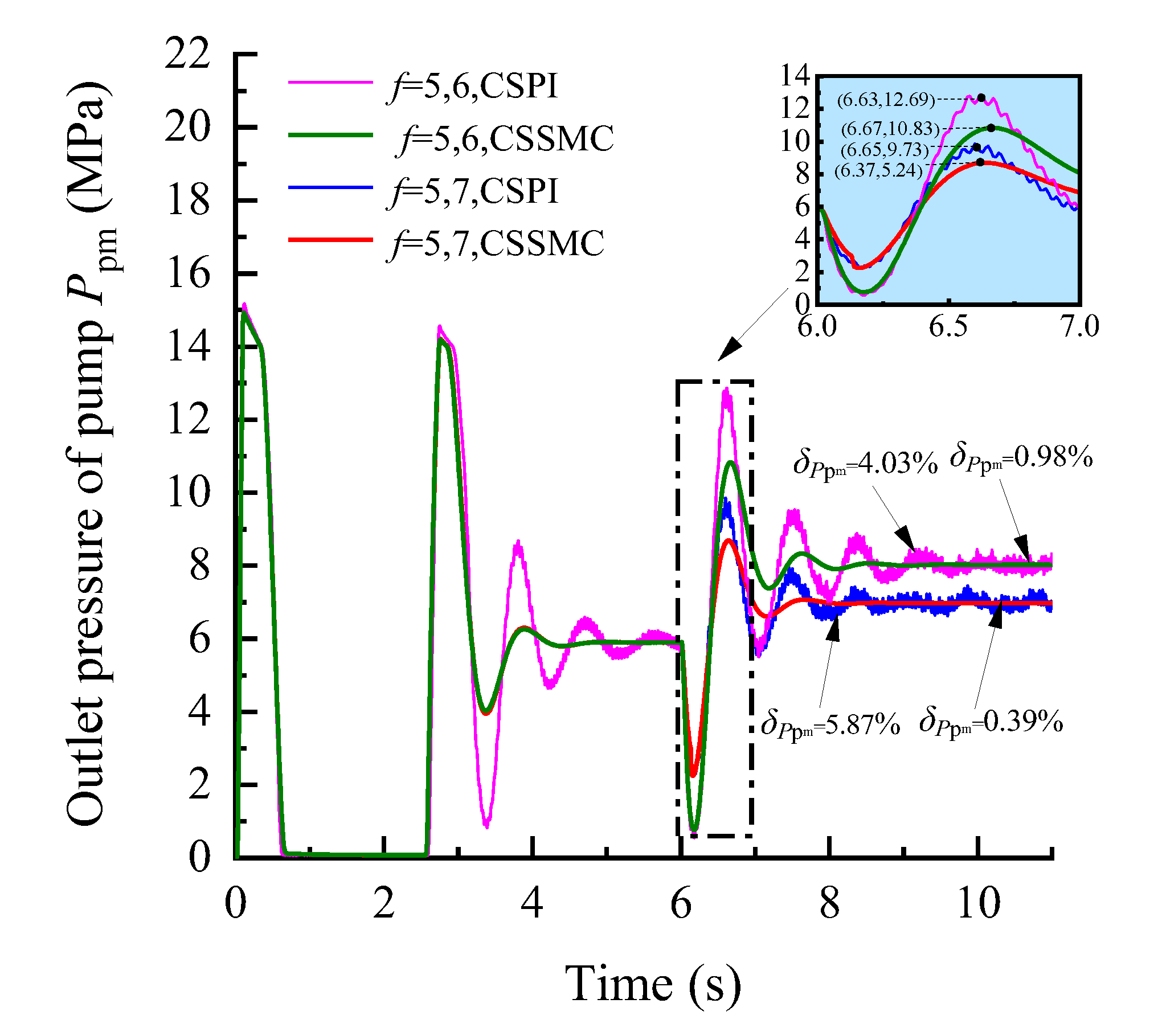
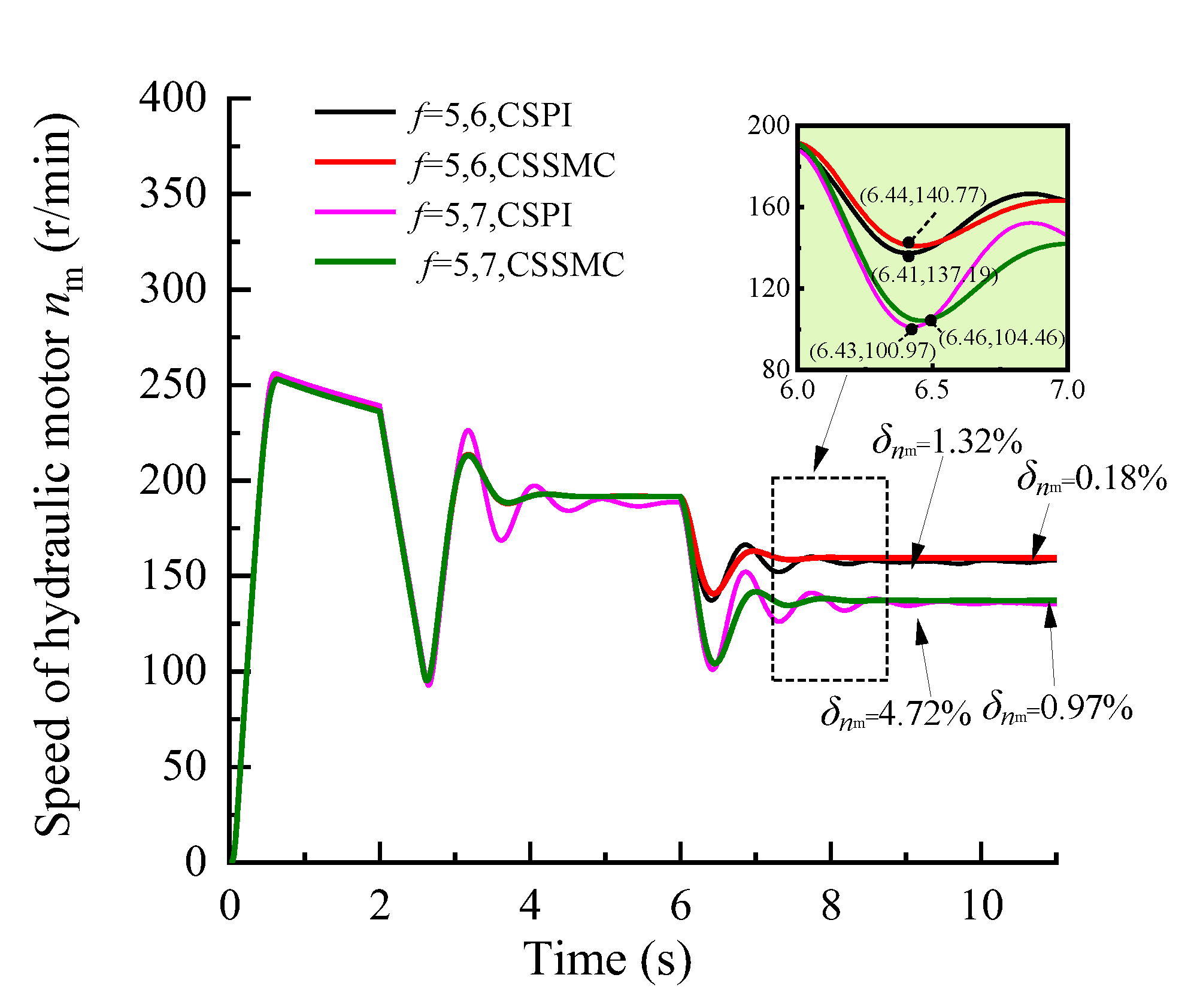
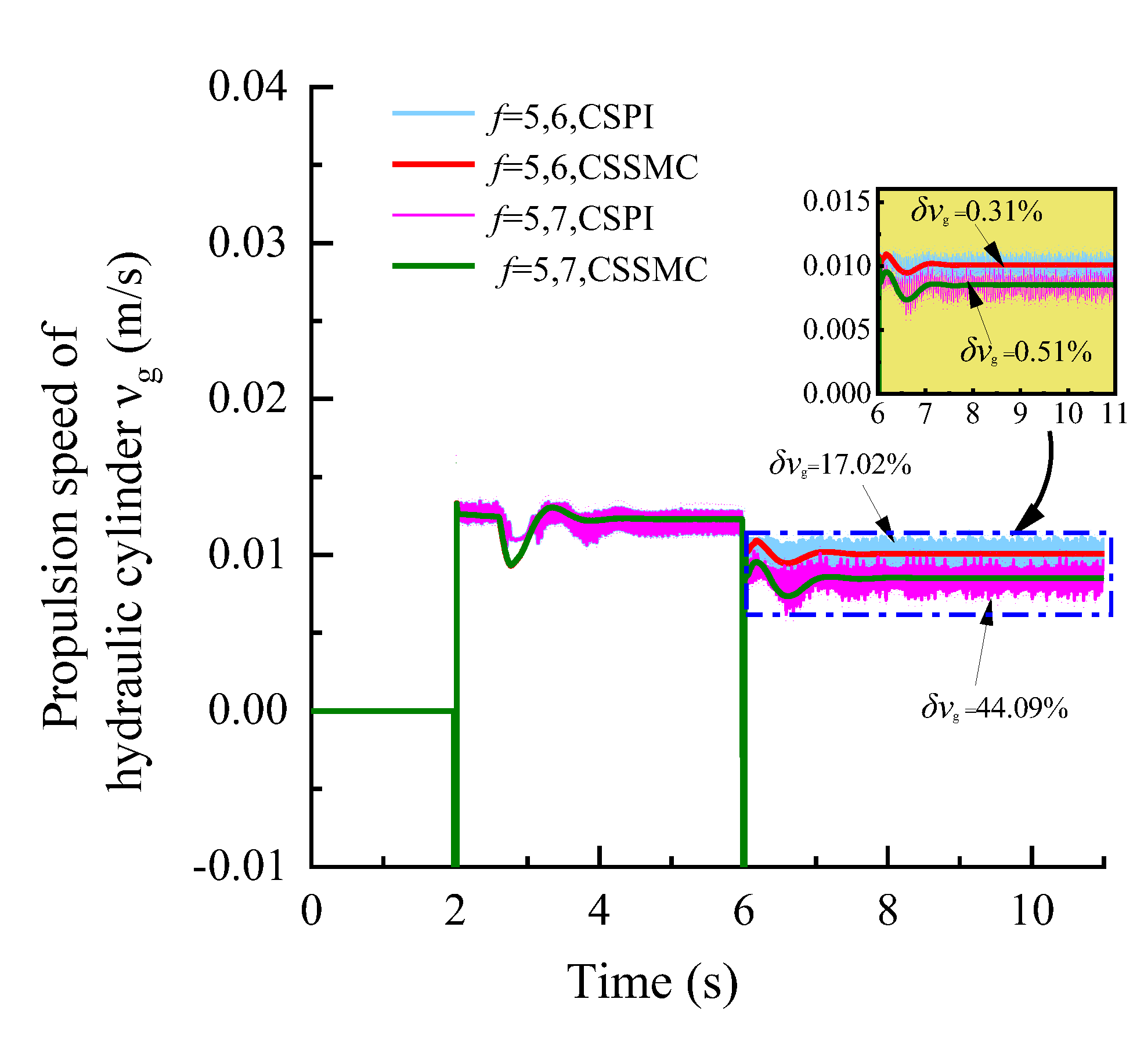
4.3. Experimental Simulation and Analysis
5. Performance Improvement Analysis of the Power Control System of Stepping-Type Anchoring Equipment
5.1. Harmonic Suppression Compensation Coordinated Control of Permanent Magnet Synchronous Motor
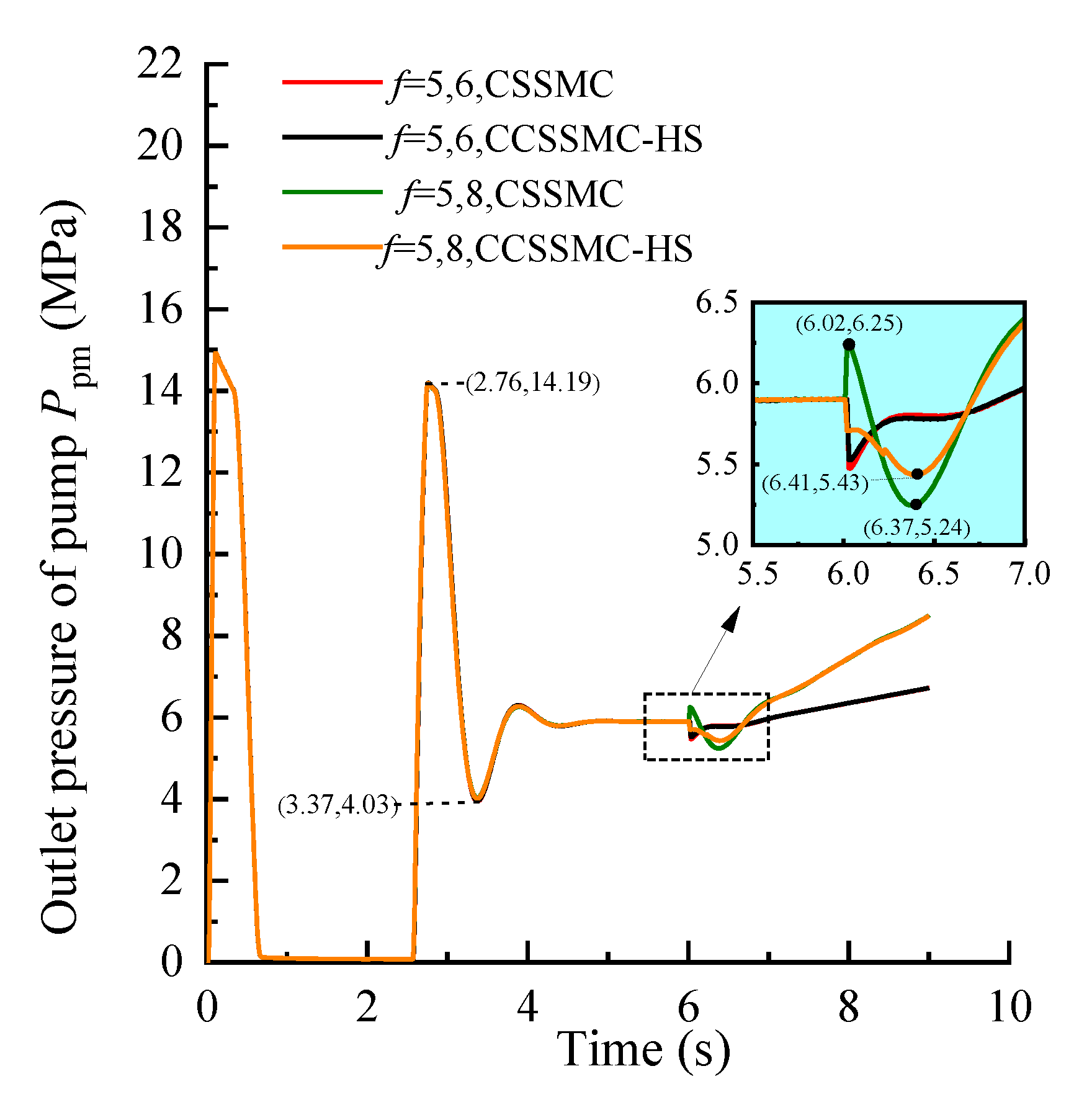
5.2. Control Method Improvement Results and Analysis
6. Conclusions
- (1)
- Following the pump control mechanism of PMSM and the system theory of interaction between anchoring equipment and coal rocks, a mathematical model of the power control system of step-type anchoring equipment was established, and the influence of coal rock hardness factor f on the stability of the power system of the anchoring equipment was analyzed.
- (2)
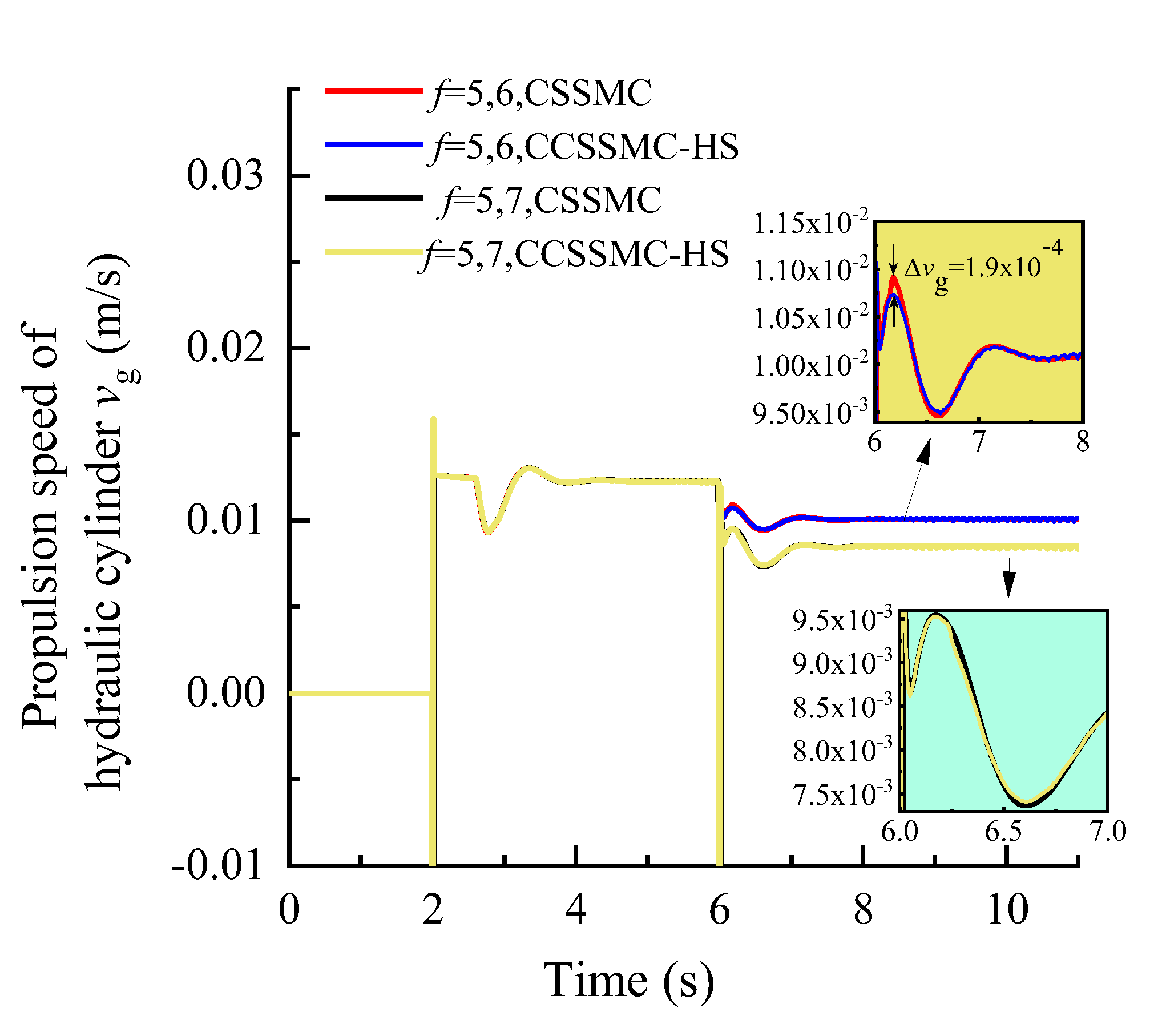
- A control strategy applicable to the drive system of walking anchoring equipment based on the CSSMC was also proposed. Compared with the CSPI, the dynamic characteristics of the hydraulic pump outlet pressure, hydraulic motor output speed, and pump-controlled hydraulic cylinder advance speed in the pump-controlled motor hydraulic circuit of this control method were greatly improved, while the maximum pulsation coefficient of each variable after the system entered the steady state was less than 3%.
- (3)
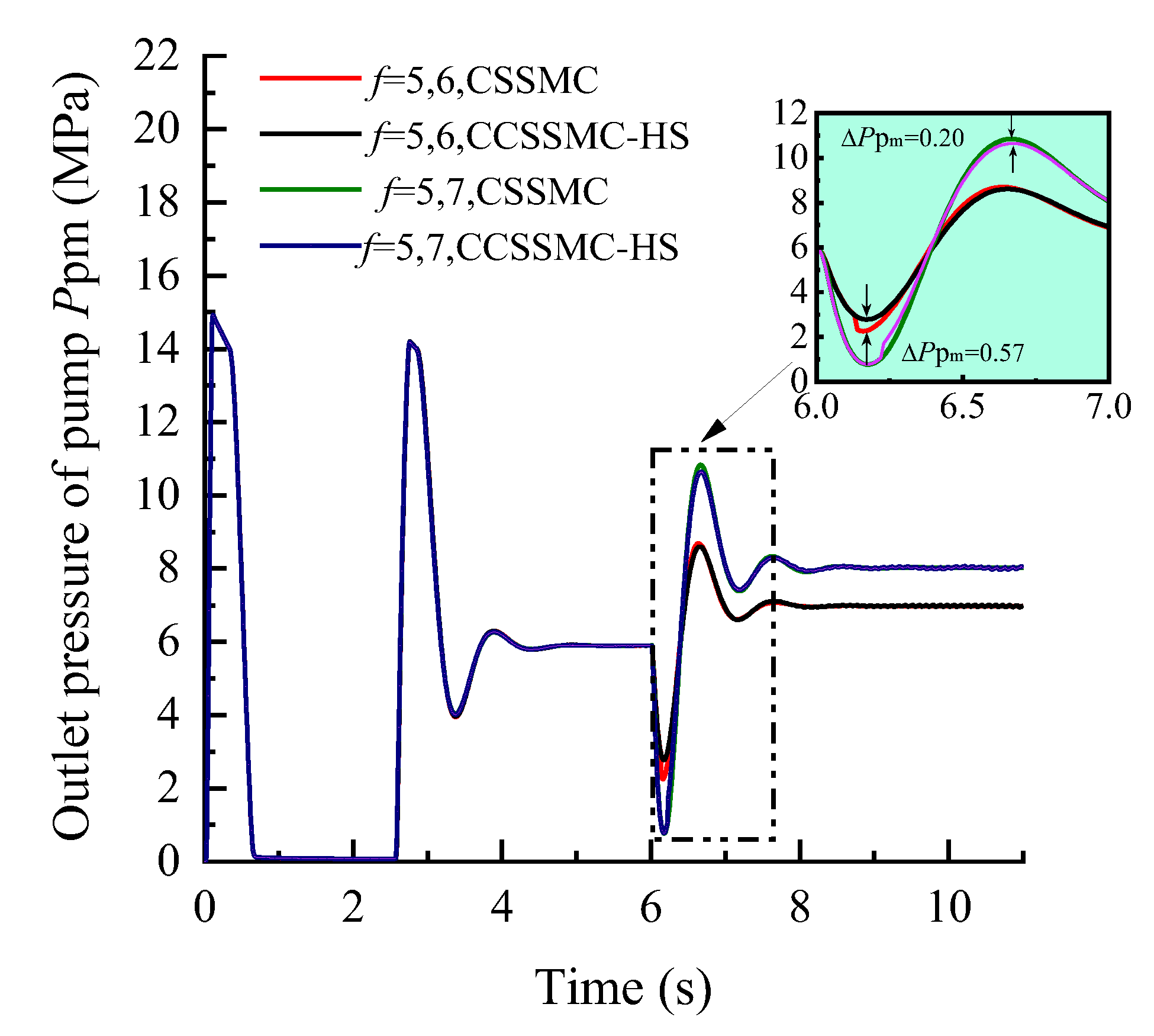
- Furthermore, the CSSMC was optimized by suppressing and compensating the harmonic components of PMSM in the power system. For the CSSMC-HS, when the coefficient of coal and rock hardness in action gradually changed from f = 5 to f = 8 and abruptly changed from f = 5 to f = 6, the hydraulic pump outlet pressure overshoot fell from 11.19% to 7.97% and from 61.19% to 52.88%, respectively, compared to the levels prior to optimization. This optimized control strategy was therefore able to mitigate the impact of load disturbance on the system’s performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, H.; Wang, J.L.; Zhang, X.F. Theory and technology of efficient roadway advance with driving and bolting integration. J. China Coal Soc. 2020, 45, 2021–2030. [Google Scholar]
- Kang, H.P. Support technologies for deep and complex roadways in underground coal mines: A review. Int. J. Coal Sci. Technol. 2014, 1, 261–277. [Google Scholar] [CrossRef] [Green Version]
- Witek, J.; Szurgacz, D. The identification of the damage causes of the hydraulic control system components in powered roof support by means of tests and calculations. In Proceedings of the 2nd International Conference on Materials Engineering & Science (Iconmeas 2019), Baghdad, Iraq, 25–26 September 2019. [Google Scholar]
- Szurgacz, D.; Przylibski, T.A.; Kasza, D. Analysis characteristics determination of electrohydraulic control system operation to reduce the operation time of a powered roof support. Proc. E3S Web Conf. 2018, 29, 00007. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Shang, M.; Ma, G. An Electro-hydraulic System on Anti-sticking for the Drilling Rig Underground Coal Mine. In Proceedings of the 2019 IEEE 8th International Conference on Fluid Power and Mechatronics (FPM), Wuhan, China, 10–13 April 2019. [Google Scholar]
- Angue, M.H. Feedback Linearization-Based Position Control of an Electrohydraulic Servo System with Supply Pressure Uncertainty. IEEE Trans. Control Syst. Technol. 2012, 20, 1092–1099. [Google Scholar] [CrossRef]
- Wos, P.; Dindorf, R. Self-tuning controllers based on polynomial methods for electro-hydraulic servo drive. In Proceedings of the AIP Conference Proceedings, Bydgoszcz, Poland, 1–7 February 2019. [Google Scholar]
- Suresh, J.; Nibras, A.; Chandresh, V.; Rabih, Y. Case Study of Intelligent Completion with New Generation Electro-Hydraulic Downhole Control System. In Proceedings of the SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, Dammam, Saudi Arabia, 25–28 April 2016. [Google Scholar] [CrossRef]
- Sidhom, L.; Chihi, I.; Sahraoui, S.; Abdelkrim, A. Intelligent-PI controller for electro-hydraulic system. In Proceedings of the 2016 4th International Conference on Control Engineering & Information Technology (CEIT), Hammamet, Tunisia, 16–18 December 2016. [Google Scholar]
- Hui, W.; Choi, C.H. Design of Control System for Hydraulic Cylinders of a Sluice Gate Using Fuzzy PI Algorithm. J. Korean Inst. Intell. Syst. 2010, 20, 109–115. [Google Scholar]
- Qin, Z.B.; Chen, F.F.; Jin, B.; Zhang, L.L. PID auto-tuning method for spool position control of electro-hydraulic proportional valve. J. Zhejiang Univ. Eng. Sci. 2015, 49, 1503–1508, 1528. [Google Scholar]
- Wrat, G.; Bhola, M.; Ranjan, P.; Mishra, S.; Das, J. Energy saving and Fuzzy-PID position control of electro-hydraulic system by leakage compensation through proportional flow control valve. ISA Trans. 2020, 101, 269–280. [Google Scholar] [CrossRef]
- Mishra, J.; Yu, X. On Fixed-Time Convergent Sliding Mode Control Design and Applications. In Emerging Trends in Sliding Mode Control; Springer: Singapore, 2021; pp. 203–237. [Google Scholar]
- Hoang, Q.D.; Lee, S.G.; Dugarjav, B. Super-Twisting Observer-Based Integral Sliding Mode Control for Tracking the Rapid Acceleration of a Piston in a Hybrid Electro-Hydraulic and Pneumatic System. Asian J. Control 2018, 21, 483–498. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.I.; Fu, L.C. Smooth sliding mode tracking control of the Stewart platform. In Proceedings of the 2005 IEEE International Conference on Control Applications (CCA’05), Toronto, ON, Canada, 28–31 August 2005; pp. 43–48. [Google Scholar]
- Lee, T.; Lee, D.; Song, B.; Baek, Y.S. Design and Control of a Polycentric Knee Exoskeleton Using an Electro-Hydraulic Actuator. Sensor 2020, 20, 211. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Malrait, F.; Jebai, A.K.; Ejjabraoui, K. Power conversion optimization for hydraulic systems controlled by variable speed drives. J. Process Control. 2019, 74, 133–146. [Google Scholar] [CrossRef]
- Gu, L.; Shi, Y. Online Monitoring Technique of Power Condition for Inverter-Fed Motor Driven Hydraulic System. Math. Proc. Camb. 2019, 2019, 1–16. [Google Scholar] [CrossRef]
- Yang, J.J.; Zhang, Q.; Wang, C.; Chang, B.S.; Wang, X.L.; Ge, S.R.; Wu, M. Status and development of robotization research on roadheader for coal mines. J. China Coal Soc. 2020, 45, 2995–3005. [Google Scholar]
- Wang, H. Present Status and Development of Mine Roadway Heading Technology and Equipment in China Coal Mine. Coal Sci. Technol. 2010, 8, 57–62. [Google Scholar]
- Guo, Y.N.; Cheng, W.; Gong, D.W.; Zhang, Y.; Xue, G.H. Adaptively robust rotary speed control of an anchorhole driller under varied surrounding rock environments. Control. Eng. Pract. 2019, 86, 24–36. [Google Scholar] [CrossRef]
- Wang, X.Y. Intelligent Integration Optimization Algorithm of PID Parameters Setting and Application for Hydraulic Control System of Rotary Impact Jumbolter. Coal Mine Mach. 2016, 37, 124–127. [Google Scholar]
- Luan, L.J.; Zhao, H.M.; Pan, D.W. Supporting Force Control Strategy of Advanced Supporting Equipment. Control Eng. China 2016, 23, 1504–1509. [Google Scholar]
- Ahn, K.K.; Dinh, Q.T. Self-tuning of quantitative feedback theory for force control of an electro-hydraulic test machine. Control Eng. Pract. 2009, 17, 1291–1306. [Google Scholar] [CrossRef]
- Wang, X.Y. Research on Hydraulic Control System of Jumbolter Based on Intelligent Fusion Optimization Algorithm. Mach. Tool Hydraul. 2017, 45, 79–82. [Google Scholar]
- Hoang, Q.D.; Rosas-Cervantes, V.A.; Lee, S.G.; Weon, L.S.; Choi, J.H.; Kwon, Y.H. Robust Finite-Time Convergence Control Mechanism for High-Precision Tracking in a Hybrid Fluid Power Actuator. IEEE Access 2020, 8, 196775–196789. [Google Scholar]
- Lin, K.Z. Research on Control Method of Permanent Magnet Motor under Low Switching Frequency. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2014. [Google Scholar]
- Xu, M.; Wu, X.M.; Yu, X.; Chen, G.J. Dynamic performance of auxiliary hydraulic power unit based electro-hydraulic variable speed drive system. Proc. Inst. Mech. Eng. C J. Mech. Eng. 2017, 232, 1–11. [Google Scholar] [CrossRef]
- Wu, M.G.; Zhao, R.X. Analysis of torque ripples of vector-controlled permanent magnet synchronous motor. Trans. China Electrotech. Soc. 2007, 22, 9–14. [Google Scholar]
- Chen, L.H.; Han, W.N.; Lu, Y.M.; Cai, Y. Research on speed control of variable speed pump controlled motor system based on LQ. Mach. Tool Hydraul. 2017, 45, 20–22, 80. [Google Scholar]
- Meng, Z.L. Performance Analysis and Control Research of Variable Frequency Pump Controlled Motor System. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2017. [Google Scholar]
- Yuan, L.; Hu, B.X.; Wei, K.Y.; Chen, S. Control Principle and MATLAB Simulation of Modern Permanent Magnet Synchronous Motor; Beijing University of Aeronautics and Astronautics Press: Beijing, China, 2016; pp. 4–11, 82. [Google Scholar]
- Ma, C.G.; Zuo, S.G.; Sun; Meng, S. Order characteristic analysis of electromagnetic noise of permanent magnet synchronous motor considering time harmonic current. J. Vib. Shock 2014, 33, 180–113, 125. [Google Scholar]
- Song, B.X. The Kinetic Study and Parameter Optimization of Airborne Roofbolter. Master’s Thesis, Liaoning Technology University, Fuxin, China, 2012. [Google Scholar]
- Chen, J.S. Research on Integration of Drilling and Detection Along with Tunneling of Roadway Supported by Bolting. Ph.D. Thesis, Anhui University Science and Technology, Huainan, China, 2012. [Google Scholar]
- Liu, G.; Sun, Q.W.; Xiao, Y.R. Permanent magnet synchronous motor current harmonics suppression based on coordinate transformation. Elect. Mach. Control. 2015, 19, 30–36. [Google Scholar]
- Ji, S.Z. A harmonic current suppression algorithm for permanent magnet synchronous motor. Power Electron. Technol. 2019, 53, 109–110, 114. [Google Scholar]
- Li, S.; Sun, L.Z.; Liu, X.Y.; An, Q.T. Current harmonic suppression strategy of permanent magnet synchronous motor. Trans. China Electrotech. Soc. 2019, 34, 87–96. [Google Scholar]








| Symbol | Physical Significance | Value |
|---|---|---|
| Lq (mH) | q-axis inductance | 50 |
| Ld (mH) | d-axis inductance | 50 |
| R (Ω) | stator winding resistance | 1.3 |
| ψf (Wb) | motor rotor flux | 1 |
| JT (kg·m2) | moment of inertia | 0.09 |
| BT (N·m·s) | damping coefficient | 0.0008 |
| Pn | number of motor rotor pole pairs | 2 |
| td (μs) | dead time | 3 |
| ud (V) | pressure drop of pipe resistance | 1 |
| Dpg (m3/rad) | displacement of pump1 | 2.5 × 10−6 |
| Dpm (m3/rad) | displacement of pump2 | 4 × 10−5 |
| ηpm | mechanical efficiency of pump | 0.95 |
| βb(N/m2) | bulk elastic modulus of oil in a closed chamber | 9.0 × 108 |
| Dm (m3/rad) | displacement of motor | 8 × 10−5 |
| Jm (kg·m2) | equivalent moment of inertia of motor output shaft | 3 |
| d1 (mm) | diameter of rod cavity of hydraulic cylinder | 40 |
| d2 (mm) | diameter of rodless cavity of hydraulic cylinder | 20 |
| D (mm) | diameter of outside the drill | 27 |
| Bg | damping coefficient of hydraulic cylinder | 1000 |
| s (m) | stroke of hydraulic cylinders | 2 |
| kp | scale factor of PI | 250 |
| ki | integral time constant of PI | 6500 |
| c | sliding surface parameter of SMC | 2 |
| ε | the system overcomes the perturbation and external interference parameter of SMC | 171 |
| q | approaching speed parameter of SMC | 55 |
| Physical Variable | f = 5 | f = 6 | f = 7 | |||
|---|---|---|---|---|---|---|
| CSPI | CSSMC | CSPI | CSSMC | CSPI | CSSMC | |
| the pulsation coefficient of the outlet pressure of pump | 6.46% | 2.10% | 5.87% | 0.39% | 4.03% | 0.98% |
| the pulsation coefficient of the hydraulic motor speed | 1.12% | 0.69% | 1.32% | 0.18% | 4.72% | 0.97% |
| the pulsation coefficient of the hydraulic cylinder speed | 18.18% | 0.72% | 17.02% | 0.31% | 44.09% | 0.50% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, G.; Guo, Y.; Wang, P.; Cheng, G.; Zhao, D. Research on Control Method of the Power System of Stepping-Type Anchoring Equipment. Sensors 2021, 21, 7123. https://doi.org/10.3390/s21217123
Su G, Guo Y, Wang P, Cheng G, Zhao D. Research on Control Method of the Power System of Stepping-Type Anchoring Equipment. Sensors. 2021; 21(21):7123. https://doi.org/10.3390/s21217123
Chicago/Turabian StyleSu, Guoyong, Yongcun Guo, Pengyu Wang, Gang Cheng, and Dongyang Zhao. 2021. "Research on Control Method of the Power System of Stepping-Type Anchoring Equipment" Sensors 21, no. 21: 7123. https://doi.org/10.3390/s21217123






