Recent Progress of Fluxgate Magnetic Sensors: Basic Research and Application
Abstract
:1. Introduction
2. Basic Research
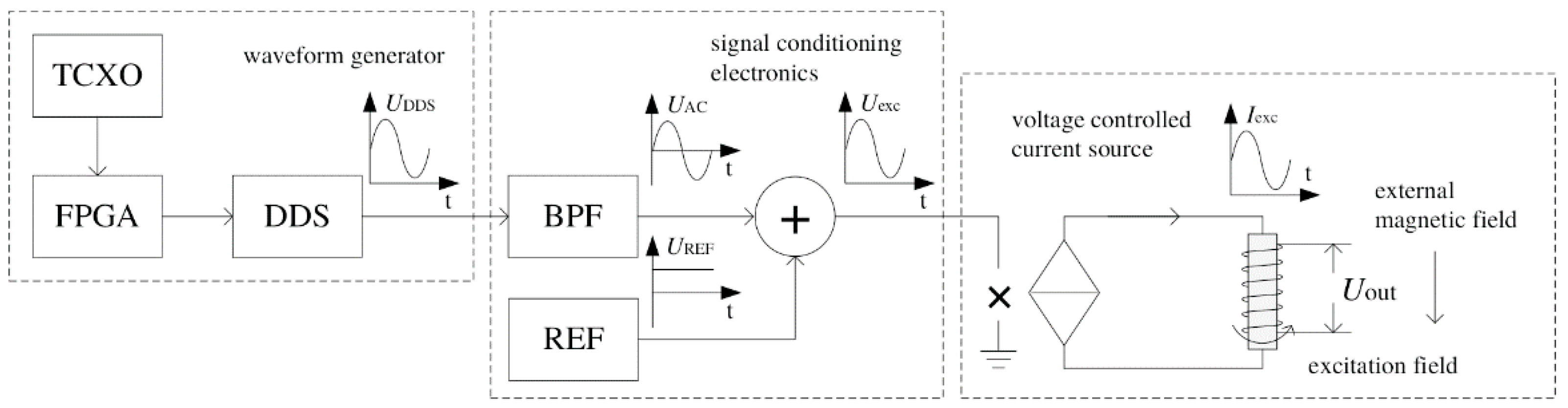
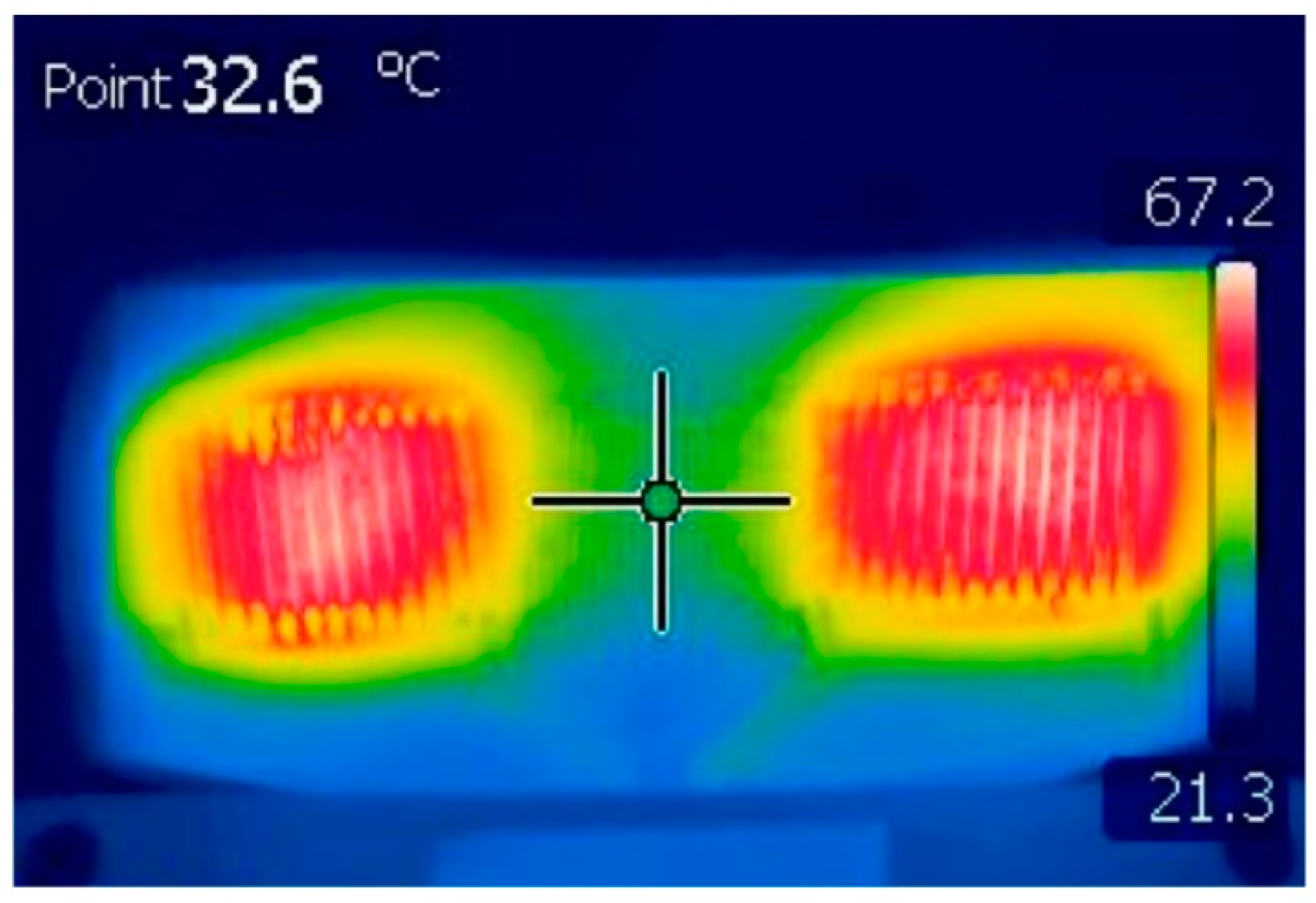
2.1. Noise
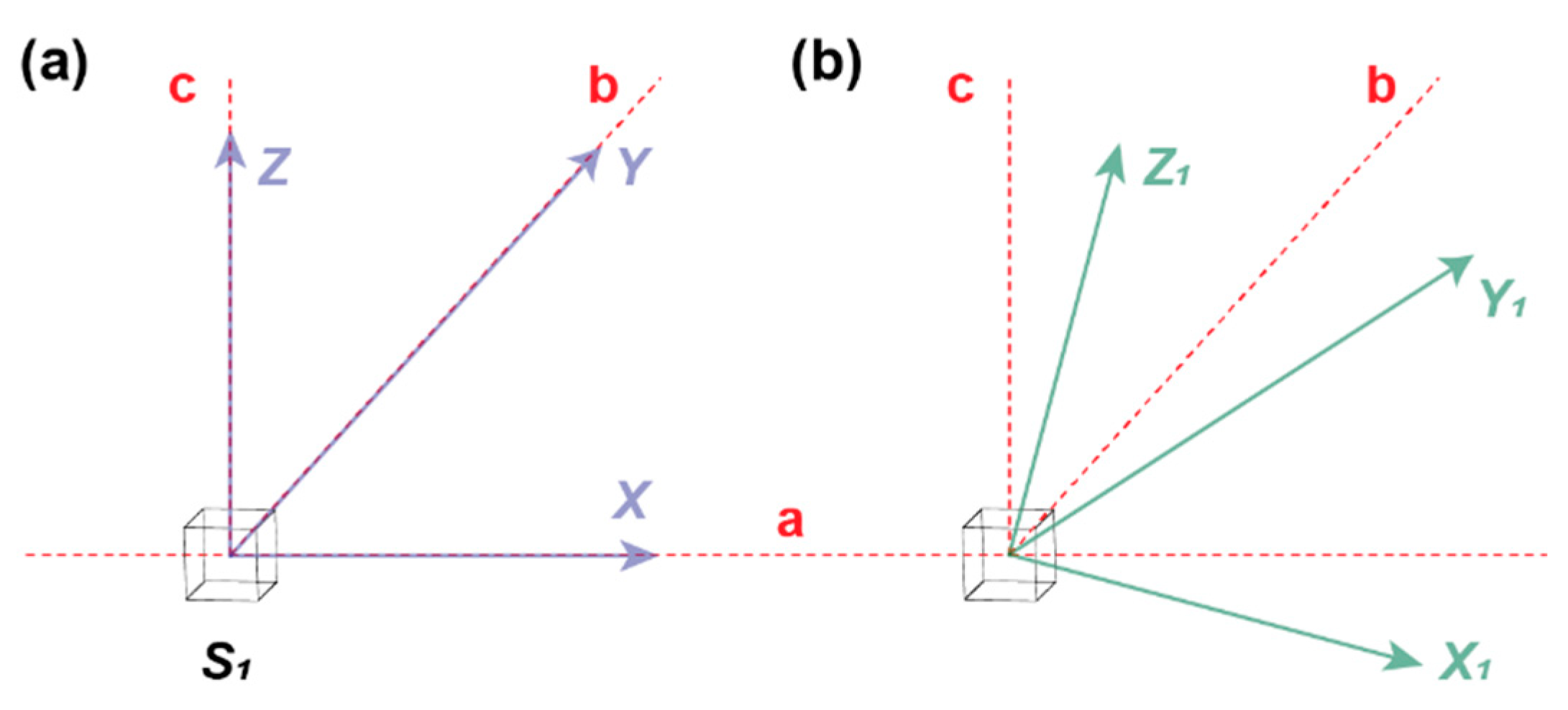
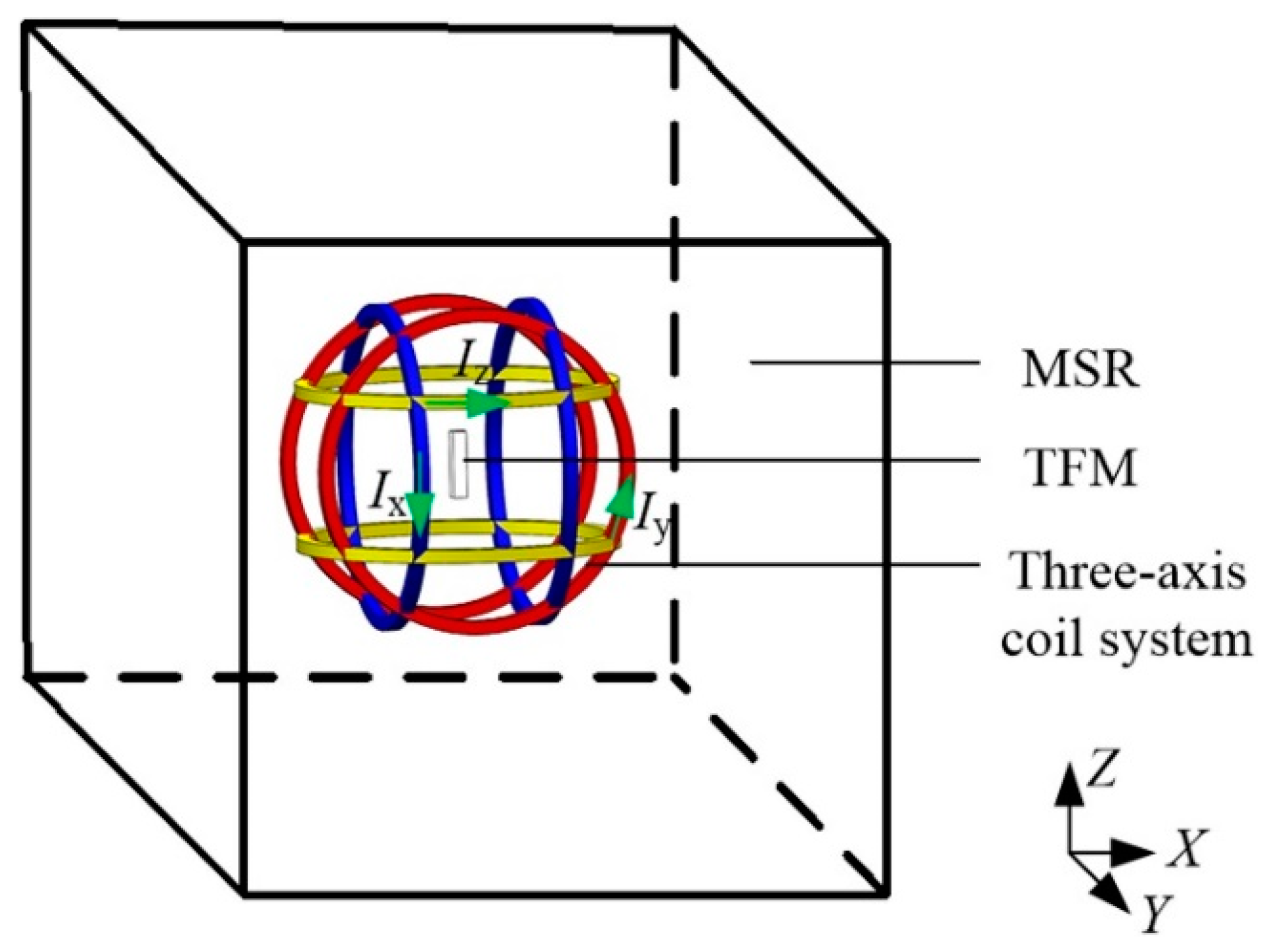
2.2. Errors and Calibration Methods
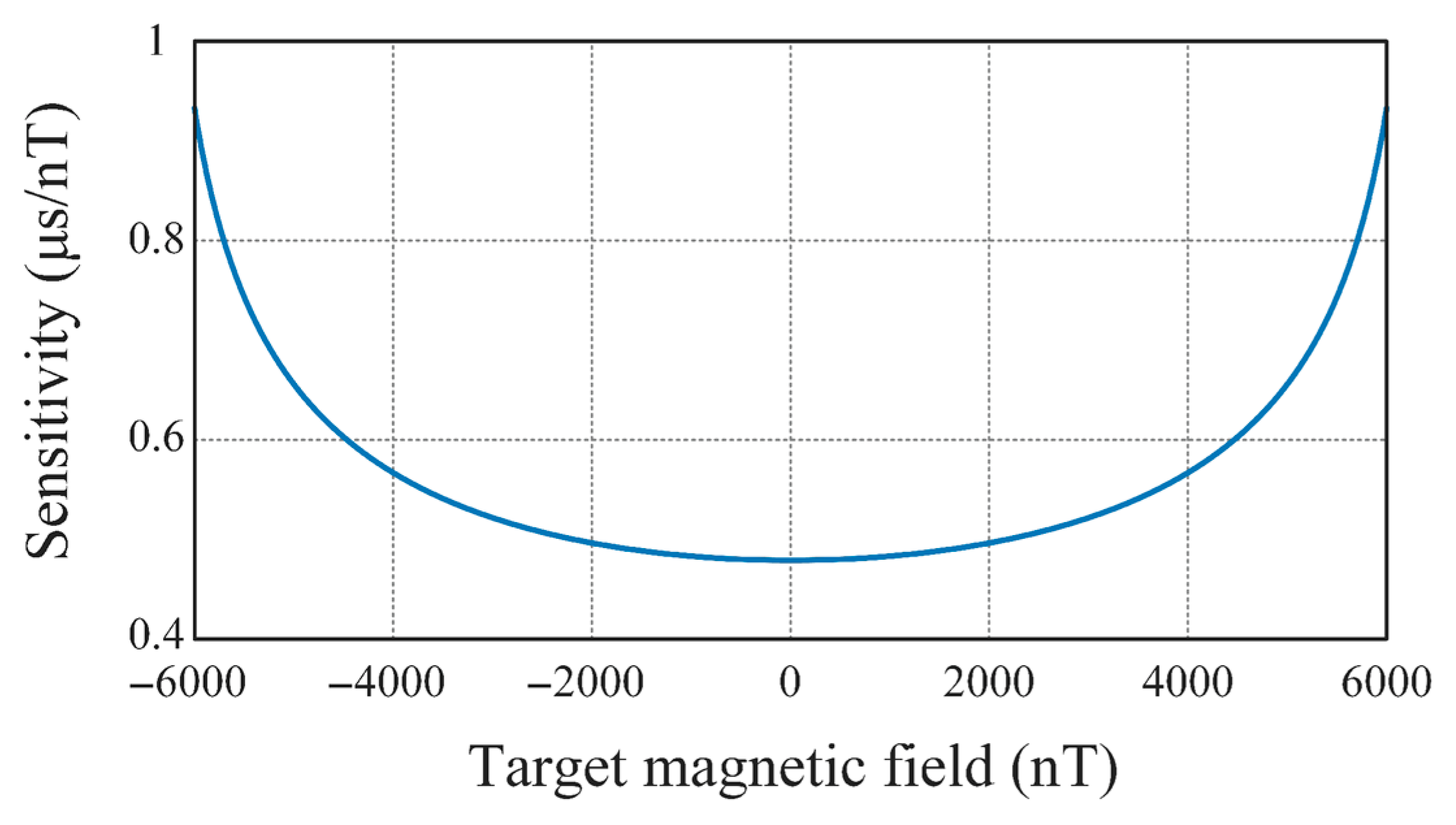
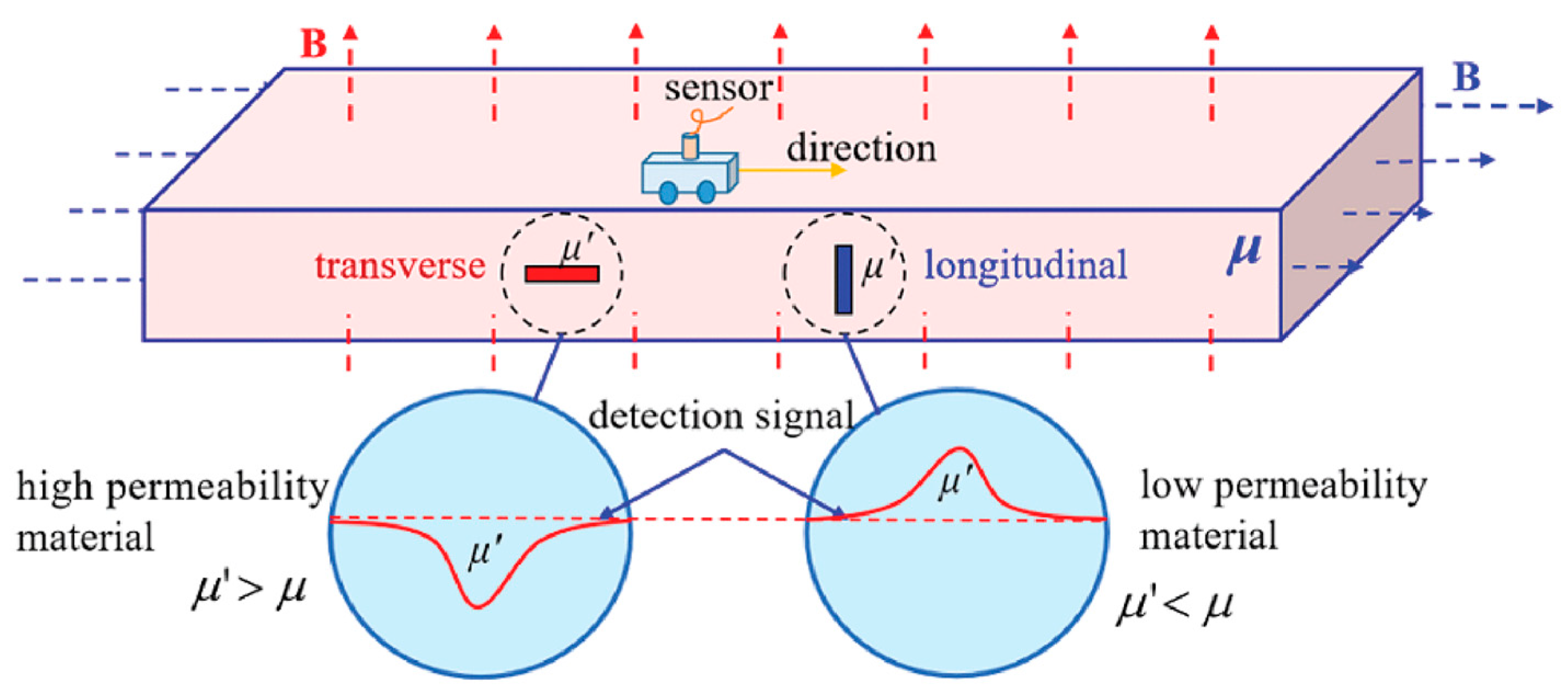
2.3. Sensitivity and Other Related Research Works
3. Applications
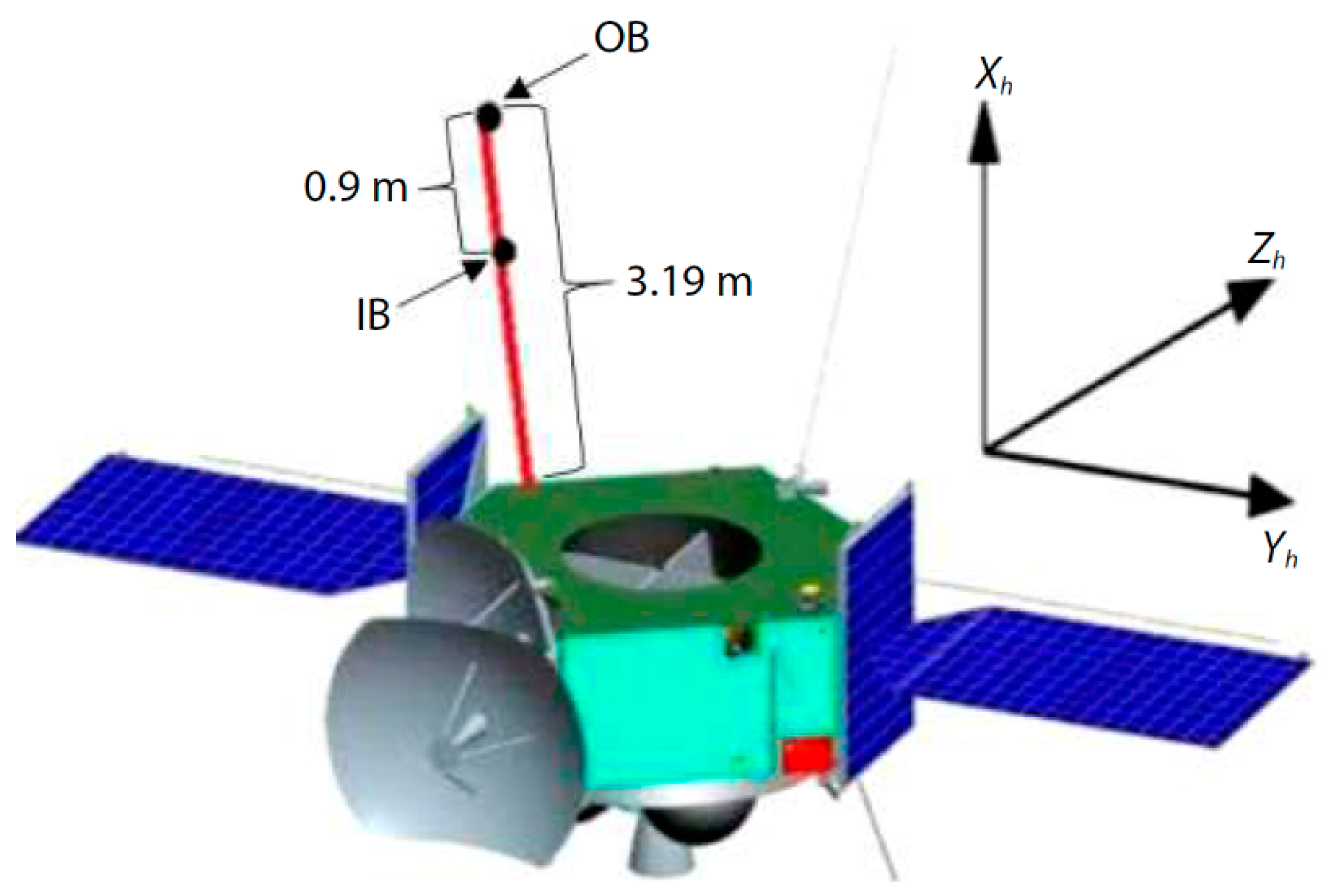
3.1. Astro Observation
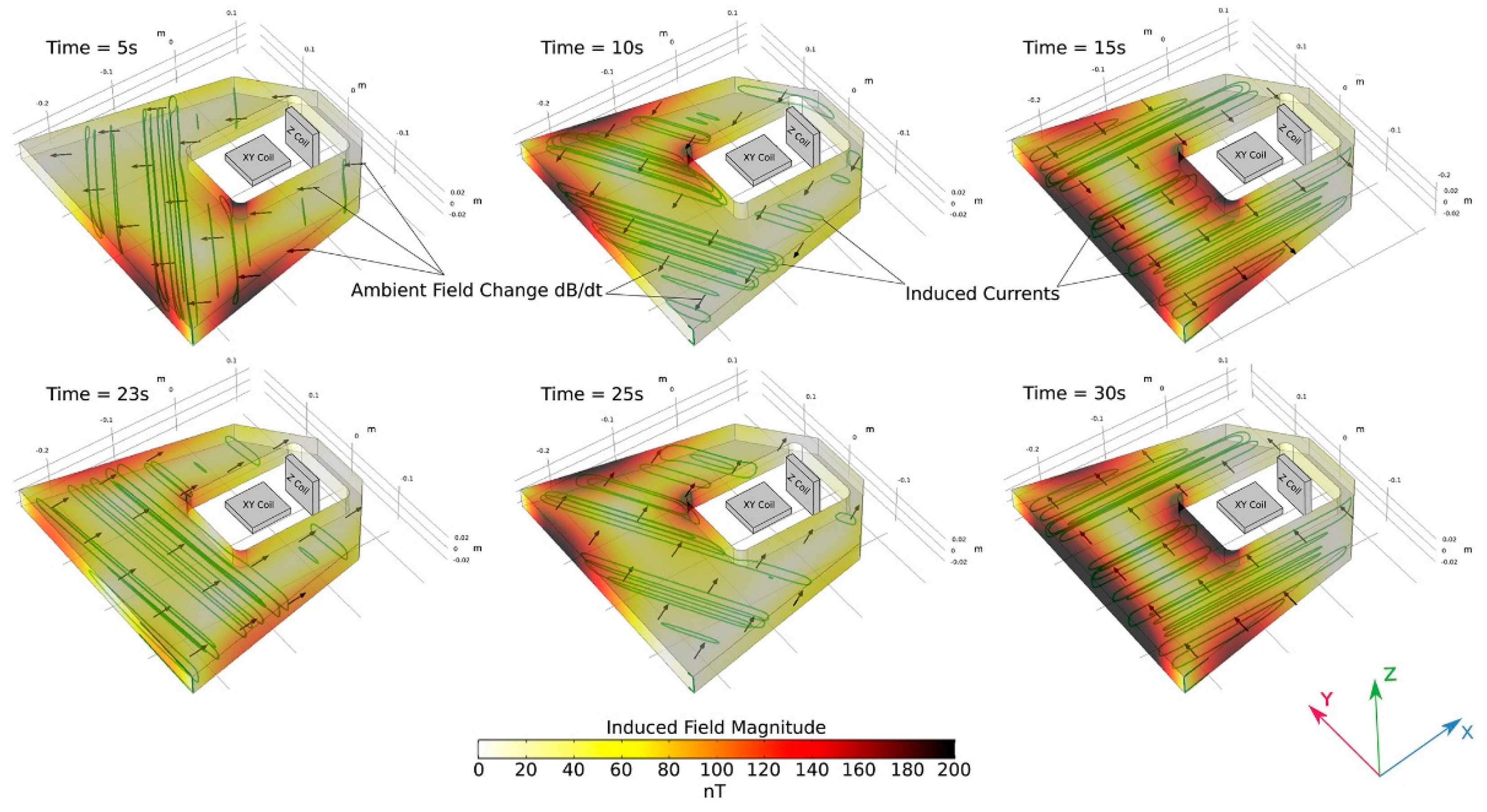
3.2. Geophysics Observation
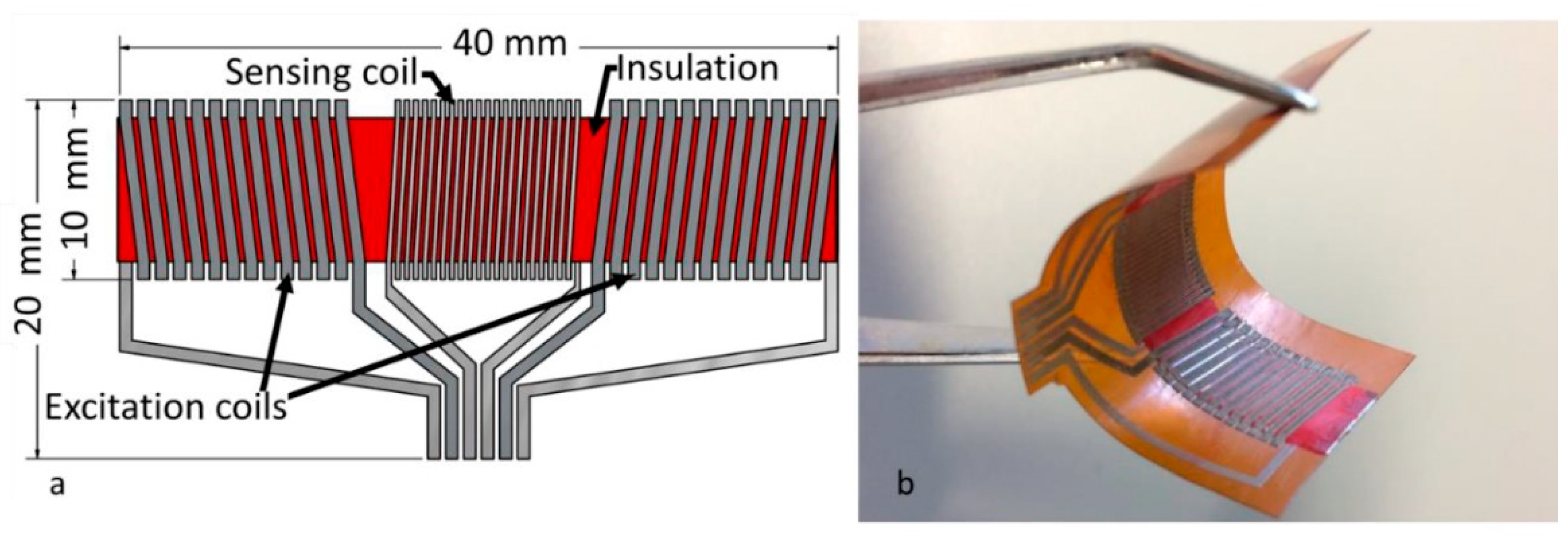
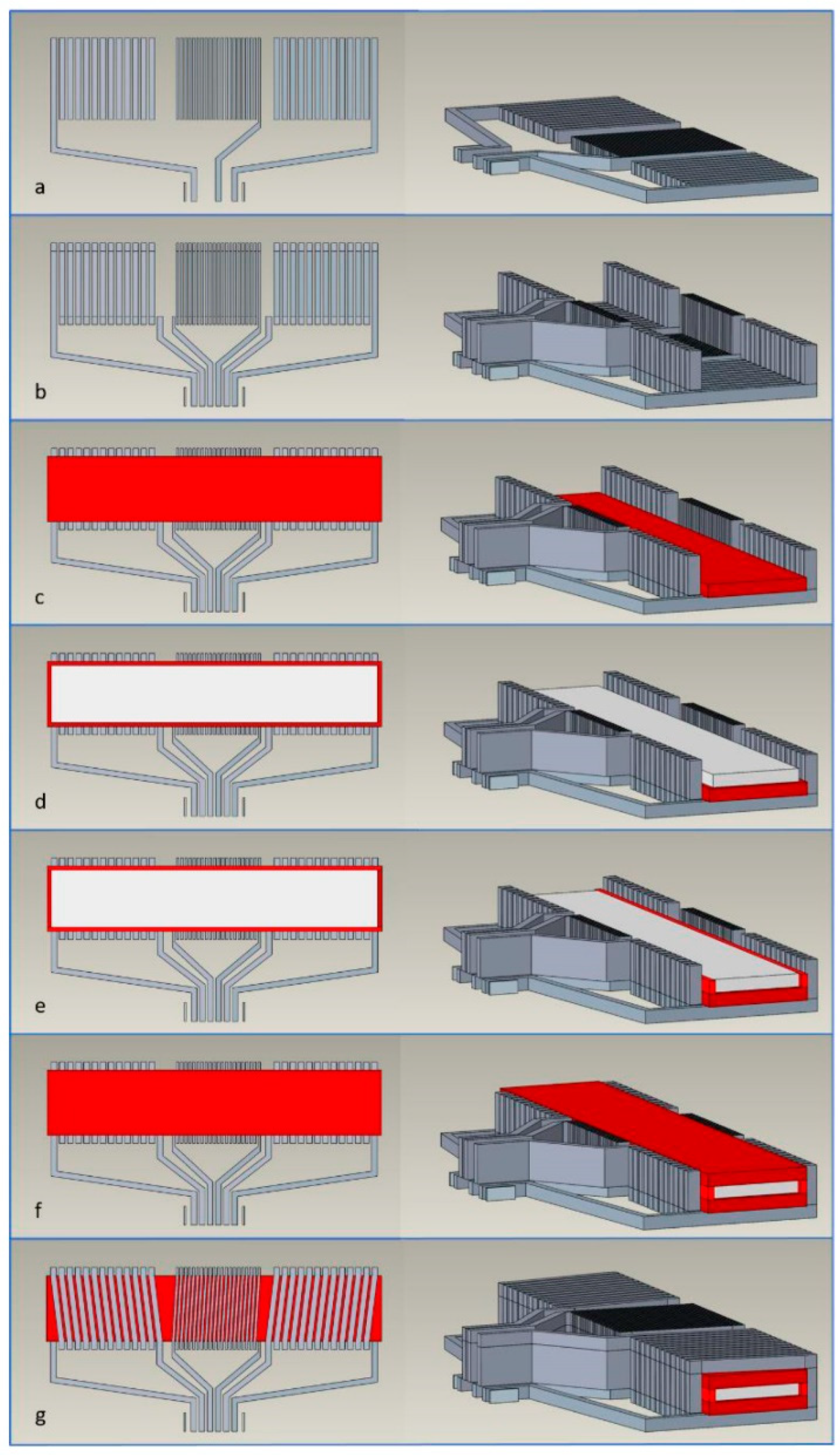
3.3. Other Related Applications
4. Summary and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dentith, M.; Mudge, S.T. Geophysics for the Mineral Exploration Geoscientist; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Sheard, S.; Ritchie, T.; Christopherson, K.R.; Brand, E. Mining, environmental, petroleum, and engineering industry applications of electromagnetic techniques in geophysics. Sur. Geophys. 2005, 26, 653–669. [Google Scholar] [CrossRef]
- Ziadi, A.; Hariga, N.T.; Tarhouni, J. Use of time-domain electromagnetic (TDEM) method to investigate seawater intrusion in the Lebna coastal aquifer of eastern Cap Bon, Tunisia. Arab. J. Geosci. 2017, 10, 492. [Google Scholar] [CrossRef]
- Nagendran, R.; Mohanty, I.; Arasu, A.T.; Baskaran, R. Transient eddy current NDE system based on fluxgate sensor for the detection of defects in multilayered conducting material. J. Nondestr. Eval. 2018, 37, 52. [Google Scholar] [CrossRef]
- Wang, H.; Chen, S.; Zhang, S.; Yuan, Z.; Zhang, H.; Fang, D.; Zhu, J. A high-performance portable transient electro-magnetic sensor for unexploded ordnance detection. Sensors 2017, 17, 2651. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, N.; Zhang, Z.; Li, Z.; Zhang, Y.; He, Q.; Han, B.; Lu, Y. Self-oscillating fluxgate-based quasi-digital sensor for DC high-current measurement. IEEE Trans. Instrum. Meas. 2015, 64, 3555–3563. [Google Scholar] [CrossRef]
- Schrittwieser, L.; Mauerer, M.; Bortis, D.; Ortiz, G.; Kolar, J.W. Novel principle for flux sensing in the application of a DC+ AC current sensor. IEEE Trans. Ind. Appl. 2015, 51, 4100–4110. [Google Scholar] [CrossRef]
- Yang, X.; Li, Y.; Zheng, W.; Guo, W.; Wang, Y.; Yan, R. Design and realization of a novel compact fluxgate current sensor. IEEE Trans. Magn. 2015, 51, 4002804. [Google Scholar] [CrossRef]
- Yang, X.; Li, Y.; Guo, W.; Zheng, W.; Xie, C.; Yu, H. A new compact fluxgate current sensor for AC and DC application. IEEE Trans. Magn. 2014, 50, 4005704. [Google Scholar] [CrossRef]
- Yang, X.; Guo, W.; Li, C.; Zhu, B.; Pang, L.; Wang, Y. A fluxgate current sensor with a U-shaped magnetic gathering shell. IEEE Trans. Magn. 2015, 51, 4005504. [Google Scholar] [CrossRef]
- Trigona, C.; Sinatra, V.; Ando, B.; Baglio, S.; Bulsara, A.R. Flexible microwire residence times difference fluxgate magnetometer. IEEE Trans. Instrum. Meas. 2017, 66, 559–568. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X.; Shi, J.; Heidari, H.; Wang, Y. Performance Degradation Effect Countermeasures in Residence Times Difference (RTD) Fluxgate Magnetic Sensors. IEEE Sens. J. 2019, 19, 11819–11827. [Google Scholar] [CrossRef] [Green Version]
- Wrzecionko, B.; Steinmann, L.; Kolar, J.W. Fast high-temperature (250 °C/500 °F) isolated dc and ac current measurement: Bidirectionally saturated current transformer. In Proceedings of the 7th International Power Electronics and Motion Control Conference, Harbin, China, 2–5 June 2012; pp. 480–487. [Google Scholar]
- Wrzecionko, B.; Steinmann, L.; Kolar, J.W. High-bandwidth high-temperature (250 °C/500 °F) isolated DC and AC current measurement: Bidirectionally saturated current transformer. IEEE Trans. Power Electron. 2013, 28, 5404–5413. [Google Scholar] [CrossRef]
- Szewczyk, R.; Ostaszewska-Liżewska, A.; Råback, P. Modelling the Fluxgate Sensors with Magnetic Field Concentrators. Acta Phys. Pol. A 2020, 137. [Google Scholar] [CrossRef]
- Chen, S.; Wang, Y.; Li, J.; Piao, H.; Lin, J. Sensitivity Model for Residence Times Difference Fluxgate Magnetometers Near Zero Magnetic Field. IEEE Sens. J. 2019, 20, 868–875. [Google Scholar] [CrossRef]
- Lee, T.-M.; Hur, S.; Kim, J.-H.; Choi, H.-C. EL device pad-printed on a curved surface. J. Micromech. Microeng. 2009, 20, 015016. [Google Scholar] [CrossRef]
- Krebs, F.C. Pad printing as a film forming technique for polymer solar cells. Sol. Energy Mater. Sol. Cells 2009, 93, 484–490. [Google Scholar] [CrossRef]
- Mooring, L.; Karousos, N.G.; Livingstone, C.; Davis, J.; Wildgoose, G.G.; Wilkins, S.J.; Compton, R.G. Evaluation of a novel pad printing technique for the fabrication of disposable electrode assemblies. Sens. Actuators B 2005, 107, 491–496. [Google Scholar] [CrossRef]
- Butta, M.; Vazquez, M.; Perez del Real, R.; Calle, E. Dependence of the noise of an orthogonal fluxgate on the composition of its amorphous wire-core. AIP Adv. 2020, 10, 025114. [Google Scholar] [CrossRef]
- Butta, M.; Sasada, I. Sources of noise in a magnetometer based on orthogonal fluxgate operated in fundamental mode. IEEE Trans. Magn. 2012, 48, 1508–1511. [Google Scholar] [CrossRef]
- Butta, M.; Sasada, I. Method for offset suppression in orthogonal fluxgate with annealed wire core. Sens. Lett. 2014, 12, 1295–1298. [Google Scholar] [CrossRef]
- Butta, M.; Janosek, M.; Schutte, B.P.; Vazquez, M.; Perez, R.; Ramirez, E.C.; Jimenez, A. Effect of amorphous wire core diameter on the noise of an orthogonal fluxgate. IEEE Trans. Magn. 2018, 54, 2002805. [Google Scholar] [CrossRef]
- Song, S.; Deng, M.; Chen, K.; Yuan, Z.; Xu, Z.; Zhang, Q. Excitation module for orthogonal fundamental mode fluxgate sensor. J. Instrum. 2020, 15, P05007. [Google Scholar] [CrossRef]
- Janosek, M.; Butta, M.; Dressler, M.; Saunderson, E.; Novotny, D.; Fourie, C. 1-pT noise fluxgate magnetometer for geomagnetic measurements and unshielded magnetocardiography. IEEE Trans. Instrum. Meas. 2019, 69, 2552–2560. [Google Scholar] [CrossRef]
- Pedersen, L.W.; Merenyi, L. The FGE magnetometer and the INTERMAGNET 1 second standard. J. Ind. Geophys. Union 2016, 2, 30–36. [Google Scholar]
- Včelák, J.; Ripka, P.; Zikmund, A. Precise magnetic sensors for navigation and prospection. J. Supercond. Novel Magn. 2015, 28, 1077–1080. [Google Scholar] [CrossRef]
- Forslund, Å.; Belyayev, S.; Ivchenko, N.; Olsson, G.; Edberg, T.; Marusenkov, A. Miniaturized digital fluxgate magnetometer for small spacecraft applications. Meas. Sci. Technol. 2007, 19, 015202. [Google Scholar] [CrossRef]
- Chave, A.D.; Jones, A.G. The Magnetotelluric Method: Theory and Practice; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Bazinet, R.; Jacas, A.; Confalonieri, G.A.B.; Vazquez, M. A low-noise fundamental-mode orthogonal fluxgate magnetometer. IEEE Trans. Magn. 2013, 50, 1–3. [Google Scholar] [CrossRef] [Green Version]
- Mohanty, I.; Nagendran, R.; Arasu, A.T.; Baskaran, R.; Mani, A. Correlation of defect depth with diffusion time of eddy currents for the defects in conducting materials using transient eddy current NDE. Meas. Sci. Technol. 2018, 29, 105601. [Google Scholar] [CrossRef]
- Ficko, B.W.; Nadar, P.M.; Hoopes, P.J.; Diamond, S.G. Development of a magnetic nanoparticle susceptibility magnitude imaging array. Phys. Med. Biol. 2014, 59, 1047. [Google Scholar] [CrossRef] [Green Version]
- Harada, S.; Sasada, I.; Hang, F. Development of a One-Dimensional Fluxgate Array and Its Application to Magnetocardiogram Measurements. Electron. Commun. Jpn. 2015, 98, 20–26. [Google Scholar] [CrossRef]
- Dolabdjian, C.; Saez, S.; Reyes Toledo, A.; Robbes, D. Signal-to-noise improvement of bio-magnetic signals using a flux-gate probe and real time signal processing. Rev. Sci. Instrum. 1998, 69, 3678–3680. [Google Scholar] [CrossRef]
- Hinnrichs, C.; Stahl, J.; Kuchenbrandt, K.; Schilling, M. Dependence of sensitivity and noise of fluxgate sensors on racetrack geometry. IEEE Trans. Magn. 2001, 37, 1983–1985. [Google Scholar] [CrossRef]
- Janošek, M.; Vyhnánek, J.; Zikmund, A.; Butvin, P.; Butvinová, B. Effects of core dimensions and manufacturing procedure on fluxgate noise. Acta Phys. Pol. A 2014. [Google Scholar] [CrossRef]
- Korepanov, V.; Marusenkov, A. Flux-gate magnetometers design peculiarities. Sur. Geophys. 2012, 33, 1059–1079. [Google Scholar] [CrossRef] [Green Version]
- Koch, R.; Rozen, J. Low-noise flux-gate magnetic-field sensors using ring-and rod-core geometries. Appl. Phys. Lett. 2001, 78, 1897–1899. [Google Scholar] [CrossRef]
- Marusenkov, A. Possibilities of further improvement of 1 s fluxgate variometers. Geosci. Instrum. Methods Data Syst. 2017, 6, 301. [Google Scholar] [CrossRef] [Green Version]
- Sasada, I. Orthogonal fluxgate mechanism operated with dc biased excitation. J. Appl. Phys. 2002, 91, 7789–7791. [Google Scholar] [CrossRef]
- Xu, C.; Huang, K.; Zhang, S.; Meng, L. Study on the calibration method for tri-axis fluxgate gradiometer. IOP Conf. Ser. Earth Environ. Sci. 2020, 446, 052087. [Google Scholar] [CrossRef]
- Pan, D.; Li, J.; Jin, C.; Liu, T.; Lin, S.; Li, L. A New Calibration Method for Triaxial Fluxgate Magnetometer Based on Magnetic Shielding Room. IEEE Trans. Ind. Electron. 2019, 67, 4183–4192. [Google Scholar] [CrossRef]
- Lassahn, M.; Trenkler, G. Vectorial calibration of 3D magnetic field sensor arrays. IEEE Trans. Instrum. Meas. 1995, 44, 360–362. [Google Scholar] [CrossRef]
- Zhu, X.; Zhao, T.; Cheng, D.; Zhou, Z. A three-step calibration method for tri-axial field sensors in a 3D magnetic digital compass. Meas. Sci. Technol. 2017, 28, 055106. [Google Scholar] [CrossRef]
- Kügler, H. Simulation of DC magnetic environment on ground. In Proceedings of the Fourth International Symposium Environmental Testing for Space Programmes, Palais de Congrès, Liège, Belgium, 12–14 June 2001; p. 263. [Google Scholar]
- Zikmund, A.; Janosek, M.; Ulvr, M.; Kupec, J. Precise calibration method for triaxial magnetometers not requiring earth’s field compensation. IEEE Trans. Instrum. Meas. 2015, 64, 1242–1247. [Google Scholar] [CrossRef]
- Petrucha, V.; Kaspar, P. Calibration of a triaxial fluxgate magnetometer and accelerometer with an automated non-magnetic calibration system. In Proceedings of the SENSORS, 2009 IEEE, Christchurch, New Zealand, 25–28 October 2009; pp. 1510–1513. [Google Scholar]
- Pang, H.; Pan, M.; Wan, C.; Chen, J.; Zhu, X.; Luo, F. Integrated compensation of magnetometer array magnetic distortion field and improvement of magnetic object localization. IEEE Trans. Geosci. Electron. 2013, 52, 5670–5676. [Google Scholar] [CrossRef]
- Kubik, J.; Ripka, P. Racetrack fluxgate sensor core demagnetization factor. Sens. Actuators A 2008, 143, 237–244. [Google Scholar] [CrossRef]
- Rybalko, R.; Haueisen, J.; Hofmann, C. New type of fluxgate magnetometer for the heart’s magnetic fields detection. Curr. Direct. Biomed. Eng. 2015, 1, 22–25. [Google Scholar] [CrossRef]
- Valadeiro, J.; Cardoso, S.; Macedo, R.; Guedes, A.; Gaspar, J.; Freitas, P.P. Hybrid integration of magnetoresistive sensors with MEMS as a strategy to detect ultra-low magnetic fields. Micromachines 2016, 7, 88. [Google Scholar] [CrossRef] [Green Version]
- Baglio, S.; Bulsara, A.R.; Andò, B.; La Malfa, S.; Marletta, V.; Trigona, C.; Longhini, P.; Kho, A.; In, V.; Neff, J.D. Exploiting nonlinear dynamics in novel measurement strategies and devices: From theory to experiments and applications. IEEE Trans. Instrum. Meas. 2011, 60, 667–695. [Google Scholar] [CrossRef]
- Andò, B.; Ascia, A.; Baglio, S.; Bulsara, A.; Neff, J.; In, V. Towards an optimal readout of a residence times difference (RTD) fluxgate magnetometer. Sens. Actuators A 2008, 142, 73–79. [Google Scholar] [CrossRef]
- Yang, X.; Wen, J.; Chen, M.; Gao, Z.; Xi, L.; Li, Y. Analysis and design of a self-oscillating bidirectionally saturated fluxgate current sensor. Measurement 2020, 107687. [Google Scholar] [CrossRef]
- Ramasamy, N.; Mohanty, I. Characterization of TDEM System with SQUID and Fluxgate Magnetometers for Geophysical Applications. IEEE Trans. Appl. Supercond. 2019, 30, 1–8. [Google Scholar] [CrossRef]
- Liu, K.; Hao, X.; Li, Y.; Zhang, T.; Pan, Z.; Chen, M.; Hu, X.; Li, X.; Shen, C.; Wang, Y. Mars Orbiter magnetometer of China’s First Mars Mission Tianwen-1. Earth Planet. Phys. 2020, 4, 384–389. [Google Scholar] [CrossRef]
- Kotsiaros, S.; Connerney, J.E.; Martos, Y. Analysis of Eddy current generation on the Juno spacecraft in Jupiter’s magnetosphere. Earth Space Sci. 2020, 7, e2019EA001061. [Google Scholar] [CrossRef] [Green Version]
- Le Maire, P.; Bertrand, L.; Munschy, M.; Diraison, M.; Géraud, Y. Aerial magnetic mapping with an unmanned aerial vehicle and a fluxgate magnetometer: A new method for rapid mapping and upscaling from the field to regional scale. Geophys. Prospect. 2020, 68, 2307–2319. [Google Scholar] [CrossRef]
- Schoinas, S.; El Guamra, A.-M.; Moreillon, F.; Passeraub, P. Fabrication and Characterization of a Flexible Fluxgate Sensor with Pad-Printed Solenoid Coils. Sensors 2020, 20, 2275. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krebs, F.C. Fabrication and processing of polymer solar cells: A review of printing and coating techniques. Sol. Energy Mater. Sol. Cells 2009, 93, 394–412. [Google Scholar] [CrossRef]
- Huang, Q.; Zhu, Y. Printing conductive nanomaterials for flexible and stretchable electronics: A review of materials, processes, and applications. Adv. Mater. Technol. 2019, 4, 1800546. [Google Scholar] [CrossRef]
- Tan, H.; Tran, T.; Chua, C. A review of printed passive electronic components through fully additive manufacturing methods. Virtual Phys. Prototyp. 2016, 11, 271–288. [Google Scholar] [CrossRef]
- Khan, S.; Lorenzelli, L.; Dahiya, R.S. Technologies for printing sensors and electronics over large flexible substrates: A review. IEEE Sens. J. 2014, 15, 3164–3185. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, J.; Wang, C.; Wan, F.; He, S.; Yu, R. Non-Magnetization Detection of Arbitrary Direction Defects in Coiled Tubing Based on Fluxgate Sensor. IEEE Sens. J. 2020. [Google Scholar] [CrossRef]
- Afzal, M.; Udpa, S. Advanced signal processing of magnetic flux leakage data obtained from seamless gas pipeline. NDT&E Int. 2002, 35, 449–457. [Google Scholar] [CrossRef]
- Wang, Z.; Gu, Y.; Wang, Y. A review of three magnetic NDT technologies. J. Magn. Magn. Mater. 2012, 324, 382–388. [Google Scholar] [CrossRef]
- Liu, B.; He, L.-y.; Zhang, H.; Cao, Y.; Fernandes, H. The axial crack testing model for long distance oil-gas pipeline based on magnetic flux leakage internal inspection method. Measurement 2017, 103, 275–282. [Google Scholar] [CrossRef] [Green Version]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, S.; Liao, X.; Zhang, H.; Pang, J.; Zhou, Y. Recent Progress of Fluxgate Magnetic Sensors: Basic Research and Application. Sensors 2021, 21, 1500. https://doi.org/10.3390/s21041500
Wei S, Liao X, Zhang H, Pang J, Zhou Y. Recent Progress of Fluxgate Magnetic Sensors: Basic Research and Application. Sensors. 2021; 21(4):1500. https://doi.org/10.3390/s21041500
Chicago/Turabian StyleWei, Songrui, Xiaoqi Liao, Han Zhang, Jianhua Pang, and Yan Zhou. 2021. "Recent Progress of Fluxgate Magnetic Sensors: Basic Research and Application" Sensors 21, no. 4: 1500. https://doi.org/10.3390/s21041500





