Towards a Highly Sensitive Piezoelectric Nano-Mass Detection—A Model-Based Concept Study
Abstract
:1. Introduction
| Material | Beam Support | Resolution [g] | ω0 [MHz] | Co-Resonant | Excitation | Measurement Principle | |
|---|---|---|---|---|---|---|---|
| [9] | Silicon | single-sided | 5.5 × 10−15 | 1...10 | - | photothermal | interferometer |
| [10] | Silicon | double-sided | n.a. | 1000 | - | capacitive | capacitive |
| [11] | SiC | double-sided | 2.53 × 10−18 | 32.8 | - | capacitive | capacitive |
| [12] | CNT | single-sided | 1.3 × 10−22 | 328.5 | - | capacitive | capacitive |
| [13] | CNT | double-sided | 2.5 × 10−20 | 125 | - | capacitive | reflection |
| [14] | SiC | double-sided | n.a. | 428 | - | capacitive | capacitive |
| [5] | CNT | double-sided | 1.7 × 10−24 | 2000 | - | capacitive | reflection |
| [6] | CNT | single-sided | 1.7 × 10−24 | 12 × 104 | - | capacitive | reflection |
| [15] | Graphene | double-sided | 1.41 × 10−21 | 1.1 | + | piezoelectric | piezoresistive |
| [16] | Silicon | double-sided | 1.7 × 10−21 | 20...120 | + | capacitive | piezoresistive |
| [17] | Nano-crystalline | single-sided | 10−18 | 12 × 103 | + | capacitive | reflection |
| [18] | Silicon | single-sided | 10−12 | 1.1 | + | piezoelectric | piezoelectric |
2. Materials and Methods
2.1. Sensitivity of Relevant Mode Shapes
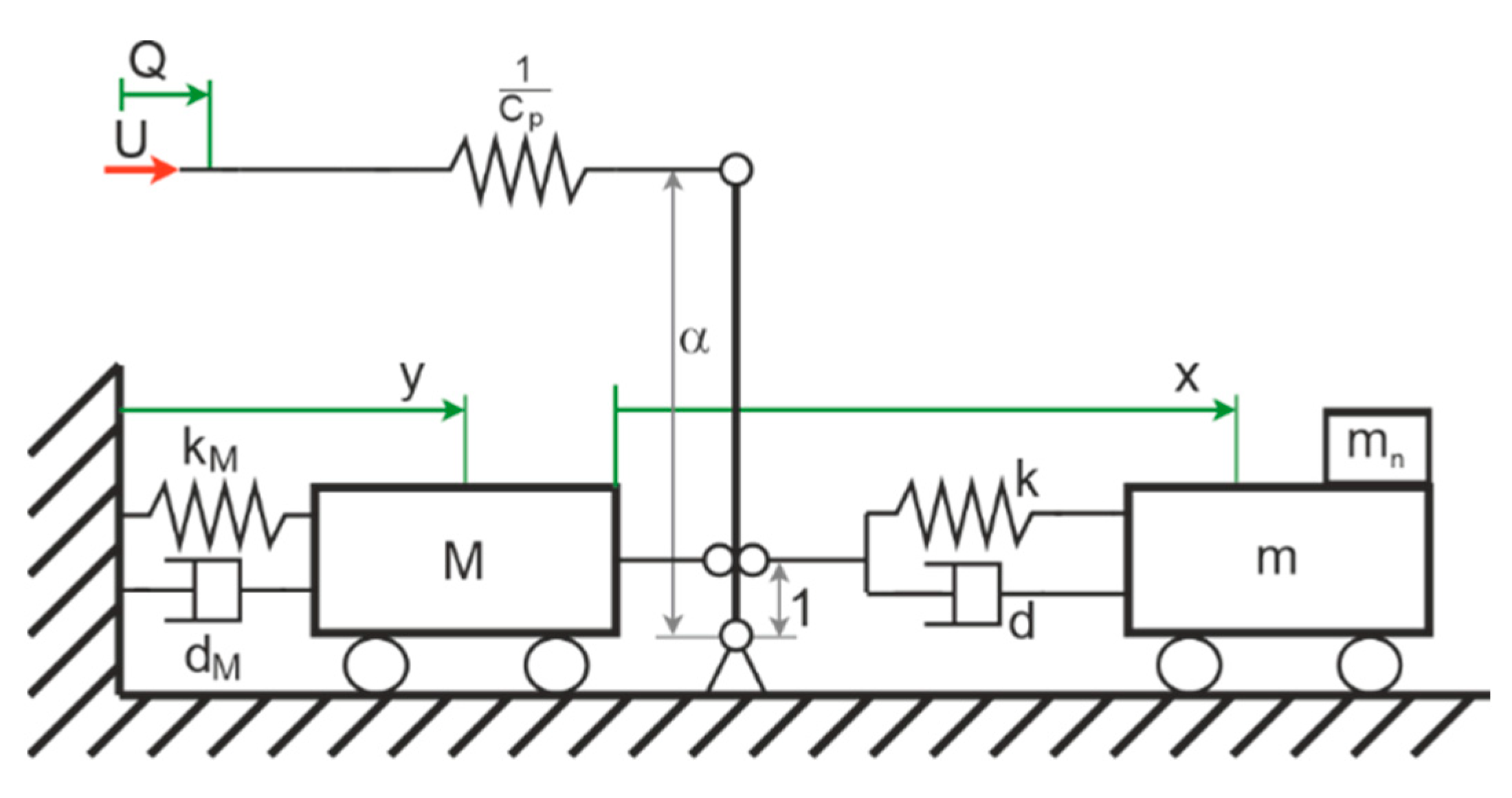
2.2. Equivalent Model for A Piezoelectric Co-Resonant Vibration System
2.3. Finite Element Simulation
3. Results and Discussion
3.1. Evaluation of Equivalent Model
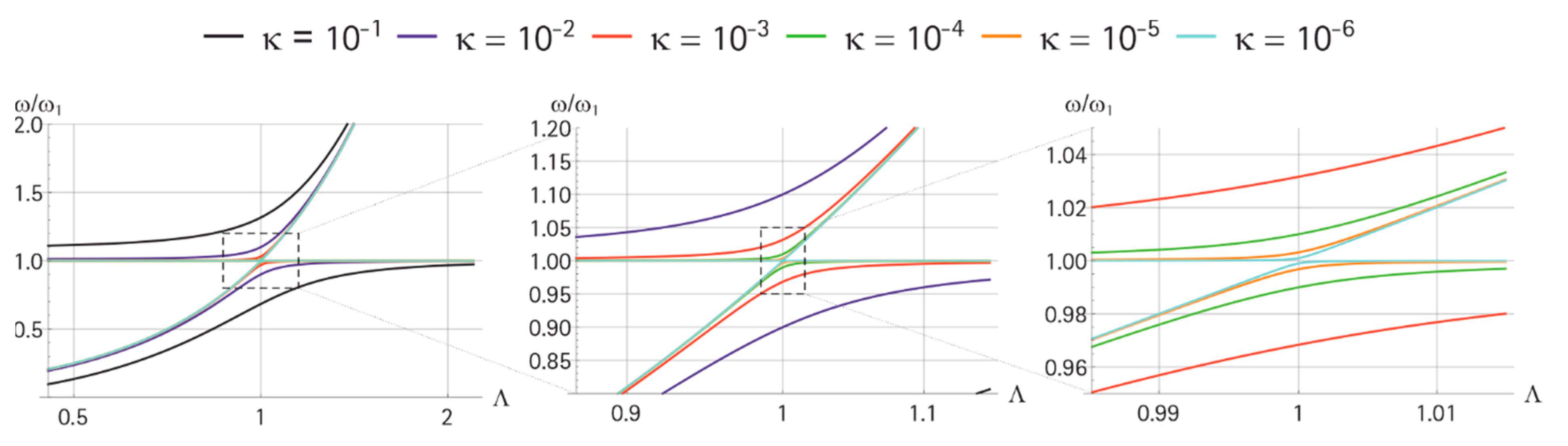
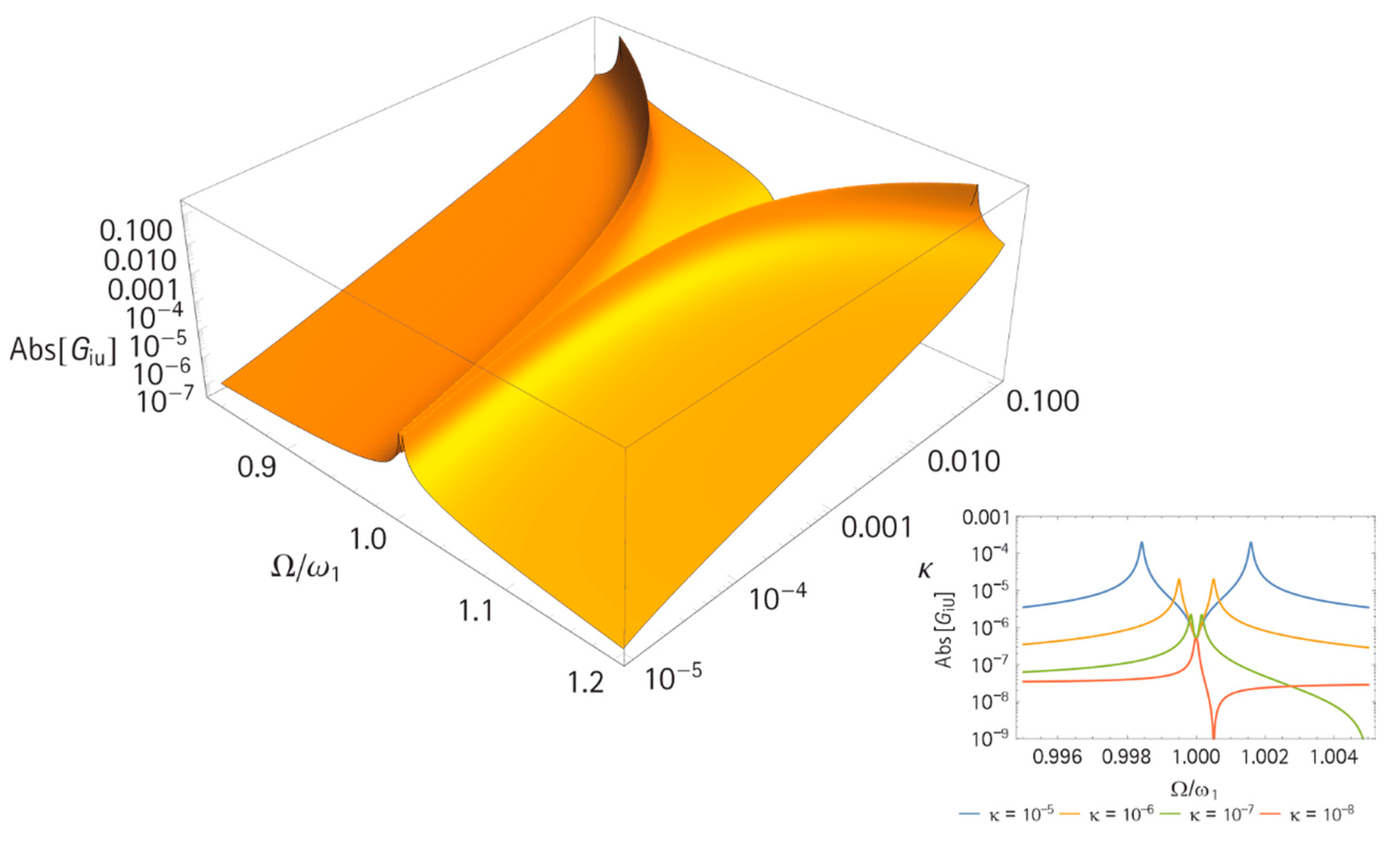
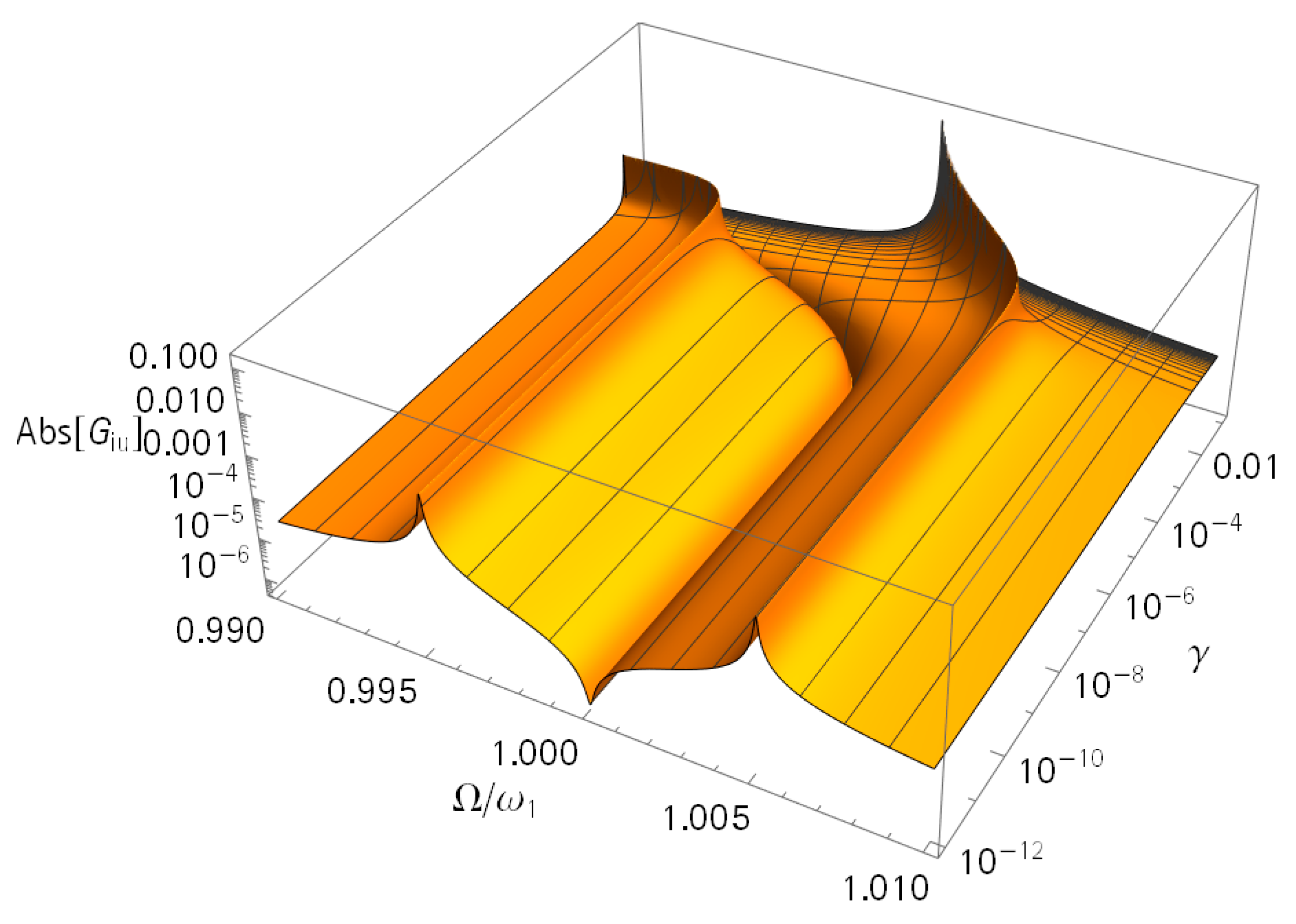
3.1.1. Coupling of the Co-Resonant Masses
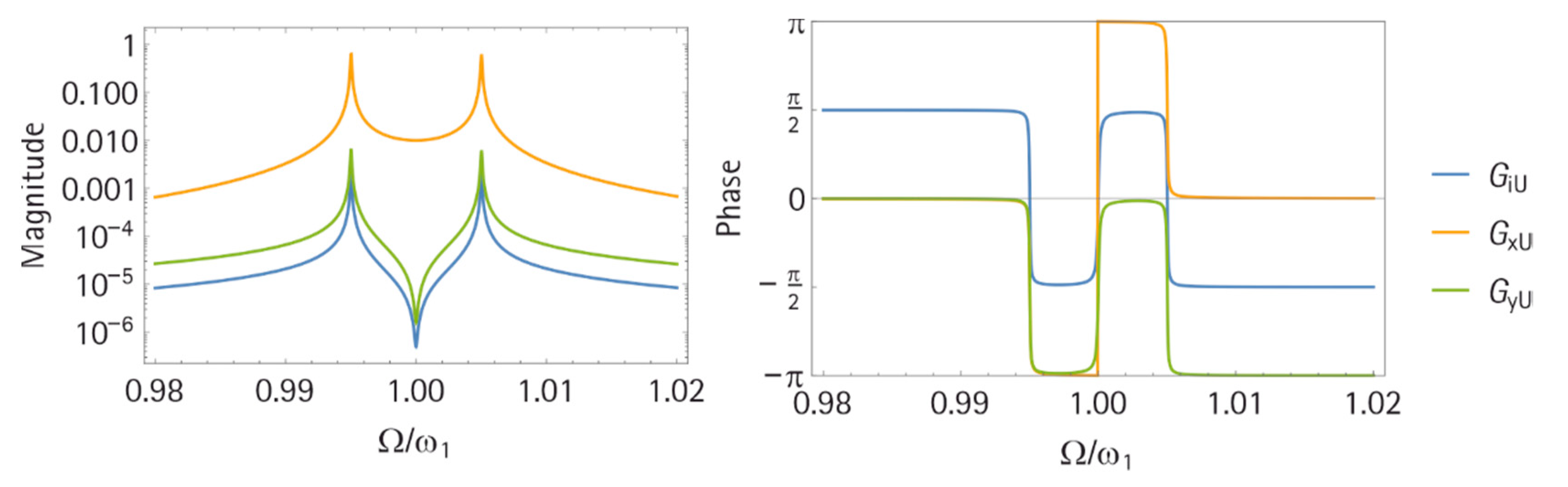
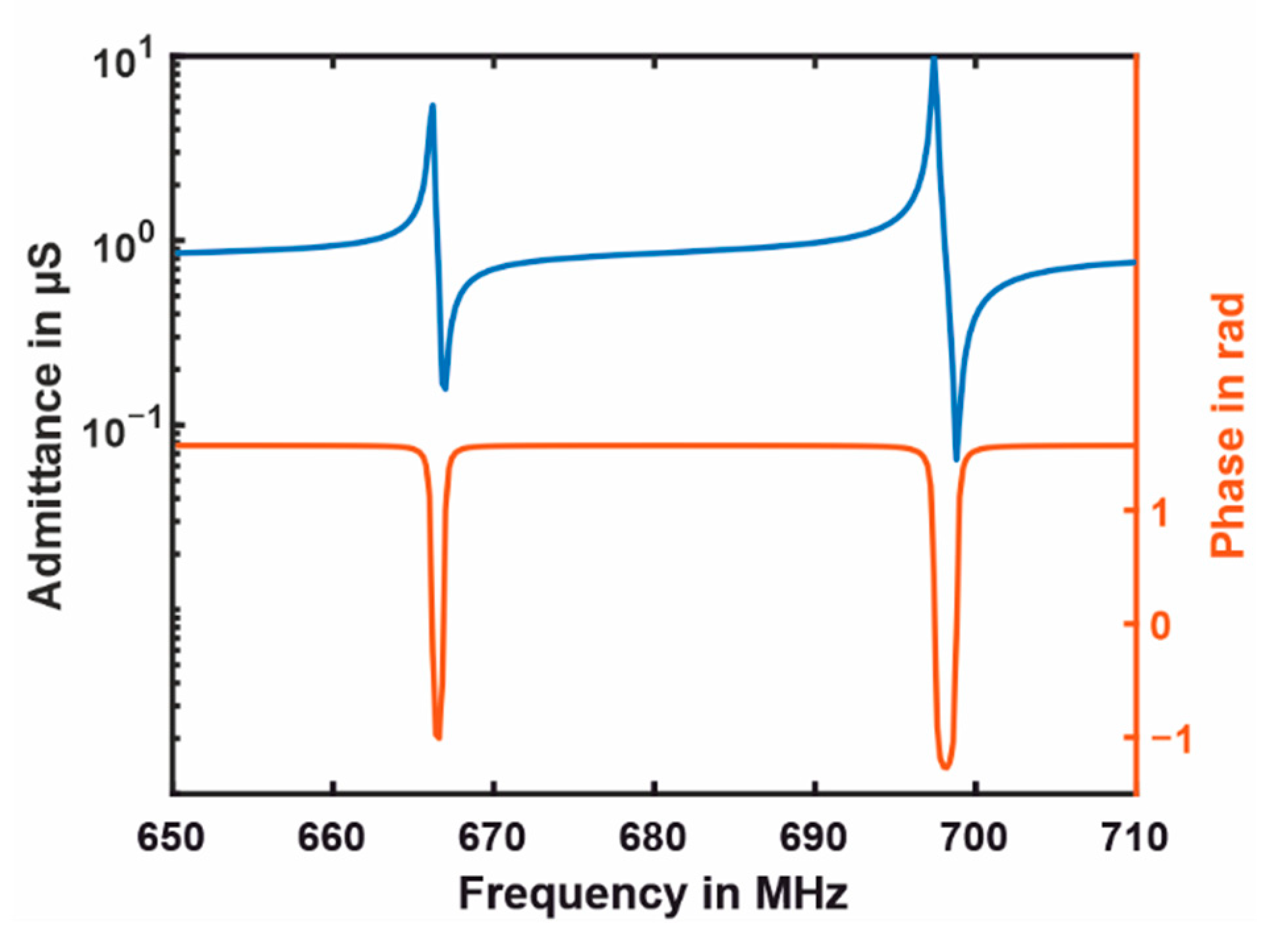
3.1.2. Frequency Response
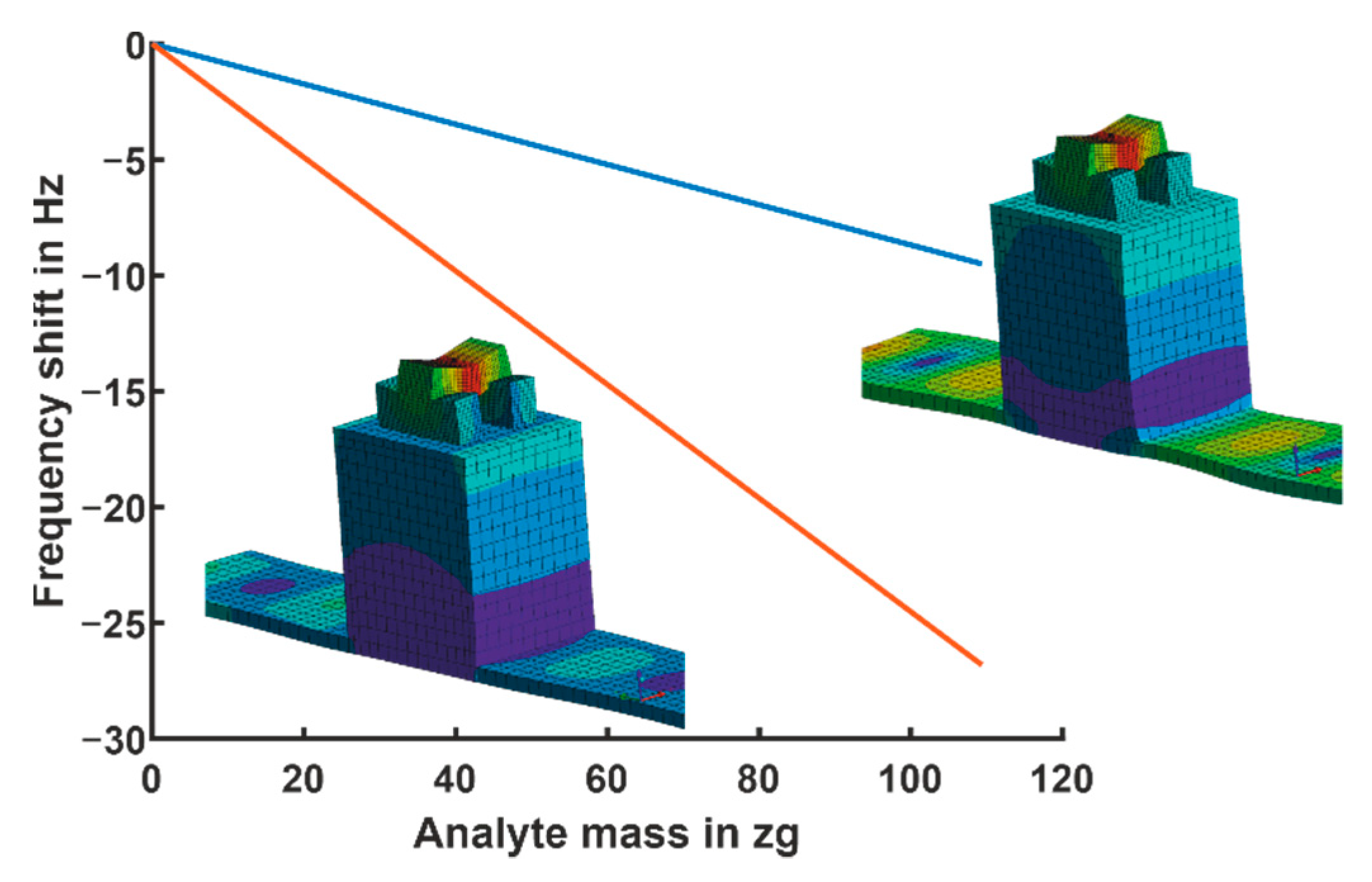
3.1.3. Sensitivity on Analyte Mass
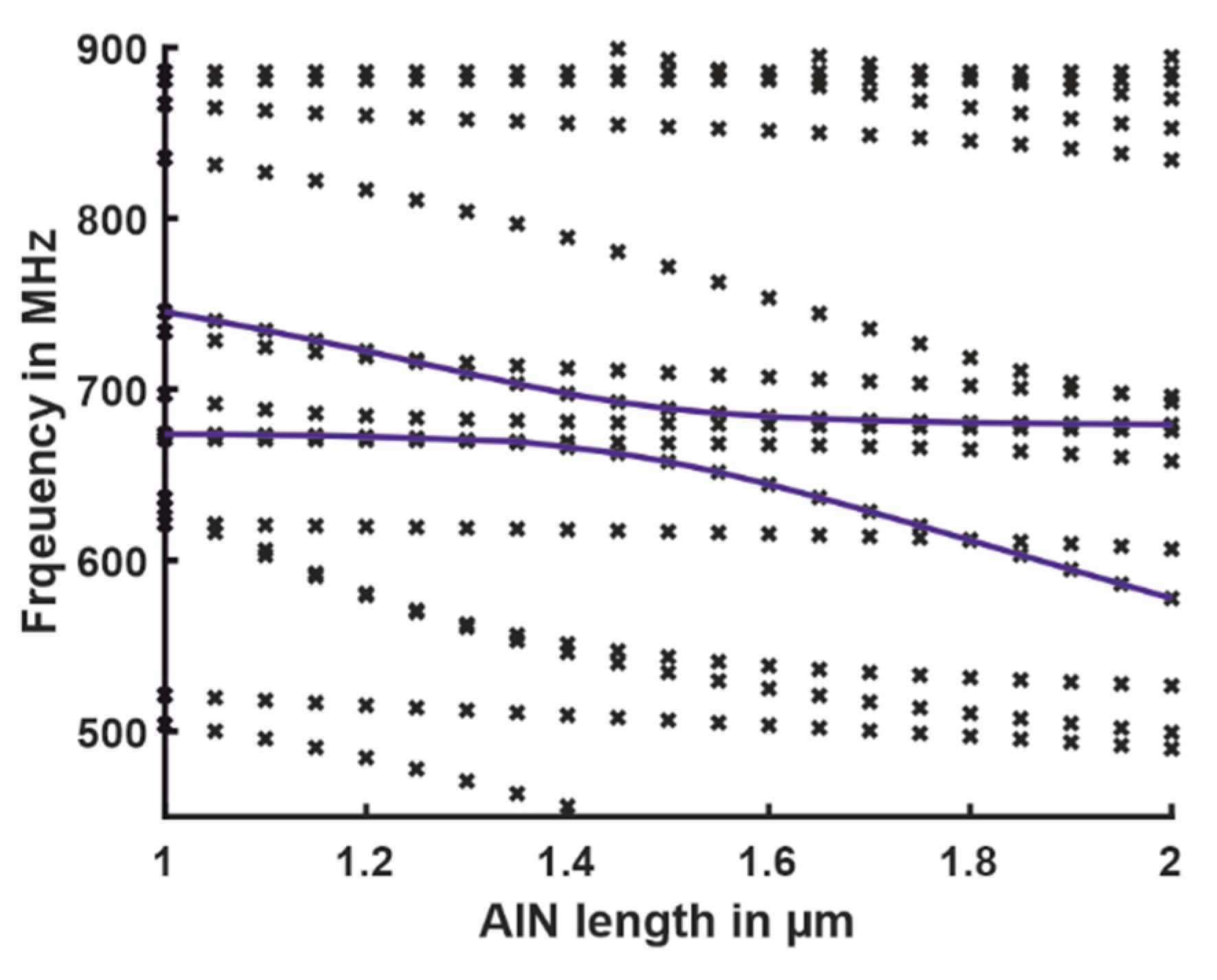
3.2. Device Design
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sauerbrey, G. Verwendung von Schwingquarzen zur Wägung dünner Schichten und zur Mikrowägung. Z. Physik 1959, 155, 206–222. [Google Scholar] [CrossRef]
- Alassi, A.; Benammar, M.; Brett, D. Quartz Crystal Microbalance Electronic Interfacing Systems: A Review. Sensors 2017, 17, 2799. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Knobel, R.G. Mass sensors: Weighing single atoms with a nanotube. Nat. Nanotechnol. 2008, 3, 525–526. [Google Scholar] [CrossRef] [PubMed]
- Ekinci, K.L. Electromechanical transducers at the nanoscale: Actuation and sensing of motion in nanoelectromechanical systems (NEMS). Small 2005, 1, 786–797. [Google Scholar] [CrossRef] [PubMed]
- Chaste, J.; Eichler, A.; Moser, J.; Ceballos, G.; Rurali, R.; Bachtold, A. A nanomechanical mass sensor with yoctogram resolution. Nat. Nanotechnol. 2012, 7, 301–304. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Arash, B. A review on applications of carbon nanotubes and graphenes as Nano-Resonator sensors. Comput. Mater. Sci. 2014, 82, 350–360. [Google Scholar] [CrossRef]
- Xu, D.; Wu, G.; Xiong, B.; Wang, Y. A resonant MEMS magnetic field sensor with electromagnetic induction sensing. In Proceedings of the 9th IEEE International Conference on Nano/Micro Engineered and Molecular Systems (NEMS), Waikiki Beach, HI, USA, 13–16 April 2014; IEEE: New York, NY, USA, 2014; Volume 42014, pp. 143–146, ISBN 978-1-4799-4726-3. [Google Scholar]
- Greywall, D.S.; Yurke, B.; Busch, P.A.; Pargellis, A.N.; Willett, R.L. Evading amplifier noise in nonlinear oscillators. Phys. Rev. Lett. 1994, 72, 2992–2995. [Google Scholar] [CrossRef]
- Lavrik, N.V.; Datskos, P.G. Femtogram mass detection using photothermally actuated nanomechanical resonators. Appl. Phys. Lett. 2003, 82, 2697–2699. [Google Scholar] [CrossRef]
- Ekinci, K.L.; Yang, Y.T.; Roukes, M.L. Ultimate limits to inertial mass sensing based upon nanoelectromechanical systems. J. Appl. Phys. 2004, 95, 2682–2689. [Google Scholar] [CrossRef] [Green Version]
- Ekinci, K.L.; Huang, X.M.H.; Roukes, M.L. Ultrasensitive nanoelectromechanical mass detection. Appl. Phys. Lett. 2004, 84, 4469–4471. [Google Scholar] [CrossRef] [Green Version]
- Jensen, K.; Kim, K.; Zettl, A. An Atomic-Resolution nanomechanical mass sensor. Nat. Nanotechnol. 2008, 3, 533–537. [Google Scholar] [CrossRef] [PubMed]
- Lassagne, B.; Garcia-Sanchez, D.; Aguasca, A.; Bachtold, A. Ultrasensitive mass sensing with a nanotube electromechanical resonator. Nano Lett. 2008, 8, 3735–3738. [Google Scholar] [CrossRef] [PubMed]
- Naik, A.K.; Hanay, M.S.; Hiebert, W.K.; Feng, X.L.; Roukes, M.L. Towards Single-Molecule nanomechanical mass spectrometry. Nat. Nanotechnol. 2009, 4, 445–450. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.; Bhaskaran, H. Ultrasensitive Room-Temperature piezoresistive transduction in Graphene-Based NanoelectromeChanical systems. Nano Lett. 2015, 15, 2562–2567. [Google Scholar] [CrossRef] [PubMed]
- Sage, E.; Sansa, M.; Fostner, S.; Defoort, M.; Gély, M.; Naik, A.K.; Morel, R.; Duraffourg, L.; Roukes, M.L.; Alava, T.; et al. Single-Particle mass spectrometry with arrays of Frequency-Addressed nanomechanical resonators. Nat. Commun. 2018, 9, 3283. [Google Scholar] [CrossRef] [Green Version]
- Chang, Y.; Bai, R.; Zhang, G.; Liu, Y.; Sun, K. Ultrasensitive Mass Sensing with a Nanomechanical Transistor. In Proceedings of the 2019 IEEE 19th International Conference on Communication Technology (ICCT), Xi’an, China, 16–19 October 2019; IEEE: New York, NY, USA, 2019; Volume 102019, pp. 1188–1192, ISBN 978-1-7281-0535-2. [Google Scholar]
- Toledo, J.; Ruiz-Díez, V.; Bertke, M.; Suryo Wasisto, H.; Peiner, E.; Sánchez-Rojas, J.L. Piezoelectric MEMS Resonators for CigaRette Particle Detection. Micromachines 2019, 10, 145. [Google Scholar] [CrossRef] [Green Version]
- Ekinci, K.L.; Roukes, M.L. Nanoelectromechanical systems. Rev. Sci. Instrum. 2005, 76, 61101. [Google Scholar] [CrossRef] [Green Version]
- Blencowe, M.P.; Wybourne, M.N. Sensitivity of a micromechanical displacement detector based on the Radio-Frequency Single-Electron transistor. Appl. Phys. Lett. 2000, 77, 3845–3847. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Zhang, Z.; Sang, L.; Li, T.; You, J.; Lu, Y.; Koide, Y.; Liao, M. Electrical readout/characterization of single crystal diamond (SCD) cantilever resonators. Diamond Related Mater. 2020, 103, 107711. [Google Scholar] [CrossRef]
- Pruessner, M.W.; Park, D.; Stievater, T.H.; Kozak, D.A.; Rabinovich, W.S. Cavity Optomechanical Photothermal Sensors. In Proceedings of the 2018 IEEE Photonics Conference (IPC), Reston, VA, USA, 30 September–4 October 2018; IEEE: New York, NY, USA, 2018; Volume 92018, pp. 1–2, ISBN 978-1-5386-5358-6. [Google Scholar]
- Arnau, A.; Sogorb, T.; Jiménez, Y. Circuit for continuous motional series resonant frequency and motional resistance monitoring of quartz crystal resonators by parallel capacitance compensation. Rev. Sci. Instrum. 2002, 73, 2724–2737. [Google Scholar] [CrossRef] [Green Version]
- Blevins, R.D. Formulas for Natural Frequency and Mode Shape; Krieger Publishing: Malabar, FL, USA, 2001; ISBN 1575241846. [Google Scholar]
- Firestone, F.A. A New Analogy Between Mechanical and Electrical Systems. J. Acoust. Soc. Am. 1933, 4, 249–267. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; He, L.; Wang, X.; Zhou, J.; Xu, W.; Smagin, N.; Toubal, M.; Yu, H.; Gu, Y.; Xu, J.; et al. 3D FEM Analysis of High-Frequency AlN-Based PMUT Arrays on Cavity SOI. Sensors 2019, 19, 4450. [Google Scholar] [CrossRef] [PubMed] [Green Version]
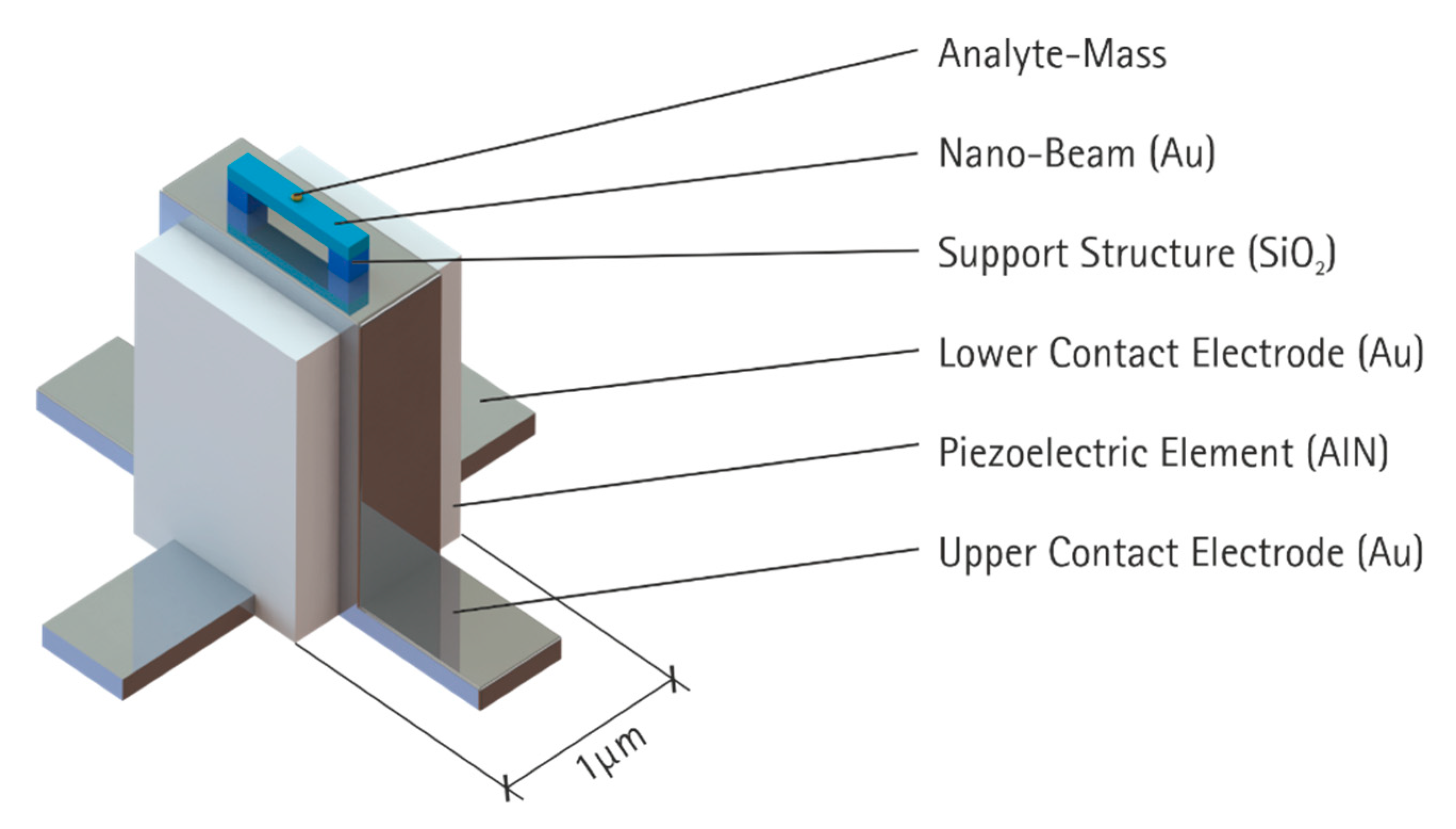



| Property | Unit | AlN | Au | SiO2 |
|---|---|---|---|---|
| Density | kg/m3 | 3512 | 19320 | 2200 |
| Poisson ratio | - | 0.3 | 0.42 | 0.17 |
| Stiffness coefficient c11 | GPa | 345 | ||
| Stiffness coefficient c12 | GPa | 125 | ||
| Stiffness coefficient c13 | GPa | 120 | ||
| Stiffness coefficient c33 /Elastic modulus | GPa | 395 | 79 | 70 |
| Stiffness coefficient c44 | GPa | 118 | ||
| Stiffness coefficient c66 | GPa | 110 | ||
| Piezoelectric constant e31 | C/m2 | −0.58 | ||
| Piezoelectric constant e33 | C/m2 | 1.55 | ||
| Piezoelectric constant e15 | C/m2 | −0.48 | ||
| Relative permittivity ε/ε0 | - | 11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Twiefel, J.; Glukhovkoy, A.; de Wall, S.; Wurz, M.C.; Sehlmeyer, M.; Hitzemann, M.; Zimmermann, S. Towards a Highly Sensitive Piezoelectric Nano-Mass Detection—A Model-Based Concept Study. Sensors 2021, 21, 2533. https://doi.org/10.3390/s21072533
Twiefel J, Glukhovkoy A, de Wall S, Wurz MC, Sehlmeyer M, Hitzemann M, Zimmermann S. Towards a Highly Sensitive Piezoelectric Nano-Mass Detection—A Model-Based Concept Study. Sensors. 2021; 21(7):2533. https://doi.org/10.3390/s21072533
Chicago/Turabian StyleTwiefel, Jens, Anatoly Glukhovkoy, Sascha de Wall, Marc Christopher Wurz, Merle Sehlmeyer, Moritz Hitzemann, and Stefan Zimmermann. 2021. "Towards a Highly Sensitive Piezoelectric Nano-Mass Detection—A Model-Based Concept Study" Sensors 21, no. 7: 2533. https://doi.org/10.3390/s21072533






