Optimal Implementation Parameters of a Nonlinear Electrical Impedance Tomography Method Using the Complete Electrode Model
Abstract
:1. Introduction
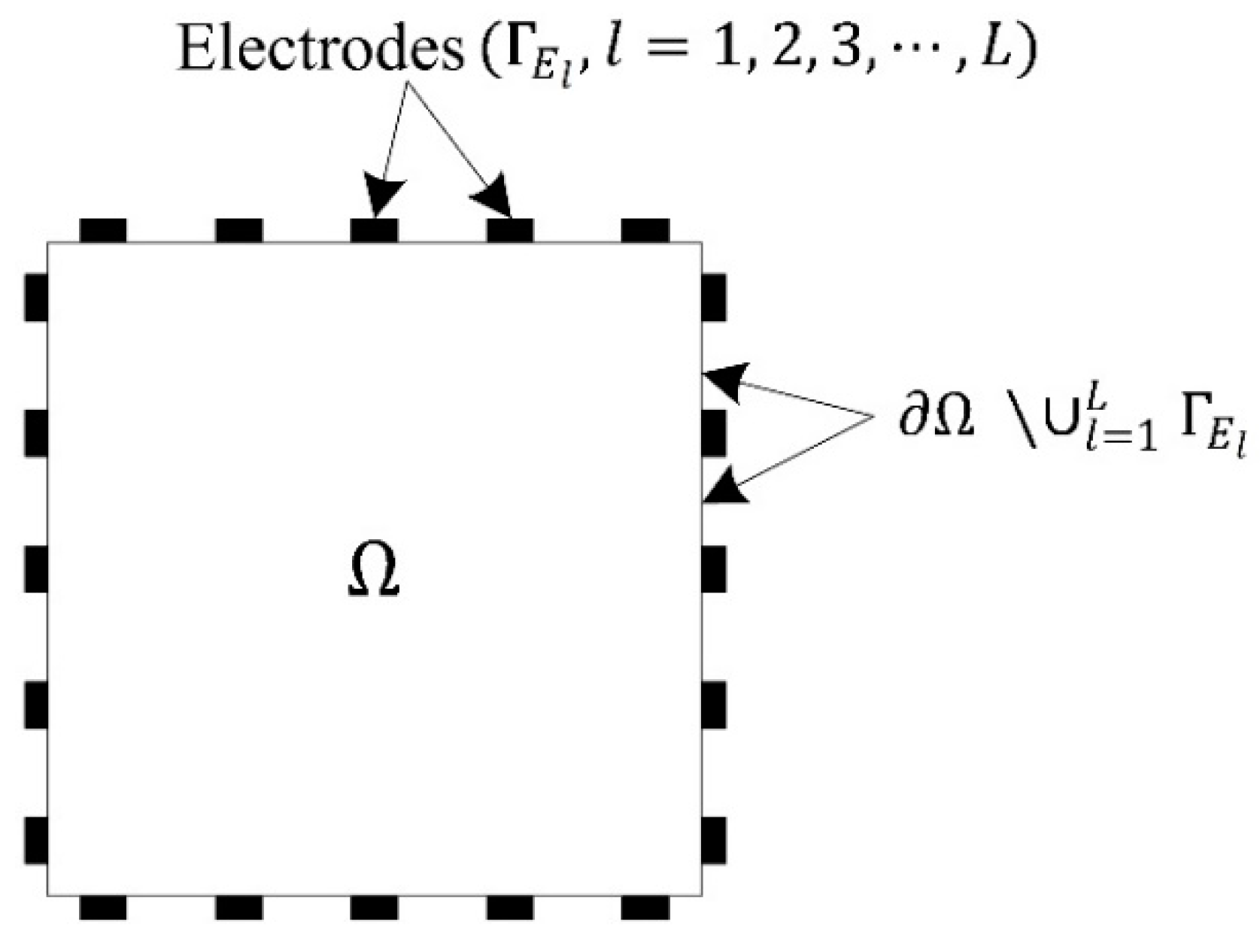
2. The Forward Problem
2.1. Mathematical Method
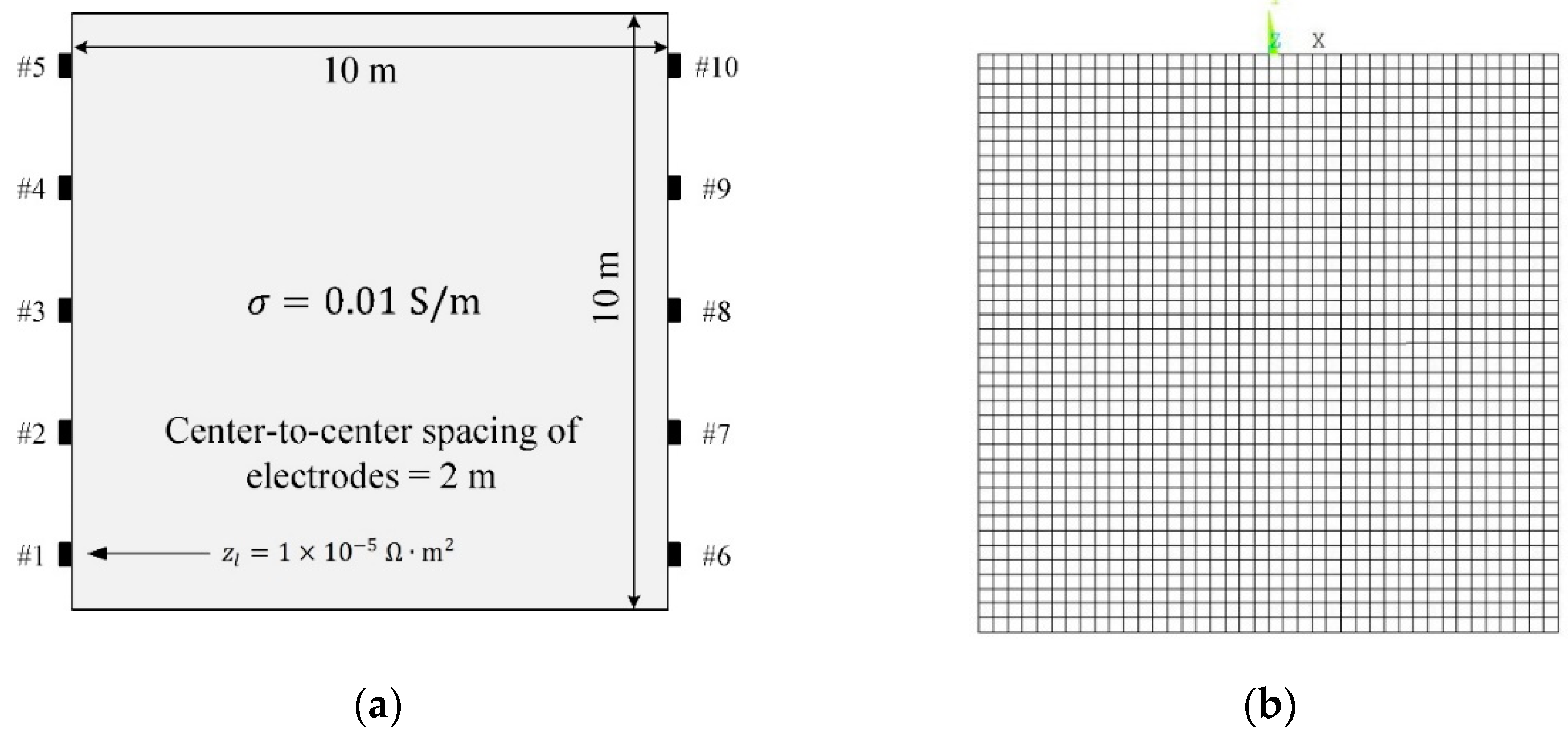
2.2. Setting for Numerical Analysis
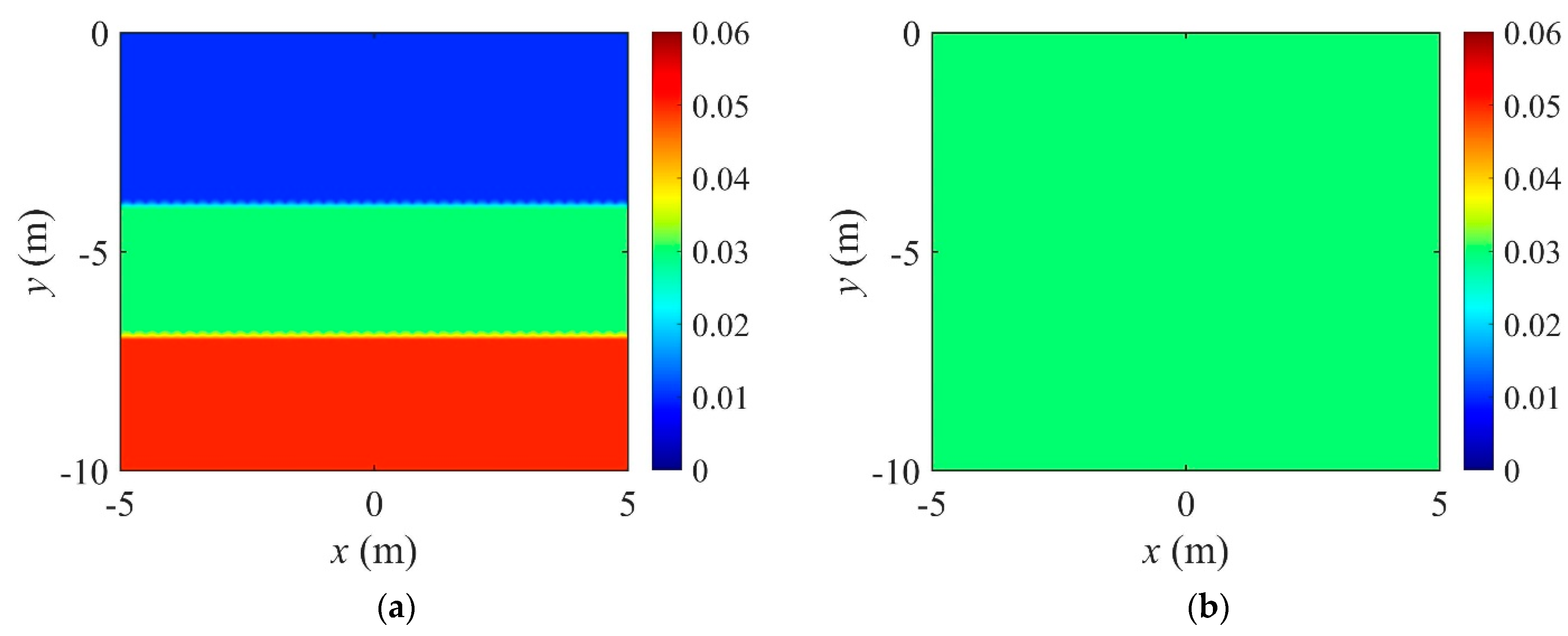
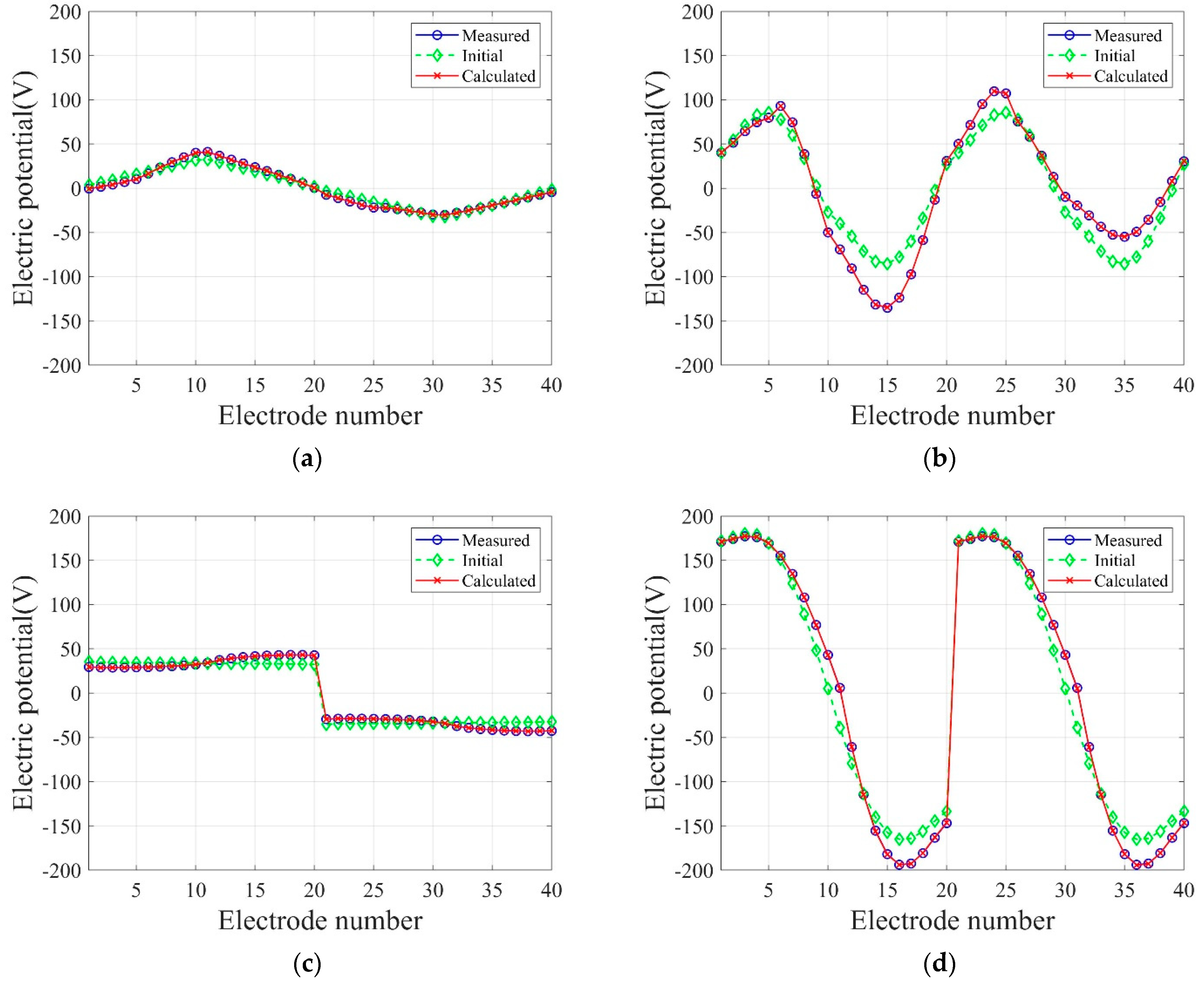
2.3. Results of the Validation
3. The Inverse Problem
3.1. PDE-Constrained Optimization
3.2. Regularization Schemes
3.3. First-Order Optimality Conditions
3.3.1. First Optimality Condition: State Problem
3.3.2. Second Optimality Condition: Adjoint Problem
3.3.3. Third Optimality Condition: Control Problem
3.4. Material Property Update
- Assume the initial electrical conductivity profile of a structure to be investigated, then calculate the electric potential and due to the current input through the surface electrodes.
- Calculate the adjoint solutions and using the state solution .
- Using the state and adjoint solutions, calculate the gradient of the Lagrangian with respect to the control variable , as follows:In Equation (20), the TN regularization scheme was used. If the TV scheme were assumed, then the Lagrangian gradient for would be
- Update the electrical conductivity at each node using a line search method. Equations (17) and (18) are not precisely enforced in updating the electrical conductivity at boundaries since they are complicated to implement. Instead, one can enforce that the normal derivative of be zero along the boundary for computational simplicity.
3.5. Conjugate Gradient Method with an Inexact Line Search
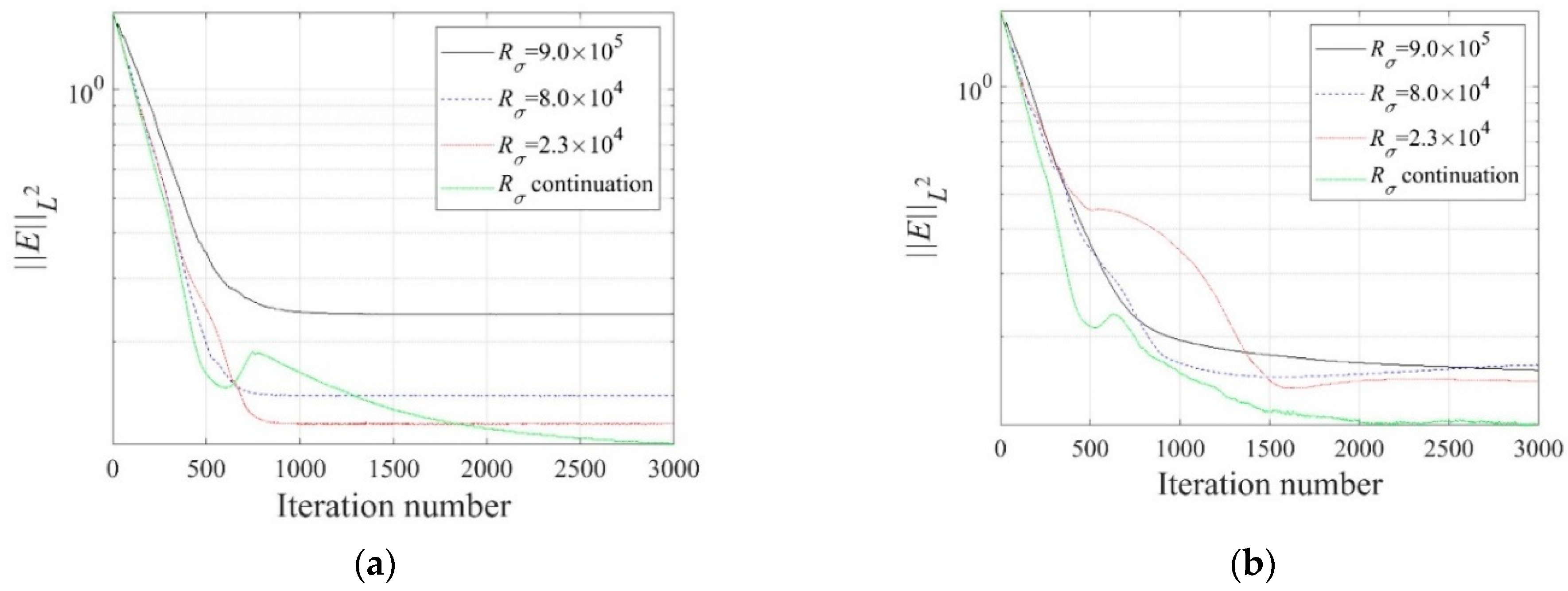
3.6. Regularization Factor Continuation Scheme
4. Numerical Studies for Optimal EIT Parameters
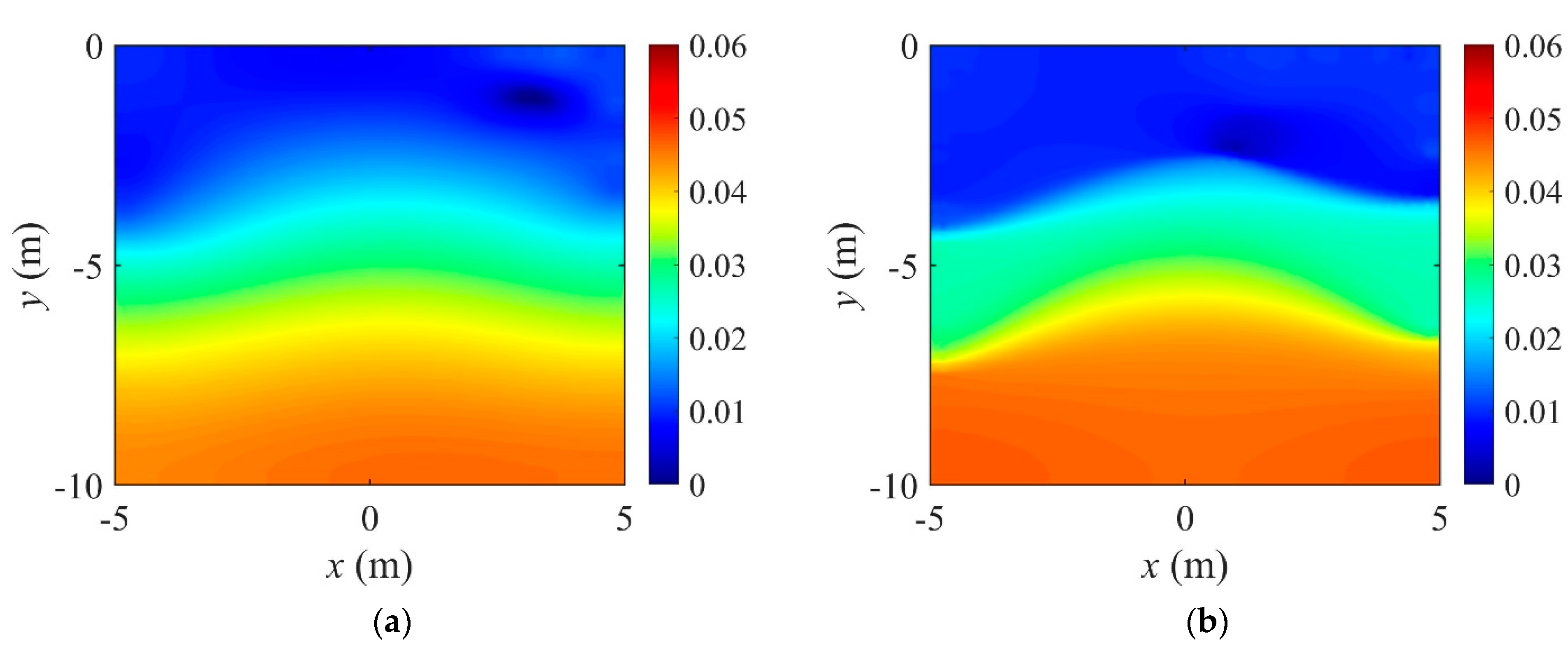
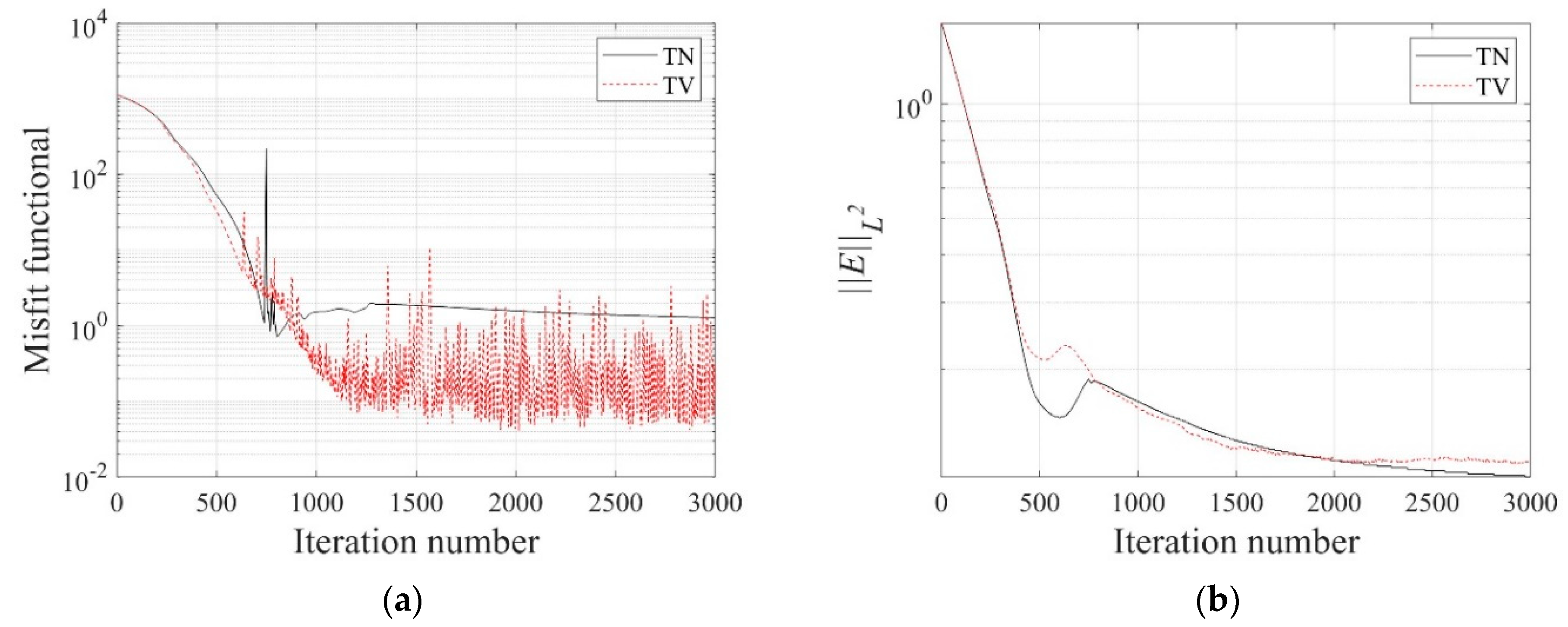
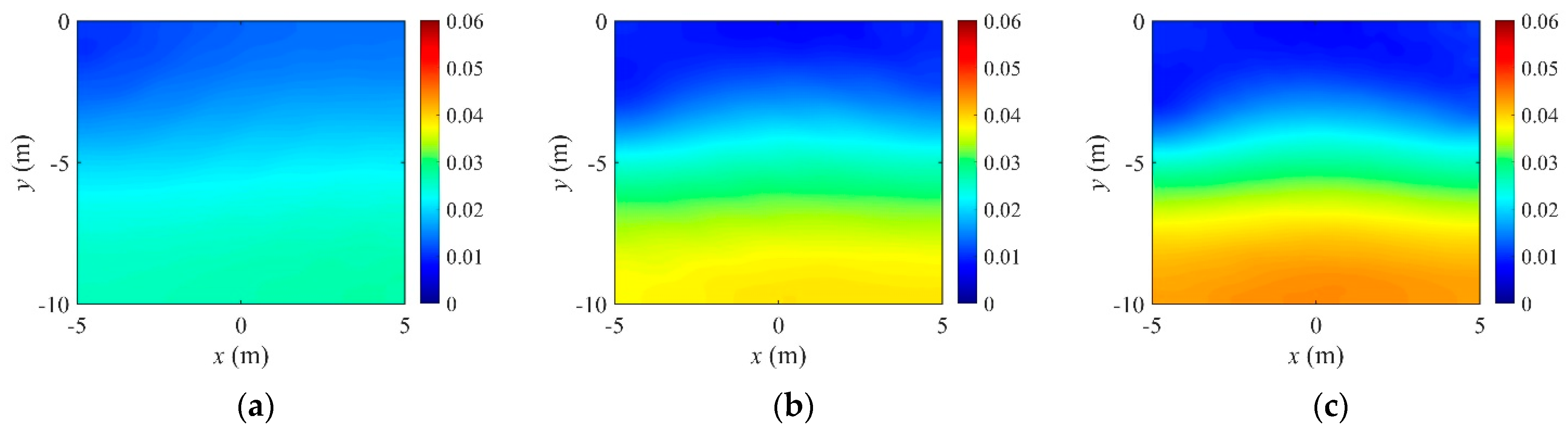
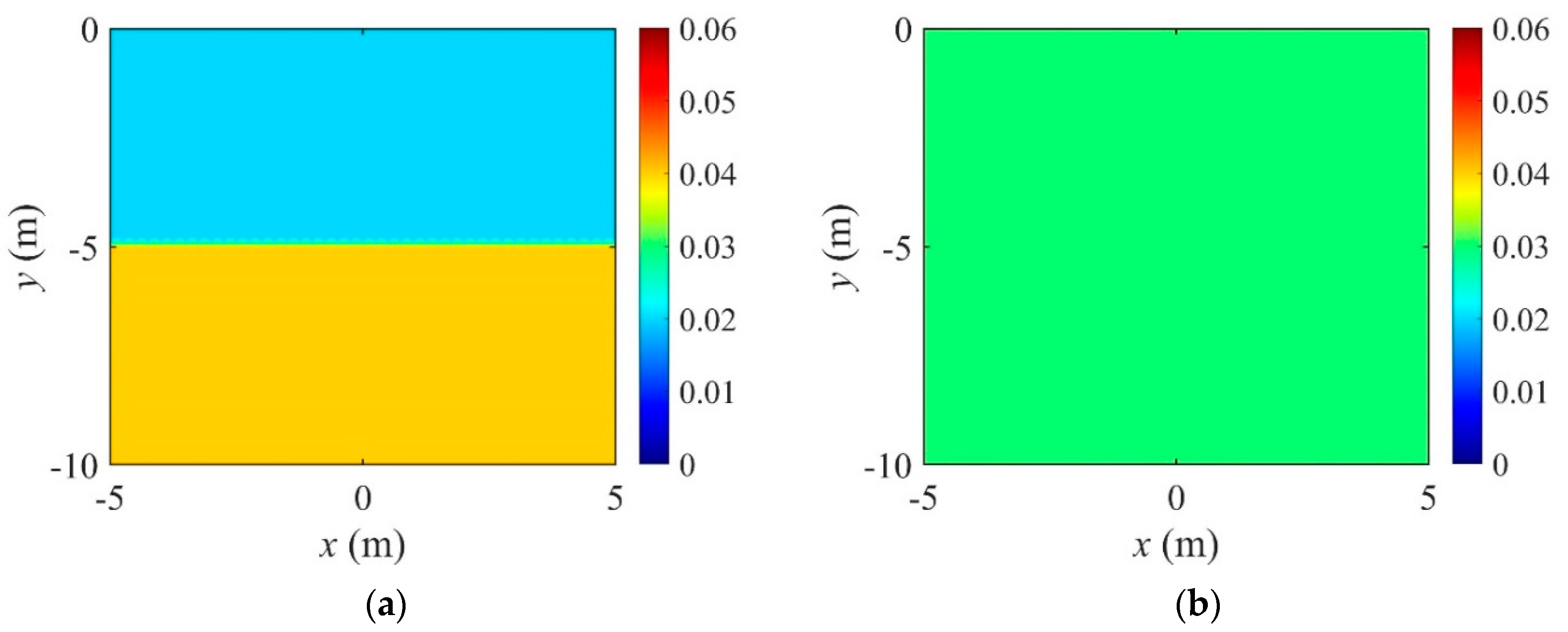
4.1. Regularization Effect
4.2. Parametric Studies for Optimal EIT Result
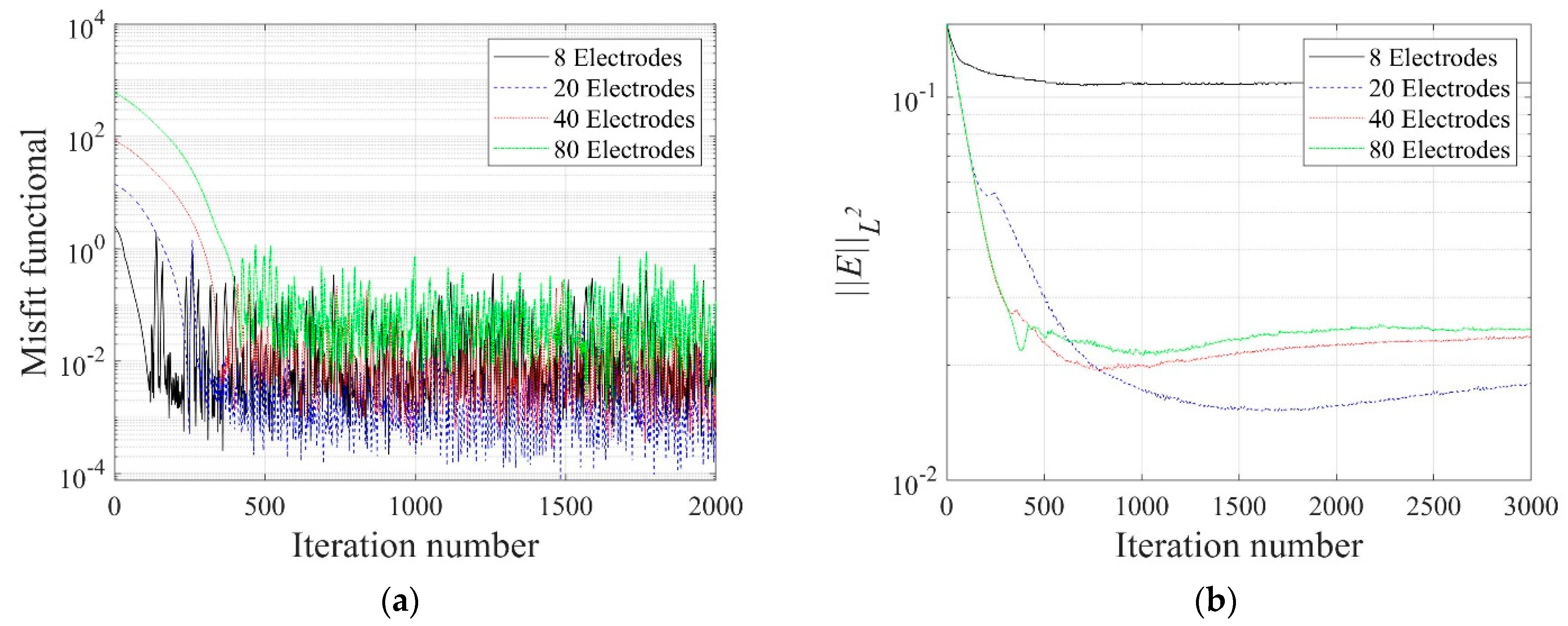
4.2.1. Number of Electrodes
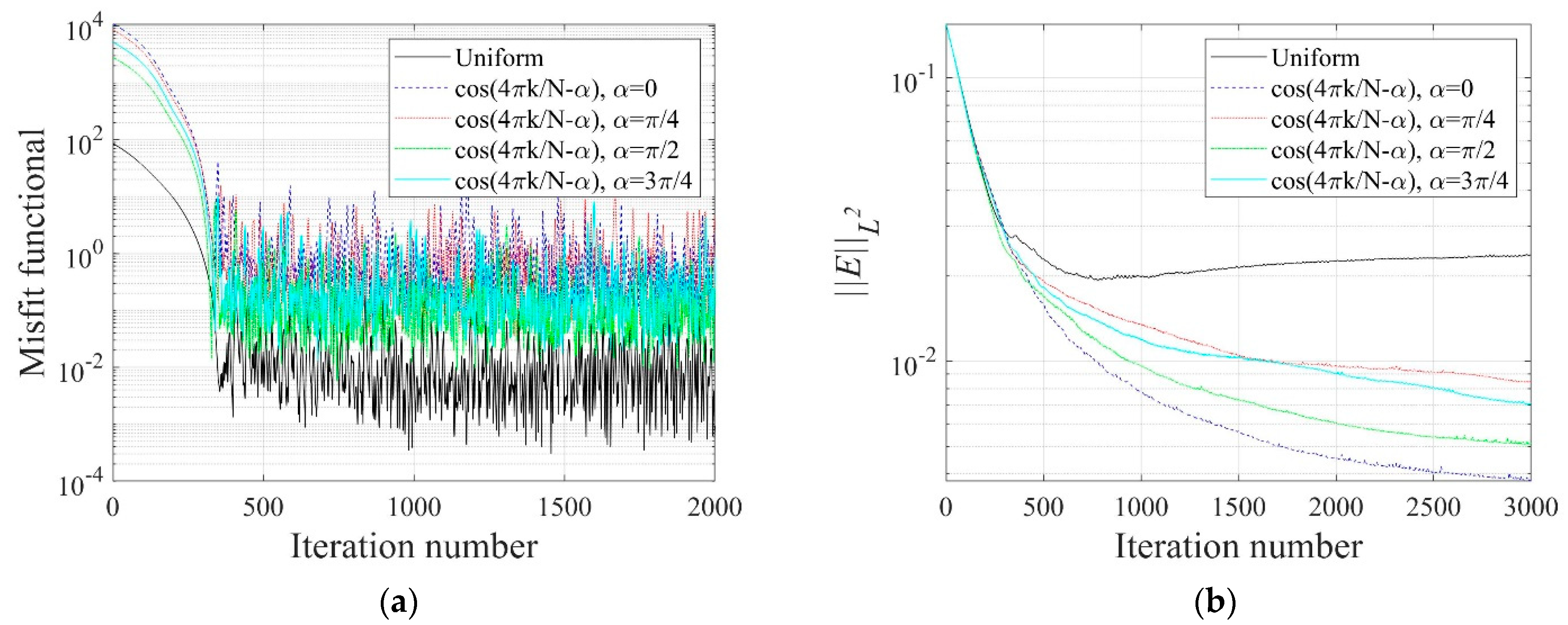
4.2.2. Current Input Pattern
4.2.3. Electrode Arrangement
4.3. Optimal Choice of Implementation Parameters
5. Conclusions
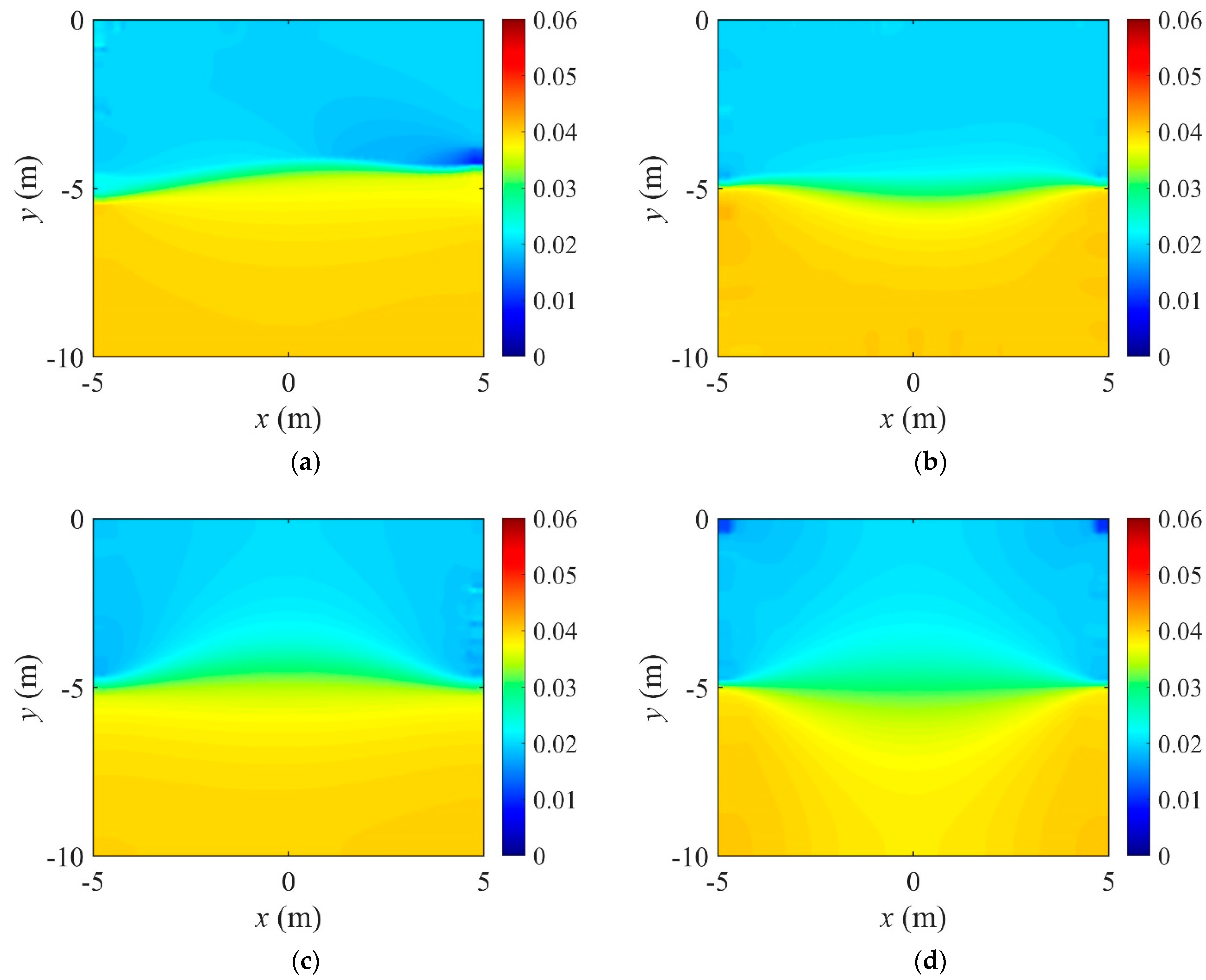
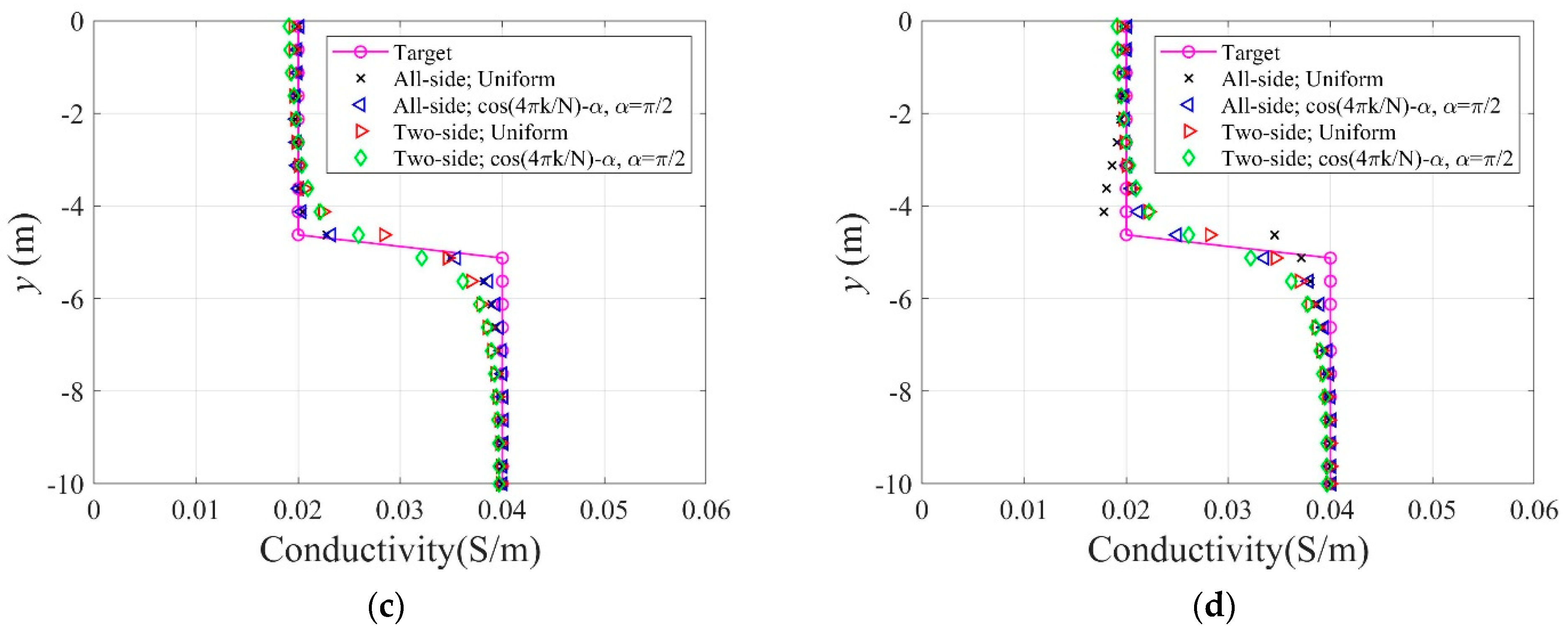
- The layered profile was reconstructed more clearly when using the TV regularization scheme than TN, especially at the interface of layers. The inversion result was improved when using the regularization factor continuation scheme rather than the fixed method.
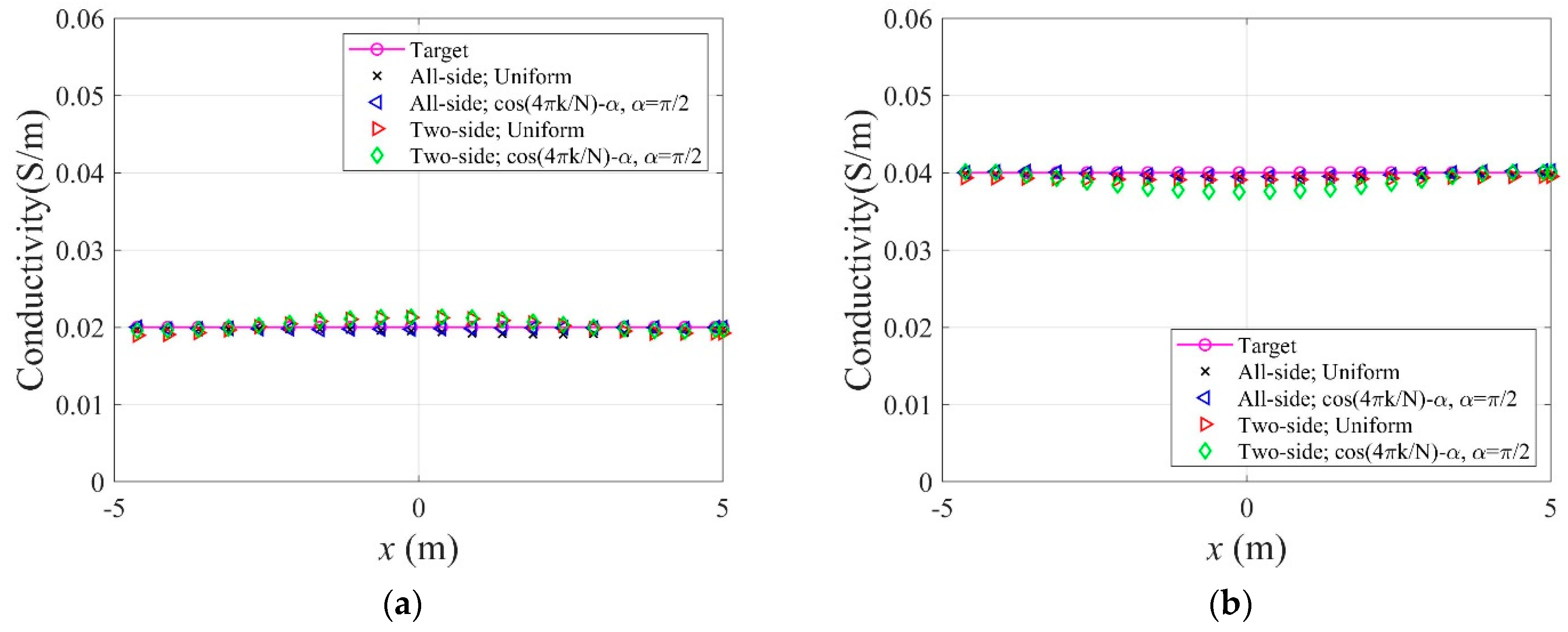
- A higher number of electrodes did not necessarily improve the inversion results. In addition, the TN regularization scheme produced relevant results when the number of electrodes was small.
- The layered profiles were successfully reconstructed for all the presented current patterns. The relative -error was smaller when the cosine pattern was used, especially when the phase or .
- In the case of arranging electrodes on all sides of the square domain, the inversion result was improved compared to the case of arranging them only on two sides.
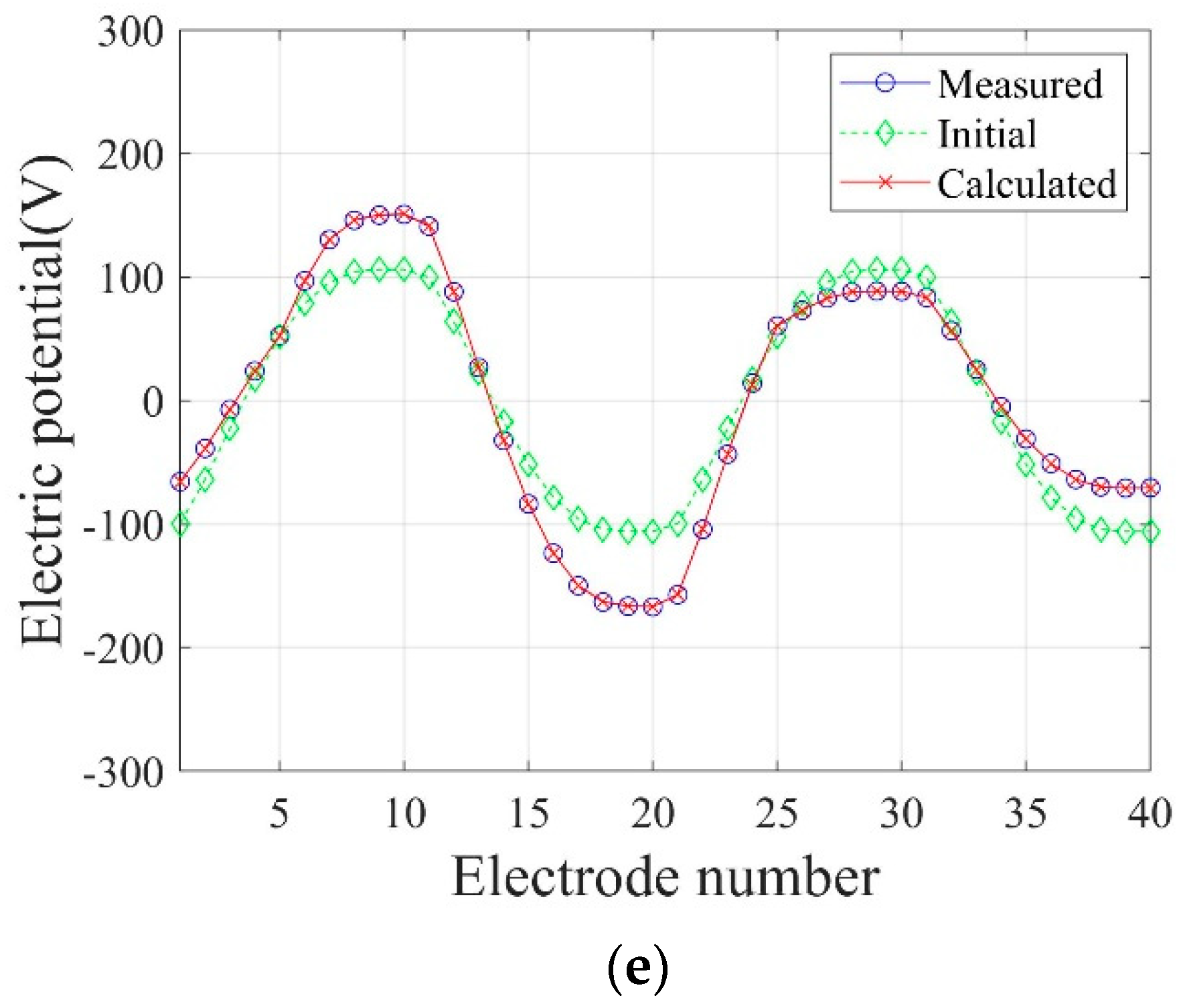
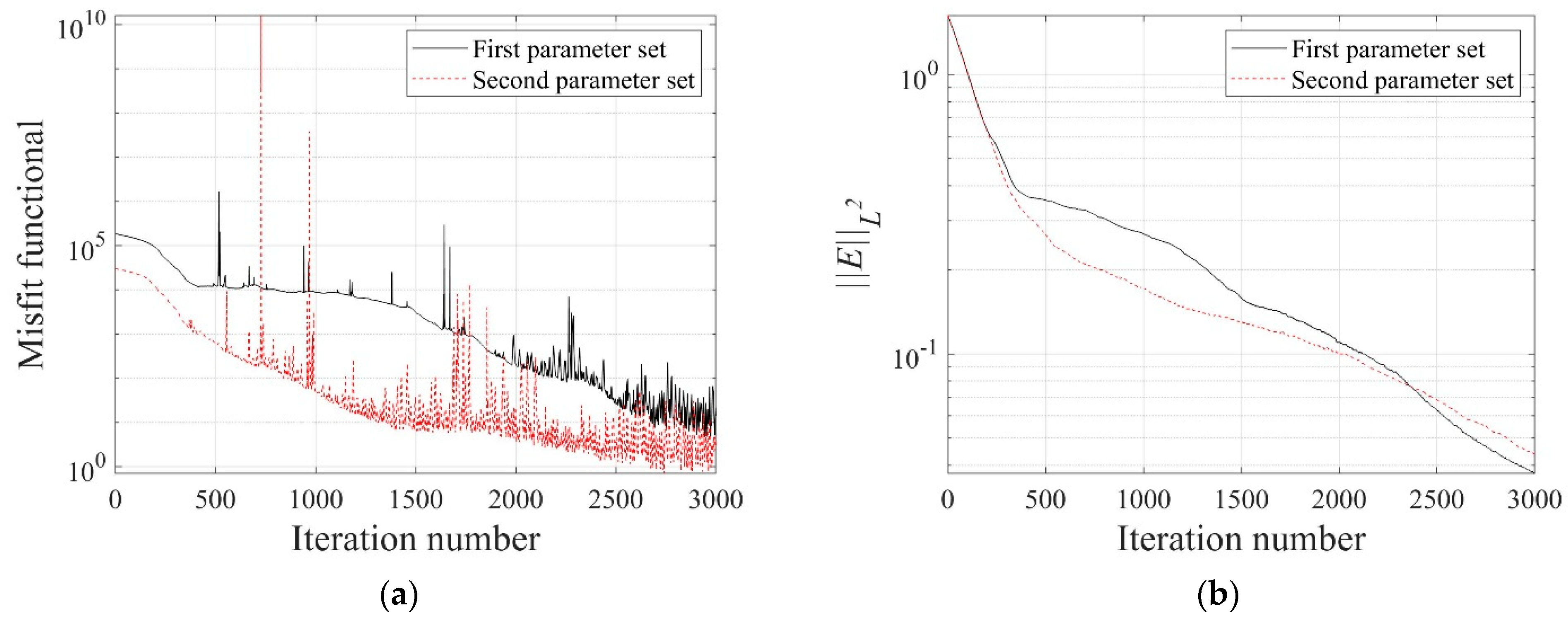
- The relative -error and the relative misfit are proper criteria for optimal implementation parameters. The relative -error was decreased by 95.1% from the initial value when using the first set of optimal parameters. It was also reduced by 94.4% when using the second set. The presented optimal parameter sets worked successfully in reconstructing layered electrical conductivity profiles.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Alphabetic symbols | |
| Area of square domain | |
| Search direction vector | |
| th electrode | |
| th electrode | |
| Force vector | |
| th inversion iteration | |
| Hessian matrix | |
| th electrode | |
| Current density | |
| Stiffness matrix | |
| Number of electrodes | |
| Number of nodes in finite element mesh | |
| Basis vector | |
| Regularization factor | |
| Vector consisting of electric potential at each electrode | |
| th electrode | |
| th electrode | |
| Solution vector | |
| Electric potential in domain | |
| Test value | |
| Test function | |
| Lagrange multiplier | |
| Lagrange multiplier | |
| th electrode | |
| Greek symbols | |
| Step length | |
| Initial step length | |
| Small parameter for TV regularization scheme | |
| th electrode | |
| Small parameter for Armijo condition | |
| Parameter for reducing step length | |
| Electrical conductivity | |
| Legendre basis function | |
| Structural domain | |
References
- Hamilton, S.J.; Hauptmann, A. Deep D-bar: Real-time electrical impedance tomography imaging with deep neural networks. IEEE Trans. Med. Imaging 2018, 37, 2367–2377. [Google Scholar] [CrossRef] [PubMed]
- Abdulla, U.G.; Bukshtynov, V.; Seif, S. Cancer detection through Electrical Impedance Tomography and optimal control theory: Theoretical and computational analysis. Math. Biosci. Eng. 2021, 18, 4834–4859. [Google Scholar] [CrossRef] [PubMed]
- Yenjaichon, W.; Grace, J.R.; Lim, C.J.; Bennington, C.P.J. In-line jet mixing of liquid–pulp–fibre suspensions: Effect of concentration and velocities. Chem. Eng. Sci. 2012, 75, 167–176. [Google Scholar] [CrossRef]
- Yenjaichon, W.; Grace, J.R.; Lim, C.J.; Bennington, C.P.J. Characterisation of gas mixing in water and pulp-suspension flow based on electrical resistance tomography. Chem. Eng. J. 2013, 214, 285–297. [Google Scholar] [CrossRef]
- Stevenson, R.; Harrison, S.T.L.; Miles, M.; Cilliers, J.J. Examination of swirling flow using electrical resistance tomography. Powder Technol. 2006, 162, 157–165. [Google Scholar] [CrossRef]
- Giguere, R.; Fradette, L.; Mignon, D.; Tanguy, P.A. Characterisation of slurry flow regime transitions by ERT. Chem. Eng. Res. Des. 2008, 86, 989–996. [Google Scholar] [CrossRef]
- Cheng, Q.; Tao, M.; Chen, X.; Binley, A. Evaluation of electrical resistivity tomography (ERT) for mapping the soil–rock interface in karstic environments. Environ. Earth Sci. 2019, 78, 439. [Google Scholar] [CrossRef]
- Jordana, J.; Gasulla, M.; Pallas-Areny., R. Electrical resistance tomography to detect leaks from buried pipes. Meas. Sci. Technol. 2001, 12, 1061–1068. [Google Scholar] [CrossRef]
- Ts, M.-E.; Lee, E.; Zhou, L.; Lee, K.H.; Seo, J.K. Remote real time monitoring for underground contamination in Mongolia using electrical impedance tomography. J. Nondestruct. Eval. 2006, 35, 8. [Google Scholar] [CrossRef]
- Kauppinen, P.; Hyttinen, J.; Malmivuo, J. Sensitivity distribution visualization of impedance tomography measurement strategies. Int. J. Bioelectromagn. 2016, 8, 63–71. [Google Scholar]
- Graham, B.H.; Adler, A. Electrode placement configuration for 3D EIT. Physiol. Meas. 2007, 28, S29–S44. [Google Scholar] [CrossRef] [PubMed]
- Schullcke, B.; Krueger-Ziolek, S.; Gong, B.; Moeller, K. Effect of the number of electrodes on the reconstructed lung shape in electrical impedance tomography. Curr. Dir. Biomed. Eng. 2006, 2, 499–502. [Google Scholar] [CrossRef]
- Brown, B.H.; Seagar, A.D. The Sheffield data collection system. Clin. Phys. Physiol. Meas. 1987, 8, 91–97. [Google Scholar] [CrossRef] [PubMed]
- Avis, N.J.; Barber, D.C. Image reconstruction using non-adjacent drive configurations. Physiol. Meas. 1994, 15, A153–A160. [Google Scholar] [CrossRef]
- Gisser, D.G.; Isaacson, D.; Newell, J.C. Current topics in impedance imaging. Clin. Phys. Physiol. Meas. 1987, 8, 39–46. [Google Scholar] [CrossRef]
- Harikumar, R.; Prabu, R.; Raghavan, S. Electrical impedance tomography (EIT) and its medical applications: A review. Int. J. Soft Comput. Eng. 2013, 3, 193–198. [Google Scholar]
- Dobson, D.C.; Santosa, F. Resolution and stability of an inverse problem in electrical impedance tomography: Dependence on the input current patterns. SIAM J. Appl. Math. 1994, 54, 1542–1560. [Google Scholar] [CrossRef]
- Kolehmainen, V.; Vauhkonen, M.; Karjalainen, P.A.; Kaipio, J.P. Assessment of errors in static electrical impedance tomography with adjacent and trigonometric current patterns. Physiol. Meas. 1997, 18, 289–303. [Google Scholar] [CrossRef]
- Jung, B.-G.; Kim, B.; Kang, J.W.; Hwang, J.-H. Electrode impedance tomography for material profile reconstruction of concrete structures. J. Comput. Struct. Eng. Inst. Korea 2019, 32, 249–256. [Google Scholar] [CrossRef]
- Jung, B.-G. Material Profile Reconstruction Using an Electrical Impedance Tomography Method Based on a Complete Electrode Model. Master’s Thesis, Hongik University, Seoul, Korea, 2019. [Google Scholar]
- ANSYS. Mechanical APDL Element References; ANSYS, Inc.: Canonsburg, PA, USA, 2016. [Google Scholar]
- Vauhkonen, P.J.; Vauhkonen, M.; Savolainen, T.; Kaipio, J.P. Three-dimensional electrical impedance tomography based on the complete electrode model. IEEE Trans. Biomed. Eng. 1999, 46, 1150–1160. [Google Scholar] [CrossRef]
- Cheng, K.; Isaacson, D.; Newell, J.C.; Gisser, D.G. Electrode models for electric current computed tomography. IEEE Trans. Biomed. Eng. 1989, 36, 918–924. [Google Scholar] [CrossRef] [PubMed]
- Somersalo, E.; Cheney, M.; Isaacson, D. Existence and uniqueness for electrode models for electric current computed tomography. SIAM J. Appl. Math. 1992, 52, 1023–1040. [Google Scholar] [CrossRef]
- Tikhonov, A.N. Solution of Incorrectly Formulated Problems and the Regularization Method. Sov. Math. Dokl. 1963, 4, 1035–1038. [Google Scholar]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Pakravan, A.; Kang, J.W. A Gauss-Newton Full-waveform Inversion for Material Profile Reconstruction in 1D PML-truncated Solid Media. KSCE J. Civ. Eng. 2014, 18, 1792–1804. [Google Scholar] [CrossRef]
- Pakravan, A.; Kang, J.W.; Newtson, C.M. A Gauss–Newton full-waveform inversion for material profile reconstruction in viscoelastic semi-infinite solid media. Inverse Probl. Sci. Eng. 2016, 24, 393–421. [Google Scholar] [CrossRef]
- Pakravan, A.; Kang, J.W.; Newtson, C.M. A Gauss–Newton full-waveform inversion in PML-truncated domains using scalar probing waves. J. Comput. Phys. 2017, 350, 824–846. [Google Scholar] [CrossRef]
- Kang, J.W.; Kallivokas, L.F. The inverse medium problem in 1D PML-truncated heterogeneous semi-infinite domains. Inverse Probl. Sci. Eng. 2010, 18, 759–786. [Google Scholar] [CrossRef]
- Kang, J.W.; Kallivokas, L.F. The inverse medium problem in heterogeneous PML-truncated domains using scalar probing waves. Comput. Methods Appl. Mech. Eng. 2011, 200, 265–283. [Google Scholar] [CrossRef]
- Joh, N.; Kang, J.W. Material profile reconstructing using plane electromagnetic waves in PML-truncated heterogeneous domains. Appl. Math. Modeling 2021, 96, 813–833. [Google Scholar] [CrossRef]
- Neville, A.M. Properties of Concrete; Longman: London, UK, 1995. [Google Scholar]



















| Choose , , set repeat until Terminate with |
| Current Input Pattern | Electrode Arrangement | |||||||
|---|---|---|---|---|---|---|---|---|
| All-Side Arrangement | Two-Side Arrangement | |||||||
| Number of Electrodes | Number of Electrodes | |||||||
| 8 | 20 | 40 | 80 | 8 | 20 | 40 | 80 | |
| Uniform | ||||||||
| Cosine, | ||||||||
| Cosine, | ||||||||
| Cosine, | ||||||||
| Cosine, | ||||||||
| Current Input Pattern | Electrode Arrangement | |||||||
|---|---|---|---|---|---|---|---|---|
| All-Side Arrangement | Two-Side Arrangement | |||||||
| Number of Electrodes | Number of Electrodes | |||||||
| 8 | 20 | 40 | 80 | 8 | 20 | 40 | 80 | |
| Uniform | ||||||||
| Cosine, | ||||||||
| Cosine, | ||||||||
| Cosine, | ||||||||
| Cosine, | ||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Kang, J.W.; Choi, E. Optimal Implementation Parameters of a Nonlinear Electrical Impedance Tomography Method Using the Complete Electrode Model. Sensors 2022, 22, 6667. https://doi.org/10.3390/s22176667
Park J, Kang JW, Choi E. Optimal Implementation Parameters of a Nonlinear Electrical Impedance Tomography Method Using the Complete Electrode Model. Sensors. 2022; 22(17):6667. https://doi.org/10.3390/s22176667
Chicago/Turabian StylePark, Jeongwoo, Jun Won Kang, and Eunsoo Choi. 2022. "Optimal Implementation Parameters of a Nonlinear Electrical Impedance Tomography Method Using the Complete Electrode Model" Sensors 22, no. 17: 6667. https://doi.org/10.3390/s22176667





